简支梁桥上板式无砟轨道钢轨纵向力分析★

郑 祯 国

(中国铁路南昌局集团有限公司福州工务段，福建 福州 350013)

随着高速铁路的快速发展，人们对桥上无缝线路需求量大大增加；其中桥上板式无砟轨道结构形式以其使用寿命长、养护维修量小、稳定性好等特点在我国得到广泛应用。桥上无砟轨道无缝线路不同于一般铺设在路基上的无缝线路，桥梁结构因温度变化和列车荷载作用而发生伸缩和挠曲变形，使得桥上无缝线路除受来自车轮的轮轨力外，还将受到梁伸缩变形引起的附加伸缩力和挠曲变形引起的附加挠曲力。

国内外学者对桥上无缝线路纵向力的测定与计算进行了一些理论与试验研究[1-6]。孔文斌、雷晓燕[7]使用有限元法计算了高速铁路长大桥梁无砟轨道无缝线路附加挠曲力及附加挠曲位移，并分析了其分布规律；戴公连等[8]研究了30 t轴重重载铁路简支梁桥上无缝线路在温度和活载作用下的纵向力分布规律；张鹏飞、桂昊等[9]计算了列车荷载作用下简支梁桥CRTSⅠ型板式轨道结构的挠曲力与位移，并对相关参数进行了优化；陈扬、李成辉[10]等计算并分析了列车荷载作用下简支梁桥上CRTSⅠ型板式无砟轨道轨道板的纵向力与位移；江海波、吴迅[11]等在计算了桥梁和钢轨的相互作用力的基础上，建立了城市轨道交通桥梁无缝线路纵向力的空间一体化力学模型，并探究了双线桥梁上的单线荷载作用下的挠曲力、制动力的分布规律。桥上板式无砟轨道附加伸缩力、附加挠曲力及制动力作为梁轨相互作用原理中计算荷载的一部分，也是桥上无缝线路附加力中不可或缺的重要组成部分。因此，随着我国高速铁路发展力度的不断加大，对桥上板式无砟轨道无缝线路纵向力分析的相关研究显得尤为重要。

本文基于梁轨相互作用原理，运用有限元法建立了5跨简支梁桥板式无砟轨道线—板—桥—墩空间整体刚臂模型，该模型充分考虑了轨道结构、梁体、墩台的整体性，力求更好的反映出梁轨间的实际受力情况。计算在梁体温度荷载、列车荷载及制动荷载作用下的钢轨附加伸缩力、挠曲力、制动力与纵向位移。其研究结果可供桥上板式无砟轨道的设计及运营安全参考。

1 有限元模型与基本参数

1.1 计算假定

1)不考虑附加伸缩力、附加挠曲力、制动力及钢轨纵向位移之间的相互叠加作用。

2)假定固定支座能完全阻止梁产生的位移，对活动支座的摩阻力不予考虑。

3)将固定支座墩台顶纵向水平线刚度考虑为线性的。

1.2 计算模型及参数

本文结合简支梁桥上板式无砟轨道实际情况，建立了线—板—桥—墩的双线简支梁桥刚臂空间整体有限元模型。钢轨、墩台和梁体均采用梁单元模拟；扣件纵向阻力采用非线性弹簧单元模拟；扣件横、垂向刚度和固定支座墩台顶纵向刚度用线性弹簧单元模拟；在两侧路基末端对钢轨进行约束。

1)采用CHN60标准钢轨，全桥共5跨，每跨32 m，按实际扣件间距0.64 m划分单元，在表面每一扣件位置处均分别建立三个弹簧单元，其分别是采用弹簧—阻尼器单元模拟扣件横、垂向刚度和采用非线性弹簧单元来模拟扣件的纵向阻力。针对无砟轨道与桥梁间的摩阻力大于扣件阻力的特点，线路阻力取为扣件阻力，桥上无缝线路采用小阻力扣件纵向阻力模型，有载下扣件阻力取10 kN/(m·轨)，无载下扣件阻力取6.5 kN/(m·轨)，桥梁两侧路基段采用常阻力扣件，取15 kN/(m·轨)。

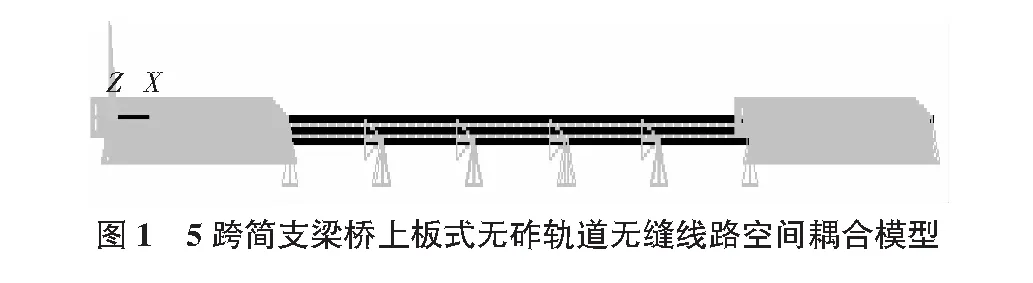
2)5跨简支梁桥上板式无砟轨道无缝线路空间耦合模型如图1所示，模型两端分别建了64 m的路基段对无缝线路进行约束。模型总共有节点数455个，刚臂单元数255个。

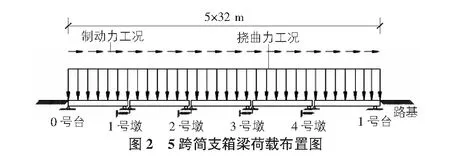
3)5跨简支梁桥荷载布置图如图2所示，其中制动力工况下采用ZK活载进行计算，施加在钢轨顶面上的制动力采用0.8UIC荷载的竖向均布荷载改为从左向右的纵向均布加载(64 kN/m)乘以制动力率0.10计算，即6.4 kN/m方向从左向右；挠曲力工况下采用对单线全桥均布加载的方式，荷载按ZK标准活载中的均布荷载进行加载。本文中钢轨纵向力图及位移图中的横坐标钢轨坐标均代表钢轨离0号台的距离，下同。

2 温度荷载下附加伸缩力计算及变形分析

本节在计算时，荷载工况仅考虑梁体升温情况，Δt取为20 ℃。

2.1 附加伸缩力计算结果分析

钢轨附加伸缩力如图3所示，图中正值表示拉力、负值表示压力(下同)；在各墩/台顶的计算结果如表1所示。

表1 各墩/台顶钢轨附加伸缩力 kN

由图3及表1可知，根据温度荷载的对称性，双线4股钢轨附加伸缩力都相同，所以取其中一股钢轨的附加伸缩力分析可得：附加伸缩力随桥墩号的增加而逐渐增大，且桥梁两端的桥台处最大，桥梁中部最小。

2.2 钢轨纵向位移计算结果分析

钢轨纵向位移如图4所示，其中正值表示拉伸变形、负值表示压缩变形(下同)；在各墩/台顶的计算结果如表2所示。

表2 各墩/台顶钢轨纵向位移(一) mm

由图4及表2可知，钢轨纵向位移呈先增后减的趋势，并在两侧路基段逐渐减小至零；纵向位移表现为拉伸变形；且位移峰值出现在桥梁中部处，为2.08 mm。

3 列车荷载下附加挠曲力计算及变形分析

考虑到桥上列车荷载工况较复杂，本节仅对单线全桥加载时的无载侧和有载侧进行计算分析。

3.1 附加挠曲力计算结果分析

无载侧与有载侧钢轨附加挠曲力分别如图5，图6所示，在各墩/台顶的计算结果如表3所示。

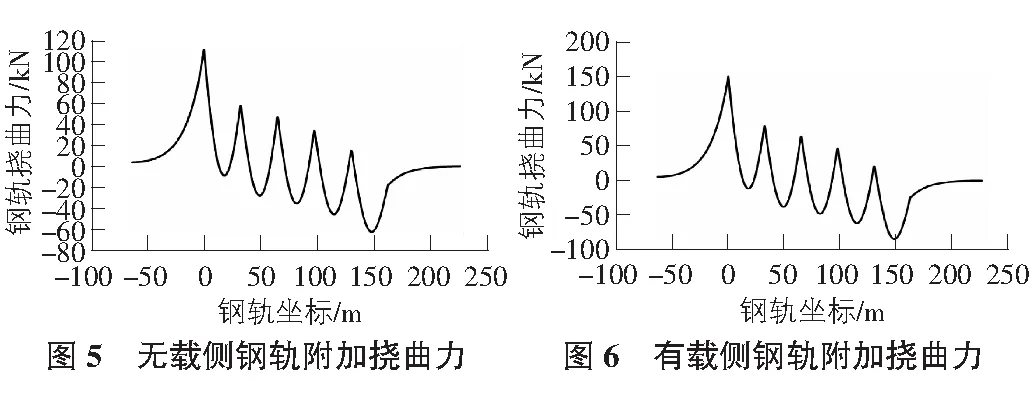
表3 各墩/台顶钢轨附加挠曲力 kN

由图5,图6及表3可知，列车荷载作用下有载侧与无载侧的钢轨附加挠曲力的变化趋势大体相同，且除1号桥台外，其余墩台位置处附加挠曲力均表现为拉力、在每跨跨中位置处均表现为压力，与此同时，拉、压力峰值分别出现在0号桥台位置处与最后1跨跨中位置处，且有载侧较无载侧略大。

3.2 纵向位移计算结果分析

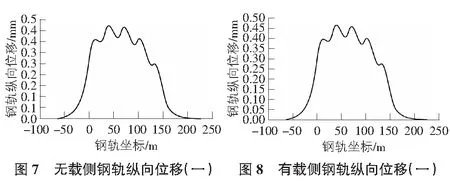
无载侧与有载侧钢轨纵向位移分别如图7,图8所示，在各墩/台顶的计算结果如表4所示。

由图7,图8及表4可知，有载侧与无载侧的钢轨纵向位移的变化趋势均呈先增后减，其位移在两侧路基段逐渐减小至零；钢轨挠曲位移表现为拉伸变形，且有载侧较无载侧略大。

表4 各墩/台顶钢轨纵向位移(二) mm

4 列车制动荷载下制动力计算及变形分析

4.1 制动力计算结果分析

无载侧与有载侧钢轨制动力分别如图9，图10所示，在各墩/台顶的计算结果如表5所示。

表5 各墩/台顶钢轨制动力 kN

由图9,图10及表5可知，列车制动荷载作用下钢轨制动力在桥台处最大，桥梁中部几乎为0；有载侧与无载侧的钢轨制动力的变化趋势大体相同，且均在桥梁前半部分表现为拉力、后半部分表现为压力；有载侧的钢轨制动力与无载侧基本相同。

4.2 纵向位移计算结果分析

无载侧与有载侧钢轨纵向位移分别如图11,图12所示，在各墩/台顶的计算结果如表6所示。

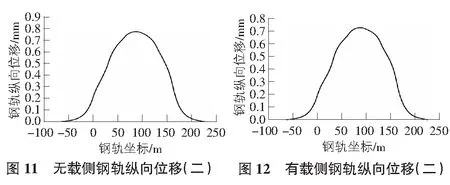
表6 各墩/台顶钢轨纵向位移(三) mm

由图11,图12及表6可知，有载侧与无载侧的钢轨纵向位移的变化趋势均呈先增后减，其位移在桥梁中部位置处取到最大，在两侧路基段逐渐减小至零；纵向位移表现为拉伸变形。

5 结论与建议

本文建立了5跨简支梁桥上板式无砟轨道无缝线路整桥双线空间耦合有限元模型，分别计算了钢轨在梁体温度荷载、列车荷载及制动荷载作用下的附加纵向力及纵向位移，并对无载侧与有载侧各墩/台顶的钢轨纵向力及位移大小进行了对比分析。得>出以下几点结论：

1)钢轨附加伸缩力在左桥台和右桥台处分别达到拉力和压力的最大值；其纵向位移呈先增后减的趋势，并在两侧路基段逐渐减小至零。

2)列车荷载作用下有载侧与无载侧的钢轨附加挠曲力和纵向位移的大小和变化趋势基本相同，其中有载侧较无载侧略大；除1号桥台外，其余墩台位置处钢轨附加挠曲力均表现为拉力、在跨中位置处均表现为压力，且拉、压力峰值分别出现在0号桥台位置处与最后1跨跨中位置处；钢轨纵向位移的变化趋势均呈先增后减，其位移在两侧路基段逐渐减小至零。

3)列车制动荷载作用下有载侧与无载侧的钢轨纵向力及位移的大小和变化趋势基本相同；钢轨纵向力由拉力逐渐表现为压力，并在两侧桥台处达到最大；钢轨纵向位移均表现为拉伸变形，并呈先增后减的趋势，且在桥梁中部达到最大，在两侧路基段逐渐减小至零。

[1] Dieterman H A,Van M A,Van Damm A J P,et al.Longitudinal forces in railroad structures[J].Rail Engineering International,1990,1(6):46-53.

[2] 马战国.既有线简支梁桥无缝线路计算分析[J].铁道建筑,2006(7):77-79.

[3] 耀 荣.无缝线路研究与应用[M].北京：中国铁道出版社,2004.

[4] 蔡成标.高速铁路特大桥上无缝线路纵向附加力计算[J].西南交通大学学报,2003,38(5):609-614.

[5] 宋照清.多跨简支梁桥上无缝线路纵向力研究[D].北京：北京交通大学,2011.

[6] 唐 乐,朱 彬.无碴轨道桥上无缝线路纵向力研究[J].铁道标准设计,2006(z1):81-82.

[7] 孔文斌,雷晓燕.高速铁路长大桥梁无缝线路附加挠曲力计算分析[J].华东交通大学学报,2011(1):25-28.

[8] 戴公连,朱俊樸,闫 斌.30 t轴重重载铁路简支梁桥上无缝线路纵向力研究[J].土木工程学报,2015,48(8):60-69.

[9] 张鹏飞,桂 昊,高 亮,等.简支梁桥上Ⅰ型板式无砟轨道挠曲受力与变形[J].铁道工程学报,2017,34(5):15-19.

[10] 陈 扬，李成辉.桥上CRTSⅠ型板式无砟轨道纵向力分析[D].成都：西南交通大学,2009.

[11] 江海波,吴 迅.城市轨道交通桥梁无缝线路纵向力的空间一体化模型分析[J].城市轨道交通研究,2003,6(1):33-37.