叶片交错布置对双吸泵空化性能的影响分析
韩 伟 郑 昊 王丽琼 张振中 苏 敏
(1.兰州理工大学能源与动力工程学院, 兰州 730050; 2.甘肃省流体机械重点实验室, 兰州 730050;3.山东双轮股份有限公司, 威海 264203; 4.兰州理工大学电气工程与信息工程学院, 兰州 730050)
引言
双吸离心泵具有单机流量大、扬程高、结构简单、便于维修等特点[1],应用于诸多领域。在水力机械中,大部分情况下空化是一种有害的现象,长时间在空化条件下工作,将破坏过流部件,改变流道内的速度分布,导致效率下降、泵的扬程降低,引起机器振动,产生噪声,甚至影响泵的安全运行[2]。因此,如何进一步改善双吸离心泵的空化性能,是水力机械重点研究方向之一。
LI等[3]通过采用仿真软件Pumplinx及完全空化模型对双吸离心泵进行数值模拟分析并与试验进行对比,结果表明,Pumplinx软件在分析离心泵的流动和空化特性时具有一定的可靠性;董兴华等[4]采用数值模拟和外特性试验相结合方法,在空化条件下对双吸泵进行多工况下的定常数值研究,结果表明流量、叶轮结构和双蜗壳结构对双吸泵空化发展有影响;YAO等[5]通过试验分析在非空化和空化条件下,双吸离心泵在半螺旋吸水室和压水室中的压力波动频率变化,并通过分析频谱和时间频域研究了空化条件下的水动力响应;MENG等[6]在设计流量和大流量对双吸离心泵进行数值模拟并进行试验验证,结果表明,数值模拟可以较准确地预测在双吸离心泵的空化现象且在空化条件下在叶片背面会产生微型旋涡;肖若富等[7]通过采用数值模拟和试验研究相结合的方法,研究在变流量工况下长短叶片复合叶轮和常规叶轮在中比转数双吸离心泵下的空化性能,并通过对叶轮内部空化流场分析寻求提高空化性能的方法;刘建瑞等[8]通过对5种叶片交错角度进行数值分析并与试验进行对比,研究了交错叶片对双吸离心泵压力脉动特性的影响;雷明川等[9]基于RNGk-ε湍流模型对3种方案的叶轮叶片交错布置进行三维非定常湍流流场数值分析,研究了双吸离心泵蜗壳内的压力脉动分布规律。
在双吸离心泵叶轮叶片交错布置的研究过程中,有关空化性能的相关问题研究尚不多见。本文为更好地研究叶轮叶片交错角度对泵空化性能的影响,以6叶片双吸叶轮为研究对象,相邻叶片夹角为60°,选取叶片交错角为 0°、10°、15°、20°、30°等5组角度在设计工况条件下对其分别进行研究。
1 数值计算
1.1 建模及网格划分
以250GS80型双吸离心泵作为研究对象。其中,叶轮叶片数Z=6,叶轮叶片交错角度为30°,叶轮出口直径为490 mm。为研究叶轮叶片交错角度对空化性能的影响,叶轮保持原设计参数不变,改变叶轮叶片交错角度,选取交错角度分别为0°、10°、15°、20°、30°(图1)5组叶轮方案进行数值分析。

图1 双吸离心泵叶轮方案Fig.1 Impeller models of double-suction centrifugal pump
为了突出研究结论的共性,引入交错度的定义。双吸叶片交错度计算公式为
θ=β/φ
式中φ——双吸叶轮最大交错角
β——双吸叶轮相邻叶片交错角
由几何结构可知,6叶片双吸叶轮最大交错角φ为30°,因此上述选取交错位置的交错度分别为0、1/3、1/2、2/3和1。
为使数值模拟尽可能接近于真实试验,通过分析CFD误差产生机理及加工工艺需求得,在流动空间建模过程中应考虑腔体、工艺圆角等易忽视因素以消除物理模型近似误差[10]。为使泵进、出口水流速度保持均匀,不影响水泵效率,以泵实际管路安装要求,在进、出口处安装长度为水管口径3倍以上的直管。分别取进口延伸段管长800 mm,出口延伸段管长500 mm,进行水体绘制并组装,其组装图如图2所示。

图2 双吸离心泵三维水体模型Fig.2 Three dimensional wave model of double-suction centrifugal pump1.进口延伸段水体 2.吸水室水体 3.压水室水体 4.出口延伸段水体 5.叶轮水体 6.泵腔水体
非结构化网格能生成高质量的网格,易控制网格大小和节点密度,有利于进行网格自适应,提高计算精度[11]。因此对吸水室、叶轮、压水室等部件水体采用非结构化网格划分,并在扭曲较大处进行局部网格加密。
在通常的计算中,离散误差随网格变细而减小,但由于网格变细时,离散点数增多,舍入误差也随之加大。为使数值计算更具有准确性,在设计工况条件下选取6组不同数量网格进行无关性验证,网格数量分别为153.055万、218.765万、326.675万、457.742万、570.803万、704.065万。根据数值模拟结果绘制出图3所示曲线,从图中可以看出,当网格数量不小于457.742万时,泵扬程、效率之间的误差波动均小于0.15%,因此选用网格数量为457.742万的网格模型作最终分析。
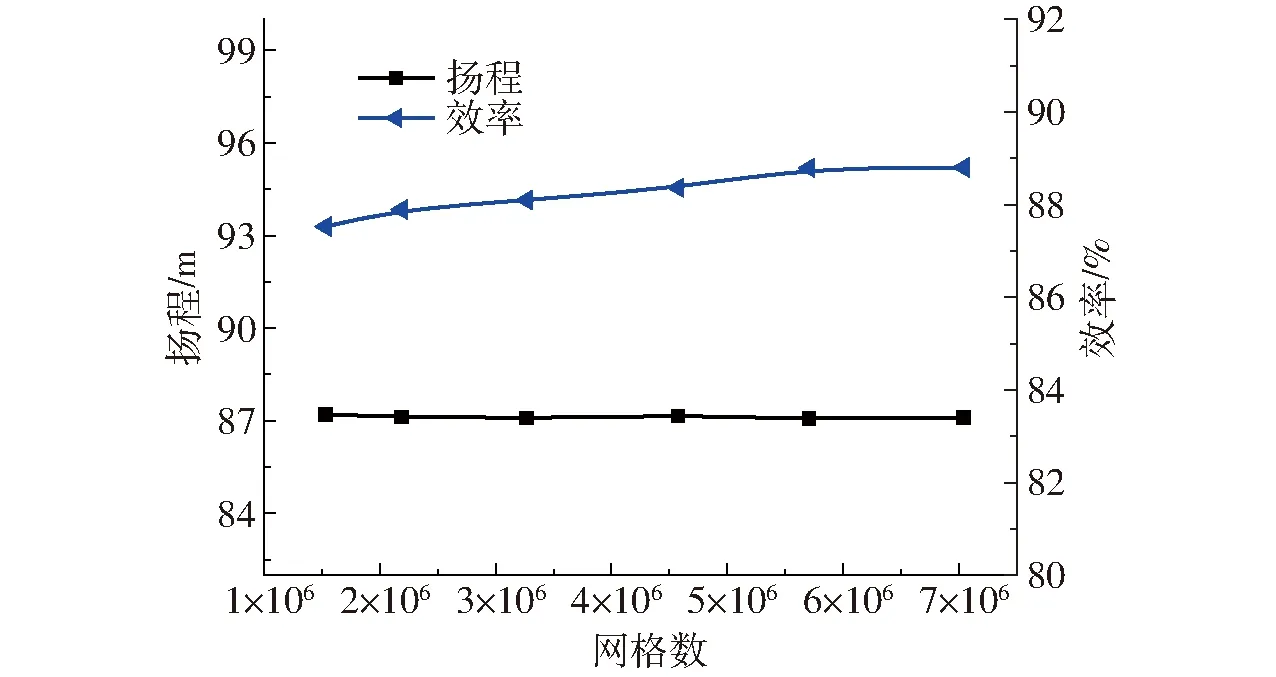
图3 网格无关性检查Fig.3 Mesh independence check
1.2 边界条件
由于泵结构中含有较多弯曲部位,因此湍流模型选用RNGk-ε模型,它既考虑了修正湍动粘度,又考虑了平均流动中的旋转及旋流流动情况。通过在大尺度运动和修正后的粘度项体现小尺度的影响,可以更好地处理高应变率及流线弯曲程度较大的流动[12]。为验证所选湍流模型的准确性,选择多重参考系MRF(Multiple reference frame),定义叶轮计算域为旋转坐标系,进口管、吸水室、压水室、出口管和泵腔计算域为静止坐标系,设置进口条件为速度进口,且假定进口速度在轴向均匀分布;出口条件设置为质量流量出口,壁面采用无滑移边界条件,在近壁区采用标准壁面函数进行外特性数值模拟。
在分析不同叶片交错度对泵空化特性影响时,进口条件设置为总压进口;出口条件设置为质量流量出口,设定进口边界中气相体积分数为0,液相体积分数为1,水的汽化压力为3 540 Pa,收敛精度为10-6。计算时,将单相流动的计算收敛结果作为空化流动计算的初始值以节省空化计算时间,选用基于Rayleigh-Plesset方程的Zwart空化模型[13],保持出口质量流量不变,通过逐渐降低进口总压,以实现双吸离心泵内部的空化性能的模拟。
2 计算结果与分析
2.1 数值模拟与试验对比
为便于数值模拟结果与试验读取值进行对比,搭建如图4所示的试验台,对双吸叶轮交错度为1的研究对象,进行外特性和空化特性试验结果测试。

图4 试验台布置示意图Fig.4 Schematic diagram of test bench1.水封闸阀 2.水箱 3.真空表 4.双吸离心泵 5.转速转矩仪 6.电动机 7.压力表 8.流量计 9.真空泵 10.调节阀
根据叶片泵外特性计算方法[14],泵扬程为
(1)
式中pin——泵进口总压力,Pa
pout——泵出口总压力,Pa
ρ——流体密度,kg/m3
g——重力加速度,m/s2
泵效率为
η=ρgQH/(Mω)×100%
(2)
式中M——叶轮绕轴产生的总力矩,N·m
ω——叶轮旋转角速度,rad/s
Q——流体体积流量,m3/s
在数值模拟过程中选取与双吸离心泵试验时流量相同的5个工况点进行外特性数值模拟计算,由式(1)、(2)计算得出扬程和效率。绘制出外特性曲线对比图(图5),从图5可以得出,泵数值模拟值与试验值的变化趋势基本一致,模拟扬程与试验扬程偏差最大时达1.61%, 模拟效率与试验效率偏差最大时达1.27%。存在的偏差主要来自于数值模拟时未考虑试验时机械损失、表面粗糙度等因素的存在。

图5 交错度为1的双吸泵性能曲线Fig.5 Pump performance curves at staggered degree of 1
泵有效空化余量计算公式[15]为

(3)
式中pva——饱和蒸汽压力,Pa
vj——进口速度,m/s

图6 交错度为1的双吸泵空化断裂特性曲线Fig.6 Cavitation fracture performance curves at staggered degree of 1
将单相无空化计算结果作为空化流动计算的初始值,在最优设计工况点进行双吸离心泵的空化流动数值模拟,绘制出空化曲线对比图(图6),从图中发现,数值模拟与试验的变化趋势基本一致。未空化时,数值模拟扬程与试验扬程的绝对误差为1.23%;取扬程下降3%时所对应的有效空化余量作为泵的临界空化余量,则试验与数值模拟的有效空化余量分别为3.030 m和2.902 m。数值模拟临界空化余量比试验所测值小4.22%。偏差主要来自于数值模拟忽视了汽液相之间的相对速度和相变的热效应破裂等因素的变化[16-17]。
通过在双吸叶轮叶片交错度为1下进行的试验与数值模拟对比发现,两者误差较小,变化趋势基本一致,表明所选数值计算方法能较为准确地进行泵的外特性和空化特性的预测。
2.2 叶片交错布置时空泡体积分数
图7为不同有效空化余量下叶轮中间流面内的空泡分布,从图中可以看出,空泡首先在叶轮叶片进口边背面低压区附近产生,这是因为进口边背面的圆周速度大于进口其他位置,由速度三角形可知,其进口压力损失及进口绕流引起的压降相应变大;叶轮流道为光滑曲面,介质由于叶轮高速运转易产生离心力加快流动速度,在叶片进口边,由于叶轮未对液体做功,根据伯努利方程守恒,则压力会随着速度的增大而减小,在低压区液体易发生空化。并且叶轮不同流道内的空泡分布不均匀,这是因为双吸离心泵中螺旋形压水室就是为了入流均匀,但实际上即使螺旋形压水室也没有达到入流的绝对均匀一致,从而使得叶轮叶片表面的压力分布不对称。随着有效空化余量的减小,泵内部的空泡含量逐渐增大,沿叶片背面向出口方向扩散,并向叶片工作面扩展。通过对比,当有效空化余量为5.552 m时,双吸叶片交错度为1/3和1/2的部分流道中叶轮叶片背面已发现少许空泡,在交错度为0、2/3、1中未发现空泡;随着有效空化余量下降不同交错度叶轮中开始有空泡产生且在不同流道区域中分布不均,当有效空化余量为2.799 m时,从图7中可知,气体体积分数0.9~1.0随无量纲径向位置r/R(r表示径向位置,R表示叶轮外径)的分布位置:交错度为0时分布在0.482~ 0.818之间且不同叶轮流道分布程度不同;交错度为1/3时分布在0.482~0.836之间;交错度为1/2时分布在0.473~0.873之间;交错度为2/3时分布在0.463~0.909之间;交错度为1时分布在0.473~0.727之间且不同叶轮流道分布程度不同。与此同时,交错度为1/3、1/2和2/3时空泡占据叶轮流道大约80%的区域,完全发生空化,破坏泵内的能量转换过程。

图7 叶轮中间流面内空泡分布Fig.7 Vapor distributions on middle stream surface of impeller
同一交错度下,随着有效空化余量的降低叶轮流道中的空泡含量逐渐增加;同一有效空化余量下的不同交错度中空泡含量不同,当有效空化余量为2.799 m,低于临界空化余量时,交错度为2/3中空泡含量相对最多,其次为1/2、1/3、0,交错度为1时相对最少。
2.3 不同交错度下泵扬程变化
从图8中可以看到:随着有效空化余量的减小,扬程先基本保持不变,当有效空化余量减小到一定值时,不同交错度下扬程会不同程度减小。这是因为随着有效空化余量逐渐减小,叶轮叶片背面进口靠近轮缘处有空泡产生,双吸离心泵开始发生空化,但此时有效空化余量仍较大于临界空化余量,泵的扬程变化波动不大;随着有效空化余量继续减小,当有效空化余量小于临界空化余量后,离心泵空化加剧,产生了大量的空泡,堵塞了流道,破坏流动连续性,导致离心泵的扬程急剧下降。
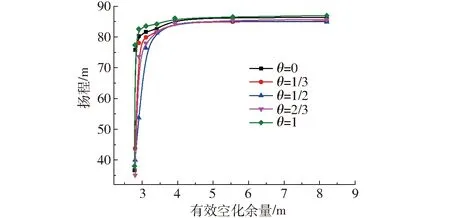
图8 不同交错度下泵扬程变化曲线Fig.8 Head curves of pump at different staggered degrees
通过图8中对比可以发现:不同交错度下泵的空化曲线变化趋势与试验和理论基本一致。有效空化余量大于5.552 m时,双吸离心泵扬程变化基本趋于稳定,交错度为1的扬程分别比交错度为0、2/3、1/3、1/2的扬程高0.72%、1.57%、2.19%、2.26%。从图中可以看出,不同交错度下双吸离心泵的临界空化余量不同,交错度为1的临界空化余量分别比交错度为0、1/3、1/2、2/3小14.94%、16.19%、18.89%、19.68%。当有效空化余量继续下降,由于空泡含量的增多导致流动连续性遭到破坏,泵扬程急剧下降。当有效空化余量为2.789 m时交错度为1的叶轮扬程也开始急剧下降。这表明2.789 m为各种交错度下改型双吸叶轮的极限空化余量。
2.4 不同交错度下叶轮所受的扭矩变化
图9为不同叶轮叶片交错度在设计工况下发生空化时双吸离心泵叶轮所受扭矩的变化曲线。由理论分析知,泵在运转中,叶轮内部的压力是不同的,进口处压力较低,出口处压力较高。若其过流部件的局部区域因为某种原因,抽送液体的绝对压力降至当时温度下的液体汽化压力时,液体便在该处开始汽化,形成空泡,当含有大量空泡的液体向前流经叶轮内的高压区时,空泡周围的高压液体致使空泡急剧地缩小以至破裂。在空泡凝结的同时,液体质点将以高速填充空穴,发生互相撞击而产生水击,使得叶轮叶片受力突然增大,从而使得叶轮所受扭矩变大。因此随着有效空化余量的降低,叶轮所受扭矩先基本保持稳定,当开始发生空化时叶轮所受扭矩逐渐增大,随着空化现象的继续发展,叶轮载荷突降,导致叶轮所受扭矩先增大然后降低。当空化发展至严重空化时叶轮破损严重扭矩发生急剧下降。

图9 不同交错度下叶轮的扭矩变化曲线Fig.9 Torque curves of impeller at different staggered degrees
从图9中可以看出,有效空化余量大于5.552 m时,双吸离心泵扭矩的变化基本趋于稳定,交错度为1的扭矩分别比交错度为0、2/3、1/3、1/2的扭矩高0.31%、0.65%、0.76%、1.33%。随着有效空化余量的降低,不同交错度的叶轮扭矩出现不同的变化趋势,交错度为1、2/3和1/3的变化幅度不大,其中,交错度为1的叶轮所受的扭矩变化较为稳定,交错度为1/2时,叶轮的扭矩变化幅度较大,扭矩下降最明显。这是由于在临界空化状态时发生完全空化时,交错度为1/2发生完全空化区域占据叶轮流道最多,交错度为1发生完全空化区域最少,完全空化的发生使得叶轮叶片受力发生不同程度的改变;当叶轮完全空化时,叶轮受损严重,流体流动性被破坏,导致叶轮所受扭矩急剧下降,从图9中可知,交错度为1/2的叶轮所受扭矩最早急剧下降,而交错度为1的叶轮最迟,这表明在空化状态下,扭矩急剧下降时交错度为1/2的叶轮中的损失较大,交错度为1的叶轮中损失最小,交错度为1时叶轮扭矩急剧下降点的有效空化余量与交错度为0、2/3、1/3、1/2的叶轮扭矩急剧下降点绝对误差分别为0.17%、3.89%、7.15%、10.21%。当有效空化余量为2.789 m,交错度为1时叶轮所受扭矩开始急剧下降,因此,这5种不同交错角度下叶轮扭矩产生陡降对应的有效空化余量均不同。
2.5 不同有效空化余量下静压变化分析
由式(3)可知,当叶轮进口压力小于当地温度水饱和蒸汽压力时,静压低于当地温度水饱和蒸汽压力所在区域会发生完全空化。图10给出了不同有效空化余量下叶轮流道内的静压分布,其中红色区域为静压高于当地温度水饱和蒸汽压力的部分,其余为小于等于当地汽化压力的部分。从图中可以看出,相同有效空化余量下叶轮中间流面发生完全空化的面积在不同交错度中是不相同的。当有效空化余量为3.921 m时,不同交错度叶轮流道中存在完全空化区域且在不同流道区域中分布不均,交错度为1时汽相体积分数约占叶轮流道5%的区域,交错度为2/3中含量最少。随着有效空化余量的减小,当有效空化余量为2.799 m时,交错度为0和1时发生完全空化区域较小且各流道间分布不均匀,其中交错度为1发生完全空化区域最少,约占叶轮流道15%;交错度为1/3、1/2和2/3中完全发生空化区域基本填充各个叶轮流道,其中,交错度为2/3发生完全空化区域占据叶轮流道最多,约占80%。

图10 不同有效空化余量下静压分布区域Fig.10 Static pressure distributions at different NPSH
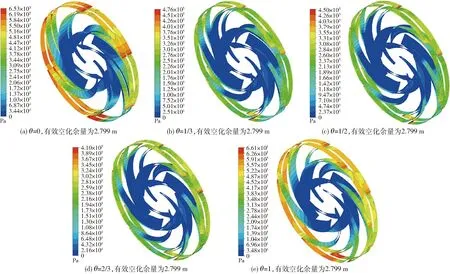
图11 不同交错度叶片表面和叶轮出口面静压分布Fig.11 Static pressure distributions of blade surface and impeller outlet surface at different staggered degrees
通过分析当有效空化余量为2.799 m时不同交错度下叶轮叶片表面和叶轮出口面静压云图(图11)可以看出:叶轮出口处从背面到工作面存在着明显的压力梯度,方向指向工作面。当叶轮交错度为0时,双吸叶轮两侧工作面与工作面,背面与背面完全重合,双吸叶轮两侧出口处压力沿叶轮隔板呈对称分布,叶轮出口两侧基本无压差存在。双吸叶轮两侧出口压力无法进行相互补偿,导致叶轮流道内压力以较大梯度变化;当交错度为1/3、1/2和2/3时,双吸叶轮一侧工作面附近出流为高压区,由于叶轮叶片交错布置,该侧叶轮高压区出流将对应另一侧叶轮背面低压区,由于压差的存在,一侧叶轮出口高压区与另一侧叶轮低压区进行非对称性压力补偿,从而影响叶轮流道内局部区域压力变化。相对于交错度为0的对称布置双吸叶轮,交错度为1/3、1/2和2/3的流道内压力梯度更大,使得叶轮流道内的流动形态变得更加紊乱,能量损失增加,低于临界空化压力的区域相应增加,这样反而进一步加剧了空化的发生。其中交错度为2/3时,在已研究的交错度范围内,叶轮出口处的非对称性压力补偿对叶轮内压力梯度的负面影响达到最大,空化最严重,这也与空化断裂特性一致;当交错度为1时,双吸叶轮两侧叶片为对称交错布置,一侧高压区与另一侧低压区形成对称性压力补偿,有效降低了两侧流道内的压力梯度,降低了叶轮内流动损失,也在一定程度上减少了低于临界空化压力的区域,从而有助于减小叶轮内空化的严重程度。
因此可以得出,该型双吸离心泵当叶轮叶片交错度为1时,空化性能相对最好。
3 结论
(1) 通过数值模拟与试验对比知,两者误差较小,模拟扬程与试验扬程偏差最大时达1.61%, 模拟效率与试验效率偏差最大时达1.27%;临界空化余量数值模拟比试验值小4.22%,数值模拟值与试验数据的变化趋势基本一致,所选数值计算方法能较为准确地进行泵外特性和空化特性的预测。
(2) 同一交错度下,随着有效空化余量的降低叶轮流道中的空泡含量逐渐增加;同一有效空化余量下的不同交错度中空泡含量不同,当有效空化余量为2.799 m,小于临界空化余量时,交错度为2/3时空泡含量最多,其次依次为1/2、1/3、0,交错度为1时相对最少。
(3) 发生空化断裂时,5种不同交错度下双吸叶轮扭矩和扬程急剧下降时对应的有效空化余量均不同,表明双吸叶轮的交错度对其空化性能有不同程度的影响。
(4) 当有效空化余量低于临界空化余量、双吸叶轮叶片交错度为2/3时,发生完全空化区域占据叶轮流道最多,交错度为1时发生完全空化区域最少。因此对该型双吸叶轮而言,交错度为1时双吸离心泵的空化特性相对最好。
1 丁成伟.离心泵与轴流泵原理及水力设计[M].北京:机械工业出版社,1981:5-6.
2 张克危.流体机械原理[M].北京:机械工业出版社,2012:137-170.
3 LI P, HUANG Y F, LI J. Cavitation simulation and NPSH prediction of a double suction centrifugal pump[C]∥IOP Conference Series: Earth and Environmental Science, 2012,15(6):2025.
4 董兴华,毕祯,周栋,等.双吸离心泵叶轮空化流动预测的数值分析 [J]. 西华大学学报,2016,35(6):17-22.
DONG Xinghua, BI Zhen, ZHOU Dong, et al. The prediction and numerical simulation of impeller cavitation performance in double suction pump [J].Journal of Xihua University, 2016,35(6): 17-22. (in Chinese)
5 YAO Z F, WANG F J, XIAO R F, et al. Experimental investigation of pressure instabilities affected by cavitation for a double-suction centrifugal pump[C]∥IOP Conference Series: Earth and Environmental Science, 2012, 15(6): 2040.
6 MENG G, TAN L, CAO S L, et al. Numerical simulation and analysis of cavitation flows in a double suction centrifugal pump[C]∥IOP Conference Series: Materials Science and Engineering,2015,72(3):2020.
7 肖若富,王娜,杨魏,等.复合叶轮改善双吸式离心泵空化性能研究[J/OL].农业机械学报, 2013, 44(9): 35-39. http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?file_no=20130907&flag=1.DOI:10.6041/j.issn.1000-1298.2013.09.007.
XIAO Ruofu, WANG Na, YANG Wei, et al. Improvement of cavitation characteristics of double suction centrifugal pump with compound impeller [J/OL].Transactions of the Chinese Society for Agricultural Machinery, 2013,44(9):35-39.(in Chinese)
8 刘建瑞,付威,高振军,等.交错叶片对双吸离心泵性能影响的数值分析[J].排灌机械工程学报,2015, 33(3):196-202.
LIU Jianrui, FU Wei, GAO Zhenjun, et al. Numerical analysis of effects of staggered blades on characteristics of double- suction centrifugal pump[J].Journal of Drainage and Irrigation Machinery Engineering, 2015, 33(3):196-202. (in Chinese)
9 雷明川,赖喜德,宋冬梅,等.交错叶片叶轮对双吸离心泵蜗壳内压力脉动的影响研究[J].中国农村水利水电,2014(7):177-181.
LEI Mingchuan, LAI Xide, SONG Dongmei, et al. A study of staggered arrangement blades on the pressure pulsation of a double-entry pump with volute casing [J].China Rural Water and Hydropower,2014(7): 177-181. (in Chinese)
10 JOHN D DENTON. Some limitations of turbo machinery CFD [C]∥ASME Turbo Expo 2010: Power for Land, Sea and Air, 2010,7:735-745.
11 刘厚林,董亮,王勇,等.流体机械CFD中的网格生成方法进展[J].流体机械,2010,38(4):32-37.
LIU Houlin, DONG Liang, WANG Yong, et al. Overview on mesh generation methods in CFD of fluid machinery [J]. Fluid Machinery,2010,38(4):32-37. (in Chinese)
12 王福军.计算流体动力学分析——CFD软件原理与应用[M].北京:清华大学出版社,2010:124-125.
13 曹玉良,贺国,明廷锋,等.水泵空化数值模拟研究进展[J].武汉理工大学学报,2016,40(1):55-65.
CAO Yuliang, HE Guo, MING Tingfeng, et al. Review on numerical simulation of pump cavitation [J]. Journal of Wuhan University of Technology, 2016, 40(1):55-65. (in Chinese)
14 董亮,刘厚林.叶片泵CFD数值计算实例详解[M].北京:机械工业出版社,2015:4.
15 施卫东,李通通,张德胜,等. 轴流泵叶轮区域空化特性数值模拟[J].农业工程学报,2012,28(13):88-93.
SHI Weidong, LI Tongtong, ZHANG Desheng, et al. Numerical simulation on cavitation characteristic in impeller of axial-flow pump [J]. Transactions of the CSAE, 2012, 28(13): 88-93. (in Chinese)
16 王秀礼,袁寿其,朱荣生,等.离心泵汽蚀过渡过程瞬态特性分析[J].西安交通大学学报,2012,46(7):38-43.
WANG Xiuli, YUAN Shouqi, ZHU Rongsheng, et al. Analysis on transient hydraulic characteristics of cavitation process in centrifugal pumps[J].Journal of Xi’an Jiaotong University,2012,46(7):38-43. (in Chinese)
17 施卫东,张光建,张德胜,等.水气最大密度比对轴流泵空化计算的影响[J/OL].农业机械学报,2014,45(5):65-70. http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?file_no=20140510&flag=1.DOI:10.6041/j.issn.1000-1298.2014.05.010.
SHI Weidong, ZHANG Guangjian, ZHANG Desheng, et al. Effect of the maximum density ratio between liquid and vapor on cavitation simulation of axial-flow pump [J/OL].Transactions of the Chinese Society for Agricultural Machinery, 2014, 45(5):65-70. (in Chinese)

