大结构参数无底柱分段崩落法结构参数优化研究
孙东东,张治强,2,常 帅,2,路增祥,2,赵 野
(1.辽宁科技大学,辽宁 鞍山 114051;2.辽宁省金属矿产资源高效综合利用工程技术研究中心, 辽宁 鞍山 114051;3.抚顺罕王傲牛矿业股份有限公司,辽宁 抚顺 113001)
无底柱分段崩落法是一种安全、高效、机械化程度较高的采矿方法,在国内外金属矿山地下开采中应用非常广泛[1-3]。随着矿山对开采强度的提高、开采技术水平及矿山机械的发展,高分段大间距成为无底柱分段崩落采矿法重要的研究和发展方向。
无底柱分段崩落采矿法的显著缺点是矿石损失贫化大,为此相关学者进行了大量的研究。张国建等研究了崩落体、放出体及松动体三者的关系对矿石回采指标的影响[4-5];李文增等[6]和任凤玉等[7]根据崩落体理论及随机介质放矿理论的研究成果,阐述了崩落体、残留体与放出体三者形态之间的关系及对矿石回采效果影响,以此提出结构参数优化方案;范庆霞通过工业试验及爆破参数试验,提出了通过优化爆破参数来优化结构参数的思路[8];吴荣高等通过建立回贫差目标函数求极值的方式来确定崩矿步距的最优值[9];王云鹏等建立了以单位工业储量盈利最大化和单位精矿盈利最大化为目标函数的数学模型,为崩矿步距的确定提供依据[10];李彬等[11]和安龙等[12]应用PFC颗粒流软件进行数值模拟,得到矿岩颗粒流动状态及模拟出放出体等形态,进而得出矿石回收率等回采指标与结构参数之间的关系。
毛公铁矿采场采用分段高度为20 m、进路间距为18 m的大结构参数,在生产过程中出现了废石的提前混入,矿石损失贫化大,回收率远远低于设计值的现象。针对这一现象,本文比较不同结构参数下矿石回采指标,进而优化采场结构参数,降低矿石损失贫化。矿山生产实际中分段高度和进路间距在前期采准已经形成,生产过程中难以改变,而崩矿步距灵活可变[13],本文借助崩落体形态与放出体形态的匹配关系分析崩矿步距对矿石回收指标的影响机理,并根据相似原理建立物理模型[14],模型可模拟多分段、多崩矿步距、多回采进路条件下连续放矿,应用物理模型,进行崩矿步距为一排炮孔(1.8 m)和崩矿步距为两排炮孔(3.6 m)两种条件下的模拟放矿实验,并对崩矿步距与矿石回采指标之间的关系进行分析。
1 崩落体形态与放出体形态的匹配关系
根据椭球体放矿理论可知,在截至品位条件下放矿,崩落体形态和放出体形态的匹配关系决定了矿石的回采指标。崩落体的形态好坏可用崩落体放出系数表示,崩落体放出系数即为放出体体积与崩落体体积之比,放出系数越大说明崩落体的形态就越好。崩落体形态和放出体形态的匹配关系对放矿的影响如图1所示。当崩矿步距适中时,放出体形态与崩落体形态基本吻合,放出系数最大,矿石几乎全部放出,如图1(a)所示;当崩矿步距较小时,崩落体形态偏“瘦”,放出系数较小,崩落体形态不能与放出体形态很好的吻合,端部废石会提前到达出矿口,达到截止品位,导致顶部矿石残留,如图1(b)所示;当崩矿步距较大时,崩落体形态偏“胖”,放出系数较小,崩落体形态不能与放出体形态很好的吻合,顶部废石会提前到达出矿口,导致端部矿石残留,这部分残留的矿石和混入的废石会直接影响矿石的回采指标,如图1(c)所示。

图1 崩落体与放出体匹配关系
在生产过程中,崩矿步距直接影响着崩落体的形态,进而影响崩落体形态与放出体形态的吻合程度。混入废石多少及残留矿石可否在相邻分段放出会直接影响各分段的矿石回采指标。为了进一步研究崩矿步距对矿石回采指标的影响,进行了实验室物理模型实验。
2 实验室物理模型实验
2.1 模型的建立
以矿山实际结构参数为基础,根据相似原理制作物理模型,模拟比为1∶50。毛公铁矿分段高为20 m,进路间距为18 m,回采进路尺寸为4.2 m×4.2 m(宽×高)。本模型设计了3个分段,分段高为400 mm,每分段设计3条进路及5个崩矿步距,进路间距为360 mm,炮孔排距为36 mm;巷道尺寸宽、高分别为84 mm、84 mm,实验模型见图2。
2.2 实验过程
实验所用矿石取自毛公铁矿采场,现场取样统计矿石粒径及各类粒径矿石所占比例,如表1所示。
按相似原则确定实验所需的矿石粒径及粒径配比,见表2。按照表2所给粒径配比,将矿石装入模型的各个分段,每个分段的装填高度为400 mm。矿石装填完毕后,装入600 mm高的石英石作为覆盖岩层,图3为矿岩装填后的模型情况。
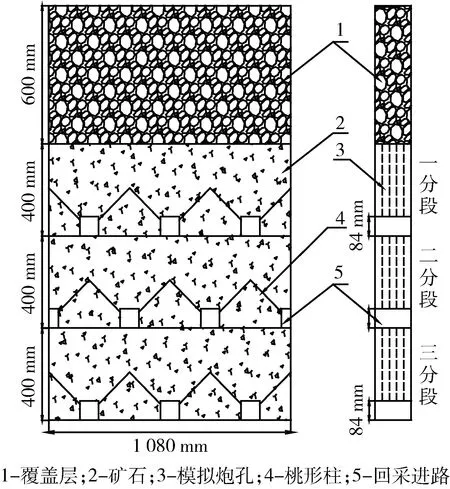
图2 实验模型
表1 现场矿石颗粒级配组成

粒径/m0~0.250.25~0.50.5~1比例/%304030

表2 实验矿石颗粒级配组成

图3 矿岩装填后模型
共进行了两次放矿实验,第一次实验崩矿步距为一排炮孔(1.8 m),第二次实验崩矿步距为两排炮孔(3.6 m);两次实验均保持每个分段中各回采进路平行出矿,用小铲以固定铲掘深度铲出矿(岩),并用电子秤称出矿(岩)总质量,之后利用磁铁将矿石分选出来,分别对分选的矿石和岩石进行称重,最后记录下矿岩总质量、矿石量及岩石量,当单次出矿混岩率达到70%时停止出矿,开始下一步距的出矿,每个分段出矿结束后向模型中充填石英石,使覆盖层高度保持在600 mm左右;重复此步骤直至最后一个分段的最后一个步距出矿结束,图4为出矿结束后的模型情况。
2.3 实验结果分析
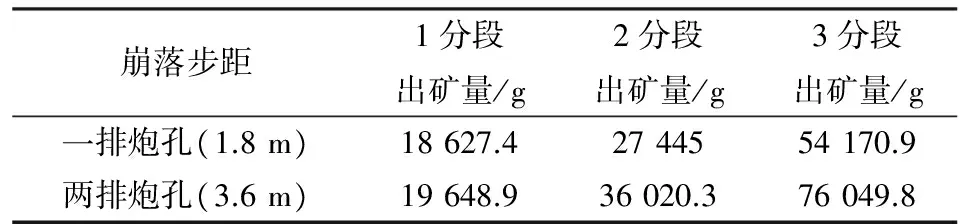
分别统计两次实验中各分段纯矿石放出量,见表3。两次实验中各分段纯矿石放出量对比图,见图5。
分别对两次实验各分段的纯矿石回收量、矿石回收率、矿岩回收总量、废石混入量及混岩率进行统计,见表4和表5。
两次实验各分段矿石回收率及混岩率的对比图,如图6和图7所示。

图4 出矿结束后模型
表3 纯矿石放出量
崩落步距1分段出矿量/g2分段出矿量/g3分段出矿量/g一排炮孔(1.8m)18627.42744554170.9两排炮孔(3.6m)19648.936020.376049.8
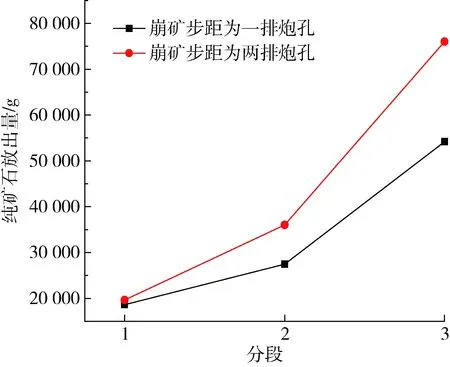
图5 各分段纯矿石放出量
表4 崩落步距为一排炮孔(1.8 m)条件下实验数据

分段矿石回收量/g矿石回收率/%矿岩回收总量/g废石混入量/g混岩率/%144284.544.2873040.928756.439.37281382.558.59126068.444685.935.453136670.6126.31210006.573335.934.92

表5 崩落步距为两排炮孔(3.6 m)条件下实验数据

图6 各分段矿石回收率
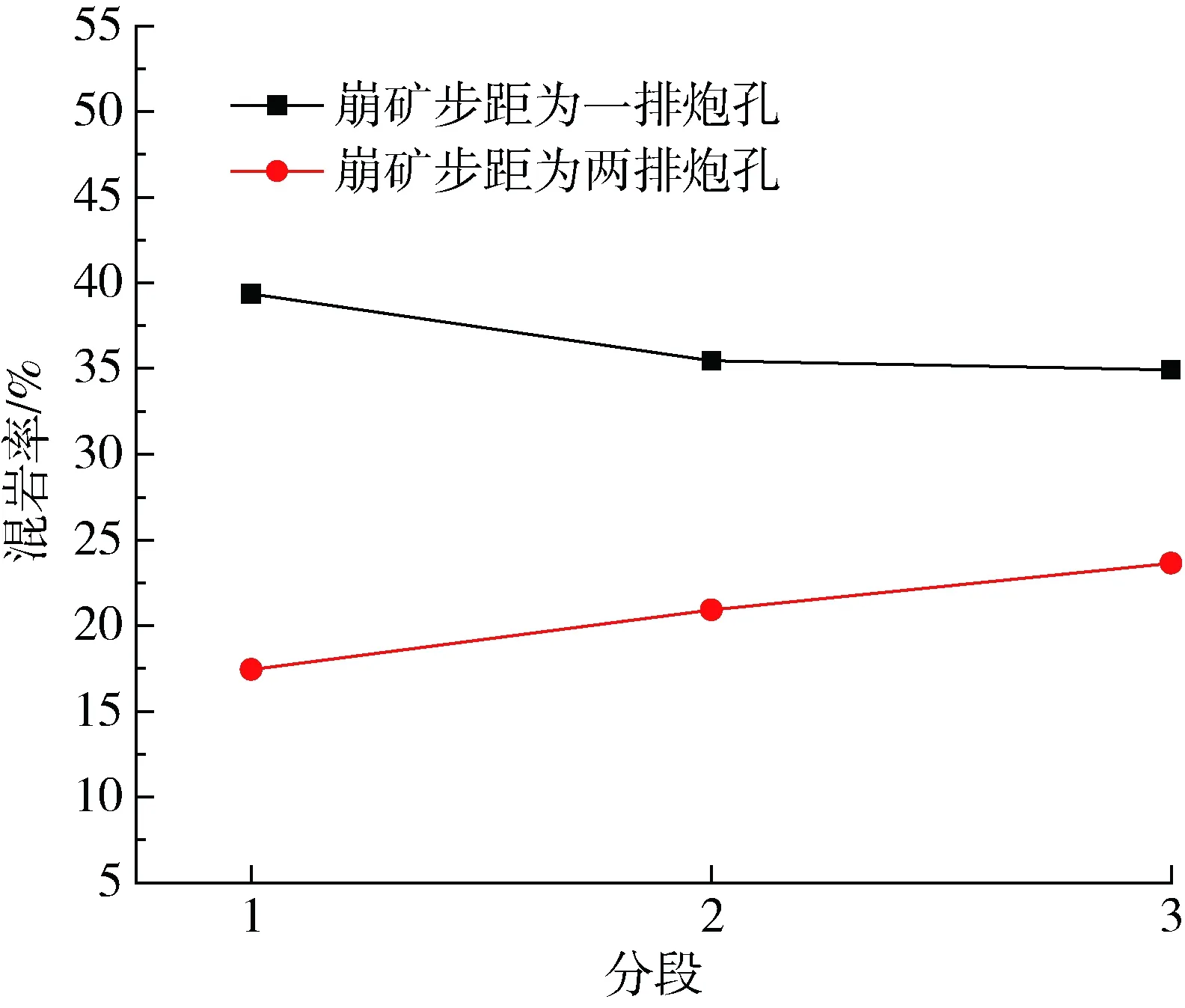
图7 各分段混岩率
通过图5可知,崩矿步距为3.6 m条件下的各分段纯矿石放出量均高于崩矿步距1.8 m条件下的各分段纯矿石放出量,其中一分段高出1 021.5g(5.48%),二分段高出8 575.3 g(31.25%),三分段高出21 878.9 g(40.39%),各分段纯矿石放出量平均高出10 491.9g(24%)。通过图6可知,崩矿步距为3.6 m的各分段矿石回收率均高于崩矿步距为1.8 m的各分段矿石回收率,其中一分段高出2.77%,二分段高出11.21%,三分段高出41.13%,各分段矿石回收率平均高出约18%,其中两次实验的第三分段矿石回收率均超过100%,且第三分段回收率好于第二分段,第二分段好于第一分段,证明散体移动具有空间连续性,上一分段的部分残留矿石会在以后的分段中放出。由图7可知,崩矿步距为3.6 m条件下的各分段的混岩率均低于崩矿步距为1.8 m条件下的各分段混岩率,其中一分段低21.93%,二分段低14.54%,三分段低11.29%,各分段混岩率平均低16%左右。由图5~7综合分析可得,崩矿步距为两排炮孔(3.6 m)条件下的回收指标好于崩矿步距为一排炮孔(1.8 m)条件下的回采指标。
3 结 论
1) 研究表明,崩矿步距为两排炮孔条件下的纯矿石放出量、矿石回收率及混岩率等回收指标要好于崩矿步距为一排炮孔条件下的回采指标,其中各分段矿石回收率平均高出约18%,各分段混岩率平均低16%左右。
2) 在分段高度为20 m、进路间距为18 m结构参数下,崩矿步距为两排炮孔(即3.6 m)条件下的崩落体形态与放出体形态匹配吻合程度好于崩矿步距为一排炮孔(即1.8 m)条件下崩落体形态与放出体形态匹配吻合程度。
3) 实验表明,放矿过程中,散体移动具有空间连续性,上一分段的部分残留矿石会在以后的分段中放出,且3.6 m崩矿步距放出的残留矿石量多于1.8 m崩矿步距。
[1] 余健,汪德文.高分段大间距无底柱分段崩落采矿新技术[J].金属矿山,2008(3):26-31.
[2] 郭雷,熊靓辉.无底柱分段崩落法现状及发展趋势[J].中国矿山工程,2010,39(6):44-48.
[3] 何荣兴,任凤玉,宋德林,等.大结构参数无底柱分段崩落法的发展及技术问题探讨[J].金属矿山,2015(6):1-5.
[4] 张国建,翟会超.无底柱分段崩落法放出体、松动体、崩落体三者关系模型[J].中国矿业,2010,19(3):69-71.
[5] 张国建,蔡美峰.崩落体形态及其影响研究[J].中国矿业,2003,12(12):38-42.
[6] 李文增,任凤玉.弓长岭井下铁矿崩矿步距优化研究[J].中国矿业,2008,17(6):55-57.
[7] 任凤玉,袁国强,陈晓云,等.弓长岭井下矿改进采场结构的研究[J].金属矿山,2006(9):86-87.
[8] 范庆霞.梅山铁矿采场崩矿步距的探讨[J].金属矿山,2007(9):24-27.
[9] 吴荣高,安龙,江学,等.梅山铁矿大结构参数下合理崩矿步距研究[J].金属矿山,2012(5):5-8,12.
[10] 王云鹏,余健.无底柱分段崩落法崩矿步距的优化[J].中南大学学报:自然科学版,2014,45(2):603-608.
[11] 李彬,许梦国,曹华斌,等.无底柱分段崩落法放矿步距优化数值模拟[J].矿业研究与开发,2012,32(2):5-7.
[12] 安龙,徐帅,李元辉,等.基于多方法联合的崩落法崩矿步距优化[J].岩石力学与工程学报,2013,32(4):754-759.
[13] 何荣兴,任凤玉,宋德林,等.无底柱分段崩落法崩矿步距优化方法及应用[J].矿业研究与开发,2015,35(8):1-4.
[14] 王昌汉.放矿学[M].北京:冶金工业出版社,1982:129-145.

