土中未冻含水量与温度关系研究

万旭升， 赖远明， 张明义， 裴万胜

（1.西南石油大学 土木工程与建筑学院，四川 成都 610500；2.中国科学院寒区旱区环境与工程研究所 冻土工程国家重点实验室，甘肃 兰州 730000）

我国多年冻土与季节冻土面积分布广泛，超过全国总面积的2／3［1-3］。在四季气温周期变化过程中，冻土区土壤水分的不断迁移和聚集，反复成冰与溶解，使地基土的物理力学性质发生剧烈变化，给这些地区的交通、工业与民用建筑带来严重的危害。此外，随着冻结施工法在矿井建设、地基基础、地铁、海底隧道等工程中的广泛应用，土中水分冻结研究显得越来越重要。一方面冻结温度是划分土体冻结与否的关键指标，当土体温度降至初始冻结温度以下土中产生冻胀力，从而影响构筑物的基础稳定性；另一方面冻土的水热迁移与成冰过程本质上是多孔多相介质的多场耦合问题［4-6］，而未冻含水量与冻结温度的关系是研究耦合相变问题的关键条件。

未冻含水量的变化规律能够有效揭示土中水分冻结机理。文献［7］首次提出描述多孔介质冰水平衡状态的Clapeyron方程，建立不同温度下冰水压力平衡关系，阐明了水结冰受其水压力影响。文献［8］讨论了广义Clasusius-Clapeyron方程的适用条件，并提出了更能真实反映土体冻结过程的动态模型。

目前，未冻含水量与温度关系研究主要基于试验研究。核磁共振法在冻土未冻含水量测试中得到广泛应用［9］。徐学祖等［2］通过室内试验回归了未冻含水量随温度降低呈幂函数关系，有学者将此关系应用到冻土水热耦合计算中［10］。文献［11］通过大量试验回归出未冻含水量与温度间呈指数关系，并基于此函数关系建立冻土冻胀理论模型。未冻含水量随外部作用（土质、温度及荷载等）的改变而变化，当外部作用稳定时，未冻水变化力图维持平衡状态［3，12］。此外，土中盐分的存在降低冻土的冻结温度，对于易形成结晶盐的盐分，含盐量的增加加剧未冻含水量的变化［13］。

也有学者将水分冻结温度归咎于土水势的变化，未冻含水量随着土水势的增大而不断减小［14］。文献［15］依据Claperyron方程并结合Van-genuchten模型提出未冻含水量在不同温度下的预测模型，但模型参数过多，实用性受限。朱定一等［16］从非平衡力作功出发，推导了反应型固液界面上液滴体积与固液半径和接触角之间的关系。裴万胜［17］基于频域反射法在土中水分测量应用，建立不同土壤类型未冻含水量随温度变化的简单预测模型。而对于冻土，目前很少有未冻水机理的理论模型方面的文献。

鉴于土中水分冻结过程理论研究相对较少，本文针对多孔介质水溶液物理化学特性，通过冰水化学势能平衡原理，提出了依据土体孔隙分布特征计算冻结温度的理想公式。从理论上建立了未冻含水量与温度的关系，可为冻土区工程防冻胀问题及成冰机理提供参考和依据。

1 理论推导

为了更好地研究土中水分冻结，根据土体孔隙分布特征，基于冰水化学势能平衡理论，引入冰液表面自由能，推导了未冻含水量与温度关系。其基本条件及假定如下：（1）土体为饱和；（2）不考虑土中结合水的冻结；（3）未考虑因土体冻结使土体发生的膨胀变形。其基本参数见表1。

表1 基本参数

1.1 冰水化学势

对于纯水，正常大气压下冻结温度为0℃。但是在土中的水大部分存在土体孔隙中，随着冰水压力变化增大，冻结温度会不断下降。冰水相变发生时，对于任何时刻，存在冰水化学势相等。

式中：pw为土中水溶液压力；pi为孔隙中冰压力；T为绝对温度。

在标准大气压下，若水压力发生d pw微小变化，冻结温度从T变化到T＋d T，此时新的平衡方程为

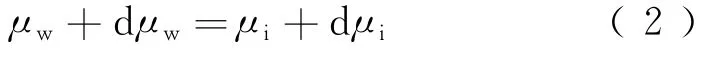
结合式（1）、式（2），可得

对于多组分体系，化学势能为

式中：G为吉布斯自由能；nk为物质的量。

在热力学中，吉布斯自由能是温度、压力和化学势的函数［20］，故式（3）可变为

化学势μk对温度和压力的偏微分为

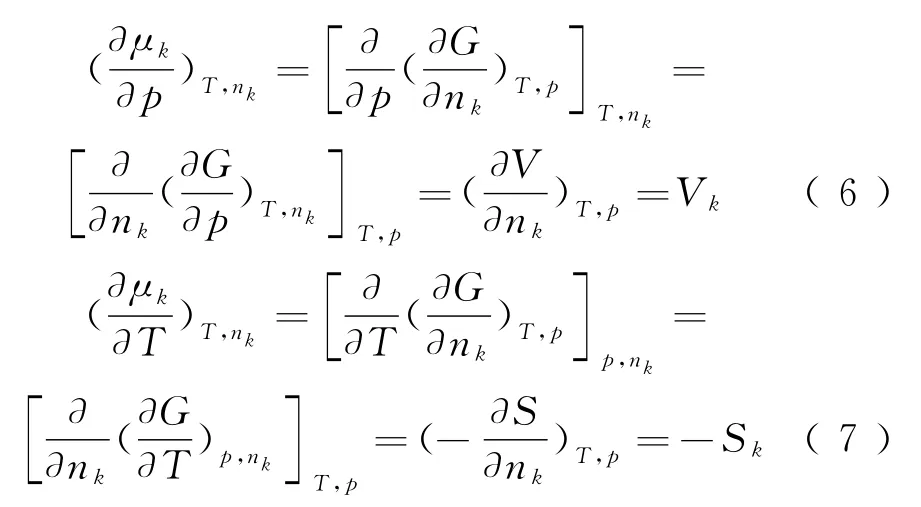
式中：Vk、Sk分别为物质k的偏摩尔体积、偏摩尔熵。对于纯物质（冰和水），可取其摩尔体积vk、摩尔熵。

将式（6）和式（7）代入式（5），可得

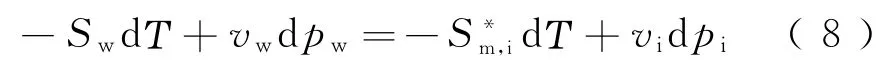
在水溶液中存在

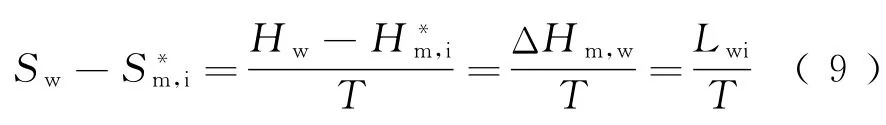
式中：ΔHm，w为冰水相变焓；Lwi为水的结冰潜热。

将式（9）代入式（8），可得

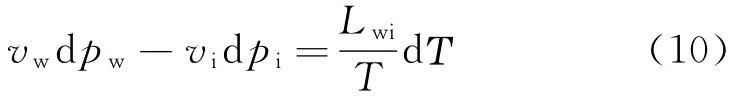
1.2 冰水压力变化下冻结温度

土体可视为一种多孔介质材料，力的平衡满足有效应力原理。在外荷载作用下满足力学平衡［21-23］

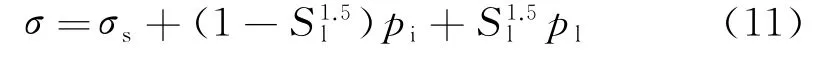
式中：σs为颗粒间接触应力或有效应力；Sl为水分所占孔隙度或孔隙比，即水分所占孔隙的体积比。对于饱和土，土体未冻结时存在Sl＝1。

对于饱和土样，若外荷载不变，外压主要由孔隙压力承担，故只考虑孔隙内压力变化。孔隙水分冻结过程中，水溶液压力与冰压力不断变化 （认为在标准大气压下，水压力为0，水压力的变化相对于标准大气压），在此变化过程中冰压力逐渐增大。所以对式（11）微分，可得

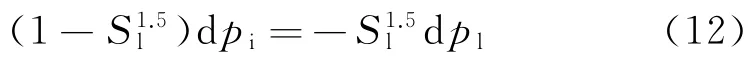
将式（12）代入式（10），化简变形得

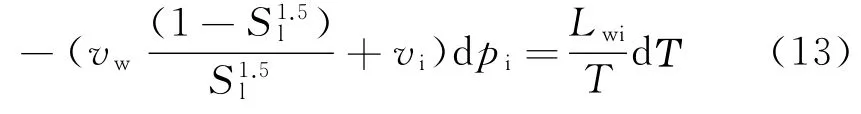
取纯水初始冻结温度为273.15 K，而冰压力初始值为0，当冰压力变化Δpi时，对式（13）进行积分为

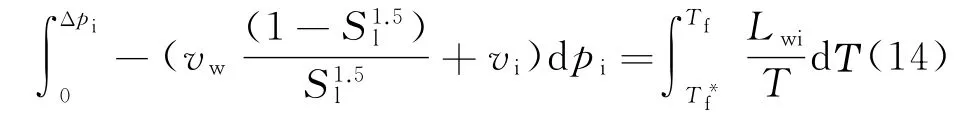
若温度变化较小时，认为冰水相变潜热Lwi为常数，由式（14）可得

式中：Tf为土中自由水的冻结温度。

1.3 理想成冰模型

由于自由水存在土体孔隙中，冰液接触面并非一个平面，接触面上相变平衡必须要考虑接触面冰水自由能。而孔隙中冰晶生长必须具备更高的化学势，要比大体积的冰的化学势高。故存在

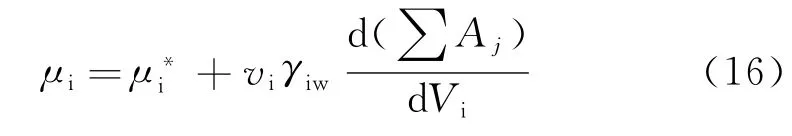
小冰晶接触面上的冰压力变化Δpi时，化学势的变化为

由上表可知，x26,x27的VIF值均大于10，故该两项指标存在共线性，本文在Logistic模型研究中直接剔除该两项指标。

结合式（16）和式（17），可得

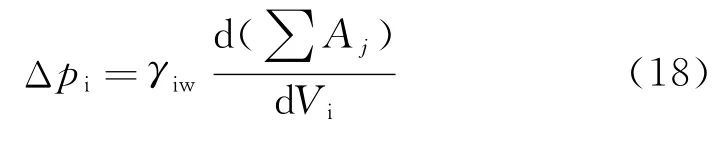
为了使计算模型更加简单，假定冰晶均匀成核，冰液接触面为圆球面，则式（18）可化简为

式中：rcrystal是冰晶结晶半径。

1.4 未冻含水量与温度函数关系建立

孔隙中未冻含水量wuw与水分所占的孔隙度之间存在的关系为

将式（20）代入到式（15）中，可得

式（21）建立了未冻含水量与温度之间的关系，当冰晶结晶半径一定的情况下，未冻含水量与温度之间呈反比例关系。随着温度降低，未冻含水量减小。

冰晶结晶半径受土中孔隙大小的影响，对于任意孔隙，这一动态过程中结晶半径可用孔隙半径与接触角θ表示，冰晶填充孔隙示意图见图1。结晶半径为

式中：rp为孔隙半径，对于自由水冻结过程中，由于水膜厚度很小，可认为自由水所占孔隙的体积近似等于孔隙体积。当孔隙中自由水全部冻结时，其结晶半径近似可认为是孔隙半径。

图1 冰晶填充孔隙示意图

对于任意孔隙水，当自由水完全冻结时，式（21）可表示为

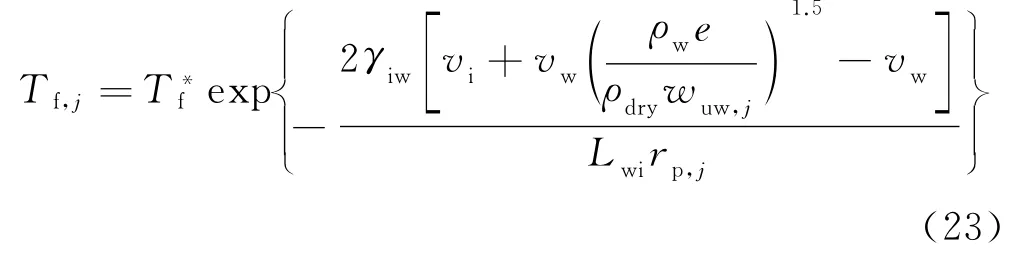
按照孔隙水由大到小的冻结顺序冻结时，冻含水量为

式中：Vj为第j种孔隙体积。若已知土的孔径分布，则可近似计算相应未冻含水量。由式（22）～式（24）可见，当水分从大孔隙开始冻结时，冰液接触面近似为水平面，当其自由水全部冻结时，冻结温度可通过最大孔径计算，若是无盐且黏颗粒含量较少的土，一般可近似为0℃。若考虑土颗粒表面自由能以及土中离子作用，初始冻结温度会小于

0℃。

2 试验验证

2.1 核磁共振试验

核磁共振法是利用试样中的氢核受到射频场的干扰后，测定其松弛时间不同，产生不同强度的信号，得到未冻含水量与温度的关系。

2.1.1 试验条件

本试验采用青藏高原粉质黏土，孔径分布见图2，初始含水量为18%，将土样装至内径为2 cm的聚氯乙烯管中压实，试样高约为5 cm，控制其干密度为1.8 g／cm3以接近天然干密度，孔隙比为0.49，用橡皮塞密封。试样先在冷浴中恒温，然后分阶段降温，等温度恒定后用脉冲核磁共振仪测试可获得土样强度信号，将不同温度下核磁共振强度信号转化为质量含水量即可得到未冻含水量与温度关系曲线。土中水在冻结过程中先要经历过冷阶段［24］，故在冰晶结晶中心温度以上不会发生冰水相变，当温度达到结晶温度后会跳跃到初始冻结温度，为了便于与计算结果比较，不考虑水分冻结时的冷缩段温度影响，直接认为未冻含水量的变化从初始冻结温度开始。

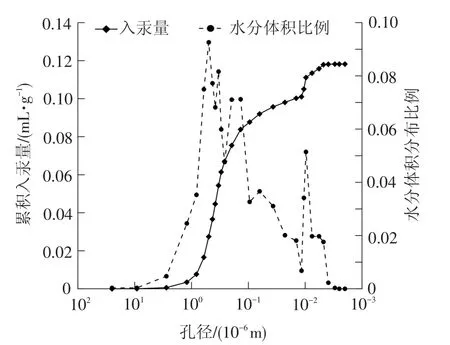
图2 粉质黏土孔径分布

取砂土试验值［2］、粉质黏土试验值［25］与模型计算值进行对比。对于粉质黏土，认为孔径分布与青藏高原粉质黏土一致，砂土颗粒参数与孔径关系见文献［19，26］，其未冻含水量与温度关系试验曲线见文献［2，27-28］。

2.1.2 计算与试验结果比较

依据式（23）和式（24），可计算不同土体在温度变化下的未冻含水量，其结果见图3。

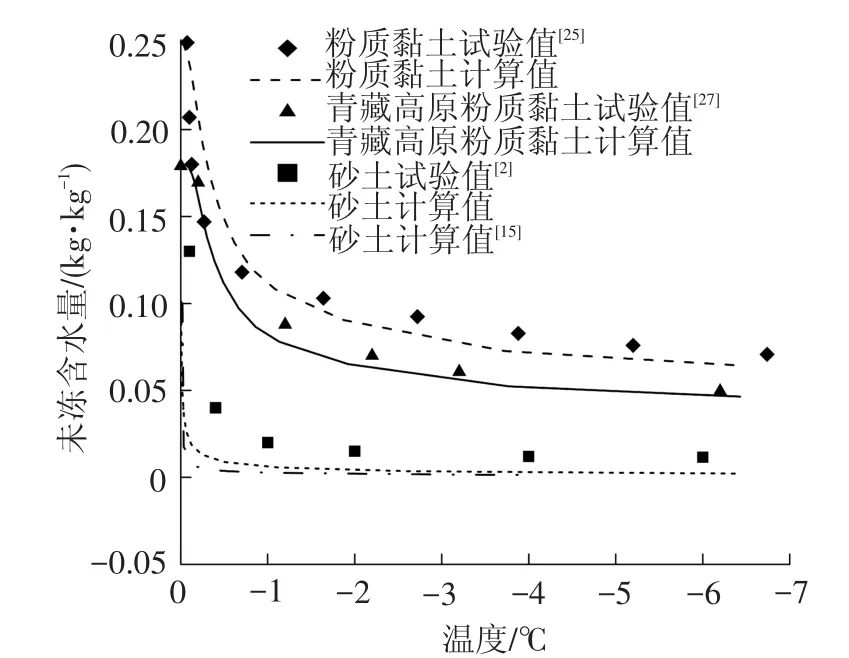
图3 不同土体未冻含水量与温度变化曲线

通过试验值与计算值对比可知，计算值比试验值略小，这是由于计算模型未考虑土颗粒对水分的吸附作用。对于砂土，由于制样很难保证饱和，而非饱和砂土中毛细力作用会一定程度上阻碍水分冻结，但与Dall’Amico计算模型相比，精度略微提高。所以，本模型计算式能够较好地模拟水分冻结过程，反映不同温度条件下未冻水含量多少。随初始含水量增加，未冻含水量曲线会向上微小移动。

2.2 水分传感器监测试验

水分传感器测试原理为时域反射法，是一种利用电磁脉冲方法，根据电磁波在土层中的传播速度，测试不同土层的介电常数，按介电常数值可获不同土类在冻结状态下的未冻水含量。

2.2.1 试验装置

基于自行设计的冻土水热特征试验箱展开未冻水变化规律测试［17］，该测试装置主要由控温系统（冷浴、冷浴液、制冷盘等）、测试系统（模型内箱、温度和水分测试传感器等）及数据采集系统构成，利用本装置可实现对试样的整体控温及快速冻融，能有效测量试样在冻融过程中的水热特征要素。模型内箱内部尺寸为0.40 m×0.30 m×0.30 m（长×宽×高），试验中采用的冷浴液为酒精，通过制冷盘实现测试试样的均匀控温，控温系统的温度范围为－40～50℃。测试系统中温度传感器精度为±0.05℃，水分传感器采用美国Decagon公司设计的5TM传感器（测试原理为FDR法，校准后体积未冻含水量测试精度±2%）。温度数据和体积未冻含水量数据同步采集。为便于对比，将监测得到的体积含水量转化为质量含水量。土样为青藏高原粉质黏土，初始含水量为23%，基本参数如上所述。

2.2.2 计算与试验结果比较

通过制冷降温可获得不同温度下的土体水分含量，室内监测数据与模型计算值结果对比见图4。

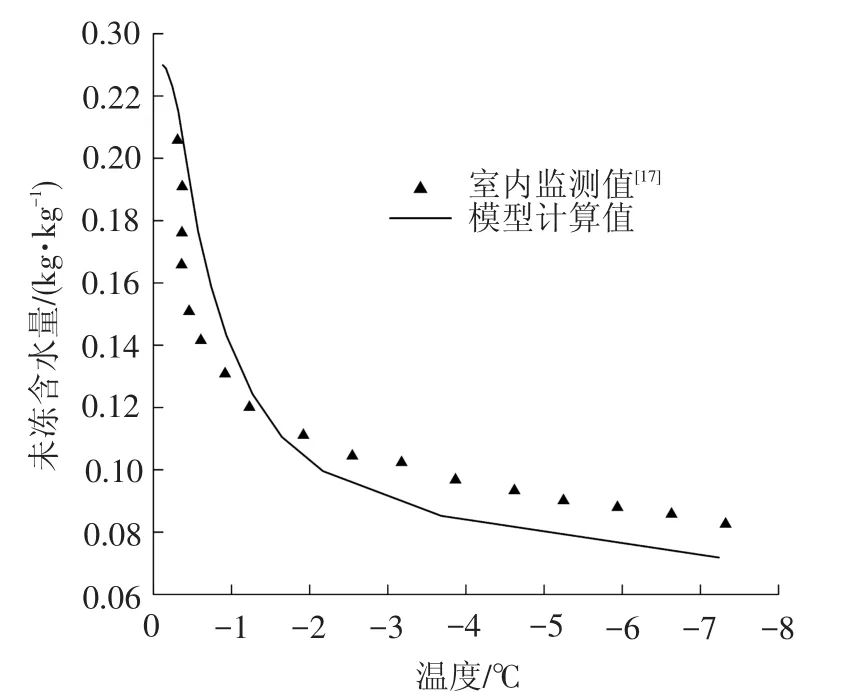
图4 室内监测数据与模型计算值结果对比

由图4可以看出，模型计算值能够较好地反应未冻含水量随温度变化，但由于水分传感器探头有一定尺寸，造成探测区域性较大，故存在一定误差，但整体上可反映水分冻结趋势。为了验证计算模型对天然冻土的适用性，采用试验段青藏高原楚玛尔天然场地地下1.5 m监测数据进行对比。水分监测仪器为5 T M传感器，该处土为亚黏土，故计算模型中孔径分布近似按图2进行计算，计算结果与监测结果对比见图5。

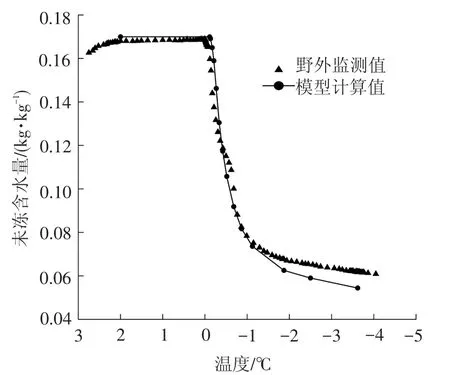
图5 计算结果与监测结果对比

由图5可见，计算模型能够较好地反映天然场地未冻含水量变化，但随着温度降低误差逐渐增大，由于天然场地水分随温度梯度会发生迁移，而计算模型中未考虑水分迁移。

为了研究孔隙特征对未冻含水量随温度变化的影响，假定初始含水量不变，通过孔径分布等比例减小或增大模拟不同土质下未冻含水量随温度变化规律。不同孔径下未冻含水量与温度变化的计算结果见图6。

由图6可以看出，当图6孔径减小时，水分冻结趋势减缓，当孔径增大时，水分冻结趋势加大。但当自由水完全冻结时，未冻含水量随温度降低变化非常缓慢，这时水分的冻结主要是部分结合水的冻结。

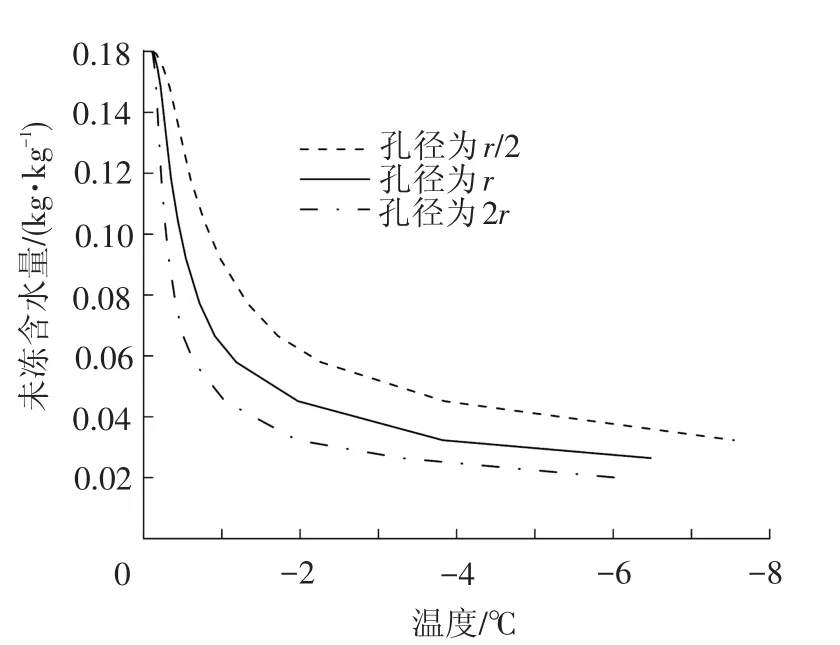
图6 不同孔径下未冻含水量随温度变化

3 讨论

公式推导过程中均采用绝对温度，若用摄氏温度表示只需要绝对温度减去273.15即可。式（23）、式（24）揭示了水分冻结规律，水分冻结先在大孔隙中发生，初始冻结温度由最大孔径决定。随着土体温度降低，较小孔隙中的水分开始冻结。对于饱和土体，若知道土体孔径分布，即可近似获取不同孔径中水分含量分布（将孔径分为若干区间，每个区间内均采用平均孔径计算）。不同孔径中水分冻结温度可依据式（23）计算，而未冻结含水量等于总含水量减去冻结含水量。由于小孔隙中水分冻结需要温度很低，故有一些小孔隙水很难冻结。在以上计算模型中，只考虑了自由水的冻结（认为孔隙中存在的全部是自由水），未考虑结合水的冻结。结合水受到土体颗粒的强吸附作用，在低温下很难冻结而以液态形式存在，故计算数值较试验数据较小。对于盐渍土，土体中含有一定数量的盐分，所以土中水是盐溶液。盐溶液的初始冻结温度较纯水低，具体可通过其水分活度计算初始冻结温度［27］。初始冻结温度的降低造成未冻含水量曲线向右移动，而移动的幅度主要取决于溶液中盐分浓度和离子类型。外界大气压或者外界荷载的变化也造成初始冻结温度的变化。当外界大气压变化时，水溶液和冰晶体共同受同样外界压力，式（8）可表示为

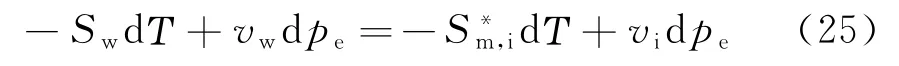
式中：pe为外界大气压变化或外荷载。

通过对式（25）积分，可得

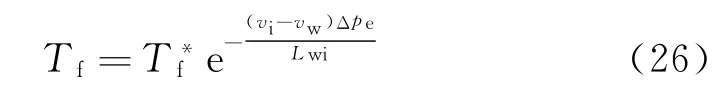
式中：Δpe为外界压力相对与标准大气压变化值。

从式（26）可以看出，当气压或外界压力增大时，冻结温度会降低。压力变化与冻结温度呈现反比例关系。通过计算可以发现，当标准大气压增大1 MPa时，土中水的初始冻结温度会降低0.073℃。其计算规律与徐学祖等［14］、张立新等［28］的研究结果一致。冻结温度的降低造成未冻含水量曲线向右侧移动。

同样含水量下，孔径越小的土，其未冻含水量随温度降低减少相对缓慢，而冻结初始时刻，未冻含水量变化规律基本趋于一致，温度越低，差距越明显。由图6可见，随着孔径减小，未冻含水量曲线发生逆时针旋转，而旋转幅度取决于土体颗粒粗细程度。为了研究冰晶对未冻含水量曲线影响，若不考虑冰晶对冻结温度的影响，可将式（23）变形为

比较式（23）和式（27）可以发现，考虑冰晶的作用使未冻水量曲线向右移动，即冰晶体的出现延缓了未冻含水量的冻结。

4 结论

基于冰水相变化学势相等，利用有效应力原理建立孔隙中冰水压力的关系，推导出未冻含水量与冻结温度的公式，并利用试验进行了验证，研究表明：

（1）水分冻结与土体孔径分布密切相关。土中水分冻结先从大孔径开始，随着孔径减小，孔隙中水分冻结难度增大。

（2）大气压或外荷载的增大、含盐量的增加导致未冻含水量与温度曲线向坐标右侧移动，而土中孔隙大小变化引起未冻含水量曲线旋转，若土颗粒变细，曲线逆时针旋转。

（3）孔隙中冰晶增加延缓水分冻结趋势，该现象随孔径的减小而愈发明显。

［1］赵其国，王浩清，顾国安.中国的冻土［J］.土壤学报，1993，30（4）：341-354.

ZH AO Qiguo，WANG Haoqing，GU Guoan.Gelisols of China［J］.Acta Pedologica Sinica，1993，30（4）：341-354.

［2］徐学祖，王家澄，张立新，等.土体的冻胀和盐胀机理［M］.北京：科学出版社，1995.

［3］陈肖柏，刘建坤，刘鸿绪，等.土的冻结作用与地基［M］.北京：科学出版社，2006.

［4］李宁，程国栋，徐学祖，等.冻土力学的研究进展与思考［J］.力学进展，2001，31（1）：95-102.

LI Ning，CHENG Guodong，XU Xuezu，et al.The Advance and Review on Frozen Soil Mechanics［J］.Advance in Mechanics，2001，31（1）：95-102.

［5］田亚护，沈宇鹏，隗新宇，等.多年冻土区路基U型水沟热力耦合理论分析及现场试验［J］.铁道学报，2015，37（7）：92-97.

TIAN Yahu，SHENG Yupeng，WEI Xinyu，et al.Theoretical Analysis of Thermo-mechanical Coupling and Field Test on U-type Canal of Embankment in Permafrost Regions［J］.Journal of the China Railway Society，2015，37（7）：92-97.

［6］张明礼，温智，薛珂，等.道砟层对多年冻土区铁路路基水热影响监测与分析［J］.铁道学报，2017，39（4）：94-100.

ZH ANG Mingli，WEN Zhi，XUE Ke，et al.Monitoring and Analysis of Impact of Ballast Layer on Thermal-moisture Dynamics in Railway Subgrade in Permafrost Regions［J］.Journal of the China Railway Society，2017，39（4）：94-100.

［7］BLACK P B.Application of the Clapeyron Equation to Water and Ice in Porous Media［R］.U.S.Army Corps of Engineers：Cold Regions Research and Engineering Lab，1995.

［8］MA W，ZH ANG L，YANG C.Discussion of the Applicability of the Generalized Clausius-Clapeyron Equation and the Frozen Fringe Process［J］.Earth-Science Reviews，2015，142：47-59.

［9］KUJALA K.Unfrozen Water Content of Finnish Soils Measured by NMR ［C］／／International Symposium on Frost in Geotechnical Engineering.Rathmayer H.Espoo，Finland，1989：301-310.

［10］黄兴法，曾德超，练国平.土壤水热盐运动模型的建立与初步验证［J］.农业工程学报，1997，13（3）：32-36.

HUANG Xingfa，ZENG Dechao，LIAN Guoping.A Numerical Model for Coupling Movement of Water Heat and Salt in Soil under the Conditions of Frozen，Unfrozen，Saturated and Unsaturated［J］.Transactions of the CSAE，1997，13（3）：32-36.

［11］SHENG D，AXELSSON K，KNUTSSON S.Frost Heave Due to Ice Lens Formation in Freezing Soils 1：Theory and Verification［J］.Nordic Hydrology，1995，26（2）：125-146.

［12］马巍，王大雁.冻土力学［M］.北京：科学出版社，2014.

［13］万旭升，赖远明，廖梦柯.硫酸盐渍土未相变含水量与温度关系研究［J］.岩土工程学报，2015，37（12），2175-2181.

WAN Xusheng，LAI Yuanming，LIAO Mengke.Study on Relationship between Water Content of Sodium Saline Soil without Phase Transformation and Temperature［J］.Chinese Journal of Geotechnical Engineering，2015，37（12），2175-2181.

［14］徐学祖，王家澄，张立新，等.冻土物理学［M］.北京：科学出版社，2010.

［15］DALL’AMICO M，ENDRIZZI S，GRUBBER S，et al.A Robust and Energy-conserving Model of Freezing Variably-saturated Soil［J］.The Cryosphere，2011，5（2）：469-484.

［16］朱定一，廖选茂，戴品强.反应型固液界面能的理论表征与计算［J］.科学通报，2013，58（2）：181-187.

ZHU Dingyi，LIAO Xuanmao，DAI Pinqiang.Theoretical Analysis of Reactive Solid-liquid Interfacial Energies［J］.Chinese Science Bulletin，2013，58（2）：181-187.

［17］裴万胜.冻土水-热-力相互作用过程及数值模拟研究［D］.兰州：中国科学院大学，2015.

［18］HILLING W B.Measurement of Interfacial Free Energy for Ice／Water System［J］.Journal of Crystal Growth，1998，183（3）：463-468.

［19］胡凯，赖远明.含盐冻结粉质砂土的强度参数和强度准则试验研究［J］.冰川冻土，2014，36（5）：1199-1204.

HU Kai，LAI Yuanming.Experimental Study on the Strength Parameters and Strength Criteria of Saline Frozen Silty Sand［J］.Journal of Glaciology and Geocryology，2014，36（5）：1199-1204.

［20］付献彩，沈文霞，姚天扬，等.物理化学［M］.北京：高等教育出版社，2005.

［21］O＇NEILL K，MILLER R D.Exploration of a Rigid Ice Model of Frost Heave［J］.Water Resources Research，1985，21（3）：281-296.

［22］CHEN F X，LI N，CHEN G D.The Theoretical Frame of Multi-Phase Porous Medium for the Freezing Soil［J］.Chinese Journal of Geotechnical Engineering，2002，24（2）：213-217.

［23］ZHOU J Z，LI D Q.Numerical Analysis of Coupled Water，Heat and Stress in Saturated Freezing Soil［J］.Cold Region Science and Technology，2012，72：43-49.

［24］炳慧，马巍.盐渍土冻结温度的试验研究［J］.冰川冻土，2011，33（5）：1106-1113.

BING Hui，MA Wei.Experimental Study on Freezing Point of Saline Soil［J］.Journal of Glaciology and Geocryology，2011，33（5）：1106-1113.

［25］冷毅飞，张喜发，杨凤学，等.冻土未冻水含量的量热法试验研究［J］.岩土力学，2010，31（12）：3758-3764.

LENG Yifei，ZH ANG Xifa，YANG Fengxue，et al.Experimental Research on Unfrozen Water Content of Frozen Soils by Calorimetry［J］.Rock and Soil Mechanics，2010，31（12）：3758-3764.

［26］EVERETT D H.The Thermodynamics of Frost Damage to Porous Solids［J］.Transactions of the Faraday Society，1961，57（5）：1541-1551.

［27］WAN X S，LAI Y M，WANG C.Experimental Study on the Freezing Temperatures of Saline Silty Soils［J］.Permafrost and Periglacial Processes，2015，26（2）：175-187.

［28］张立新，徐学祖，张招祥，等.冻土未冻含水量与压力关系的实验研究［J］.冰川冻土，1998，20（2）：124-127.

ZHANG Lixing，XU Xuezu，ZH ANG Zhaoxiang，et al.Experimental Study of the Relationship between the Unfrozen Water Content of Frozen Soil and Pressure［J］.Journal of Glaciology and Geocryology，1998，20（2）：124-127.