变电站风险评价机制中图论思想的体现

杨迪

摘要：不同电压等级间的联络枢纽是变电站，其在不同电压等级能量交换方面起着重要的作用，评估变电站主接线渐渐变为研究热点。首先，变电站风险评估使用图论可达矩阵识别连通性的方法.-f转化为变电站内部负荷点和电源点的连通性识别问题；其次，对变电站是否失荷进行判断；最后，对风险理论进行结合计算变电站风险。算例的仿真结果可以对此方法的有效性和正确性进行表明。

关键词：应用 图论 风险评价机制 变电站

在电网中起枢纽作用的为变电站，供电的可靠性与稳定安全运行对变电站关系重大。变电站按功能可分解为电源和负荷两部分，变电站的抗风险能力可由这两部分的连通度映射。割集理论法和直接标号法是变电站内部主接线连通评价的主要方法。直接标号法对复杂接线状况难于处理；割集法可以多电源点多负荷点的连通评估进行解决，但是过程比较繁琐。现如今没考虑随机因素的影响是研究的大不足。本文将对基于图论的变电站风险评估体系进行完善，以此使变电运行管理水平提升。

一、变电站连通性分析

（一）变电站的邻接矩阵

变电站内部连通性识别的基础是变电件邻接矩阵的形成。变电站内部电气主接线能够抽象为点，边关系图G（V，E），电气节点集合为点集V={V₁，V₂，…，V_n），包括站內的母线和设备连接点；站内的支路和断路器集合称为边集E={e₁，e₂，…，e₁）。顶点V_i与和V_j间边数用a_ij表示，可能取0，1，2，图G的邻接矩阵为矩阵A=A（G）=（a_ij）nn。反映出任意两个节点间连通性使邻接矩阵的物理意义，个n节点数的图，随意两个节点最多能通过其他n-2个节点连通。一般变电站的任一节点与其他节点联系较少，所以邻接矩阵A有很高的稀疏性，并具有对称性。

（二）变电站的可达矩阵

通过逻辑运算在确定了变电站邻接矩阵的基础上获得可达矩阵，对变电站的连通性进行识别R=（r_ij）nn。定义图G的可达矩阵为矩阵R=（r_ij）nn。

可达矩阵采用邻接矩阵自乘法计算时，对n节点数的图，邻接矩阵A是个nn的矩阵，i、j为一级连通时，i、j间直接连通，a_ij=1；i、j为二级连通时，通过节点k，i、j才能连通。对可达矩阵R的求解步骤如下：（1）根据变电站站内电气主接线抽象成变电站的图G；（2）邻接矩阵A（G）由变电站图G的连接信息形成；（3）依据式对可达矩阵求取。节点i、j之间的连通紧密程度关系可由r_ij数值的大小表示，数值越大，连通越紧密。

二、变电站风险评估模型

（一）变电站系统状态选取

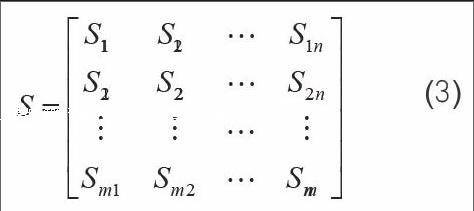
在对变电站风险进行评估时，对变电站因内部元件随机退出运行产生的影响进行考虑是合理的。计算机产生随机数对n个元件的变电站进行抽样，产生了m个不同的状态，表达式为：

元件的状态为S_ij，工作和失效是元件的两个状态，所有元件失效相互独立。经由计算机产生的在[0，1]之间的均匀随机数R_i来对元件的状态模拟。

（二）变电站连通性识别及风险指标计算

由MonteCarlo模拟法产生的任一个变电站系统状态，都对对应变电站邻接矩阵A进行修改，并对任个变电站系统状态通过逻辑运算获得可达矩阵R。对变电站风险采用失负荷量EENS和失负荷概率PLC两个风险指标进行评估。

计算公式为：

式中EENS_k和PLC_k分别为节点k失负荷风险和失负荷概率：EENS为变电站失负荷风险。

三、算例分析

根据分析前面的理论，以IEEE-RTS79系统为例，计算节点9、10、11和12所组成的变电站风险。为使变电站主接线得到合适的选取，对两种不同的主接线方式下变电站的风险进行了算例对比分析。第种是变电站接线方式（以下称方案A），第二种是文章改进的变电站接线方式（以下称方案B）。

对这两种主接线方式而言，先是抽象母线，开关描述的物理模型为节点，支路描述的图G，再对变电站失负荷指标结果进行计算。变电站每个PLC_K是该负荷点所有可能发生失负荷状态的概率之和，每个EENS_K指标是所有可能失负荷量状态相加得到的总和。运行人员关注的是个变电站的风险。所以，本文中对EENS和PLC进行了计算。看A、B两种主接线风险指标结果得：（1）方案B相较于A，减小了4.9%的电站负荷削减概率指标，减小了6.1%的期望缺供电量指标，这是由于方案B相较于A的网络联络性较强。两个不同负荷节点的负荷总量不同导致方案A、B中两个对称负荷节点的EENS指标不同。（2）对方案A和B进行对比可得，变电站每个节点的风险指标因变电站主接线的不同而不同，每个节点的风险指标大小会发生变化，但方案B在整个变电站的风险指标上比方案A的风险小。

四、结语

变电站风险评估使用图论可达矩阵识别连通性的方法可转化为变电站内部负荷点和电源点的连通性识别问题，变电运行管理水平因为完善基于图论的变电站风险评估体系而得到提高，从而使本文改进的变电站接线方式在整个变电站的风险指标上比变电站接线方式小。endprint