高斯仿射DTSM的HW估计方法与小样本偏差修正
王雪标,王 晰,赵前程
(1.东北财经大学 a.数学学院,b.经济学院,辽宁 大连116025;2.大连海洋大学 经济管理学院,辽宁 大连116025)
一、引 言
高斯仿射动态期限结构模型(DTSM)是在无套利框架下研究不同期限的收益之间的关系,最具代表性的模型包括Vasicek、Duffie、Dai和Duffee等研究中使用的模型[1-4],它们已成为基本且有力的宏观金融工具。高斯仿射DTSM的最大优势在于更容易估计市场风险价格,所以在无套利的假定下,可以预测资产的价格。如Duffee等估计了利率风险溢价[4];Ang等研究了宏观经济发展和货币政策如何影响利率期限结构[5];Rudebusch和Bekaert等描述了货币政策规则[6-7];Christensen从名义利率和通胀指数债券的价差中推断了市场通胀预期[8]。
高斯仿射DTSM的最新估计方法包括Joslin、Singleton和Zhu的方法(JSZ)[9]、Hamilton和Wu(HW)估计方法等[10]。Hamilton和Wu研究了短期利率是0下限时,货币政策影响利率的潜力,评价了中央银行在金融危机期间干预的有效性。但是,在估计必要参数时上述文献都面临着巨大的挑战,其原因是非线性和似然表面平坦问题,如Kim提到,无套利模型灵活的表达形式引起大量的参数需要估计,参数之间的非线性关系及必须进行的非线性优化都使估计变得异常困难[11]。Ang等同样认为,当收益持久性较高时,用极大似然估计去估计一个很多因子的模型非常困难,需要更好的初始值才能收敛,而决定长期收益均值的似然表面过于平坦,将不利于得到全局最优解[5]。
针对上述问题,Hamilton和Wu在2012年提出了解决方法,其表达式被称为“简约形式”,其模型也简称为HW模型:对一般的高斯仿射类期限结构模型,假定有N个不可观测的定价因子,可观测的收益或者宏观变量可以被N个因子精确定价,模型的参数可以用简约形式直接估计,如OLS,虽然在简约参数计算中包含了解析法和数学运算,但数学计算成份远比极大似然方法找到极大值简单,对于恰好刚能识别的结构,相对于必须试大量的初值,也依然不能保证得到全局最优解。然而,数学计算有额外的优势,研究者可以知道方程是否已经得解,也可以确切地知道是全局最优还是局部最优解。通过Hamilton和Wu提出的最小卡方估计(MCSE),对简约形式加入过度识别限制后仍能像无限制简约形式一样估计结构参数。HW估计方法证明了MCSE方法可以避免很多MLE估计高斯仿射期限结构模型所带来的数学问题,其中也包括计算小样本标准差和置信区间上的优势,Hamilton和Wu的实证结果也说明Ang和Piazzesi所得的解是似然表面的局部最大,其解为局部最优,而不是全局最优[5,10]。
HW的估计方法可以用于任何形式的DTSM,JSZ模型的参数化的第一步实际上与HW的简约形式一致,也是利用全部信息的MLE,可以通过OLS的方法获得,然而使用JSZ方法估计其余的参数仍需要利用MLE方法,而不同于HW估计方法。JSZ方法在存在单位根的情况下不可识别,另外在遇到高度持续性的数据时,会遇到与早期的DTSM估计使用MLE类似的问题,而HW的估计方法可以避免这个问题。
二、HW估计方法的基本框架
HW方法以最小卡方估计取代极大似然估计,此方法可以提高估计的效率,并且更容易判断其结果是否为全局最优解。本文将实证分析HW模型中存在的偏差及探讨小样本偏差对过度识别限制的影响。
HW估计方法是对高期仿射DTSM的求解方法,模型的描述、风险价格、定价核与传统的高斯仿射DTSM、JSZ估计方法没有本质的区别,其简述如下:
考虑一个M维向量Xt,其动态过程可以用高斯向量自回归描述:
Xt+1=μ+ΦXt+∑εt+1
(1)
其中,εt~i.i.d.N(0,IM)。用rt表示无风险单期利率,Mt,t+1表示定价核,使用仿射期限结构使用的一般的定价核:
(2)
其中,λt是M×1向量,描述投资者对风险的态度,风险中性情况下其值为0。
仿射期限结构模型中风险的市场价格本身也是因子Xt的仿射函数:
λt=λ0+λ1Xt
(3)
这里λ0是一个M×1向量,而λ1是M×M矩阵,同样风险中性情况下:
μQ=μ-Σλ0
(4)
ΦQ=Φ-Σλ1
(5)
换句话说,风险规避投资者评价资产和风险中性投资者是一样的,因子也是用Q测度的VAR描述:
(6)
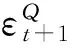
(7)
无风险n期纯折现债券的收益计算方法为:
(8)
其中:
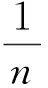
(9)

(10)
若已知μQ、ΦQ、δ0、δ1、Σ,可以利用式(8)、(9)、(10)预测各期限n的收益。
从以上论述可知,仿射期限结构模型中有三套参数集:P测度参数集:μ、Φ、Σ用于描述因子的动态性;参数λ0、λ1用于描述风险的价格;Q测度参数μQ、ΦQ,这三套参数集已知其中的两套,可以求得第三套。
假定需描述nd个不同期限的收益,nd大于n,n是定价因子的个数,虽然可以通过一些收益预测另一些收益,但拟合往往不准确,此时一般会用Ang和Piazzesi、Wei的卡尔曼滤波[5]、Chen和Scott的方法[12],假定n可观测收益的线性组合对于式(8)精确成立,而其余的ne=nd-n带有测量误差。用表示(n×1)个向量构成的收益的线性组合是无误差精确定价的是其余的(ne×1)个向量构成的收益的线性组合,其带有误差,则两者可用式(11)表达:
(11)
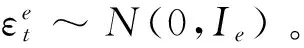
Dai、Duffee、Kim等将因子Xt视为可观测的[3-4,11],因此在式(11)中也如此处理,因子的数量n一般为3,即不带误差的可观测的收益数量为3,这三个因子可以是潜在的,用NS模型得到水平因子、斜率因子和曲率因子或其代理,也可以为收益主成分分析得到的前三个主成分。这三个因子还可以选择三个有代表性的收益,如Ang等用1月、12月和60月期限的收益代表这三个因子[5],期限为36月的收益代表即带误差的一项,这样式(11)表示为:
(12)
其中的an、bn可用式(9)和式(10)得到。
Dai和Singleton提出的标准化的条件是Σ=IN,δ1≥0,μ=0,Φ是下三角阵[3];对Q测度下的参数进行了类似的限制Σ=IN,δ1≥0,μQ=0,ΦQ是下三角阵;HW模型的限制为Σ=IN,δ1≥0,μ=0,ΦQ为下三角阵。对于N=3,Ne=1 的情况,式(12)有23个未知参数,其中μQ里有3个,ΦQ里有6个,Φ里有9个,δ0里有 1个,δ1里有3个,Σe里有1个,因此参数向量θ为(23×1),似然函数为:

logφ(Xt;μ+ΦXt-1,IN)+
(13)
其中的φ是多元正态密度函数。其他几个变量为:
(14)
(15)
(16)
其中,Chen-Scott的求解方法就是最大化式(13)[12]。Hamilton和Wu进行了模拟实验,使用matlab的fminunc算法寻找式(13)的最大值,100次实验中只有一次得到了全局最优解,81次满足收敛条件但退出时得到的是局部最优,另有18次因初始值的原因得不到结果,优化算法没有任何进展[10]。因此,通过传统的估计方法得到真正的全局最优解是非常困难的。
三、HW估计模型的识别、估计过程与实证
(一)HW估计模型的识别
前文已设置了标准化条件为Σ=IN,μ=0在此条件下将式(1)两端乘以B1,结果为:
(17)

(18)
(19)
(20)
同样地,根据式(11)还可得到:
(21)
(22)
(23)
(24)
(25)
(26)
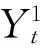
(二)HW的估计过程
HW估计方法中,简约形式的极大似然参数估计仍然很繁琐,比较可行的做法是用OLS代替极大似然估计,Hamilton等提出用最小卡方估计代替极大似然估计的做法[10],下面简述其主要原理:

(27)
θ是个已知向量参数,可以通过Wald统计量检测π=g(θ):
(28)
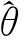
(29)
Γ=∂g(θ)/∂θ′|θ=θ0
(30)
γ=g(θ0)-Γθ0
(31)

(32)

对于一个刚好识别的模型,式(32)可以实现的最小值是0,这种情况下可以简化为最小化式:
(33)
在Ne=1的情况下,只有潜在因子的仿射模型刚好识别,应用最小卡方估计极有吸引力,简约形式的参数向量为:

在道路桥梁路线设计阶段,设计单位应该综合自身掌握的地形地质条件、周边自然环境资料等对工程投入运营后可能会出现的问题进行分析预测,在此基础上制定科学合理的维护养护和检测维护计划,促进道路桥梁工程使用寿命的提升。
(34)

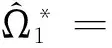
(35)
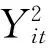
潜在因子模型在N=3,Ne=1的情况下,可以通过最小化式(33)完成模型求解,过程如下:
2.通过解式(23)和式(25)中的方程求解ΦQ、δ1中的9个参数。由于:
(36)
(37)
特别地,通过设置:
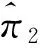
(38)

(39)
3.解析从式(20)中获得的Φ。
(40)

4.通过数学方法求解δ0、μQ中的4个参数,使用式(19)、式(22)中的方程:
(41)
(42)
虽然第二步到第四步包含了数学最小化,但相比传统的似然函数关于参数θ的最大化简单得多。使用传统方法,100个不同的初值实验只有1次收敛到全局最优,而HW的实验表明了其稳健性,使用HW方法,100次都得到了全局最优解,稳健的原因主要是相比传统的方法在搜索Φ解时,HW用解析法避免了其不确定性。
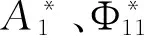
(三)HW估计方法对中国利率期限结构实证

(43)
其中的an、bn仍用式(9)和式(10)得到。估计的结果如表1所示。

表1 HW方法估计中国利率期限结构实证结果
四、 HW估计方法的小样本偏差修正与实证
以下将论述基于HW估计方法研究高斯仿射DTSM的小样本偏差修正。首先,介绍HW估计方法小样本偏差修正过程,然后对HW估计方法的小样本偏差修正进行实证,在实证过程中探讨小样本偏差修正对施加过度识别限制的DTSM模型估计的影响,比较偏差修正前后的结果。修正的核心技术仍是Bootstrap方法。
(一)HW估计的小样本偏差修正方法
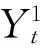
(44)
(45)

正如上文所介绍,HW通过两个步骤估计DTSM,第一步采用OLS方法估计简约形式VAR,第二步的结构模型参数通过最小卡方估计获得。对于偏差修正估计,将第一步的OLS估计用偏差修正估计代替;而对第二步的同期回归方程,由于OLS是无偏的,没有必要进行偏差修正。这里只是第一步通过偏差修正获取参数,第二步同上文的HW做法一致,二者都是使用最小卡方统计。为了获取偏差修正估计的标准差,主要采用HW的渐近近似法,只是在相关公式中加入了偏差修正的点估计。
(二)HW估计的小样本偏差修正实证
下面对HW估计方法小样本偏差修正进行实证,并在实证过程中探讨小样本偏差修正对施加过度识别限制的DTSM模型估计的影响。
前人的研究中,大多动态期限结构模型都施加了过度识别的参数限制,有的施加于动态系统,如Ang和Piazzesi[5],Kim和Orphanides[11];或者施加于Q测度参数,如Christensen[8];或施加于风险敏感性参数λ0、λ1。在这些限制下,大多文献都是利用横截面信息帮助确定VAR参数,也有研究是利用无套利假定帮助解决小样本偏差和统计不确定性问题,如Cochrane和Piazzesi[14],Joslin、Priebsch和Singleton[9]。本文考虑对限制的DTSM使用HW估计方法进行估计,并评价小样本偏差修正对模型估计的影响。本文主要讨论风险价格上增加限制,参考Bauer、Rudebusch和Wu的方法[15]。
本文选取与上文相同的数据,其中银行间国债即期收益率数据,同样使用每月月末的数据,数据来源于万德(wind)数据库,到期期限为1、2、3、5、7和10年,时间范围为2006年3月到2015年9月。
施加的限制参考Bauer、Rudebusch和Wu的方法[15],首先估计一个没有偏差修正的最大灵活性的模型,参数估计和标准差的获取同HW一样,这种估计方法称为OLS-UR;其次把Σλ1中的t统计量小于1的四个元素设置为0,这意味着不考虑参数的联合显著性和模型的不确定性,这是DTSM模型增加限制的通常做法之一,如Bauer提出一个框架系统处理DTSM模型的选择和模型的不确定性问题,也采用了这种限制方法[16];最后对增加了限制后的模型分别采用两种估计方法,一种不加小样本偏差修正,称为“OLS-R”,另一种利用小样本偏差修正,称为“BC-R”。
表2报告了参数估计的结果,其中括号内的数值为估计的标准差,Q测度下三种估计的结果非常接近,主要原因是这些参数主要收益的横截面是由数据确定的,基本上不受限制的影响,然而风险价格参数OLS-R与BC-R是不同的。很显然,这种施加限制的模型,对风险敏感性的估计有显著的影响。

表2 过度识别限制偏差修正前后的估计结果
借鉴上文的方法,再次分解5到10年的远期利率为风险中性利率和期限溢价成份,图1和图2比较了在三种估计下的风险中性利率和期限溢价。图1是风险中性远期利率比较,图2是远期期限溢价的比较。
表3同样给出了三种估计下的相关统计量。从表3可以看出,施加过度识别限制后,对持续性有影响,但效果并不明显,OLS-R与OLS-UR最大的特征根分别为0.990 4和0.990 6,二者相差较小,增加限制而不进行小样本偏差修正使风险中性远期利率波动略有增加,从0.000 3增加到0.000 7,而远期期限溢价波动略有减小,从0.004 4减小到0.004 2。总之,加入4个0限制在Σλ1上对模型的经济意义影响不大,而偏差修正后的DTSM模型的估计具有重要的经济意义,施加限制后经过小样本偏差修正后的BC-R的持续性增加比较显著,从表3可以看出,半衰期修正前是12,而修正后达到了18,风险中性远期利率波动由0.000 7变为0.001 8,也可以从图1中看出这一波动明显增加。但是,远期期限溢价波动OLS-R与OLS-UR相比基本不变,波动都约为0.004 2,从图2中也可看出其变化不大。总之,传统的DTSM估计中远期利率变化主要归因于期限溢价,而偏差修正估计显示主要归因于风险中性利率,因此政策预期在本研究问题中起了非常重要的作用。

表3 施加过度识别限制前后相关统计量

图1三种估计下远期风险中性利率图

图2 三种估计下远期期限溢价图
五、结 论
HW估计方法是现代高斯仿射期限结构模型估计中较为全面的方法,两步估计都是OLS估计,优化过程以最小卡方估计代替了极大似然估计,不存在极大似然估计经常存在的局部最优解问题及初值依赖性问题。
本文借鉴HW估计方法,将高斯仿射DTSM表示成一种“简化形式”,用最小卡方估计方法代替极大似然估计法,此估计方法渐近等价于极大似然估计,但可以更快判断其结果是全局最优还是局部最优,克服了前人通过施加任意限制来获得估计值,或者在某些情况下没有得到真正的似然函数的全局最优解的问题,因此本文基于Bootstrap方法对HW模型进行小样本偏差修正。HW估计方法的第一步通过OLS估计简约形式VAR,因此可以用Bootstrap偏差修正估计代替;第二步的结构模型参数是通过最小卡方估计获得,这一步的估计是无偏的,不需要修正。运用修正后的HW估计方法来探讨施加过度识别限制后的风险中性远期利率和期限溢价的变化。实证结果发现,如果不进行小样本偏差修正,施加过度识别限制并没有对系统产生显著的影响,经过小样本偏差修正后,系统显示了显著的持续性特征,风险中性远期利率波动也增加了很大,说明HW估计方法低估了系统的持续性风险中性远期利率的波动性。
[1] Vasicek O.An Equilibrium Characterization of the Term Structure[J].Journal of Financial and Quantitative Analysis,1977,5(4).
[2] Duffie D,Kan R.A Yield-Factor Model of Interest Rates[J].Mathematical Finance,1996,6(4).
[3] Dai Q,Singleton K J.Fixed Income Pricing[J].Handbook of the Economics of Finance,2002,1(3).
[4] Duffee G R.Term Premia and Interest Rate Forecasts in Affine Models[J].The Journal of Finance,2002,57(1).
[5] Ang A,Piazzesi M,Wei M.What Does the Yield Curve Tell Us about GDP Growth?[J].Journal of Econometrics,2006,131(1-2).
[6] Rudebusch G D,Wu T.A Macro-Finance Model of the Term Structure,Monetary Policy and the Economy[J].The Economic Journal,2008,118(530).
[7] Bekaert G,Cho S,Moreno A.New Keynesian Macroeconomics and the Term Structure[J].Journal of Money,Credit and Banking,2010,42(1).
[8] Christensen J H E.The Affine Arbitrage-Free Class of Nelson-Siegel Term Structure Models[J].Journal of Econometrics,2011,164(1).
[9] Joslin S,Priebsch M,Singleton K J.Risk Premiums in Dynamic Term Structure Models with Unspanned Macro Risks[J].The Journal of Finance,2014,69(3).
[10] Hamilton J D,Wu J C.Identification and Estimation of Gaussian Affine Term Structure Models[J].Journal of Econometrics,2012,168(2).
[11] Kim D H,Orphanides A.Term Structure Estimation with Survey Data on Interest Rate Forecasts[J].Journal of Financial and Quantitative Analysis,2012,47(1).
[12] Chen R R,Scott L.Maximum Likelihood Estimation for a Multifactor Equilirium Model of the Term Structure of Interest Rates[J].Journal of Fixed Income,1993,3(3).
[13] Rothenberg M.A New Inverse-Filtering Technique for Deriving the Glottal Air Flow Waveform during Voicing[J].Journal of the Acoustical Society of America,1973,53(6).
[14] Cochrane J H,Piazzesi M.Decomposing the Yield Curve[J].Social Science Electronic Publishing,2009(35).
[15] Bauer Michael D,Rudebusch Glenn D,Wu Jing Cynthia.Correcting Estimation Bias in Dynamic Term Structure Models[J].Journal of Business & Economic Statistics,2012,30(3).
[16] Bauer M D.Bayesian Estimation of Dynamic Term Structure Models under Restrictions on Risk Pricing[R].Federal Reserve Bank of San Francisco Working Paper Series,2014.

