追踪导引法的MATLAB仿真实现

孙浩轩

摘 要 随着军事科技的发展，导弹凭借其精确性和杀伤性备受重视，对于精确制导技术的研究越来越多，而导引法作为精确制导的基础更为重要。本文基于对导弹和目标的相对运动关系的分析，研究了追踪导引法的相对运动方程，并利用MATLAB实现了追踪法的仿真实验。

关键词 追踪法；相对运动方程；MATLAB仿真

中图分类号 TP3 文献标识码 A 文章编号 1674-6708（2018）202-0141-03

1 背景

随着科学技术的不断发展，各种高技术武器被运用在信息化战争中，例如各种精确制导武器，雷达无法发现的隐身战机舰船，还有人工智能控制的高度电子化武器，甚至还出现了通过发射激光来摧毁目标的新式激光武器。其中制导导弹更是在多次战争中屡建奇功。例如在海湾战争中，美国军队的 “爱国者”导弹成功拦截了伊拉克发射的大量飞毛腿导弹，而这也使得中国军队领导人见识并认识到导弹在现代战争中所能够发挥出的巨大作用。

随着科技的不断进步各国的军事实力也随之不断增强，这导致在现代的战争中两方军队直接面对面作战的几率大大降低，所需要打击的目标往往是位于几十，几百甚至是几千米以外的地面或水上目标或者是在高空快速运动的飞行器等等，具有很高的瞄准难度，而这就要求在现代战争中所应用的武器要具有更远的有效打击距离，更高的精准度及更大的杀伤范围。由于导弹具有射程远、威力大、精度高、速度快的特征很好的满足了现代战争的要求，所以在近代战争如第四次第五次中东战争、两伊战争，英阿在福克兰群岛的海空大战，都是以导弹主导的现代化战争。

为了使导弹能够在最短时间内有效的打击目标，各国都在对制导方式进行不断的探索。现在的主流导引方法主要有以下4种。

1）追踪法。作为最早提出的导引法，追踪法的原理是控制导弹轴向一直都指向其打击目标。2）三点法。三点法导引原理是遥控导弹沿指导站、导弹和目标所在的直线飞行，是遥控制导体系中主要的导引律，也经常被应用于复合制导中。 3）平行接近法。在导弹飞行中，控制弹目视线角速度为零，这一导引方法即为平行接近法。4）比例导引法。比例导引法的研究是为了弥补其他导引法的不足，它是通过控制导弹运动的速度方向角变化的角速度与弹目视线角变化的角速度成比例来进行制导的，这一比值通常称为导航比。导航比的取值不同，便是不同的导引法，当取1时，就是追踪法，当取为正无穷大时，就是理想状态下的平行接近法，但通常导航比取值2～6，这时便是比例导引法。本文主要研究较为基础的追踪法，并通过数学仿真加以实现。

2 追踪法

列出相对运动方程是研究导引规律最常用的基础方法，它是根据目标、导弹、制导站三者之间的相对运动关系所建立的方程组。

如图1所示，T表示攻击目标，M表示导弹，目标与导弹之间的连线为视线。再任意选择出一参考线Ax，为了使运动方程简单起见一般选择目标所在平面中的水平直线为参考線。

通过对式（4）直接积分可以得到导弹攻击目标的弹道，直接求解这个方程比较麻烦，所以本文利用MATLAB这一数学工具编写相应的程序，调用龙格-库塔法ode45直接求解相对运动方程组。

3 制导算法设计

3.1 龙格-库塔法简要介绍

在求解微分方程时，龙格-库塔法（RungeKutta methods）是十分常用且有效地方法之一。龙格-库塔法是在工程上得到了广泛应用，数学软件MTLAB中就集成了这一方法并以函数的形式可以被调用，其中ode45是较为基础也是广泛运用的函数。

3.2 MATLAB仿真实验

假设原点为导弹出发点，目标做匀速直线运动，速度方向为水平方向，大小为600m/s；导弹的速度始终为750m/s；初始时刻，目标位于导弹的正上方，距离为1 000m。利用MATLAB进行编程，程序框图如2所示，具体的MATLAB程序见附录。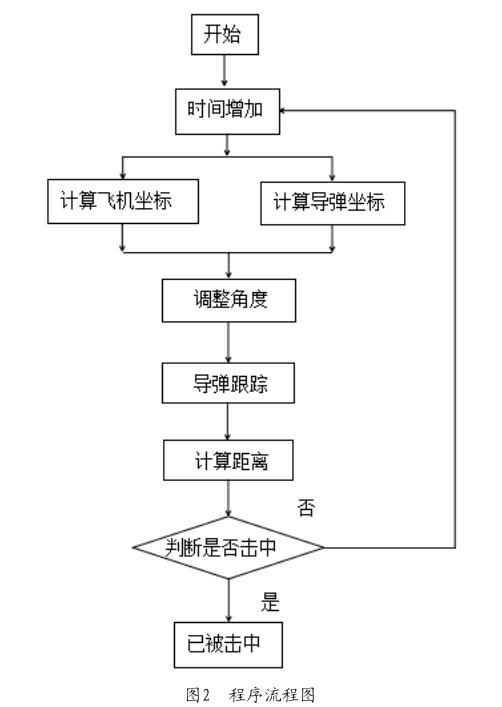

假设击中目标为导弹与目标之间的相对距离等于零。运行MATLAB程序后，可以的得到如图3所示的导弹追击目标的轨迹以及如图4所示的导弹和目标的相对距离随时间的变化曲线。在图3中，红色直线表示的是目标的运动轨迹，符合其作匀速直线运动的运动状态，蓝色曲线表示的是导弹的运动轨迹，弯曲度较大。通过图4的相对距离变化曲线，可以看出约3.7s后导弹击中了目标，此时导弹和目标的相对距离为零。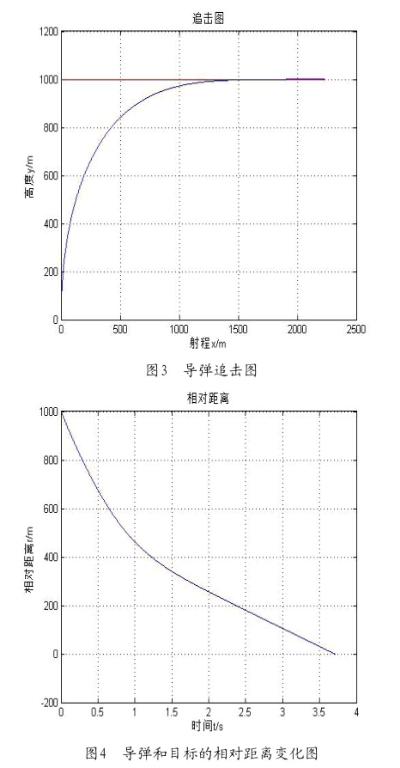

3.3 总结

通过以上的研究和数学仿真可以看出，作为一种基础导引法，追踪法能够较为快速的追击目标，但是随着与目标的距离越来越小，导弹的弹道会变得十分弯曲，到后期，导弹只能在目标后方追击，这就限制了追踪法对运动复杂的目标进行追击，也对导弹的过载能力有了更大的要求。这也是人们转而研究比例导引法和平行接近法的原因之一。

参考文献

[1]钱杏芳，林瑞雄，赵亚男.导弹飞行力学[M].北京：北京理工大学出版社，2008.

[2]陈涛.导弹平面制导算法设计[D].沈阳：沈阳理工大学，2009.

[3]刘卫国.MATLAB程序设计教程[M].北京：中国水利水电出版社，2005.