应变疲劳试验中小梁刚度损伤模型研究

丁 彪，郑传超，彭子馨，陈团结

(1.中交第一公路勘察设计研究院有限公司，陕西 西安 710075；2.长安大学 公路学院，陕西 西安 710064；3.西安西北民航项目管理公司，陕西 西安 710065)

沥青混合料的疲劳损伤与多种因素相关，如材料因素、控制方式、荷载大小、试验方法、加载波形等[1-2]。国内外学者从不同的角度研究了沥青混合料的疲劳损伤机理，针对不同的研究对象，提出了相应的疲劳损伤模型，使得沥青混合料的疲劳损伤的认识不断的深化[3- 6]。然而学者们关注的重点是沥青混合料的疲劳寿命与以上各因素之间的关系，很少去探究试件在疲劳试验过程中结构力学性能的变化。另外，现有沥青路面设计规范把路面结构层层底拉应力作为控制指标具有一定的局限性，其主要考虑了车轮荷载作用下路面结构底部的拉应力，忽视了路表疲劳对面层开裂的影响，导致了部分研究者认为路面疲劳是由结构层层底往上逐渐扩展。因此，笔者基于沥青混合料四点弯曲疲劳试验，建立了相应的力学模型，分析了不同的加载波形情况下小梁的刚度变化状况，模拟了路面结构层由上下两边往中间发展和由下往上扩展的情况。

1 沥青混合料疲劳试验加载波形

1.1 加载波形

车轮在路面上滚动是不断加载和卸载的过程，在计算过程中，一般将这种周期变化的形式用波来表示，在疲劳试验中小梁的荷载波形有3种形式，即正弦波、半正弦波和半正矢波[7]。对应的表达式和图形分别如式(1)和图1。

F(t)=Asinωt

F(t)=A·|sinωt|

(1)

式中：A为振幅；ω=2πf，f为频率。

图1 正弦波、半正弦波、半正矢波示意Fig.1 Schematic of sine wave, half sinewave and haversine wave

假设小梁截面下部受拉时所受的荷载为正，由图1可见，在正弦荷载作用的一个周期内，小梁经过加载-卸载-加载-卸载4个阶段，前半个周期内，小梁截面下部受拉，上部受压，而后半个周期内小梁截面的上部受拉，下部受压，并且两者是对称的。对于半正弦波和半正矢波，在一个周期内，小梁的荷载变化经过两个阶段，即加载-卸载，此时，小梁的下部始终处于受拉状态，而上部始终处于受压状态。

由以上分析可知，小梁的损伤与所选用的加载波形是密切相关的，当小梁为均质材料时，采用正弦波进行加载，小梁的疲劳损伤由梁的上下截面同时向中性轴位置扩展；当采用半正矢波或者半正弦波进行加载时，损伤会由梁的下部向上扩展。

1.2 不同加载波形对应的路面受力状态

疲劳试验中的加载波形需要与路面实际受力状态相对应，车轮荷载作用下路面受力状态如图2。由图2可见，当车轮行驶至B点时，路表A点、C点和车轮正下方的D点产生拉应力，车轮下方的路表B点为压应力；当车轮向C点方向行驶时，路表C点处由受拉状态变为受压状态，整个过程可以用正弦波来描述；在车轮荷载用下，当路表处产生的拉应力较小，即当图2中的A点和C点处的应力趋于0时，可以不考虑其影响，即认为路面从层底开始受重复拉应力作用而破坏，该过程可以假设为半正弦波和半正矢波。

图2 车轮荷载作用下路面受力状态Fig.2 Stress state of pavement under wheel load

2 沥青混合料刚度损伤模型

2.1 损伤模型的建立

为了模拟四点弯曲小梁疲劳试验，笔者设计一个简支梁模型，小梁的长度为L, 宽度为b, 高度为h，见图3，且假设小梁是均质的。

图3 应变疲劳小梁荷载Fig.3 Load on the small beam in strain fatigue test

由第1节的分析可知，小梁的损伤扩展有两种形式，在正弦波作用下，截面的损伤由两侧向中性轴位置扩展(图4)，在半正弦波和半正矢波作用下，截面的损伤由下部向上扩展(图5)。

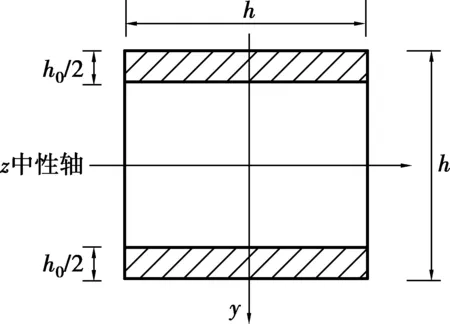
图4 损伤由截面上下两侧向中性轴位置扩展Fig.4 Damage developing from the upper and lower sides of the cross-section to the neutral axis

图5 损伤由截面下侧向上扩展Fig.5 Damage extending from lower sides of the section to the upper sides

其中z为中性轴位置，hn为截面中性轴到截面上表面的距离，h0为损伤区域的高度，当h0/h=0时，表示截面未损伤，当h0/h=1时，表示截面完全损伤。

2.2 疲劳试验终止条件

在应变疲劳试验中，一般认为小梁截面的终止劲度与初始劲度减小到一定的比值时即认为小梁截面破坏，劲度在循环荷载作用下衰变规律如图6。

图6 小梁劲度在循环荷载作用下的衰变规律Fig.6 Attenuation rule of small beam stiffness under cyclic loading

本研究中假设E0为终止劲度，E为初始劲度，考察E0/E为不同的比值时，损伤的扩展对截面刚度的影响。

2.3 小梁刚度

材料力学中，小梁的截面弯曲刚度以EI来表示，由弹性均质梁的挠曲线微分方程导出[8]：

EI=M/(1/ρ)=M/φ

(2)

式中：M为跨中最大弯矩；ρ为截面曲率半径；φ为截面曲率。

3 小梁相对刚度变化分析

3.1 损伤由上下两边往中间扩展时截面相对刚度变化分析

小梁的总高度为h，假设损伤由上下两侧向中间扩展时是对称的，则中性轴位置不变。

由图4及式(1)可得：

则截面损伤后的刚度为

相对刚度为

截面相对刚度随损伤扩展的变化规律如图7。

图7 损伤由上下两边向中间发展时截面相对刚度变化Fig.7 Variation of the relative stiffness of the cross-section when the damage develops from the upper and lower sides to the middle

3.2 损伤由截面下侧往上扩展时截面的相对刚度变化分析

当小梁截面的损伤由下侧往上扩展时(图5)，小梁截面的中性轴位置也会随之不断变化，由小梁截面合力为0的条件得：

整理后得小梁的中性轴位置：

为了便于分析，中性轴与截面上表面的距离采用hn/h来表示，中性轴位置随损伤扩展时的变化规律见图8。

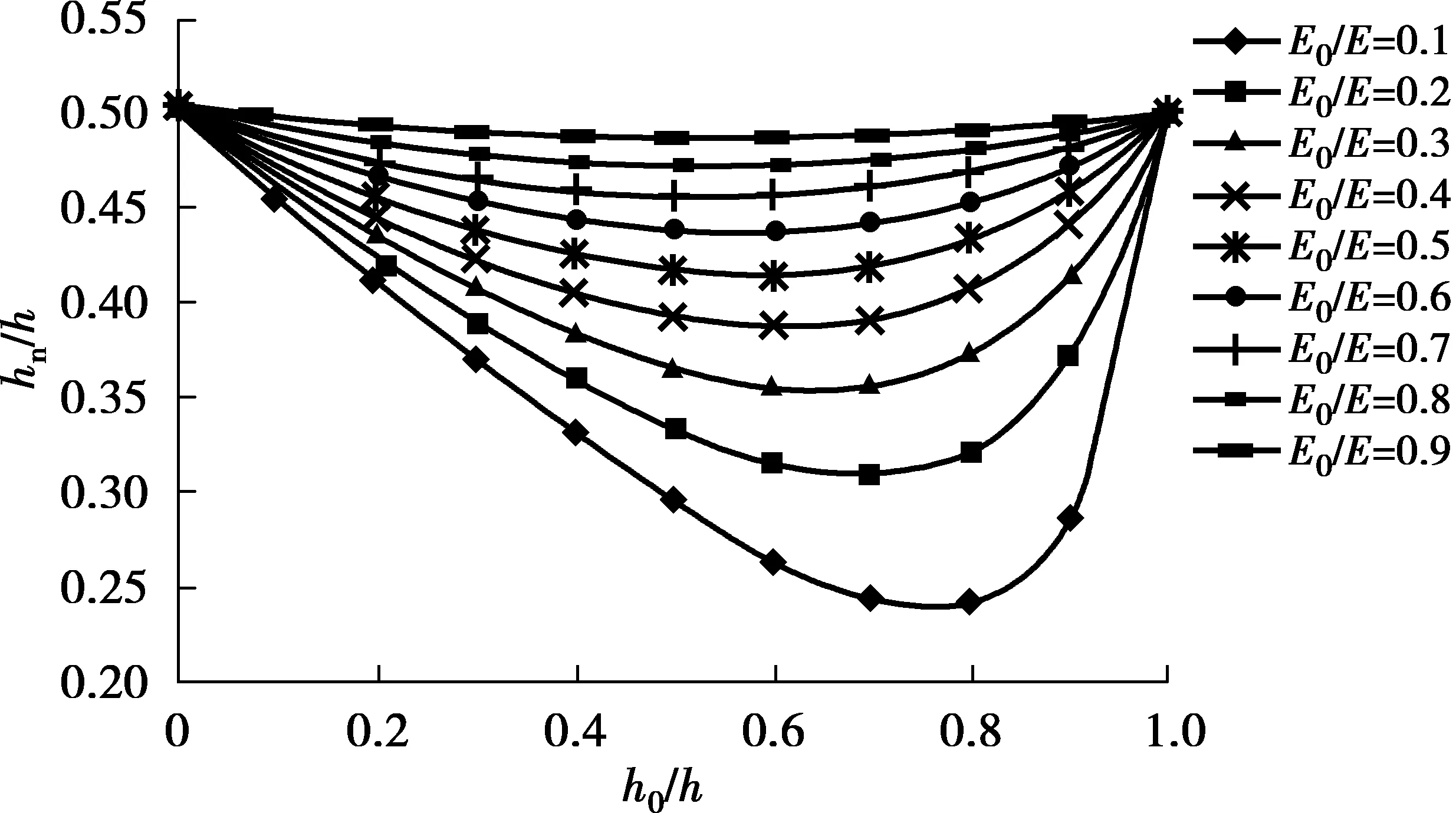
图8 损伤由小梁截面下侧往上发展时截面中性轴位置的变化Fig.8 Variation of the neutral axis position of the cross-section when damage develops from the lowers sides to the upper sides

由式(2)得：

则截面损伤后的刚度：

截面相对刚度随损伤扩展的变化规律如图9。

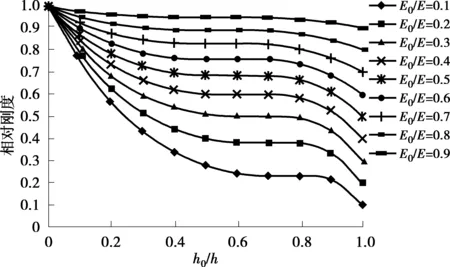
图9 损伤由小梁下表面往上发展时截面相对刚度变化Fig.9 Variation of the relative stiffness of the cross-section when the damage develops from the lower sides to the upper sides

由图8可见，当损伤由小梁的下表面向上逐渐扩展时，小梁中性轴与上表面的距离hn从初始的0.5h先减小然后再增大，最后中性轴又回到0.5h处，在整个变化过程中，hn存在一个极小值，当E0/E越小时，极小值越小，并且出现极值点的位置相对较晚。

由图9可见，小梁截面刚度的变化大致可以分为3个阶段：①小梁的刚度下降较大；②小梁的刚度变化较为平缓；③小梁的刚度下降幅度又有所变大，并且E0/E越大，第2阶段越明显。

4 损伤沿截面线性扩展时小梁截面的相对刚度变化分析

以上所讨论的损伤是完全的，即认为损伤区域内部各处的损伤都达到了小梁的终止劲度后才会继续发展。而实际小梁的损伤区域内部的损伤严重程度有可能是不同步的，即首先损伤的部位最先达到小梁的终止劲度，而后损伤部位的劲度会大些，在本节中假设损伤区域的劲度是线性变化的，分别如图10和图11。

图10 损伤由上下两边向中间发展Fig.10 Damage developing from the upper and lower sides of the section to the middle

图11 损伤由小梁截面下侧向上发展Fig.11 Damage developing from the lower sides to the upper sides of the cross-section of the small beam

4.1 损伤由两侧往中间扩展时截面相对刚度变化

由图10所示，损伤由上下两侧往中性轴扩展，模量在上下两边最小为E0，沿着损伤区域向内部逐渐增大，到h0/2处为E，在损伤区域，纵坐标y处的模量为

由式(2)得：

则刚度为

截面相对刚度随损伤扩展的变化规律如图12。

图12 损伤由上下向中间发展时截面相对刚度变化Fig.12 Variation of the relative stiffness of the cross-section when the damage develops from the upper and lower sides to the middle

4.2 损伤由截面下侧往上扩展时截面的相对刚度变化

由截面合力为0的条件得

整理后得小梁的中性轴位置：

中性轴位置随损伤扩展时的变化规律见图13。

图13 损伤由小梁下表面往上发展时截面中性轴位置的变化Fig.13 Variation of the neutral axis position of the cross-section when the damage develops from the lower sides to the upper sides of the small beam

由式(1)和式(2)得

则截面的刚度为

截面的相对刚度随损伤扩展的规律见图14。

图14 损伤由小梁下表面往上发展时截面相对刚度的变化Fig.14 Variation of the relative stiffness of the cross-section when the damage develops from the lower sides to the upper sides of the small beam

由图13可见，随着损伤的扩展，小梁中性轴与截面上表面的距离hn由0.5h先减小然后再增加；同3.2节，中性轴在变化过程中会出现一个极小值，E0/E越小，则极小值越小；并且当整个截面都损伤后，E0/E越小，中性轴距离截面上表面的距离越近。

由图14可见，截面的刚度会随着损伤的扩展而逐渐增大，E0/E越小，则刚度下降的幅度越大。

5 结 论

沥青混合料的损伤变化规律与加载采用的波形相关，在正弦波作用下，小梁的损伤由上下截面同时向中性轴位置发展，而在半正矢波或半正弦波荷载作用下，小梁的损伤由截面下侧向上扩展。基于欧拉公式理论，笔者建立了相应理论模型对以上两种情况进行探讨，得出了以下结论：

1)在正弦波作用下，小梁的相对刚度在初始阶段下降较快，而后期下降速度较慢。

2)在半正弦波或者半正矢波作用下，小梁的中性轴与截面上表面的距离hn由初始的0.5h逐渐减小，当达到一定的值时，又逐渐加大，最后又返回到0.5h处。

3)在半正弦波或者半正矢波作用下，小梁的相对刚度下降分为3个阶段，首先下降较快，随后进入稳定变化阶段，最后小梁的刚度又会有所下降。

4)分析了损伤沿截面线性扩展时截面的相对刚度变化，当损伤由两侧向中间扩展时，小梁的相对刚度在初期下降较快，随后变缓；当损伤由截面下侧往上扩展时，小梁的中性轴与截面上侧的距离hn由初始的0.5h先减小后增大，截面的相对刚度变化在初始阶段下降较大，随后逐渐变缓，最后下降幅度又会增加。

[1] 张肖宁，尹应梅，邹桂莲.不同空隙率沥青混合料的粘弹性能[J].中国公路学报，2010, 23(4): 1- 6.

ZHANG Xiaoning, YIN Yingmei, ZOU Guilian. Viscoelastic performance of asphalt mixture with different void contents[J].ChinaJournalofHighwayandTransport, 2010, 23(4): 1- 6.

[2] 许志鸿，李淑明，高英，等.沥青混合料疲劳性能研究[J].交通运输工程学报，2001,1(1): 20-24.

XU Zhihong, LI Shuming, GAO Ying, et al. Research on fatigue characteristic of asphalt mixture[J].JournalofTrafficandTransportationEngineering, 2001, 1(1): 20-24.

[3] 谢军，郭忠印.沥青混合料疲劳响应模型试验研究[J].公路交通科技，2007，24(5)：21-25.

XIE Jun, GUO Zhongyin. Research on fatigue model of asphalt mixtures[J].JournalofHighwayandTransportationResearchandDevelopment, 2007, 24(5): 21-25.

[4] 关宏兴，张起森，郑健龙. 沥青混合料粘弹性疲劳损伤模型研究[J].力学与实践，2007，29(2):50-53.

GUAN Hongxin, ZHANG Qisen, ZHENG Jianlong. Viscoelastic fatigue damage model of bituminous mixture[J].MechanicsinEngineering, 2007, 29(2): 50-53.

[5] 郑健龙，吕松涛. 沥青混合料非线性疲劳损伤模型[J]. 中国公路学报，2009,22(5)：21-28.

ZHENG Jianlong, LV Songtao. Nolinear fatigue damage model for asphalt mixtures[J].ChinaJournalofHighwayandTransport, 2009, 22(5): 21-28.

[6] 关宏兴. 沥青混合料粘弹性疲劳损伤性能研究[D].长沙：中南大学，2005.

GUAN Hongxin.AResearchonViscoelasticFatigueDamageModelofAsphaltMixture[D]. Changsha: Central South University, 2005.

[7] 王旭东. 沥青路面材料动力特性与动态参数[M]. 北京：人民交通出版社，2001.

WANG Xudong.DynamicCharacteristicsandDynamicParametersofAsphaltPavementMaterials[M]. Beijing: China Communications Press, 2001.

[8] 孙训方，方孝淑，关来泰. 材料力学[M]. 北京：高等教育出版社，2006

SUN Xunfang, FANG Xiaoshu, GUAN Laitai.MaterialsMechanics[M]. Beijing: Higher Education Press, 2006.