基于SWAN模型的南中国海“莫拉菲”台风浪研究
陈 橙,李 焱
(福州大学 土木工程学院,福建 福州 350116)
0 引言
我国的南中国海海域频繁受到台风的侵袭,台风产生的台风浪对海岸工程造成严重的破坏,并威胁到沿海地区居民的生命财产安全。据统计,每年仅由台风向岸浪对我国海岸防护工程的破坏、对近岸海域船舶和海水养殖业的危害,所造成的经济损失就超过7亿元[1]。因此,越来越多的学者开始对风浪场进行模拟[2-6]。海浪模式已发展至第三代,具有代表性的有WAM l21[7]、WAVEWATCH III(WW 3)和SWAN[8]。一般来说,WAM和WAVEWATCH被设计专门应用在整个海洋的尺度上,而SWAN有一些对浅水的额外数学化描述,它更适用于浅海海域。
目前对于台风莫拉菲的研究多为风场[9]以及降水[10],鲜有台风浪的模拟结果。本文以“0906”号台风“莫拉菲”为例,利用基于能量平衡方程的第三代近岸海浪数值模式SWAN[11]对南中国海台风浪进行数值模拟研究,并对台风浪的组成机制进行了探讨,以期对今后水运工程的建设以及台风浪的防灾减灾提供有益的参考。
1 数值模式介绍
1.1 风场模式
气压分布采用圆对称的Myers模型,其气压分布形式为:
(1)
式中:P0为台风中心气压;P∞为台风外围气压,取值1.013 3 kPa;r为计算点至台风中心的距离;r0为最大风速半径,具体表示为:
r0=28.52tanh[0.087 3(φ-28)]+
(2)
式中:φ是台风中心点的纬度,Vf是台风中心的移行风风速。
对(1)式求r的偏导得:
(3)
梯度风则可以表示为:
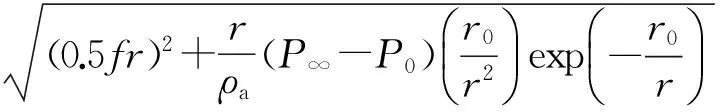
(4)
式中:ρa为空气密度,取值1.29 kg/m3;f为科氏力参数,f=2ωsin∅,ω是地球自转角速度,∅是计算点的纬度。
移行风场采用宫崎正卫公式,其形式为:
(5)
式中:r为计算点至台风中心的距离,Vx和Vy分别是台风中心移动速度的正东分量和正北分量。Vx和Vy可以通过经纬度变化进行差分化求得,表示为:
Vx=111 000(θt+Δt-θt)cosφt/Δt
(6)
Vy=111 000(φt+Δt-φt)/Δt
(7)
式中:θt和φt分别为t时刻台风中心的经度和纬度,θt+Δt和φt+Δt分别为t+Δt时刻台风中心的经度和纬度,Δt为两计算时刻的时间间隔。
台风风场模型的表达式可由(6)、(7)式的移行风表达式与(4)式的梯度风表达式相迭加:
(8)
式中:c1和c2是修正系数,α是计算点和台风中心的连线与正东方向的夹角,β是梯度风与海面风的夹角。
1.2 海浪模式
SWAN以二维动谱密度表示随机波,动谱密度N(σ,θ)与能谱密度E(σ,θ)之间关系为N(σ,θ)=E(σ,θ)/σ。
在笛卡尔坐标系下,动谱平衡方程可表示为:
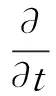
(9)
上式方程左边第一项为随时间的变化率;第二和第三项表示动谱密度在地理坐标空间x、y方向上的传播;第四项表示由于流场和水深所引起的动谱密度在相对频率σ空间的变化;第五项表示动谱密度在谱分布方向θ空间的传播,亦即水深及流场而引起的折射;方程右边的S代表以谱密度表示的源汇项,包括风能输入、白浪、破碎、海底摩擦、波-波非线性相互作用等物理过程。
在球坐标系下,动谱平衡方程可表示为:
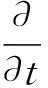
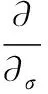
(10)
式中:λ为经度,φ为纬度。
2 数值模式介绍
2.1 台风选取
“0906”号台风“莫拉菲”的台风中心路径如图1所示。其生成时间为2009年7月15日,生成地为西北太平洋菲律宾以东海域。生成后一路向西北方向行进,于7月19日上午2时登陆于深圳市盐田区,登陆时的中心风力逼近40 m/s。此次台风造成了近2亿元的直接经济损失。根据建国以来的台风资料统计,“0906”号台风“莫拉菲”的生成时间、生成地点、中心风力、登陆地、登陆强度等在南中国海的台风中具有十分典型的代表性,因此被选取为研究对象。研究区域为10°N~30°N,105°E~125°E。在研究区域中,选取台风路径左侧点A(114°E,18°N)、台风路径上的点B(116°E,21°N)、以及台风路径右侧点C(117°E,22°N)三个点,以探究台风浪的组成机制。
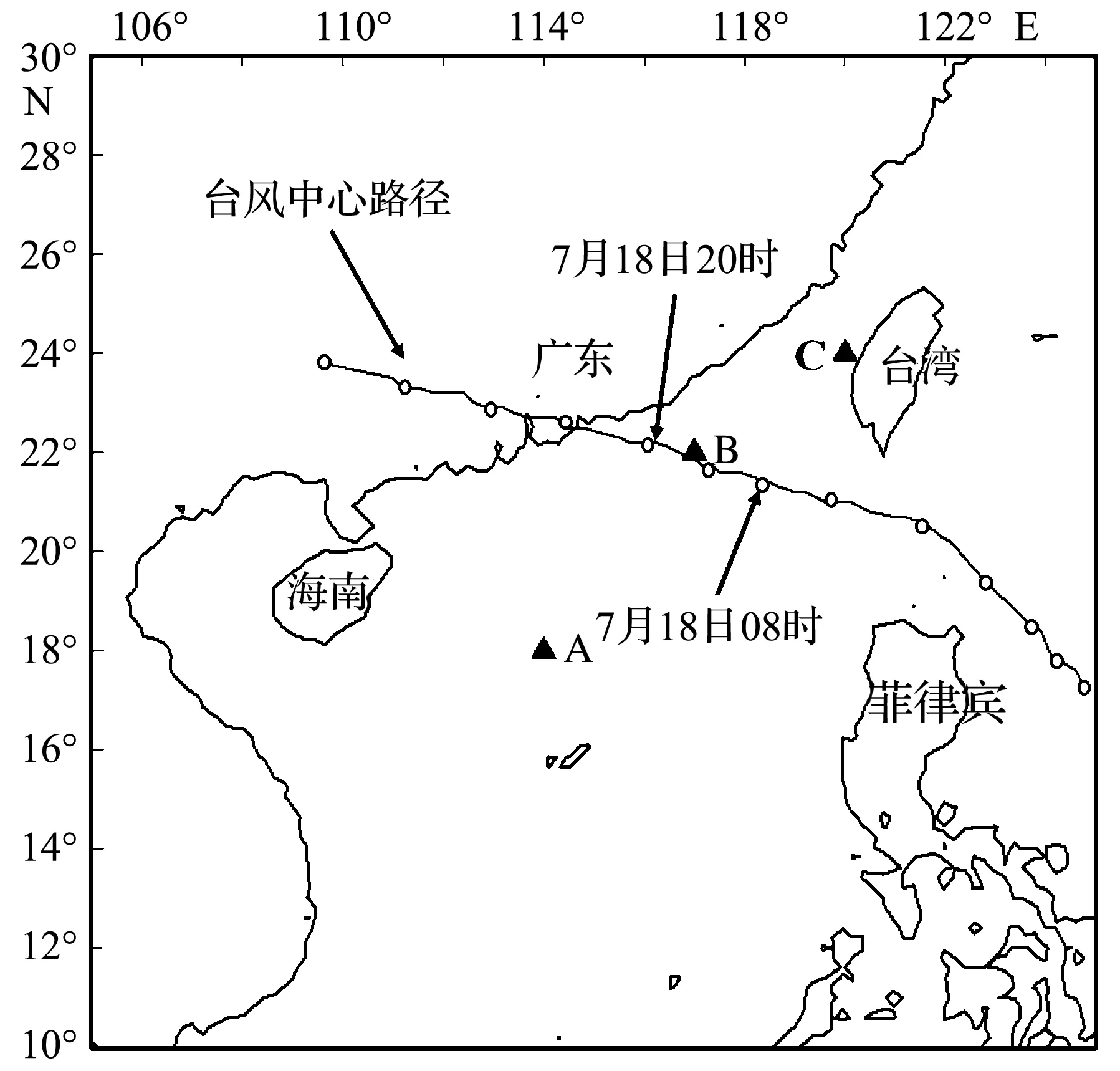
图1 “0906”号台风“莫拉菲”的中心移动路径以及试验点位置Fig.1 Moving track of No.0906 typhoon Molave and test positions
2.2 模型参数
计算区域、水深输入区域、风场的输入区域均相同,为(10°N~30°N,105°E~125°E)。模型采用了球坐标系下的非静态模式,时间和空间上的离散方法为S&L格式,谱空间的离散为中心差分格式。对于计算区域,模型的空间分辨率为4′×4′,时间步长为10 min,从2009年7月16日20时积分至2009年7月19日14时共66 h。风能的输入采用风场模型的计算结果,风能输入区域的空间分辨率为18.18′×18.18′,时间步长为6 h,从2009年7月16日20时积分至2009年7月19日14时共66 h。水深输入的空间分辨率为4′×4′。在频率和方向的二维谱空间分辨率上,频率的计算从0.01~0.5,以指数分布划分为25个;方向的分段为60个,分辨率为6°。风能的输入考虑了线性增长和指数增长两部分,其中线性增长采用CAVALERI和MALANOTTE-RIZZOLI[12]的表达式,指数增长采用KOMEN et al[13]的研究成果。海底摩擦造成的能量损耗采用Collins公式,其它参数的设置均取模型默认值。模型的开边界无波浪输入。
3 结果与讨论
3.1 台风风场模拟
风场的模拟结果可直接影响到波浪场的模拟。图2a和2b分别为 2009年7月18日08时与2009年7月18日20时的风场图,其中箭头长度表示风速大小,箭头方向表示该点的风向。由模拟结果可知,在台风气压梯度的影响下,台风中心附近的风场大致呈现出圆对称分布,各计算点的风向都大致指向沿台风中心逆时针的方向,符合北半球热带气旋规律。这是由于气旋中心气压低,气团由四周流向中心,而在北半球地转偏向力使物体运动方向偏右,即风向在气压梯度力的右侧,由此,风从四周吹向中心形成了逆时针方向的转动。特别地,台风中心处风场的分布比较复杂,且最大风速处于台风中心附近(接近30 m/s),风速大小沿着台风中心向外围递减,台风的影响一般仅限于几百公里范围内,外围风速较小。
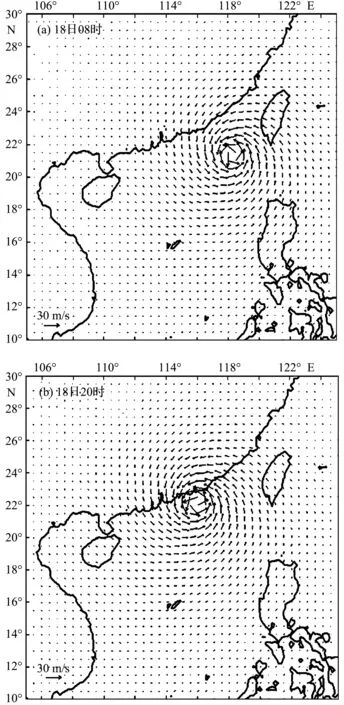
图2 数学模型计算出的台风场图Fig.2 Results of typhoon wind field from numerical model
3.2 台风引发的波浪场模拟
基于风场的数模结果,模拟出了波浪场,图3a和3b分别为 2009年7月18日08时与2009年7月18日20时的波浪场图,其中箭头长度表示有效波高,箭头方向表示该点的台风浪方向。由模拟结果可知,波浪场在一定程度上遵循台风场的分布规律,即台风中心附近波高大,台风外围波高小,且呈现逆时针旋转分布。然而波浪场并非完全与风场一样呈现圆对称分布,而是呈现出椭圆分布,这是由于波浪场还受到地形的影响。其原因在于,海浪场由风场驱动,但又受到耗散过程和波-波相互作用的影响。由于地形的变化以及海底高程改变,浅水作用增强,波浪消耗能量加大,因此垂直于岸线的波高比其周围平行于岸线的波高略小,故呈现椭圆分布。
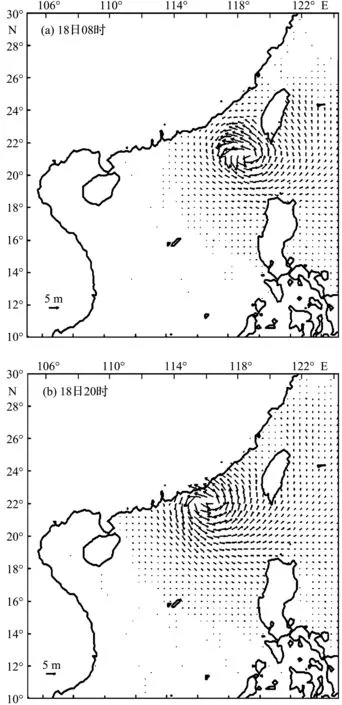
图3 数学模型计算出的波浪场图Fig.3 Results of wave field from numerical model
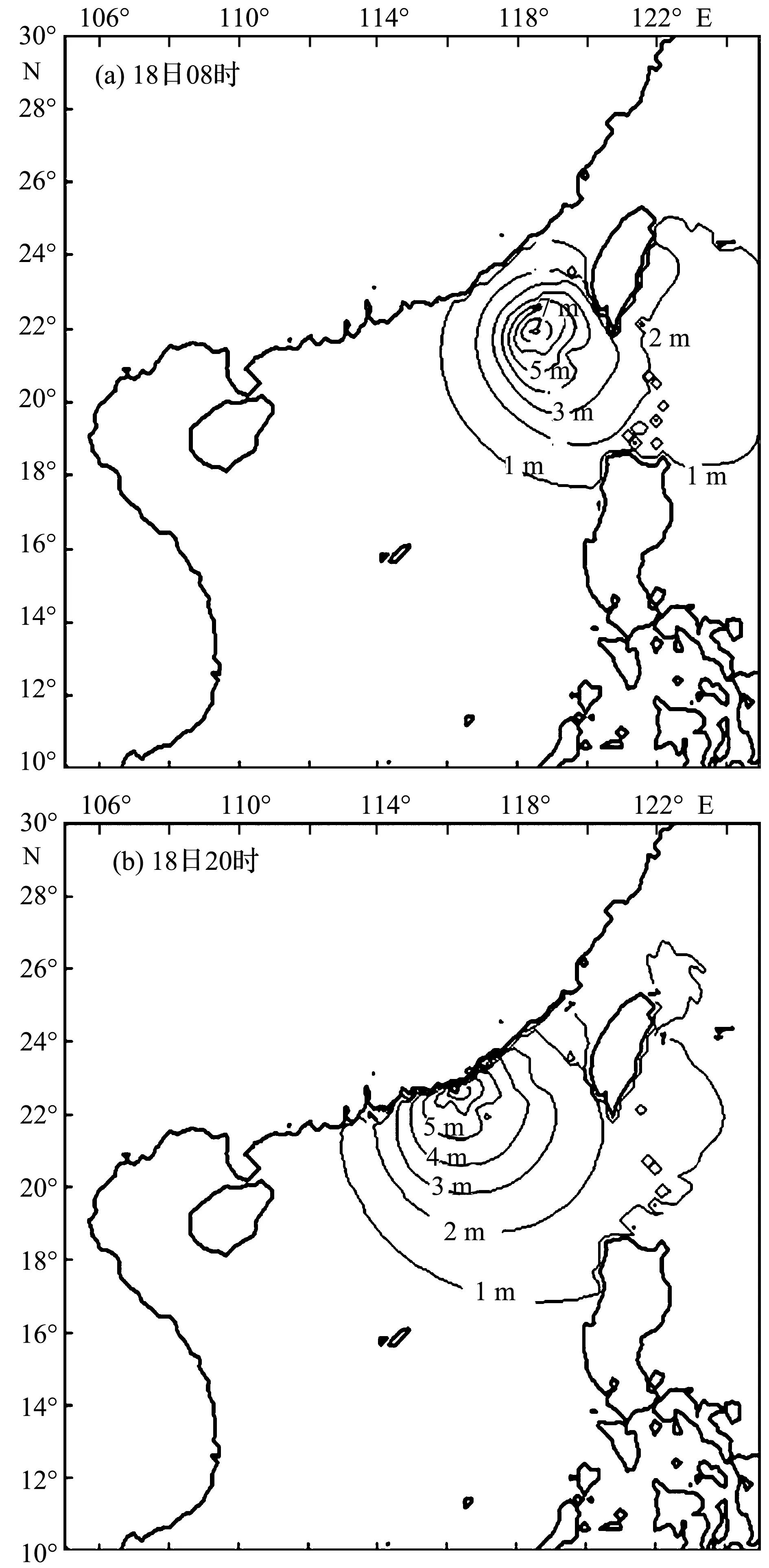
图4 数学模型计算出的有效波高等值线图Fig.4 Results of significant wave height contour from numerical model
3.3 有效波高等值线模拟结果
根据波浪场的模拟结果,亦可绘制出有效波高等值线图,图4a和4b即分别为 2009年7月18日08时与2009年7月18日20时相对应的有效波高等值线图。由图可知,有效波高等值线的分布并非完全遵循风场的圆对称分布形式,而是有较大程度的扭曲。这是由于有效波高等值线的分布不仅受到台风风场的影响,还受到岸线以及海底地形的影响,该结果与波浪场的分布结果相类似。此外,有效波高等值线亦遵循中心高外围低的规律,即在台风中心附近的有效波高可达到7 m,而在台风外围波高等值线则逐渐降到1 m以下。最大风速圈通常对应着最高波高圈。本模型中,5 m波高圈范围在15 m/s风圈强度范围内。而在浅水区域,波高圈范围小于风圈范围,这是因为靠近陆地,浅水作用对海浪的影响增强,海浪场的能量耗散增加。
3.4 台风浪组成机制讨论
在台风发生的整个历时中,随着台风的接近与远离,南中国海各特定点的风速和波高历时曲线均呈现先增大后减小的规律。为了探究整个台风浪演化特征,本文选取A、B、C三个点(见图1)以模拟风速、波高随时间的变化,进而讨论台风浪的组成机制。
图5a为A点处(距台风中心较远,位于台风中心路径左侧,周围无岛屿)的风速和波高历时曲线图。如图所示,该点风速随时间先增大后减小,而波高随时间缓慢增加,再缓慢减小,且波高的峰值明显滞后于风速的峰值。这是由于该点离台风较远,受到风力影响较小,形成波浪的主要因素为涌浪,即由台风中心路径处的波浪以涌浪的形式传播至A点。
图5b为B点处(位于台风中心路径上)的风速和波高历时曲线图。如图所示,该点风速和波高的变化同步且趋势一致,均呈现先增后减,且在同一时刻达到峰值。这是由于该点距离台风中心近,形成波浪的主要因素为台风。
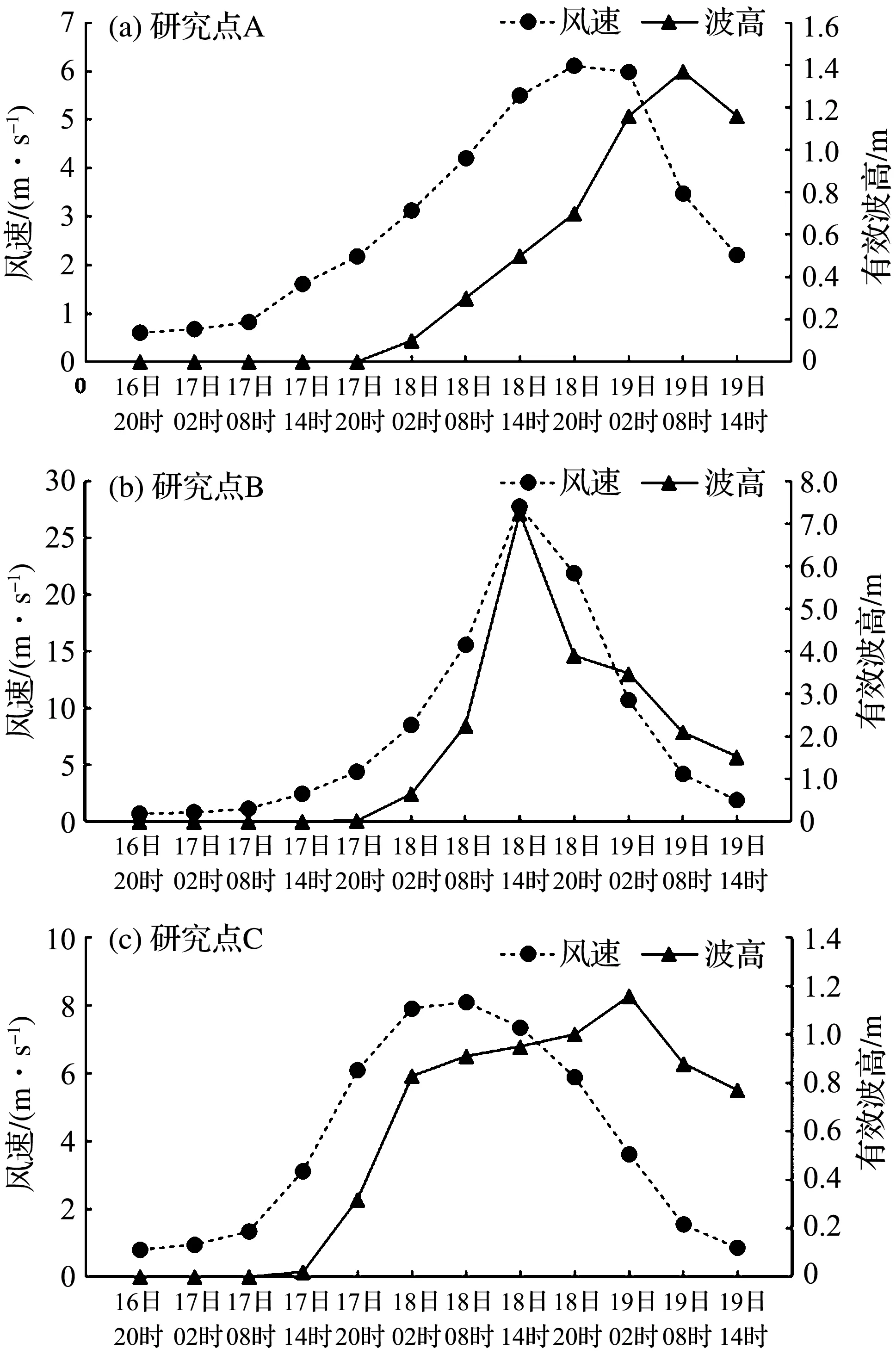
图5 研究点的风速、波高历时曲线图Fig.5 Time histories graph of wind speed and wave height for three test positions
图5c为C点处(距台风中心较远,位于台风中心路径右侧,周围有台湾岛)的风速和波高历时曲线图。如图所示,该点风速随时间先增大后减小,而波高随时间缓慢增加,再缓慢减小,且波高的峰值比A点更加滞后于风速的峰值,波高也比A点处的稍小。这是由于C点附近的台湾岛阻碍了来自东南方的涌浪,因而削弱了波高、滞后了峰值。由此可见,岸线与地形(例如岛屿效应)也会对台风浪具有一定的影响。
4 小结
本文以“0906”号台风“莫拉菲”为例,基于第三代海浪模式SWAN建立了适用于南中国海的台风浪数值模型。模拟结果显示台风风场呈圆对称分布,风向都大致指向沿台风中心逆时针的方向,风速大小沿着台风中心向外围递减。台风引发的波浪场与风场相似,有效波高呈现为中心高外围低,波向呈现逆时针旋转,且呈椭圆对称分布。有效波高等值线亦为中心高外围低,且等值线形状受地形与岸线的影响较大。最后通过探讨台风浪组成机制可知,台风浪由风浪和涌浪二者组成,还受海底地形与岸线(例如岛屿效应)的影响。
致谢河海大学港口海岸与近海工程学院赵红军副教授为本文提供了帮助,谨致谢忱!。
[1]YANGChun-cheng,DAIMing-rui,GAOZhi-hua,etal.Anumericalpredictionmethodfortyphoonwaves[J].ActaOceanologicaSinica,1996,18(1):1-12.
杨春成,戴明瑞,高志华,等.一种台风浪的数值预报方法[J].海洋学报,1996,18(1):1-12.
[2]CHENXi,MINJin-zhong,SHAWen-yu,etal.Asimulatonofnearshoretyphoonwaves[J].MarineScienceBulletin,2003,22(2):9-16.
陈希,闵锦忠,沙文钰,等.近岸海浪模式在中国东海台风浪模拟中的应用——数值模拟及物理过程研究[J].海洋通报,2003,22(2):9-16.
[3]ZHAOHong-jun,SONGZhi-yao,XUFu-min,etal.NumericalsimulationoftyphoonwavesintheSouthChinaSea——acasestudyoftyphoonChanchu[J].TheOceanEngineering,2010,28(3):128-134.
赵红军,宋志尧,徐福敏,等.南中国海台风浪数值模拟研究——以台风"珍珠"为例[J].海洋工程,2010,28(3):128-134.
[4]WANGHong-chuan.Applicationofcombineddistributionbetweenwaveheightandset-upinducedbystormsurge[J].Port&WaterwayEngineering,2014(3):51-56.
王红川.风暴潮增水和台风浪联合分布在北仑港中的应用[J].水运工程,2014(3):51-56.
[5]QIQing-hui,ZHUZhi-xia,DONGPei-hua,etal.NumericalsimulationonDamreytyphoonstormsurgeinLianyungangseaarea[J].Port&WaterwayEngineering,2016(5):19-23.
齐庆辉,朱志夏,东培华,等.连云港海域“达维”台风风暴潮数值模拟[J].水运工程,2016(5):19-23.
[6]TANGYan-ping,LINXiang.NumericalsimulationandcharacteristicanalysisoftyphoonwavesinFujiancoastal[J].Port&WaterwayEngineering,2017(4):53-59,93.
唐艳平,林祥.福建沿海台风浪数值模拟及特性分析[J].水运工程,2017(4):53-59,93.
[7]WAMDIG.TheWAMmodel—Athirdgenerationoceanwavepredictionmodel[J].JPhysOceanogr,1988,18:1 775-1 810.
[8]BOOIJN,RISRC,HOLTHUIJSENLH.Athird-generationwavemodelforcoastalregions,Part1:Modeldescriptionandvalidation[J].JGeoRes,1999,104(4):7 649-7 666.
[9]LILei,LIUYan-xiang,ZHANGLi-jie,etal.Numericalstudyofthefine-scalewindstructureoverthepaiyamountaininShenzhenduringthelandingperiodoftyphoonMolave[J].JournalofTropicalMeteorology,2012,28(6):911-918.
李磊,柳艳香,张立杰,等.台风“莫拉菲”登陆期间深圳排牙山周边风场结构的数值模拟研究[J].热带气象学报,2012,28(6):911-918.
[10]LIANGHong-sheng.DiagnosticanalysisontrackandprecipitationoftyphoonMolave[J].AdvancesinMarineScience,2011,29(1):28-36.
梁宏升.台风“莫拉菲”移动路径和降水诊断分析[J].海洋科学进展,2011,29(1):28-36.
[11]XUFu-min,ZHANGChang-kuan,TAOJian-feng.MechanismandapplicationofathirdgenerationwavemodelSWANforshallowwater[J].AdvancesinWaterScience,2004,15(4):538-542.
徐福敏,张长宽,陶建峰.浅水波浪数值模型SWAN的原理及应用综述[J].水科学进展,2004,15(4):538-542.
[12]CAVALERIL,MALANOTTE-RIZZOLIP.Windwavepredictioninshallowwater:Theoryandapplications[J].JGeophysRes,1981,86(C11):10 961-10 973.
[13]KOMENGJ,HASSELMANNS,HASSELMANNK.Ontheexistenceofafullydevelopedwind-seaspectrum[J].JPhysOceanogr,1984,14:1 271-1 285.

