基于最优尺度的生产建设扰动图斑识别
亢庆,姜德文,扶卿华,王晓刚
监测在城市建设、矿山、水利工程等生产建设活动中,因挖损、占压、堆弃等行为引起的地表扰动作用,对水土保持具有重要的意义。随着对地观测技术的进步,利用空间分辨率<5 m的高分辨率影像对扰动地块(影像上称为扰动图斑)识别和提取是遥感影像分类研究重要内容,也是《全国水土保持信息化规划(2013—2020年)》和《全国水土保持信息化实施方案(2014—2016年)》提出的“天地一体化”生产建设项目监管思路的核心。
目前,针对生产建设扰动图斑的遥感提取及识别的研究较少,可以借鉴的研究主要体现在对矿产资源开发现状调查与监测以及土地利用/覆盖动态监测等方面,包括人机交互方法提取矿产开采点、状态等信息[1],以及基于差值法、主成分分析法、变化矢量分析法[2]检测土地利用/覆盖的变化位置和范围等,这些方法以检测地物光谱特征为唯一切入点,在以TM/ETM+为代表的中低分辨率影像上,得到极大的发展;但是随着影像空间分辨率的跃升,高分辨率影像可清晰表达的地物边界、几何形状等空间特征不能被上述方法利用,容易出现“同物异谱”“同谱异物”现象,以及因高分辨率影像丰富的光谱信息而产生“椒盐效应”,于是有了面向对象的分类方法的发展[3]。该类方法以具有相同光谱、几何形状、纹理等特征[4]的像元集合为分类对象,理论上可以避免基于光谱特性分类方法存在的“椒盐效应”等问题,成为现阶段研究的重要方向。
面向对象的分类包括影像分割和影像分类2个步骤。影像分割是将影像切割成若干个对象,并要求对象内的像元具有相同的地物特征(包括光谱、几何形状和纹理等特征),是整个分类过程的基础和关键,决定了影像分类(对分割对象的识别)的精度[5-6]。在影像分割研究中,获取合适的分割尺度,也[6]称为最优分割尺度,即分割对象满足对象内的光谱、几何形状和纹理等地物特征的同质性和相邻对象间的地物特征的差异性均达到最大,并且拟提取和识别的地物可以通过1个或者多个对象表达出来的条件时的分割尺度。需要说明的是,这里的尺度问题虽然仍旧属于空间问题,但是有别于传统基于像元的分类中出现的空间分辨率问题,主要是因为面向对象的分类研究的对象不再是像元,而是具有光谱、几何形状和纹理相似性的对象),是现阶段关注的焦点,尤其是在基于多尺度分割技术的eCognition软件出现之后。传统的最优尺度获取方法以分类者的多次尝试和主观判断为依据,效率低下且存在主观不确定性[7-8]。除“试错”法之外,还有参与方法和非参与方法[9]2类:前者根据与已知地物的吻合程度来判断最优尺度,需要输入人工预先勾画出的边界,如矢量距离指数法[10]、面积比均值法[11];后者不需要人工的参与,主要分析对象内部的同质性与对象间的异质性,建立尺度与二者之间的函数曲线,依据对象内同质性最大、对象间异质性最大的原则[8],或者依据内部同质性的变化率随尺度的变化规律,客观地选取一个合适的尺度,代表性的方法有分割评价指数[12]、局部方差方法[3]、目标函数法[8]。从实际生产应用的角度而言,非参与方法更具有普适性[9],其中,又以局部方差方法和目标函数法理论较为扎实,应用也更为广泛。
综合研究进展,笔者以生产建设扰动图斑的高分辨率遥感识别为研究目标,首先对比和分析了局部方差法和目标函数法获取生产建设扰动图斑最优分割尺度的可行性,然后采用面向对象的监督分类对生产建设扰动图斑进行了识别和提取,并依据现场调查和无人机航片对识别结果进行评估。
1 研究方法
1.1 面向对象的影像分割
影像分割方法大体上可以分为基于阈值、基于边界和基于区域3类,其中:基于阈值的方法依赖于阈值的选择,在复杂的遥感影像,效果较差;基于边缘的分割方法往往难以得到闭合且连通的边界,且容易产生边界错分的现象;而基于区域的方法具有原理简单、无须预知类别数目等优点,得到广泛的应用,尤其是分形网络演化算法(Fractal Net Evolution Approach,FNEA)[13],即 eCognition 中多尺度分割技术中应用到的方法[14]。FNEA是一种区域生长的算法,基本思路是以1个像元为种子,依据光谱、形状等多特征加权值,不断合并周围与种子像元有相同或者相似性质的像元,直至满足停止生长条件。
FNEA算法的理论基础可表示为
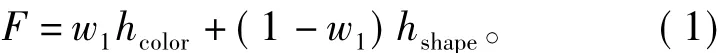
式中:F为尺度参数,是判断一个对象是否继续生长的关键,F过小会造成分割后的对象破碎、时耗过长,属于“过分”现象,F过大,则会造成对象内混合了多种地物类型的像元,属于“欠分”或“混分”现象;hcolor为光谱因子,由各波段的光谱值乘以相应的权重累加得到;w1为光谱因子的权重,取值为0~1;hshape为形状因子:
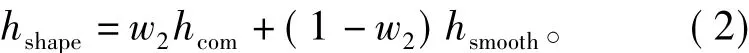
式中:hcom为紧致度因子,用于优化分割对象的紧凑程度,取值介于0~1;hsmooth为光滑度因子,用于优化分割对象边界的光滑程度,抑制边缘的过度破碎,取值介于0~1;w2为紧致度的权重。
1.2 最优分割尺度
最优分割尺度是指分割后的对象能够清楚地刻画出地物的边界,目标地物可以通过1个或者多个分割对象表达出来,分割后的图像既不能“过分”,也不能“欠分”或“混分”。那么,获取最优分割尺度的原则是在保证不“欠分”或“混分”的基础上,适合目标地物的最大尺度。
1.2.1 局部方差方法 L.DRGU爩等[3]基于对象的局部方差随尺度F变化规律提出了一个最优分割尺度获取方法。其基本思路:随着分割尺度的增加,对象内属于同种地物的像元增加,影像的局部方差也随之缓慢增加,当增加到一定程度之后,对象内会混入其他地物类型的像元,此时对象内光谱值的方差会迅速增大,对象间的光谱异质性降低,局部方差的变化率发生转折。那么,局部方差变化率的转折处就是不同地物类型的最优分割尺度。影像的局部方差为
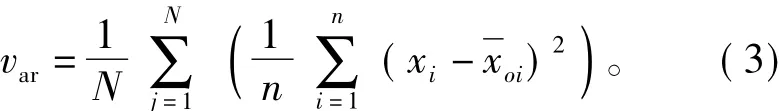
式中:N为图像中对象的个数;n为对象中像元的个数;x为对象的光谱值;xo为对象的灰度值均值。
局部方差变化速率
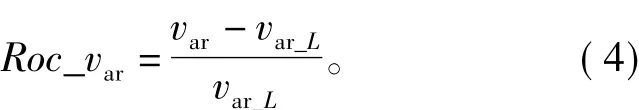
式中var_L为比var小一个尺度间隔的局部方差。
1.2.2 目标函数方法 影像分割的理想结果是分割后的对象具有良好的内部同质性,同时相邻对象之间具有良好的异质性;但两者的最大值并不一定能在同一尺度上取得,那么最优分割尺度可能是基于二者的平衡。G.Espindola等[8]的思路首先是分别计算对象内像元光谱值的同质性和异质性,并分别进行归一化处理,之后建立目标函数,目标函数取最大值时的尺度F为最优分割尺度。
1)对象内同质性。
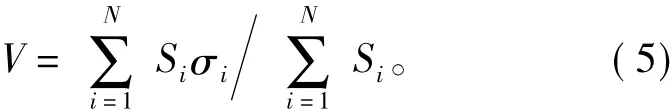
式中:V为表征对象内同质性参量;Si和σi分别为第i个对象的面积和光谱值标准差。
2)对象间的异质性。
使用Moran's I指数来衡量分割对象之间的异质性[15]:
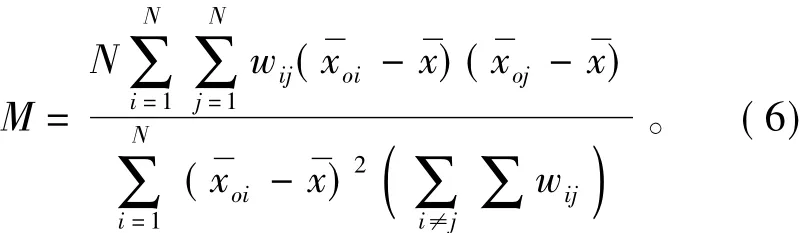
式中:M为Morna's I指数;wij为空间关系权重,如果对象i和对象j相接,wij=1,否则 wij=0;为整幅影像的光谱平均值。
3)目标函数F(x)。
依据V和M在不同尺度下的最大最小值,分别将二者归一化处理,得到Vnorm和Mnorm目标函数
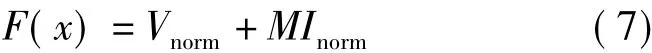
式中:Vnorm为归一化处理后的对象内同质性 V;Mnorm为归一化处理后的Moran's I指数。
1.3 扰动图斑的识别
计算出最优分割尺度之后,还需要对分割后的影像进行识别。识别算法采用eCognition中的面向对象的监督分类法,该方法能够对光谱、几何形状、纹理等特征描述及计算。整个识别工作包括:首先,依据现场调研、无人机航片以及前期获取的其他统计资料,为生产建设扰动图斑建立解译标志,并依据解译标志的光谱特征和几何特征为监督分类建立训练样本;其次,用最邻近法对生产建设扰动图斑识别;最后,利用现场调研和无人机航片对分类结果进行校验,如果识别精度满足要求,则直接导出生产建设扰动图斑,否则,则挑选出混分、漏分的像元,并建立相应的数据库,之后再次回归监督分类步骤,直至识别精度达标。
综合上述思路,本研究的基本流程见图1。
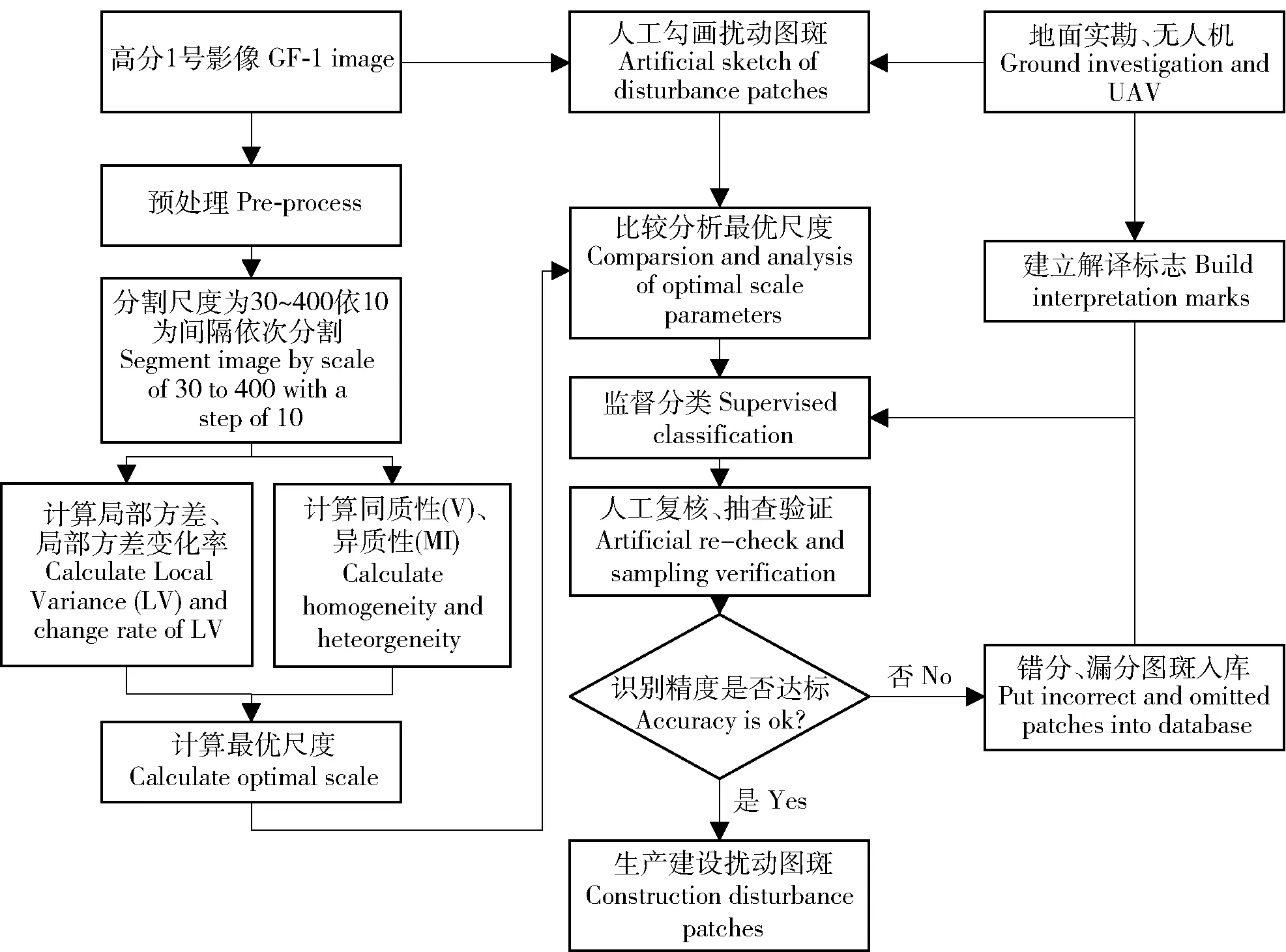
图1 生产建设扰动图斑识别流程图Fig.1 Procedure for automatically identifying construction disturbance patches
2 研究区及解译标志的建立
2.1 研究区域及数据预处理
选用2016年广东省生产建设项目水土保持监管示范县内一块典型样区(图2),结合高分1号(GF-1)影像展开研究。如图2所示,研究区内地物类型复杂且破碎,包括零星分散的小型居民点(图中呈不规则分布的灰色部分)、大片的林草地、夹在居民点和林草地之间的小块农田、道路、水塘、生产建设扰动地块(包括未完成的建筑,以及取土、堆放建筑渣料等造成的裸露地块),区内图像尺寸为2 249像元×2 465像元。

图2 研究区GF-1标准假彩色合成影像Fig.2 Standard false color composite of GF-1 image of the study area
2.2 解译标志的建立与分析
根据地面实地调查及无人机航拍所掌握的背景知识,针对生产建设项目的建设时期,建立用于识别生产建设扰动图斑的解译标志,解译标志的建立参考现场调查照片、影像以及光谱特征、光谱频率和形状特征等影像特征(表1)。
由表1可以看出,生产建设扰动图斑内的光谱亮度范围较大,并且随着生产建设的进展逐步扩大,3个不同时期的值依次为946、1 089.2和1 486.5。与光谱亮度范围呈同样变化规律的还有扰动图斑的亮度标准差,分别为136.0、145.9和211,相反,扰动图斑的光谱亮度均值则随着生产建设的进展逐渐减小。
3 结果及讨论
3.1 影像分割
影像分割在eCognition环境下进行,分割尺度F的变化范围为30~400,步长为10,FNEA分割方法涉及到的其他因子(光谱因子、形状因子、波段比重)在多次的分割过程中均保持一致,即光谱因子和紧致度因子分别设为0.6和0.5,波段权重为1∶1∶1∶1。

表1 生产建设项目解译标志Tab.1 Interpretation mark of construction project
3.2 获取最优分割尺度
当分割尺度F为310时(图3a),生产建设扰动图斑像元混入了一些小型居民地和绿色植被,属于分割尺度F过大造成的“欠分”或“混分”现象,没能对生产建设项目进行有效分割,不利于提高后续信息的识别和提取。当分割尺度F为300时(图3b),分割对象内的像元较为纯净,其边界能较清晰地刻画出生产建设扰动图斑的边界;因此,尺度300是最适宜分割尺度。其作为真值用于检验目标函数法和局部方差方法获取的最优分割尺度该尺度作为生产建设扰动图斑的最优分割尺度真值,可用于验证目标函数方法和局部方差方法计算的最优分割尺度。

图3 不同尺度F的分割效果(a:F为310;b:F为300)Fig.3 Segmentation results of different segmentation scales(a:310;b:300)
如图4所示,研究区内的对象个数在30~140的尺度范围内由48 140个迅速减少到3 130个,之后缓慢减少,而对象的平均面积则是随着尺度F的增加而呈近似线性增加,二者线性相关的确定系数R2=0.95。
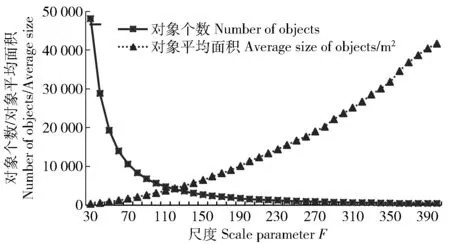
图4 分割尺度与对象个数、平均面积的关系Fig.4 Relationship between segmentation scales and number of objects/average size of objects
随着对象个数的减少和对象平均面积的增加,对象内包含的像元个数增加,光谱亮度变化范围增加,导致对象的局部方差增大(图5)。依据局部方差方法的思路,合适的分割尺度通常发生在局部方差的变化率式(4))由增加到减小的转折处,符合条件的分割尺度有240、270、310,由图2和表1所示的生产建设扰动图斑解译标志可以发现,扰动图斑内光谱亮度值变化较大,且形状多属于不规则,在此背景条件下,适合扰动图斑的分割尺度则相对较大,可推断出310是基于局部方差方法得到的最优分割尺度,略微大于真值。
随着F的增加,对象的个数减少,对象内部的同质性V(式(5))增加,归一化后的 Vnorm减小(图6)。对象间的异质性M数则随尺度增大而呈下降趋势,与 G.Espindola等[8]和殷瑞娟等[16]的研究结果相似,而归一化后的异质性Mnorm呈增加的趋势(图6)。平衡了对象内同质性和对象间异质性的目标函数F(x)随F的变化规律整体上呈下降趋势,线性斜率为-0.007;但是在F为300时刻取得最大值1.2,依据目标函数确定最优分割尺度的原理,尺度300为最优分割尺度,与真值一致。
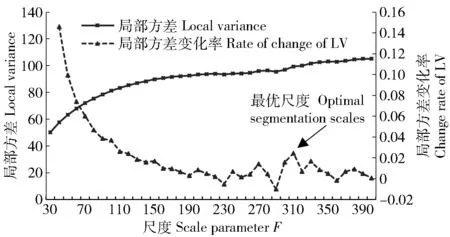
图5 对象局部方差和方差变化率随尺度F的变化规律Fig.5 Changes in local variance and change rate of LV with segmentation scale increasing
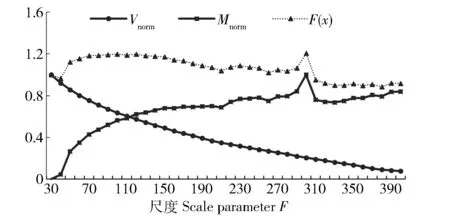
图6 V norm、M norm和目标函数F(x)随尺度F的变化规律Fig.6 Changes in V norm,M norm and object function F(x)with segmentation scale increasing
3.3 生产建设扰动图斑的识别
基于最优分割尺度得到的分割影像,利用野外调查、无人机航片得到解译标志(表1),为面向对象的监督分类建立训练样本,样本的选择综合考虑了光谱、纹理及形状等特性信息。利用面向对象的监督分类中的最邻近方法实现对生产建设扰动图斑的识别(图7中红色部分)。同时,为了更好地说明最优分割尺度与识别精度的一致性,计算了其他分割尺度下的生产建设扰动图斑,但考虑到分割尺度低于150时,区域内图斑个数超过3 000,图像分割过于破碎,使得地物类型弱化、甚至丢失了纹理和形状特征,不利于面向对象分类实施,必然会造成识别精度的降低,因此本文只对≥150分割尺度生产建设扰动图斑进行了识别。
依据现场调查的图片、空间分辨率低于0.1 m的无人机航片和其它前期获取的统计资料,人工绘制了研究区域内生产建设扰动范围(图7蓝色方框标注范围),并以此为真值,对计算机识别的生产建设扰动图斑进行了精度检验,精度检验采用用户精度(用户精度=Sr/Sa×100,式中:Sr为被正确识别出的面积;Sa为真实面积(图7蓝色方框内的面积))和制图精度(制图精度=Sr/Si×100,式中Si为被计算机识别出的面积)。
精度检验结果见表2,生产建设扰动图斑的制图精度和用户精度均是在最优分割尺度下取得极大值,分别为86.3%和84.2%,说明最优分割尺度与识别精度存在一致性。对比最优分割尺度与其他较小分割尺度,可以发现影像分割尺度并非越小越好,当分割尺度很小时,虽然对象内部光谱无差异,但是同类地物不同对象之间的光谱差异就会明显的表现出来,同时对象的形状几何信息也会在一定程度上丢失,会造成地物识别的精度明显偏低。

图7 最优分割尺度下的生产建设扰动图斑识别结果Fig.7 Identified result of construction disturbance patches based on optimal segmentation scale

表2 各分割尺度下的生产建设扰动图斑识别精度Tab.2 Accuracies of construction disturbance patches on different segmental scales%
最优分割尺度下用户精度略小于制图精度,即被计算机识别出的生产建设扰动图斑面积大于实际面积,说明识别结果中出现了其他类型地物被错分为生产建设扰动图斑,与图7所示的最优分割尺度下的生产建设扰动图斑识别结果较为一致,且这些错分部分多出现在道路以及小型居民点的周围,主要原因是施工中的生产建设项目与其相毗邻的道路或者小型居民点的光谱差异较小,同时地表复杂且不规则的格局加大了识别难度。此外,在生产建设项目内部,一些轻度扰动的地块,因为与自然地物光谱特征差异较小,容易漏分。对于生产建设扰动图斑识别中出现的错分/漏分图斑,建立了错分/漏分数据库,为研究区域及以外的其它地区提高分类精度提供参考依据。
4 结论
1)基于目标函数方法获取的最优分割尺度与实际结果一致,而基于局部方差方法计算得到的最优分割尺度略微偏大,偏大3.3%。
2)最优分割尺度与识别精度存在一致性。基于面向对象的监督分类方法,在最优分割尺度下的生产建设扰动图斑识别精度较其他分割尺度较高,制图精度和用户精度分别达到86.3%和84.2%。
笔者结合目标函数方法和局部方差方法计算了生产建设扰动图斑最优分割尺度。值得指出的是,本文计算出的最优分割尺度在不同的遥感影像源、不同地表覆盖特征下可能会存在差异,但是获取生产建设扰动图斑最优分割尺度的过程和思路具有普适性。今后会针对不同特征的地表覆盖对生产建设扰动图斑的最优分割尺度做进一步的研究。
[1] 张焜,马世斌,刘丽萍.基于SPOT5数据的盐湖矿产开发及矿山环境遥感监测[J].国土资源遥感,2012,24(3):146.ZHANG Kun,MA Shibin,LIU Liping.Remotesensing monitoring of the mineral resources exploration and mining environment of the Salt Lake based on SPOT5 Data[J].Remote Sensing For Land & Resources,2012,24(3):146.
[2] 王丽云,李艳,汪禹芹.基于对象变化矢量分析的土地利用变化检测方法研究[J].地球信息科学学报,2014,16(2):307.WANG Liyun,LI Yan,WANG Yuqin.Research onland use change detection based on an object-oriented change vector analysis method[J].Journal of Geo-information Science,2014,16(2):307.
[3] DRGU爩L,TIEDE D,LEVICK SR.ESP:a tool to estimate scale parameter for multiresolution image segmentation of remotely sensed data[J].International Journal of Geographical Information Science,2010,24(6):859.
[4] RYHERD S,WOODCOCK C.Combining spectral and texture data in the segmentation of remotely sensed images[J].Photogrammetric Engineering and Remote Sensing,1996,62(2):181.
[5] GAO Y,MAS J F,KERLE N,et al.Optimal region growing segmentation and its effect on classification accuracy[J].International Journal of Remote Sensing,2011,32(13):3747.
[6] KIM M,WARNER T A,MADDEN M,et al.Multi-scale GEOBIA with very high spatial resolution digital aerial imagery:scale,texture and image objects[J].International Journal of Remote Sensing,2011,32(10):2825.
[7] WHITESIDE T G,BOGGSG S,MAIER SW.Comparing object-based and pixel-based classifications for mapping savannas[J].International Journal of Applied Earth Observation and Geoinformation,2011,13(6):884.
[8] ESPINDOLA G,CMARA G,REISI,et al.Parameter selection for region-growing image segmentation algorithms using spatial autocorrelation[J].International Journal of Remote Sensing,2006,27(14):3035.
[9] ZHANG H,FRITTS J E,GOLDMAN S A.Image segmentation evaluation:a survey of unsupervised methods[J].Computer Vision and Image Understanding,2008,110(2):260.
[10] 于欢,张树清,孔博,等.面向对象遥感影像分类的最优分割尺度选择研究[J].中国图象图形学报,2010(2):352.YU Huan,ZHANG Shuqing,KONG Bo,et al.Optimal segmentation scale selection for object-oriented remote sensing image classification[J].Journal of Image and Graphics,2010(2):352.
[11] 汪求来.面向对象遥感影像分类方法及其应用研究[D].南京:南京林业大学,2008.WANG Qiulai.Study on object-oriented remote sensing image classification and its application-taking urban vegetation extraction in Futian Shenzhen city as example[D].Nanjing:Nanjing Forestry University,2008.
[12] 陈春雷,武刚.面向对象的遥感影像最优分割尺度评价[J].遥感技术与应用,2011,26(1):96.CHEN Chunlei,WU Gang.Evaluation of optimal segmentation scale with object-oriented method in remote sensing[J].Remote Sensing Technology and Application,2011,26(1):96.
[13] BAATZ M,SCHPE A.Object-oriented and multiscale image analysis in semantic networks[C].Proceedings of the 2nd international symposium:operationalization of remote sensing,1999.August 16th–20th,Enschede.ITC,Enschede,The Netherlands.7 -13.
[14] DURO D C,FRANKLIN SE,DUBM G.A comparison of pixel-based and object-based image analysis with selected machine learning algorithms for the classification of agricultural landscapes using SPOT-5 HRG imagery [J].Remote Sensing of Environment,2012,118:259.
[15] JOHNSON B,XIE Z.Unsupervised image segmentation evaluation and refinement using a multi-scale approach[J].ISPRS Journal of Photogrammetry and Remote Sensing,2011,66(4):473.
[16] 殷瑞娟,施润和,李镜尧.一种高分辨率遥感影像的最优分割尺度自动选取方法[J].地球信息科学学报,2013,15(6):902.YIN Ruijuan,SHI Runhe,LI Jingyao.Automatic selection of optimal segmentation scale of high-resolution remote sensing images[J].Journal of Geo-information Science,2013,15(6):902.

