一种基于攻防估分算法的智能五子棋游戏设计

潘雨馨，李文彬

（1.岳阳市一中，岳阳414006；2.湖南理工学院，岳阳414006）

0 引言

五子棋是一种两人对弈的纯策略型棋类游戏，是世界智力运动会竞技项目之一，是一种增强思维、趣味横生、大众喜爱的智力游戏。五子棋对弈双方分别使用黑白两色的棋子，下在棋盘直线与横线的交叉点上，先形成5子连线者获胜[1]。

设计和研发智能型五子棋游戏程序，可以在休闲时为人们提供对战的乐趣，可以帮助新手在一定程度上提高棋艺。目前，关于五子棋游戏的智能算法主要有：估分函数[2-3]、博弈树搜索[4-5]、深度学习[6]等。其中，博弈树是基于未来可能的所有或部分棋局进行搜索而做出有利的判断，由于博弈树的规模庞大，需要设计复杂的算法进行状态空间剪枝。深度学习则是通过与海量棋局中进行强化学习，从而使程序具备不断改进的自我学习能力，但学习过程需要先进的高性能计算设备的支持。而估分函数主要是基于当前棋局的有利形势判断进行落子决策，计算量较小，易于实现，非常适合大众型智力游戏设计。

现有基于估分函数的五子棋算法，主要通过棋型判断计算攻防得分，并根据攻防得分的大小确定进攻或防守的落子位置。这类算法往往在攻防策略选择上比较单一，很容易被对手适应。本文提出基于多种攻防策略的估分选择算法，考虑在棋型分值较高时，选择最有利进攻或防守位置的落子；在整体棋型分值较低时，选择在攻防差距最大的位置落子，使棋局朝最有利于AI方发展。

1 数据结构设计

AI版五子棋游戏的主要数据结构包括五个矩阵：棋盘状态矩阵currBoard、进攻得分矩阵offScore、防守得分矩阵defScore、连子空位矩阵conBlank、棋型矩阵chessSituation。其中：

（1）棋盘状态矩阵currBoard是一个15×15的二维矩阵，每个元素的值表示棋盘上每个下棋点的状态：1表示黑棋，-1表示白棋，0表示没有棋子。

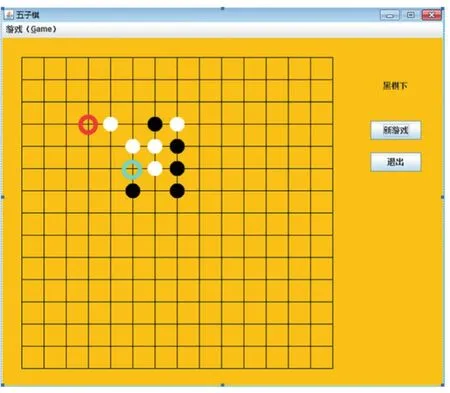
图1 五子棋游戏棋盘结构

（2）进攻得分矩阵offScore是一个15×15的二维矩阵，记录AI方的进攻得分，每个元素的值表示AI方在该位置放置棋子的得分。若该位置已有棋子，则置为0。

（3）防守得分矩阵offScore是一个15×15的二维矩阵，记录AI方的防守得分，每个元素的值表示棋手方在该位置放置棋子的得分。若该位置已有棋子，则置为0。

（4）连子空位矩阵conBlank是一个4×3的二维矩阵，记录从当前空位沿横、竖、撇、捺四个方向的连子和空位情况。例如，假设AI方是白棋，位置（4,4）的棋型说明如表1所示（红色圆圈标记），在行（横）方向，它的左空位数是3，连子数是2，右空位数是1。

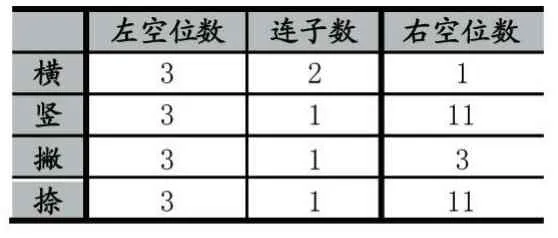
表1 位置(4,4)的连子和空位情况

（5）棋型矩阵chessSituation是一个2×5的二维矩阵，记录某位置成5、活4、死4、活3等棋型情况。五子棋的得分棋型大致可以分为以下几种：

成5：五子连珠。

活4：两边均不被拦截的四子连珠。

死4：一边被拦截的四子连珠。

活3：两边均不被拦截的三字连珠。

死3：一边被拦截的三字连珠，且另一边空位数不小于2。

活2：两边均不被拦截的二子连珠，且两边空位总数不小于3。

死2：一边被拦截的二子连珠，且另一边空位数不小于3。

活1：两边均不被拦截的单子，且两边空位总数不小于4。

死1：一边被拦截的单子，且另一边空位数不小于4。

例如，假设AI方是白棋，位置（6,6）的进攻得分棋型如表2所示（蓝色圆圈标记），横方向是死2，竖方向是死2，撇方向是活3，捺方向是活1。棋型矩阵chess-Situation矩阵的总和等于4。

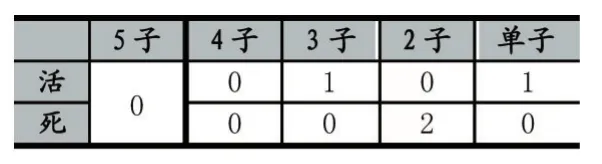
表2 位置(6,6)的得分棋型情况

2 核心算法设计

AI版五子棋游戏的核心算法包括：胜负判断算法、棋型估分算法和攻防选择算法。

2.1 胜负判断算法

在不考虑禁手的情况下，五子棋胜负判断算法主要通过横、竖、撇、捺四个方向是否存在五子连珠的情况。胜负判断算法判断每一次落子是否会导致棋局的输赢。胜负判断算法主要由两个子算法组成：获取落子位置连珠范围算法getRange()和五子连珠算法cont-Five()。其中getRange()取落子位置横、竖、撇、捺四个方向的棋子状态情况（用一维数组表示）；contFive()判断是否存在五子连珠。

算法1落子位置连珠范围算法getRange()public boolean getRange(int row,int col){

//行

if(contFive(currBoard[row]))

return true;

//列

int b[]=new int[15];

for(int k=0,i=0;i

b[k]=currBoard[i][col];

if(contFive(b))

return true;

//主对角线

int c[]=new int[15];

for(int k=0,i=Math.max(0,row-col),j=Math.max(0,col-row);i

c[k]=currBoard[i][j];

if(contFive(c))

return true;

//副对角线

int d[]=new int[15];

for(int k=0,i=Math.min(14,row+col),j=Math.max(0,col+row-14);i>=0&&j

d[k]=currBoard[i][j];

if(contFive(d))

return true;

return false;

}

算法2五子连珠算法contFive()public boolean contFive(int[]a){

for(int i=0;i<=a.length-5;i++){

int s=0;

for(int k=0;k<5;k++)

s=s+a[i+k];//连续5个之和

if(s==5||s==-5)

return true;

}

return false;

}

2.2 棋型估分算法

棋型估分算法计算空子位置的攻、防得分，给AI程序提供落子参考。棋型估分算法主要由三个子算法组成：连子空位计算calc_conBlank()、棋型评估算法calc_situation()、攻防计分算法scoring()。其中，calc_conBlank()计算落子位置的连子情况及两端的空位情况；calc_situation()计算沿横、竖、撇、捺四个方向出现的成5、活4、死4等各种棋型的统计情况；scoring()根据落子位置的棋型统计情况计算该位置的进攻、防守得分。

算法3连子空位算法calc_conBlank()

public void calc_conBlank(int f){//f表示棋子类型

if(currBoard[i][j]==0){//行

int k=1;//左

temp[0][0]=1;//temp表示连子空位矩阵con-Blank

while(j-k>=0&&currBoard[i][j-k]==f){//连子

temp[0][0]++;

k++;

}

while(j-k>=0&&(currBoard[i][j-k]==0||currBoard[i][j-k]==f)){//左空位或同色棋子

temp[0][1]++;

k++;

}

k=1;

while(j+k<15&&currBoard[i][j+k]==f){

temp[0][0]++;

k++;

}

while(j+k<15&&(currBoard[i][j+k]==0

||currBoard[i][j+k]==f)){

temp[0][2]++;

k++;

}

}

}

算法4棋型评估算法calc_situation()public void calc_situation(int[][]temp){

for(int h=0;h<4;h++){

if(temp[h][0]>=5)

s[4][0]++;

else if(temp[h][0]==4&&(temp[h][1]>=1&&temp[h][2]>=1))

s[3][1]++;//活4

else if(temp[h][0]==4&&(temp[h][1]>=1||temp[h][2]>=1))

s[3][0]++;//死4

else if(temp[h][0]==3&&(temp[h][1]>=1&&temp[h][2]>=1))

s[2][1]++;//活3

else if(temp[h][0]==3&&(temp[h][1]+temp[h][2]>=2))

s[2][0]++;//死3

else if(temp[h][0]==2&&(temp[h][1]+temp[h][2]>=3&&

temp[h][1]>=1&&temp[h][2]>=1))

s[1][1]++;//活2

else if(temp[h][0]==2&&temp[h][1]+temp[h][2]>=3)

s[1][0]++;//死2

else if(temp[h][0]==1&&(temp[h][1]>=3&&temp[h][2]>=3))

s[0][1]++;//两端空位均超过3的单子

else if(temp[h][0]==1&&temp[h][1]+temp[h][2]>=4)

s[0][0]++;//单子}}

算法5攻防计分算法scoring()public void scoring(int f){

if(s[4][0]>=1)//成5

b=100;

else if(s[3][1]>=1||s[3][0]>=2||s[2][0]>=2||(s[3][0]>=1&&s[2][1]>=1))

b=90;

else if(s[2][1]==1&&s[2][0]>=1)//活 3死 3

b=80;

else if(s[3][0]==1)//死4

b=70;

else if(s[2][1]==1)//活3

b=60;

else if(s[1][1]>=2)//双活2

b=50;

else if(s[2][0]==1)//死3

b=40;

else if(s[1][1]==1)

b=30;

else if(s[1][0]>=1)

b=20;

else if(s[0][1]>=1)

b=15;

else if(s[0][0]>=1)

b=5;

//将得分保存到进攻、防守矩阵

if(f==-1)

offScore[i][j]=b;

else

defScore[i][j]=b;

}

2.3 攻防选择算法

攻防选择算法off_def_choice()提供了4种策略进行攻防选择：在最大进攻得分位置落子、在最大防守得分位置落子、在最大攻防得分正差位置落子、在最大攻防得分负差位置落子。当最大攻防得分大于等于80时，根据最大攻防得分的大小，选择在最大进攻或防守位置落子。当最大攻防得分小于80时，根据最大攻防正负差得分的大小，选择在最大正差或最大负差位置落子。

算法6攻防选择算法off_def_choice()public void off_def_choice(){

int max1=0;//最大进攻得分

int max2=0;//最大防守得分

int max3=0;//最大进攻防守得分正差

int max4=0;//最大进攻防守得分负差

//进攻防守得分

max1=scoring(-1);

max2=scoring(1);

//进攻防守差距计分

int[][]gap=new int[15][15];

for(int i=0;i<15;i++)

for(int j=0;j<15;j++){

gap[i][j]=offScore[i][j]-defScore[i][j];

if(gap[i][j]>max3)max3=gap[i][j];

if(gap[i][j]

max4=gap[i][j];

}

//进攻防守选择

if(max2>=80||max1>=80){

if(max2>=max1)

System.out.println("在最大防守得分位置落子");

else

System.out.println("在最大进攻得分位置落子");

}else if(Math.abs(max3)>Math.abs(max4))

System.out.println("在最大攻防得分正差位置落子");

else

System.out.println("在最大攻防得分负差位置落子");

}}

3 结语

本文针对五子棋游戏，设计了一种基于攻防得分的智能评估算法。对每个可落子的位置，计算该位置连子数和两端空位数，统计该位置出现成5、活4等各种棋型的情况，进一步计算该位置进攻和防守得分，并设计攻防选择四种策略，指导AI程序完成落子。与其他基于单一攻防策略的算法相比，该算法具有更好的棋局判断能力。

[1]刘瑞.五子棋人工智能算法设计与实现[D].华南理工大学,2012.

[2]徐建.五子棋的一种价值的估算[J].智能计算机与应用,2016,6(5):90-92.

[3]卓明敏,黄正亮,廖小于.五子棋级数算法[J].福建电脑,2012,28(4):94-96.

[4]张明亮,吴俊,李凡长.五子棋机器博弈系统评估函数的设计[J].计算机应用,2012,32(7):1969-1972.

[5]王长飞,蔡强,李海生.智能五子棋算法的设计实现[J].系统仿真学报,2009,21(4):1051-1054.

[6]史忠植.突破通过机器进行学习的极限[J].科学通报,2016(33):3548-3556.