循环荷载下非饱和黏弹性地基一维固结特性分析
秦爱芳,吕康立
传统的土力学研究基本上都是以饱和土为主,而在实际工程中,大多数的土处于非饱和状态,在干旱、半干旱地区尤为如此.对于工程中的非饱和土路堤和土坝等问题,若仍然用饱和土的理论来指导施工的话,将会影响工程建造的质量以及施工的进度.
对于非饱和土,典型的固结理论分别由Blight[1],Scott[2],Barden[3]和Fredlund等[4-5]提出,其中Fredlund固结理论比较完善且具有权威性.
对于饱和黏弹性地基固结问题,王奎华等[6]、蔡袁强等[7-8]、谢康和等[9]分别采用Merchant和Kelvin模型进行了大量的深入研究.对于非饱和黏弹性土地基在变荷载作用下的固结问题,国内外相关研究还较少.Shan等[10]对恒载和加荷随时间指数变化时多层非饱和土弹性地基的固结进行了研究.Zhou等[11]研究了多种初始条件和边界条件下,变荷载作用时的非饱和土弹性地基一维固结问题.Liem等[12]将非饱和土弹性地基的固结理论拓展到了二维空间.
对于非饱和黏弹性土地基一维固结问题,秦爱芳等[13-15]依据Fredlund非饱和土一维固结理论,并对其进行了一些假设,得到了瞬时加荷下黏弹性土地基一维固结的半解析解.本工作在上述研究的基础上,对实际工程中常用的3种循环荷载(正弦荷载、三角形荷载和梯形荷载)作用下的黏弹性地基,采用Merchant黏弹性模型求得了一维固结的半解析解,并对其固结特性进行了分析.研究结果对工程中的实际问题具有指导作用.
1 半解析解的推导
1.1 计算模型和本构方程
本工作中的基本假定与Fredlund的非饱和土一维固结理论[5]相同,计算模型如图1所示.非饱和土层的顶面为透水透气面,底面为不透水不透气面.土层厚度为H,施加的循环荷载为σ(t),坐标原点设在地表,深度方向(z轴)以竖直向下为正.取底面积为1、高度为dz的单元体V0=1×1×dz为研究对象.
黏弹性模型采用Merchant模型(三单元模型),该模型由一个Kelvin体(由一个弹性体和一个黏性体并联而成)和一个弹性体串联组成,如图2所示.Merchant模型的本构方程为

式中,σ为应力,η为黏性体的黏滞系数,ε为应变,E0和E1为弹性体的弹性模量.对式(1)作关于时间t的Laplace变换,得到

式中,s为Laplace变量.

图1 计算模型Fig.1 Calculation model
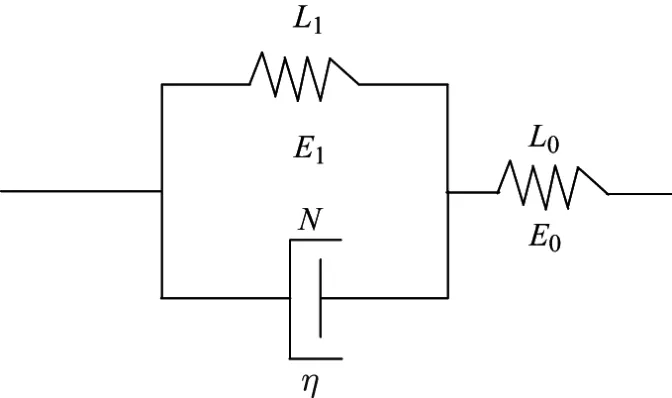
图 2 Merchant模型Fig.2 Merchant model
1.2 任意加荷时Laplace变换下的解
本工作依据Fredlund一维固结理论的本构方程[5],针对Merchant黏弹性地基模型,采用李氏比拟法,引入Laplace变换下的柔度系数V(s)代替线弹性模型中的常数1/E,再通过线弹性情况下的液相和气相的控制方程、Darcy定律及Fick定律,采用文献[13]中的方法,得到Laplace变换下的4个微分方程.

式中:

其中
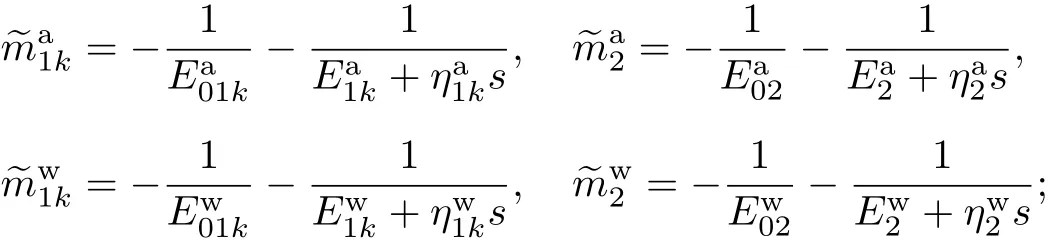
将式(3),(4),(5),(6)写为矩阵形式的偏微分方程[13],即

式中,~X(z,s)=[~ua(z,s),~uw(z,s),~Ja(z,s),~vw(z,s)]T,

根据Cayley-Hamilton理论[16],式(7)的解的一般形式为

式中,T(z,s)=exp[zA(s)],S(z,s)=0T(z − ς)B(s)dς.由式(8)可得,土层顶面的状态向量与任意深度处状态向量的传递关系为

式中,T11∼T44及S1∼S4的含义同文献[13].
1.3 边界条件和初始条件
因为土层上表面为透气透水面,底面为不透气不透水面,所以边界条件为

初始条件为

将边界条件和初始条件代入式(9),可解得Laplace变换下任意深度处的超孔隙气压力~ua(z,s)、超孔隙水压力~uw(z,s)和土层压缩量~w(z,s),方法同文献[13].
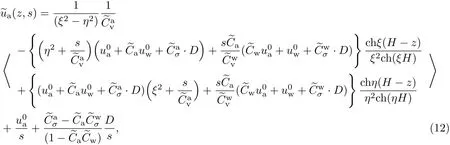

2 循环荷载及其Laplace变换下的解
2.1 正弦荷载

式中:σ0为外荷载的峰值,取σ0=100 kPa;w为圆频率,取w=10−6rad/s;t为荷载加载时间.

图3 正弦荷载Fig.3 Sinusoidal load
对式(15)作关于t的Laplace变换,可得

2.2 三角形荷载
三角形荷载如图4所示,表达式为


图4 三角形荷载Fig.4 Triangle load
对式(17)作关于时间t的Laplace变换,可得

式中,σ0=100 kPa,T=106s.
2.3 梯形荷载
梯形荷载如图5所示,表达式为

对式(19)作关于时间t的Laplace变换,可得

式中,σ0=100 kPa,T=106s.
将上述3种循环荷载情况下的~σ(s),σ(0)分别代入式(12),(13)和(14),可得Laplace变换下的解,然后再进行Laplace逆变换,即可求得3种循环荷载作用下任意深度的超孔隙气压力、超孔隙水压力及土层沉降量.
由于本工作中的~ua(z,s),~uw(z,s)和~w(z,s)非常复杂,通过Laplace逆变换无法直接获得超孔隙气压力、超孔隙水压力及土层沉降的数学表达式,因而需要通过数值法求解逆变换.本工作运用较常用且精度较高的Durbin和Crump方法[17],通过编制程序对~ua(z,s),~uw(z,s)和 ~w(z,s)进行Laplace逆变换.
3 算例分析
下面分析3种循环荷载作用下非饱和黏弹性地基固结过程中的超孔隙水压力、超孔隙气压力以及固结度随时间的变化规律.固结度为各时刻的土体沉降与土体最终沉降的比值,即Us=~w(z,t)/~w(z,∞).当加荷到一定时间,土体固结趋于稳定,在循环荷载作用下所能达到的最大沉降趋近于一固定值,即认为此最大沉降为土体固结的最终沉降~w(z,∞).
3.1 正弦荷载
图6为ka/kw=100时正弦荷载作用下超孔隙气压力、超孔隙水压力和固结度随时间的变化规律.由图可以看出,超孔隙气压力、超孔隙水压力的消散和土体的固结均随荷载呈周期性变化.超孔隙气压力在第一个周期内就消散到趋近于0,然后在0附近上下振动;超孔隙水压力在第一个周期内消散到0.2,然后在0.2附近上下振动,形成一段“平台期”,最后又消散到0,并在0附近上下振动;固结度在第一个周期前半段一直增大,随后上下振动(整体呈现逐渐固结趋势),最后在Us=1附近上下振动.

图6正弦荷载作用下非饱和黏弹性地基的固结特性随时间的变化(ka/kw=100)Fig.6 Change in consolidation characteristics of viscoelastic unsaturated soils for sinusoidal loading(ka/kw=100)
图7 为正弦荷载作用下ka/kw不同时超孔隙气压力、超孔隙水压力及固结度随时间的变化规律.由图可以看出,ka/kw的大小对超孔隙气压力的消散影响非常明显.当ka/kw较大时,超孔隙气压力在第一个周期就消散到趋近于0,之后在0附近上下振动;ka/kw越大,超孔隙水压力达到的峰值越小,超孔隙水压力消散越快;当ka/kw较小时,超孔隙气压力和超孔隙水压力的消散曲线的切线斜率几乎相同;ka/kw越大,固结度在周期内达到的峰值越大,固结速度越快.


图7 正弦荷载作用下ka/kw不同时非饱和黏弹性地基的固结特性随时间的变化Fig.7 Change in consolidation characteristics of viscoelastic unsaturated soils for sinusoidal loading at diあerent values of ka/kw
3.2 三角形荷载

图8三角形荷载作用下ka/kw不同时非饱和黏弹性地基的固结特性随时间的变化Fig.8 Change in consolidation characteristics of viscoelastic unsaturated soils for triangle loading at diあerent values of ka/kw
图8 为三角形荷载作用下ka/kw不同时超孔隙气压力、超孔隙水压力及土层沉降随时间的变化.由图可以看出,三角形荷载作用下超孔隙气压力、超孔隙水压力和固结度的变化规律与正弦荷载作用下的规律基本相同.ka/kw较大时,超孔隙气压力很快消散到0,然后在0附近上下振荡;ka/kw越大,超孔隙气、水压力消散越快,超孔隙气、水压力的峰值越小.超孔隙水压力虽不类似超孔隙气压力很快消散至0附近,但整体呈消散趋势(中心线向下倾斜).另外,由图8(c)可以看出,ka/kw越大,固结速度越快.
3.3 梯形荷载
图9为梯形荷载作用下ka/kw不同时超孔隙气压力、超孔隙水压力及固结度随时间的变化规律.由图可以看出,梯形荷载作用下的变化规律与正弦荷载、三角形荷载作用下的变化规律类似.另外,在每个周期的中间段,均有一个带凹陷的“平台期”,而在“平台期”的两端各有一个凸起,这是由于土体黏滞性的存在,土中孔隙压力的消散尚未适应荷载的突变引起的.另外,ka/kw越大,超孔隙气压力和超孔隙水压力消散越快,土体固结速度越快.
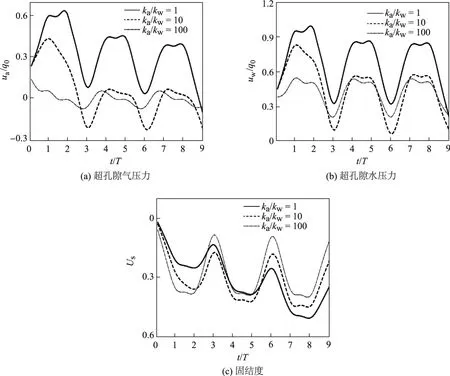
图9 梯形荷载作用下ka/kw不同时非饱和黏弹性地基的固结特性随时间的变化Fig.9 Change in consolidation characteristics of viscoelastic unsaturated soils for trapezoidal loading at diあerent values of ka/kw
4 结束语
本工作基于已有的非饱和黏弹性地基一维固结理论,应用Merchant黏弹性模型,运用Laplace变换和Cayley-Hamilton方法,求得了正弦荷载、三角形荷载和梯形荷载3种情况下的非饱和黏弹性地基一维固结时超孔隙气压力、超孔隙水压力以及土层沉降的解;然后,采用Crump及Durbin方法实现Laplace逆变换,获得了半解析解;最后,通过算例分析了3种循环荷载作用下非饱和黏弹性地基的一维固结特性.研究结果表明:①循环荷载作用下超孔隙气压力、超孔隙水压力和固结度的变化与荷载类似,呈周期性变化;②循环荷载作用下非饱和黏弹性地基固结时的超孔隙气压力和超孔隙水压力的变化规律基本相同,当ka/kw越大时,超孔隙气压力越快消散到0,超孔隙气压力和超孔隙水压力消散越快;③循环荷载作用下非饱和土黏弹性地基的固结过程中,ka/kw越大,固结速度越快;④循环荷载作用下超孔隙气压力、超孔隙水压力和固结度呈上下振动趋势,但从整体上看,变化曲线的中心线向下倾斜,超孔隙压力越来越小(一直在消散),而固结度越来越大(土体一直在固结).
[1]BLIGHT G E.Strength and consolidation characteristics of compacted soils[D].London:University of London,1961.
[2]SCOTT R F.Principles of soil mechanics[M].Massachusetts:Addison Wesley Publishing Company,1963.
[3]BARDEN L.Consolidation of compacted and unsaturated clays[J].Geotechnique,1965,15(3):267-286.
[4]FREDLUND D G,HASAN J U.One-dimensional consolidation theory:unsaturated soils[J].Canadian Geotechnical Journal,1979,17(3):521-531.
[5]FREDLUND D G,RAHARDjO H.Soil mechanics for unsaturated soils[M].New York:John Wiley and Sons,1993.
[6]王奎华,谢康和,曾国熙.双面半透水边界的一维黏弹性固结理论[J].岩土工程学报,1998,20(2):34-36.
[7]蔡袁强,徐长节,袁海明.任意荷载下成层黏弹性地基的一维固结[J].应用数学和力学,2001,22(3):307-313.
[8]蔡袁强,梁旭,郑灶锋,等.半透水边界的黏弹性土层在循环荷载下的一维固结[J].土木工程学报,2003,36(8):86-90.
[9]谢康和,周瑾,董亚钦.循环荷载作用下地基一维非线性固结解析解[J].岩土力学与工程学报,2006,25(1):21-26
[10]SHAN Z D,LING D S,DING H J,et al.Analytical solution for the 1D consolidation of unsaturated multi-layered soil[J].Computers and Geotechnics,2014,57:17-23.
[11]ZHOU W H,ZHAO L S.One-dimensional consolidation of unsaturated soil subjected to timedependent loading with various initial and boundary conditions[J].International Journal of Geomechanics,2014,14(2):291-301.
[12]LIEM H,BEHZAD F.Analytical solution for the two-dimensional plane strain consolidation of an unsaturated soil stratum subjected to time-dependent loading[J].Computers and Geotechnics,2015,67:1-16.
[13]QIN A F,CHEN G J,TAN Y W,et al.Analytical solution to one dimensional consolidation in unsaturated soils[J].Applied Mathematics and Mechanics(English Edition),2008,29(10):1329-1340.
[14]QIN A F,SUN D A,Tan Y W.Analytical solution to one-dimensional consolidation in unsaturated soils under loading changed exponentially with time[J].Computers and Geotechnics,2010,37(1):233-238.
[15]秦爱芳,罗坤,孙德安.非饱和土黏弹性地基一维固结特性分析[J].上海大学学报(自然科学版),2010,16(2):203-209.
[16]KORN G A,KORN T M.Mathematical handbook for scientists and engineerings[M].New York:McGraw-Hill Inc,1968.
[17]DURBIN F.Numerical inversion of the Laplace transforms:an eきcient improvement to Dubner and Abate’s method[J].The Computer Journal,1974,17(4):371-376.

