基于供应链金融的银企合作研究

张晓杰，余万林

在供应链金融环境下，市场需求的不确定性和产品价格波动会加剧商贸企业的运作风险和金融市场的融资风险。如2013年，钢材价格一落千丈和钢材市场信贷危机，使许多商贸企业陷入亏损或贷款逾期困境；2014年,由于煤炭、铁矿石、原油、大豆、黄金等大宗商品价格再现大幅下跌，各金融机构陆续通过增加抵押担保和减少借贷规模等方式防控大宗商品融资风险。与此同时，我国许多商贸企业，特别是中小商贸企业资金运作压力大，资金约束刚性强，在申请银行贷款过程中遇到抵押物价值低、交易成本高等难题。因此，企业融资过程中，如何既规避风险，又兼顾双方利益，实现银企之间合作关系双赢和银企资金供应链收益最优化，是亟需研究的问题。

从企业融资渠道来看，主要有金融机构（银行）融资、供应链内部融资、第三方物流企业融资等。我们研究的主要是银行提供融资方面的服务。目前，相关的研究工作主要有：Dada等利用报童模型，基于Stackelberg博弈理论，构建了银行与企业之间的线性和非线性契约模型［1］569－573；陈祥锋［2］70－77、Kouvelis 等［3］566－580在 Dada 等构建模型的基础上，增加了一个节点企业供应商，分析了企业从银行贷款和从供应商贷款的情景，研究结果表明最优的商业信用契约使得供应商和供应链的绩效得到提高；Jing等分析了在考虑信用合同的情况下，银行借贷的偏好问题［4］1090－1101；Srinivasa［5］407－412、Yan 等［6］1039－1058研究了供应链中供需双方都存在流动资金不足情况下需要向银行贷款时的决策问题；刘克宁等分析了市场价格信息不对称时，受资金约束的企业为获取最优订货量，从资本市场借贷的供应链运营和融资决策问题［7］647－655；刘红生等在利率市场化环境下，采取利息补贴承诺的方法，设计了一种以风险分担和收益共享为目的的契约机制，解决银行信贷资金的风险损失问题［8］205－211。在供应链契约协调研究方面，谢鑫鹏等利用收益共享寄售契约，分析了需求具有碳排放敏感性的低碳供应链的协调问题［9］107－115；张欢等利用批发价格契约以及销售奖惩契约，研究了双边信息不对称下供应链的协调问题［10］1570－1580；肖群等利用回购契约，分析了促销努力成本信息不对称下供应链的协调和优化问题［11］27－34。

在参考以上文献的基础上，在贷款利率市场化背景下以及产品市场需求与企业管理水平相关条件下，根据博弈理论和契约协调理论，构建了银企资金供应链成本共担和收益分成契约，通过Stackelberg模型研究了银行和企业在理性约束下的合作博弈行为，分析其各自的最优行动策略及对应的契约参数范围。

一、供应链金融模型的基本假设

选择相互独立的银行S和企业R形成两级资金供应链，并假定供应链的参与者是完全理性且风险中性的，均按照利润最大化原则做决策。资金市场价格，即利率是开放的，且利率、企业销售水平等信息对供应链的各参与方是对称的。作为资金提供方，银行是资金供应链的主导方，负责给出契约并提供契约参数。企业作为资金需求方，在资金供应链中的角色是参与方，根据契约参数确定其最优资金需求量。同时，银行可以获得必要的信息，推断企业需要的资金数量，从而制定最佳信贷决策。

假设产品销售水平X（e，ξ）与企业管理水平之间的关系为加法形式，X（e，ξ） =z（e，ξ） + ξ。其中 e，表示企业的管理水平，e≥0；z（e）为管理水平e下的销售绩效，为企业管理水平e的增且管理水平的边际效应递为独立于e的、表征产品需求的随机变量，其概率密度函数和分布函数分别为f（ξ）和F（ξ）。产品销售水平X（e，ξ）的概率密度函数和分布函数可分别记作f（x｜e）=f（x-z（e））和F（x｜e）=F（x-z（e））。g（e）表示企业在管理水平e下的管理成本，且g（0）=0，g’（e）＞0 和 g”（e）＞0。

银行的资金筹措成本为c，企业的融资成本为w。企业的产品产量为Q，单位产品的零售价格为p，营销成本为cr。在销售季末，剩余产品的单位处理价格v，且v＜cr。企业和银行从销售收入中获得收益比率为φ：1-φ，分担的管理成本比率亦为 φ：1-φ。

用 S（Q，e）表示销售量，则：

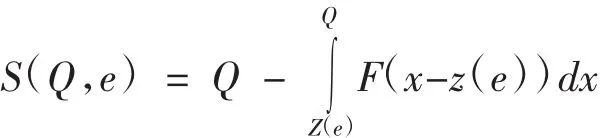
相应的处理产品量为：

二、供应链金融环境下银企合作博弈分析

（一）分散与集中决策模式下供应链收益分析

契约约束下的供应链管理，体现了供应链中各参与主体在个体理性假设下分散决策。此种模式下，企业的期望收益函数为：

求式（1）关于Q的偏导，

令式（2）等于 0，

将式（4）和 u=x-z（e）代入式（1），

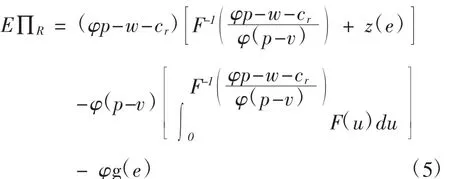
式（5）求关于e的偏导，

令式（6）等于0，可知，Q*和e*取决于z（e）、g（e）和随机变量ξ的分布。

将Q*和e*代入式（1）可得企业的最优期望收益函数：

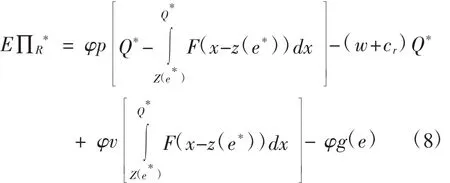
为实现各参与主体合作关系优化，在契约约束下的供应链收益应不低于上下游一体化管理、集中决策模式下的供应链收益。因此，有必要分析集中决策模式下，供应链的整体期望收益及相应条件。

集中决策模式下，供应链整体期望收益函数：

求式（9）关于Q和e的偏导，

令式（10）和（11）分别等于 0，

假定契约约束下供应链中各参与主体分散决策时，其收益总和可以达到集中决策模式下的供应链收益水平，即+=。此时，等式Q*=和e*=e~须成立。

由式（4）和式（12）得：将式（15）代入式（1），可得到融资成本下企业的期望收益函数为：

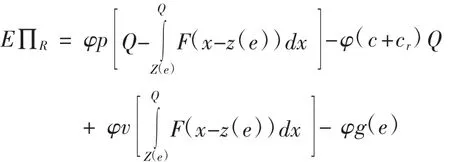
相应的银行期望收益函数为：

（二）契约约束下银企合作博弈分析

在契约约束的供应链分散决策模式下，企业作为资金需求方，在资金供应链中的角色是参与方，可独立于银行做出个体决策。作为资金的提供方，银行是资金供应链的主导方。为了使企业在追求自身收益最大化的同时实现整个供应链收益最大化，可通过给出契约并提供收益分成比率φ的方式，向企业提出风险分担和收益共享。

在供应链分散决策模式下，当银行提供资金的价格，亦即企业的融资成本w=w*时，企业的期望收益函数为：

相应的银行期望收益函数为：

求式（18）关于和的偏导，

令式（20）和（21）分别等于 0，可得：

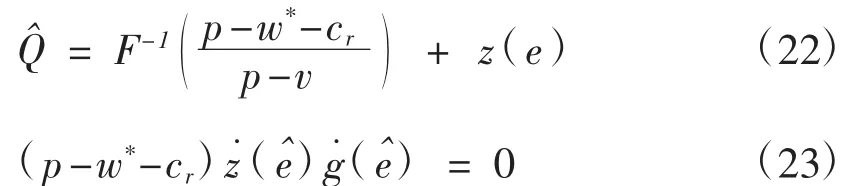
可见，Q^和e^取决于 z（e）、g（e）和随机变量 ξ的分布。当w*给定时，分散决策模式下的最优解（Q^，e^）为一类Stackelberg均衡状态。

将Q^代入式（20），将Q^，e^，w*，分别代入式（18）和（19），

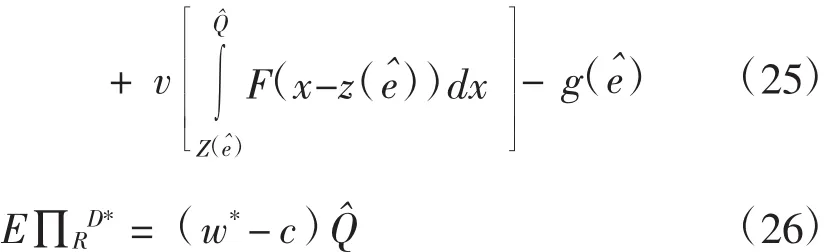
在个体理性假定下，供应链各参与方只有在满足自身利益的前提下，才会考虑整个供应链利益的最大化。因此，为了保证各方均能够接受契约的前提条件是：在该契约约束下各方的收益均是 Pareto 改进［12］18－25，换句话说，就是要保证在该契约约束下双方所获得的收益水平不小于分散决策下各自可获得的收益水平。上述条件可用以下两个不等式表示：

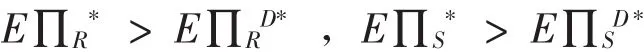
将式（16）、（17）分别代入上式可得：

因此，银行在设计收益分成契约时，只有将分成比率φ的取值限定于式（27）所确定的范围时，才能在保证自己收益水平的同时，让企业有意愿接受该契约。需要指出的是，分成比率φ的具体取值，将取决于银行和企业在资金供应链中的地位及相互之间的议价能力。

三、案例研究

假设某一城市商业银行和一家产品代理零售商构成银企供应链，该供应链中各参数如下：

设ξ满足A，［］

B 上的均匀分布，则：

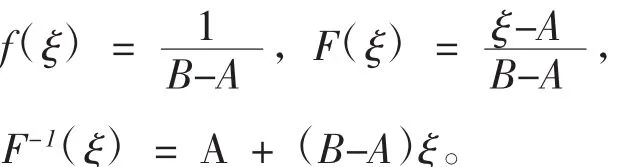
取 c=5，w=4，v=3，cr=1，p=15，A=5，B=100，a=100，w*=11，可得：

此时，分成比率φ的取值范围为：

0.3＜φ＜0.58 。

银行在向企业提供收益分成契约时，只要将分成比率φ限定在上述范围内，企业将会接受该契约。

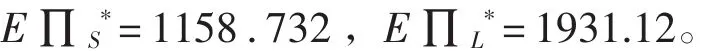
四、结语

在贷款利率市场化背景下，本文构建了银企资金供应链的收益分成契约模型，并通过Stackelberg模型研究银行和企业在理性假定下的合作博弈行为，分析了其各自的最优行动策略及对应的契约参数范围。分析表明，在供应链金融环境下，银企双方通过收益分成契约，实现了供应链参与各方决策的协调和合作关系的优化。

［1］Dada M，Hu Q.Financing newsvendor inventory［J］.Operations Research Letters，2008，36（5）.

［2］陈祥锋，朱道立，应雯珺.资金约束与供应链中的融资和运营综合决策研究［J］.管理科学学报，2008，11（3）.

［3］Kouvelis P，Zhao W H.Financing the newsvendor：Supplier vs bank，and the structure of optimal trade credit contracts［J］.Operations Research，2012，60（3）.

［4］Jing B，Chen X，Cai G G.Equilibrium financing in a distribution channel with capital constraint［J］.Production and Operations Management，2012，21（6）.

［5］Srinivasa Raghavan N R，Mishra V K.Short－term financing in a cash－constrained supply chain ［J］.Int J of Production Economics，2011，134（2）.

［6］Yan N，Sun B.Coordinating loan strategies for supply chain financing with limited credit［J］.OR Spectrum，2013，35（4）.

［7］刘克宁，宋华明.市场价格信息不对称的银企融资决策［J］.控制与决策，2016，31（4）.

［8］刘红生，李帮义.市场利率环境下银企信贷信息共享信号传递博弈模型［J］.运筹与管理，2015，（6）.

［9］谢鑫鹏，赵道致，刘永军.需求具有碳排放敏感性的低碳供应链收益共享寄售契约［J］.系统管理学报，2015，24（1）.

［10］张欢，刘洋.双边信息不对称下供应链契约研究［J］.计算机集成制造系统，2016，22（6）.

［11］肖群，马士华.促销努力成本信息不对称下供应链回购契约［J］.运筹与管理，2015，24（3）.

［12］郭福利.基于随机需求的供应链收益共享契约设计研究［D］.西安：西安理工大学，2008.