基于LS-SVM与GPC算法的锅炉燃烧优化控制

张仲琪1，付树强1，林 涛，李金京

(1.山西鲁能河曲发电有限公司，山西 忻州 036500；2.上海交通大学，上海 200240)

由于工业过程非线性对象的动态特性具有非线性、强耦合与大滞后的特点，非线性模型预测控制(nonlinear model predictive control，NMPC)是针对该类对象动态优化较为理想的控制方法。文献[1]基于支持向量机动态模型，分别采用随机搜索优化算法和遗传算法求解最优控制量。文献[2]提出了基于ε-SVM动态模型和神经网络模糊推理系统的非线性预测控制技术。文献[3]提出了基于数据挖掘算法建立系统非线性动态模型，进而采用模型预测控制算法和进化算法求解最优控制参数的动态优化控制方案。文献[4]运用Stirling插值公式对非线性系统模型进行线性处理，进而基于线性模型采用预测控制算法求解最优控制序列。文献[5]提出采用引入粒子滤波重采样步骤改进的粒子群算法，并与粒子的变异操作相结合来求解非线性模型预测控制优化控制律的方法。文献[6]提出将滤子法与一种信赖域SQP算法相结合的改进SQP算法，用于基于非线性Volterra模型的带控制约束的多步预测控制求解。文献[7]针对基于二阶Volterra模型描述的非线性系统，研究了带终端条件、输入输出约束和输入增量约束的非线性动态矩阵控制(dynamic matrix control, DMC)问题。Hammerstein模型是由非线性静态模型和线性动态模型串联构成，基于该类模型结构的动态优化问题常分解为线性模型的动态优化问题和非线性模型的静态求解问题。文献[8]与[9]基于Hammerstein模型结构的动态模型，分别采用预测函数控制PFC算法和动态矩阵控制算法(DMC)求解中间变量值，进而求解非线性p阶多项式模型得到控制器的输出。而文献[10]对于Hammerstein动态模型提出了基于混合神经网络的非线性预测控制算法。Wiener模型是另一种实验模型，其模型结构与Hammerstein模型类似，不同的是Wiener模型的线性动态环节在非线性静态环节之前。文献[11]基于在线训练的RBF神经网络与Laguerre函数相结合的方法，采用广义预测控制算法对Wiener型非线性系统的动态控制进行了研究。文献[12]研究了基于Wiener模型和TS-GA滚动优化算法的电站锅炉燃烧系统动态优化方案。

最小二乘支持向量机(least squares support vector machine, LS-SVM)是由Suykens提出的特殊支持向量机形式[7]。作为一种新颖的人工智能技术，LS-SVM算法在模式识别、系统建模、软测量、故障诊断和时间序列预测等多个领域均有广泛的应用[8]。

广义预测控制(GPC)是由克拉克(Clarke)等在保持最小方差自校正控制的模型预测、最小方差控制、在线辨识等原理的基础上，汲取动态矩阵控制(DMC)、模型算法控制(MAC)中的多步预测优化策略而提出的。它是对数学模型要求较低、鲁棒较强的自适应控制算法[13]。

本研究中融合最小二乘支持向量机算法高精度的非线性拟合能力和广义预测控制算法高性能的动态调节能力，提出LSSVM-GPC动态优化控制算法，以用于锅炉燃烧系统的动态优化实时调节与控制。

1 LS-SVM动态模型的在线线性化

(1)

根据LS-SVM模型训练原理，模型参数αT=[α1…αl]1×l与b通过式(2)求解

(2)

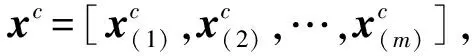
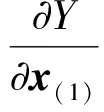
(3)

若令

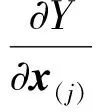
则式(3)又可写成式(4)，系数A(j)的求解如式(5)所示。

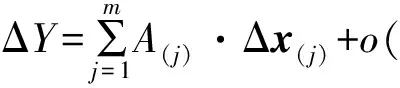
(4)

(5)

2 基于LS-SVM的CARIMA动态模型构建

在GPC算法中，对象动态模型采用的是受控自回归积分滑动平均模型(CARIMA)，模型结构如式(6)所示。其中A(q-1)=1+a1q-1+…+anq-n，B(q-1)=b0+b1q-1+…+bnbq-nb，Δ=1-q-1，可令C(q-1)=1。

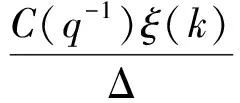
(6)

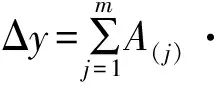
x= [{u1(k),…,u1(k-nb1)}，…， {um(k),…,um(k-nbm)}，{y(k),…y(k-n)}]

(7)

对于非线性被控对象，基于所建立的LS-SVM非线性动态模型构建CARIMA动态模型的过程可总结如下。

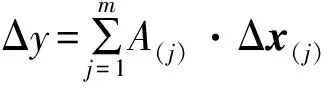
A(q-1)y(k+1)=B1(q-1)u1(k)+…+Bm(q-1)um(k)

(8)

其中

A(q-1)=1+a1q-1+…+anq-n，

至此，即完成了LS-SVM非线性动态模型向CARIMA线性预测模型的转换。

3 基于LS-SVM与GPC的动态优化控制算法

前面已经介绍基于LS-SVM全参数动态模型构建CARIMA动态模型的方法，基于CARIMA模型采用GPC求解最优控制律的动态优化算法可参考文献[15]。下面将上述算法进行结合，提出LSSVM-GPC动态优化控制方案。LSSVM-GPC动态优化控制方案的流程如图 1所示，图中Td是动态优化控制周期。对LSSVM-GPC动态优化控制方案的具体描述如下。

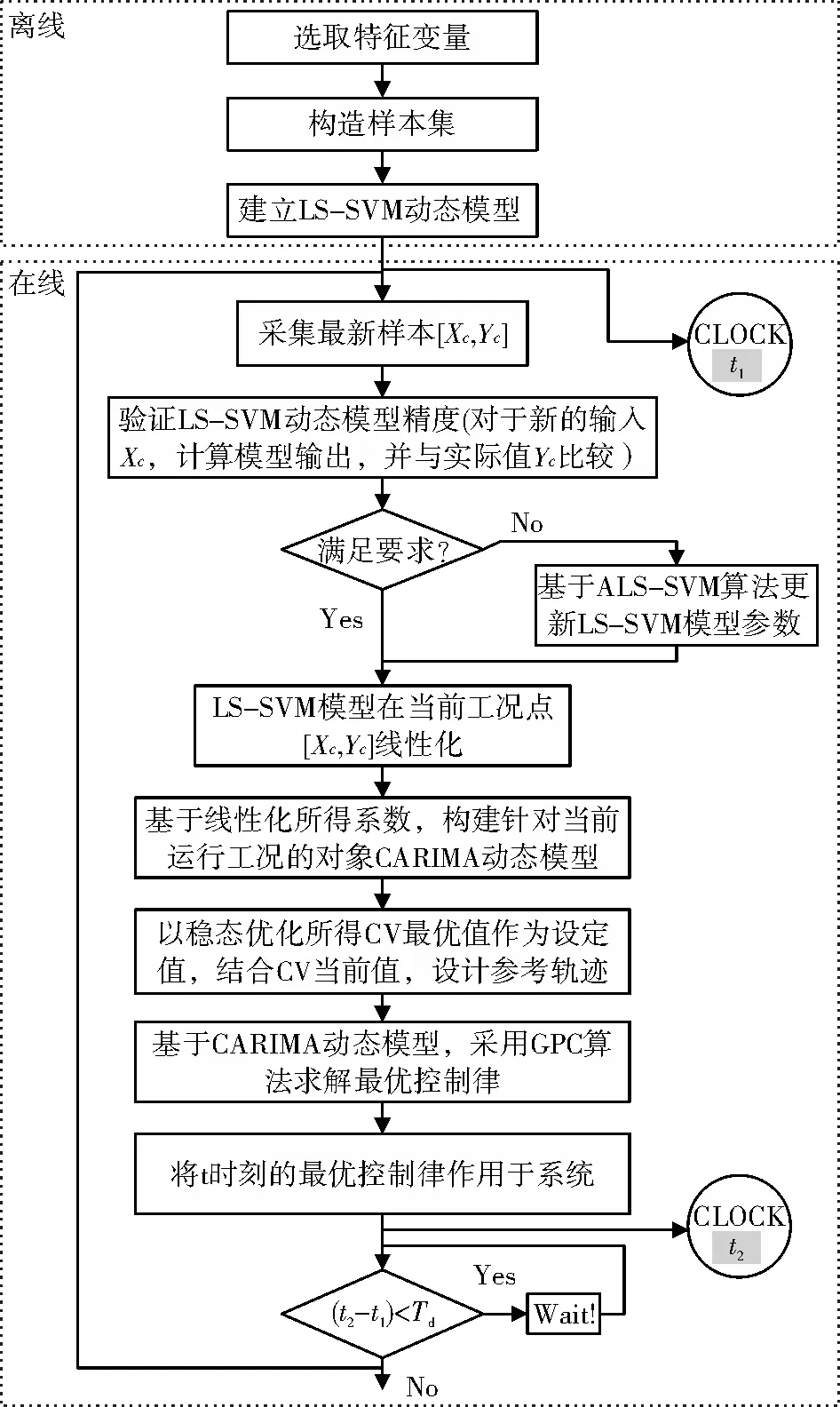
图1 基于LSSVM-GPC算法的动态优化控制流程

1)离线建模

第一步：选择特征变量，基于电厂历史运行数据，构建训练样本。

第二步：建立基于LS-SVM算法的电站锅炉燃烧系统全参数非线性动态模型。

2)在线运行

第三步：采集电站锅炉燃烧系统的最新运行数据，构建动态模型新的学习样本[Xc,Yc]。

第四步：对于最新输入Xc，验证LS-SVM动态模型的精度，若模型精度满足要求则转第六步，反之，转第五步。

第五步：利用新的样本[Xc,Yc]，基于ALS-SVM算法更新锅炉燃烧系统LS-SVM动态模型参数。

第六步：LS-SVM动态模型可以拟合当前锅炉燃烧系统的动态特征，在当前工况点[X,Yc]将LS-SVM动态模型在线线性化。

第七步：基于LS-SVM模型线性化后所得系数，构建电站锅炉燃烧系统的实时CARIMA线性动态模型。

第八步：以稳态优化所得被控变量的最优值为设定值，结合被控变量的当前值，设置其未来P时间段内的参考轨迹，并对动态优化问题的约束条件进行处理。

第九步：基于CARIMA线性动态模型，采用带约束的GPC算法求解最优控制律。

第十步：将所得最优控制律中t时刻的控制量(如烟气含氧量设定值、各层二次风门开度、磨煤机的容量风门开度偏置等)作用于电站锅炉燃烧系统。

第十一步：在动态优化周期到达时，返回第三步。

4 算法验证

4.1 仿真算例

为验证上述LSSVM-GPC动态优化方案的控制效果，以某特征已知、带延迟的2I2O非线性对象为例进行仿真试验，对象的动态特性描述如式(9)所示。

(9)

假设系统初值为u1(0)=u2(0)=0,y1(0)=1.516,y2(0)=1.378 8，为稳定状态。仿真试验中同样研究当设定值变为y1_sp=4,y2_sp=2时，系统的跟踪能力，以及在系统达到新的稳态后，加入Δ=0.5的扰动于输出侧，观察系统的抗干扰能力。控制器参数的设计为：预测时域P=4；控制时域M=2；输出跟踪偏差加权系数项q=[q1,q2]=[1,0.9]；控制能量项加权系数λ=[λ1,λ2]=[0.1,0.1]；参考轨迹柔化因子α=[α1,α2]=[0.6,0.5]。为缩短动态调节时间，该动态优化方案中也采用变尺度优化策略，根据被控变量与给定值间的偏差缩小Δu的优化范围。

图2验证了LSSVM-GPC算法的动态优化控制效果。在[0,30Td]系统表现出了对给定值良好的快速跟踪能力；当t=30Td系统达到新的稳态后，在输出部分加入幅值为0.5的扰动量，系统被控变量会出现振荡，但在控制器作用下仍可以快速地调节至给定值，说明LSSVM-GPC算法具有很好的抗干扰能力。另外，在计算时间方面，本仿真算例中，基于LSSVM-GPC算法的最优控制策略平均求解时间仅为0.051 4 s，远远少于LSSVM-GA动态优化算法，非常适合在线工业过程调节。

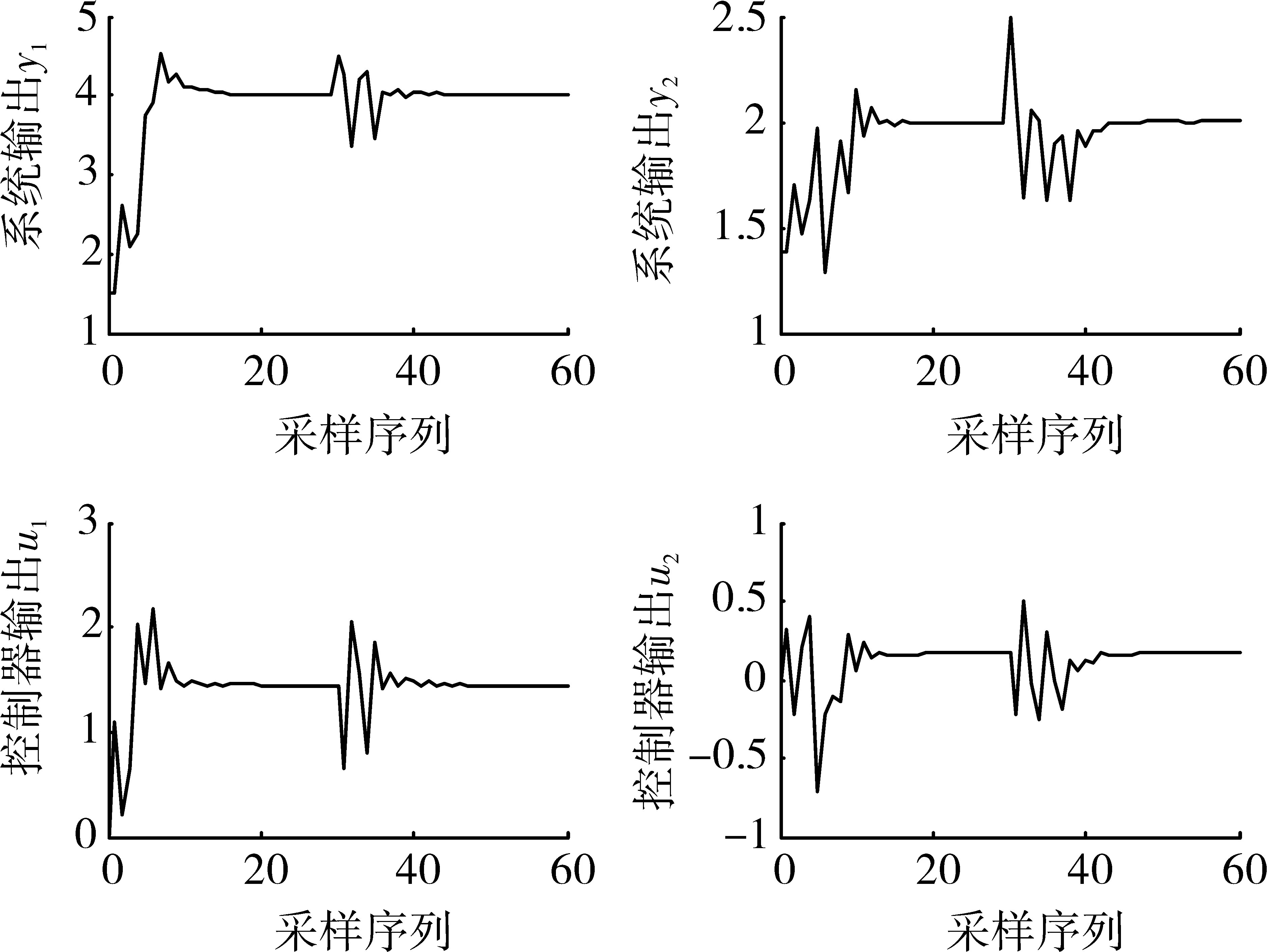
图 2 LSSVM-GPC动态优化算法的性能验证程

4.2 LSSVM-GPC算法的动态燃烧优化结果

假设某电站锅炉燃烧系统LS-SVM全参数动态模型，在线线性化后所构造的CARIMA预测模型参数如表1所示。

表1 CARIMA预测模型构建参数对照表

通过对锅炉燃烧系统运行机理的分析可知，负荷、入炉煤的热值和环境温度是影响锅炉效率的主要扰动变量；烟气含氧量作为送风量校正回路的被调节量，决定了燃烧过程中风煤比，也是影响锅炉效率的主要因素；一次风压、各层二次风门开度和各层燃尽风门开度表征了锅炉燃烧过程中的配风方式，而各层磨煤机的容量风门开度偏置代表了总煤量沿炉膛高度的分配情况，它们都对飞灰含碳量、污染物排放量等具有一定的影响。根据电站锅炉的历史运行数据，通过采用统计学方法分析，锅炉排烟温度动态模型的输入包括load(k)、Qar(k)、Tlk(k)、O2(k-2)、O2(k-1)、PA(k-2)、PA(k-1)、OFA_A(k-2)、OFA_A(k-1)、OFA_B(k-2)、OFA_B(k-1)、MA_b(k)、MB_b(k)、MC_b(k)、MD_b(k)、ME_b(k)和Tpy(k)，共17维，模型输出为Tpy(k+1)。其中模型输入load(k)为k时刻的机组负荷，Qar(k)为k时刻的入炉煤的热值，Tlk(k)为k时刻的环境温度，O2(k-2)为k-2时刻的烟气含氧量，O2(k-1)为k-1时刻的烟气含氧量，PA(k-2)为k-2时刻的一次风压，PA(k-1)为k-1时刻的一次风压，OFA_A(k-2)为k-2时刻的A层燃尽风门开度，OFA_A(k-1)为k-1时刻的A层燃尽风门开度，OFA_B(k-2)为k-2时刻的B层燃尽风门开度，OFA_B(k-1)为k-1时刻的B层燃尽风门开度，MA_b(k)、MB_b(k)、MC_b(k)、MD_b(k)和ME_b(k)为k时刻的各磨煤机的容量风门开度偏置，Tpy(k)为k时刻的排烟温度。锅炉NOx排放量动态模型的输入包括load(k)、Qar(k)、Tlk(k)、O2(k-3)、O2(k-2)、PA(k-3)、PA(k-2)、OFA_A(k-3)、OFA_A(k-2)、OFA_B(k-3)、OFA_B(k-2)、MA_b(k)、MB_b(k)、MC_b(k)、MD_b(k)、ME_b(k)和NOx(k)，也共17维，模型输出为NOx(k+1)。上述参数中O2(k-3)为k-3时刻的烟气含氧量，PA(k-3)为k-3时刻的一次风压，OFA_A(k-3)为k-3时刻的A层燃尽风门开度，OFA_B(k-3)为k-3时刻的B层燃尽风门开度，NOx(k)和NOx(k+1)分别为k和k+1的锅炉NOx排放量，其余参数定义与排烟温度模型相同。由于配煤方式无需时刻变化，因此不将其作为动态燃烧优化控制模块的调节变量，此时五层磨煤机的容量风门开度偏置(MA_b、MB_b、MC_b、MD_b与ME_b)相当于扰动变量，表1中动态优化中的调节变量只包括烟气含氧量O2、一次风压PA、两层燃尽风门开度(OFA_A和OFA_B)，模型输出为排烟温度Tpy和烟气中NOx含量。

假设机组初始运行于负荷为483 MW的稳态工况，初始工况下，锅炉燃烧系统各被控变量如表2所示；稳态优化得到的当前工况下各被控变量可达到的最优目标值也列于表2中，表中锅炉效率计算方法参考文献[17]。以稳态优化所得最优被控变量为给定值，基于前面所提出的LSSVM-GPC算法，求解从当前工况向最优工况动态调节过程中的最优操作变量。

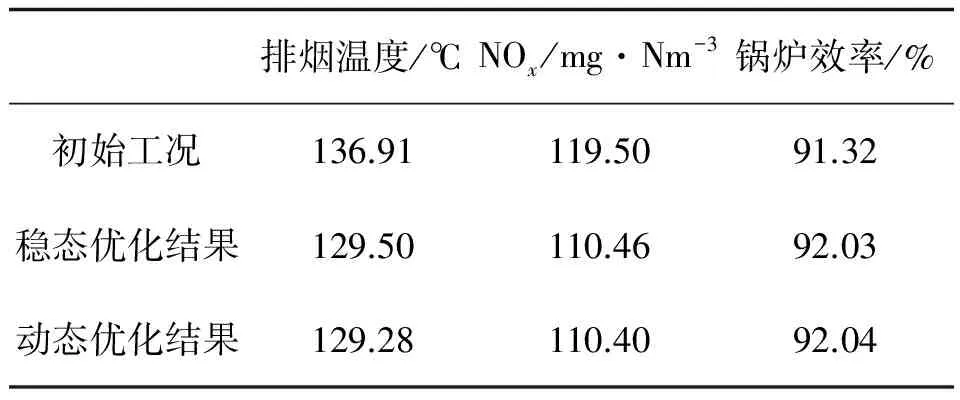
表2 基于LSSVM-GPC的动态燃烧优化结果

图3列出了动态过程中各操作变量的调节曲线，图4所示为被控变量Tpy和NOx排放量的动态变化轨迹；表 2列出了动态优化结束后锅炉燃烧系统各被控变量的最终值。表中数据显示LSSVM-GPC动态优化控制后的稳定工况与稳态优化模块所得的最佳工况接近，且从图中CVs和MVs的动态变化轨迹可看出，该动态优化控制算法具有较佳的动态调节性能。

图3 LSSVM-GPC动态燃烧优化中的操作变量

图4 LSSVM-GPC动态燃烧优化中的被控变量变化轨迹

5 结论

本文基于LS-SVM的强非线性拟合能力，提出了建立对象的LS-SVM全参数动态模型，并研究了非线性LS-SVM动态模型在线线性化和实时CARIMA线性动态模型的构建方法，进而提出了基于LSSVM-GPC算法的快速动态优化控制方案。文中仿真试验结果表明所提出LSSVM-GPC动态优化控制算法具有较好跟踪能力和抗干扰能力，可用于工业过程的实时调节。

[1] 徐保国，胡立萍．基于支持向量机的非线性系统模型预测控制[J]．计算机测量与控制，2005，13(8):799-801．

[2] IPLIKCI S.Support vector machines based neuro-fuzzy control of nonlinear systems [J]. Neurocomputing, 2010, 73:2097-2107．

[3] SONG Z, KUSINK A. Optimization of temporal processes: a model predictive control approach [J]. IEEE Transactions on evolutionary computation, 2009, 13(1):169-179.

[4] 盖俊峰，赵国荣，周大旺．一种基于线性近似的非线性系统模型预测控制方法[J]．航天控制，2015,33(5)：3-7．

[5] 赵婷婷，程奇峰，王志丰．改进粒子群算法优化的非线性模型预测控制[J]．辽宁工程技术大学学报(自然科学版)，2015,34(4)：517-522．

[6] 贺静，赵众，董叶伟．基于Volterra模型的预测控制及应用[J]．控 制 理 论 与 应 用，2015,32(3)：312-319．

[7] GENEELI H, NIKOLAOU M．Design of robust constrained model-predictive controllers with Volterra series．AIChE J, 1995, 41(9):2 098-2 107．

[8] 张泉灵，王树青．基于Hammerstein模型的非线性预测函数控制[J]．浙江大学学报(工学版)，2002，36(2)：119-122．

[9] 邹志云，于德弘，郭宁，等．一种新型非线性Hammerstein系统动态矩阵控制算法[J]．计算机与应用化学，2008，25(4):432-436．

[10] 向微，陈宗海，盛捷．具有Hammerstein模型描述的非线性系统的基于混合神经网络的预测控制[J]．控制理论与应用，2008，25(5):857-861．

[11] 李超璟，熊伟丽，徐保国．Winner型系统基于神经网络的在线训练算法广义预测控制[J]．内蒙古大学学报(自然科学版)，2003，34(2):216-220．

[12] 张毅．电站锅炉燃烧优化控制理论及应用研究[D]．北京：清华大学，2006．

[13] SUYKENS J A K, VANDEWALLE J．Least squares support vector machine classifiers[J]．Neural Processing Letters, 1999, 9(3): 293-300．

[14] 顾燕萍，赵文杰，吴占松．基于最小二乘支持向量机的电站锅炉燃烧优化[J]．中国电机工程学报，2010,30(17)：91-97．

[15] 席裕庚．预测控制[M]．北京：国防工业出版社，1993．

[16] GU Y,ZHAO W,WU Z．Online adaptive least squares support vector machine and its application in utility boiler combustion optimization systems[J]．Journal of Process Control, 2011, 21(7):1 040-1 048.

[17] 张小桃，王培红．一种新的锅炉效率的计算模型[J]．电站系统工程，1999，15(4):16-17．