中低速磁浮列车位置信号检测算法研究

戴春辉，谭 磊，龙志强，*，谢云德

(1. 国防科技大学，长沙 410073; 2. 北京控股磁悬浮技术发展有限公司，北京 100000 )

磁浮列车作为一种新型的轨道交通工具，越来越受到世界各国的关注。在中国上海已经建成了世界首条高速磁浮列车商业运营线。目前一条用于城市轨道交通的低速磁浮列车运营线(北京S1线)也正在积极施工建设中。对于采用异步直线电机的低速磁浮列车来说，速度反馈信号是其进行直线电机牵引控制的一个必要条件；对于采用同步直线电机的高速磁浮列车，与长定子磁极相位相对应的位置信号也是其能够实现同步牵引控制的基础[1-3]。

图1 中国自行研制的CMS04磁浮列车Fig.1 Self-made maglev train in China

然而，电磁型磁浮列车在运行时，悬浮于轨道上方约8 mm，与轨道无任何接触，因此传统轮轨列车定位测速码盘无法应用于磁浮列车系统。上海高速磁浮列车(SMT)采用直线同步电机牵引，同步电机的长定子沿轨道安装，由硅钢叠片压制成齿槽结构，并将牵引电缆镶嵌于长定子沟槽内，其车地相对位置可以通过车载电感式传感器来检测。美国通用原子能(General Atomics,简称GA)研制的磁浮列车采用双层Halbach结构的永久磁铁来实现EDS悬浮和同步直线电机牵引，它安装有激光测速系统，通过检测固定于轨道上的光学胶带(印有黑白相间的条纹)进行速度和位置检测，它采用450 MHz的无线电作为车地通讯的方式，从而将激光传感器采集的位置信息发送到地面牵引逆变控制单元。在低速磁浮领域，日本的HSST磁浮列车系统同样采用感应环线技术进行位置和速度检测，HSST磁浮列车系统在轨道中央铺设了周期性交叉的感应环线，内部通有一定频率的激励型号，再通过车载的3个接收天线接收地面感应环线内的信号并进行组合，通过测得位置脉冲的频率即可计算出列车运行速度。

本文采用基于交叉感应环线的定位测速方法，提出利用车载接收信号的包络微分来实现列车相对位置的检测，并着重解决了由于低速磁浮列车震动、电机干扰等导致的定位信号失真问题。

1 感应环线相对定位系统设计

1.1 地面环线系统设计

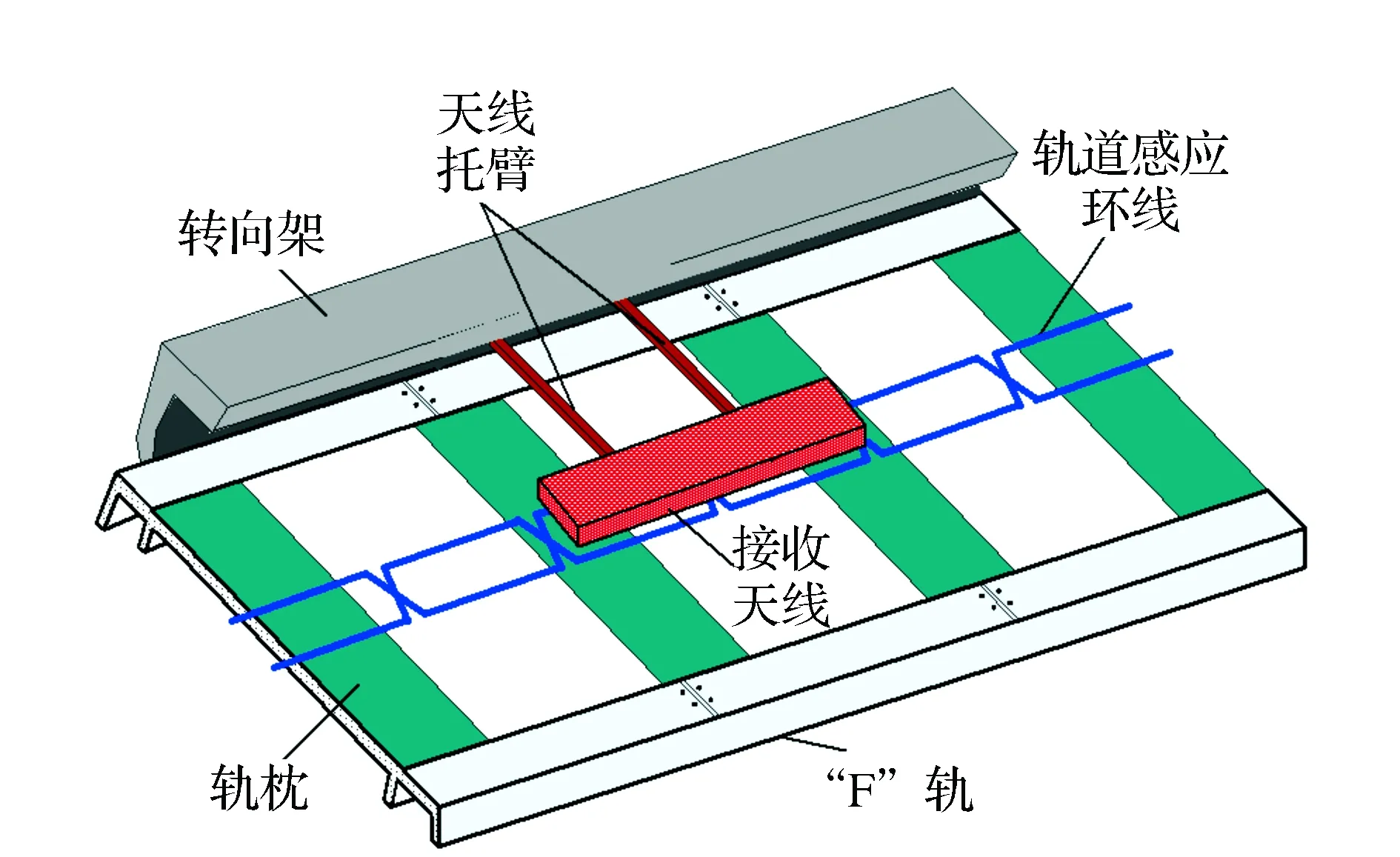
图2 交叉感应环线定位系统示意图Fig.2 Sketch map of positioning system using the loop-cable

地面环线定位系统主要由轨道交叉感应环线、环线信号驱动器以及终端阻抗匹配电路3部分组成，交叉感应环线由两条间距10 cm的平行导线每隔30 cm交叉一次铺设而成，具有交叉结构的感应环线铺设在轨道中央，车载接收天线通过托臂安装在列车转向架上，见图2。当感应环线内注入一定频率的正弦波信号时，车载天线可感应到同频率的信号，且信号幅值随列车运行的相对位置的变化而改变，通过提取接收信号幅值特征可对列车的相对位置和运行速度进行测量[4-5]。

环线信号驱动器用于给地面交叉感应环线提供频率为50 kHz的正弦信号激励。其主控MCU用于配置DDS信号发生器的相关参数，DDS信号发生器采用集成芯片AD9833，当AD9833使用1 MHz有源精准晶振时，其频率分辨率可达0.004 Hz。AD9833内部的DA转换器输出峰-峰值约为600 mV的正弦信号。

1.2 接收信号处理方法设计

由于地面交叉感应环线的特殊结构，由电磁场分析可知，环线正上方的接收天线接收到的信号最强，而在交叉点处信号最弱，理想情况为零。因此，当磁浮列车以一定的速度在交叉感应环线上方运动时，天线的接收信号应呈包络状，见图3。由图3可见，接收信号的包络经历了最小值到最大值变化的周期性过程。传统的处理方法是通过设计阈值比较电路，获得窄脉冲信号，从而提取环线交叉点的位置，由于接收线圈过交叉点幅值易受到天线振动和晃动等因素的影响，导致幅值信号存在抖动，如果阈值比较时无法进行相应地调整，可出现交叉点漏检的情况。而将阈值变大，可以增强过交叉点的检测能力，但是其占空比出现漂移，同样使列车位置和速度计算出现偏差。因此笔者考虑通过提取包络信号微分的方法，即通过检测包络信号的单调性提取列车运行的相对位置，可解决漏检的问题，提高了系统可靠性，检测方法见图4。

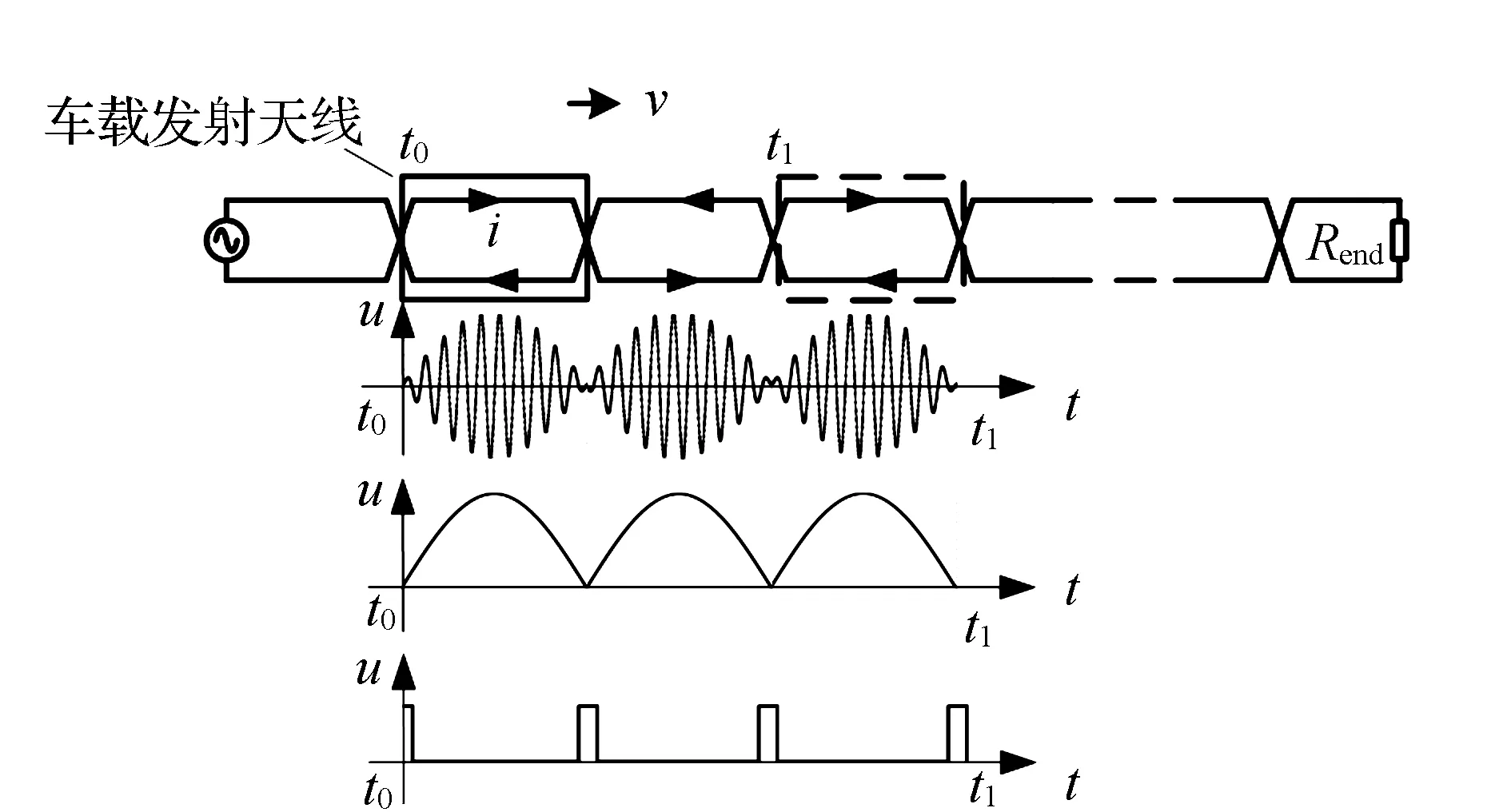
图3 基于阈值比较的位置信号提取方法Fig.3 Position signal extraction method based on threshold comparison

图4 基于包络信号微分的位置信号提取方法Fig.4 Position signal extraction method based on envelope signal differentiation

2 离散跟踪微分器的在系统中应用

2.1 定位信号失真原因分析

列车接收线圈的接收信号会因一些外界因素而产生失真，这些因素给后续的信号处理造成了一定的难度。定位接收线圈被安装在磁浮列车转向架上，而转向架上还安装有悬浮电磁铁、异步牵引直线电机等大功率电气设备，对定位线圈的接收信号质量产生影响,见图5。从上文介绍的磁浮列车定位原理可知，磁浮列车的位置信息是需要实时输出的，这种噪声使DSP在把实时采集的数据与标定的标准表格比照时出现较大误差，使实时位置发生错误；另外，由于一个周期的包络信号内呈对称分布，即分为递增区间与递减区间，为了将采样值转换为实际位置信号，需要区分采样值所处的信号区间，并根据离线标定的采样值-位置对照表格获取周期内的相对位置信号[6]。本文采用的方法是利用微分信号来进行有效区分，经典的微分提取算法是利用惯性环节有延迟地跟踪输入信号来获取近似微分，但是存在噪声放大作用，在本文所研究的存在较大电磁场干扰噪声的定位测速系统中并不适用。离散非线性跟踪微分器具有无超调、无颤振、快速跟踪输入信号、无需存储历史数据、实时性好、滤波效率高以及能获取适当微分的能力，不需要考虑复杂的系统建模，且易于工程应用，因而能够应用于本文所研究的定位测速系统中。

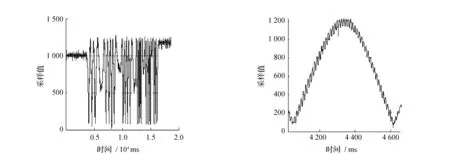
图5 高频噪声导致波形失真Fig.5 Waveform distortion caused by high frequency noise

2.2 二阶离散跟踪微分器介绍

韩京清等提出了一种跟踪微分器的思想，它是基于二次时间最速系统提出的一种离散形式的跟踪微分器，能够很好地解决颤振问题，无超调地跟踪输入信号，得到较好的微分信号，这种跟踪微分器应用于多种系统的自抗扰控制器中[7-11]。谢云德、龙志强提出了一种高精度的跟踪微分器，能够无超调、无颤振地跟踪输入信号，并获取良好的微分信号。这两种微分器的构造方式不同，前者是基于TD非线性区域的边界变换以及可达区，后者是基于开关曲线以及原点的到达时间的判断。从精确性的角度来讲，后者的判断条件是非常严格的，在时间节点上不存在任何的误差，而边界变换法在对应的线性区域内仅是一个大致的判断，个别点一步可达边界上的点除外。在两步可达区域内，需要两步才能到达原点，而文献[12]中的方法仅一步就能到达[12-14]。

结合文献[11]，基于时间判据的TD其离散化的形式可以表示为：

其中h为采样步长，k为离散化的步长数，r为快速因子，b(k)为修正项。

2.3 跟踪微分器的滤波特性分析

为了比较跟踪微分器对信号的跟踪以及微分特性，需要了解在所有可能的频段上的幅频、相频特性，而跟踪微分器是非线性的，不存在线性系统特有的传递函数的特性，因而无法用常规的频率响应法得到其Bode图，只能用频率扫描的方法获取相应的频率特性。由于跟踪微分器在经过参数选择后，能够稳定地跟踪谐波信号，因而可采用频率扫描的方法，拟合跟踪微分器的幅频和相频曲线，以研究其频域特性。

为了分析跟踪微分器滤波因子c0对算法输出特性的影响，本文使用了扫频算法，算法描述如下：

对于一个开环系统，假设其输入信号为单位正弦信号v(t)=sin(wt)，其输出可表示为：

y(t)=Asin(wt+φ)=[sin(wt),cos(wt)][Acos(φ),Asin(φ)]T

(1)

其中，变量A和φ分别表示输出信号的幅值和相位。

若在时域范围内取t=0,h,2h,…,nh，并取：

YT=[y(0),y(1h),y(2h),…,y(nh)]

(2)

(3)

d1=Acos(φ),d2=Asin(φ)

(4)

则有：

Y=Φ·[d1,d2]T

(5)

根据最小二乘原理，可以求出d1和d2的最小二乘解为：

(6)

因此，根据式(1)和式(6)，可求出在输入信号角频率为ω的前提下，系统输出信号的幅值和相位如下：

(7)

利用上述方法，选取角频率序列{ωi},i=1,2,…,n，对于每个频率点可求出其相应的输出信号幅值和相位(图6)，从而可拟合出跟踪微分器的幅频和相频曲线。

图6 滤波因子不同时相频和幅频曲线Fig.6 Phase frequency and amplitude frequency curve of different c0

由图6可见，随着c0的增大，算法的幅值和相位均出现不同程度的衰减和滞后，即c0越大，滤波效果越好，但相位滞后越大。

3 基于在跟踪微分器的相对定位系统实验

图7 跟踪微分器滤波处理前后Fig.7 Comparison of before filtering and after filtering

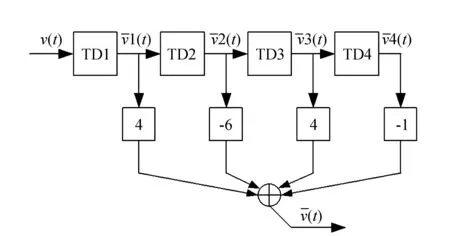
图8 跟踪微分器组算法框图Fig.8 Block diagram of tracking differentiator

因此，为了解决降噪和延迟之间的矛盾，本文选择采用跟踪微分器组的方案。跟踪微分器组是指在一个系统内将多个跟踪微分器进行串联，即通过将前一级跟踪微分器的输出作为后一级跟踪微分器的输入信号，输入信号通过若干级滤波处理后，输出信号可以很好地对输入信号进行滤波，从而解决了单个跟踪微分器滤波能力有限的问题。

若一个跟踪微分器的滤波延迟为τ，那么引入多个跟踪微分器将会带来更大的时间延迟。为了解决时间延迟问题，需要进一步引入相位补偿信号。

基于4阶跟踪微分器的滤波和微分信号提取原理框图见图8。TD1、TD2、TD3、TD4构成一个跟踪微分器组，这种串联的结构可以减小滤波后波形以及提取微分信号的相位延迟[15-16]。

利用补偿算法对接收线圈接收到的包络信号进行处理，得到的波形见图9。由图9可见，补偿算法时间延迟更小，且滤波效果理想。事实上，由2.2节的结论可知，磁浮列车与交叉感应环线相对位置区间的判断并不需要关心微分信号值的大小，而仅需要确定接收线圈处于感应环线正上方(此时接收信号幅值最大)还是交叉点上方即可(此时接收线圈接收到的信号幅值最小)，在两个位置之间的信号呈单调递增或递减变化，因此只要确定包络微分信号的符号为正或负即可判别出列车的相对位置。将接收线圈获得的微分信号做阈值比较，当微分信号>0时，输出高电平，反之，输出低电平信号，即可得到图10所示的方波信号，每次信号的反转即表示列车行进了15 cm。

图9 单跟踪微分器滤波与跟踪微分器组滤波输出比较Fig.9 Comparison of single tracking diffentiatior and tracking differentiator group

图10 微分信号与过零比较处理后的信号Fig.10 Differential signal and zero crossing signal after comparison processing

由图10可见，微分信号过零点附近存在波动，导致过零处理后的值过于敏感，抗干扰能力差。为了增强过零比较惯性，滤波算法中增加带滞回功能的数字比较器后得到的波形见图11。由图11可见，方波信号的跳变被有效消除。

图11 微分信号与过零滞回比较处理后的信号Fig.11 Differential signal and zero crossing hysteresis signal

4 结 论

新型跟踪微分器的思想来自于最优控制理论中的最小时间系统，是一种最快速的离散跟踪微分器。实验结果表明，这种滤波算法可实时快速跟踪输入信号的低频分量，滤除信号中的高频干扰成分，并且具有很小相位延迟。因此该算法可在强干扰信号中提取出平滑的微分信号。本文设计的磁浮列车相对定位系统，利用跟踪微分器滤波算法得出的跟踪信号以及微分信号,实现了列车相对位置的计算，得到了较好的效果。

[1] Zhang D, Long Z, Xue S，et al.Optimal design of the absolute positioning sensor for a high-speed maglev train and research on its fault diagnosis[J].Sensors,2012,12(8):10621-10622.

[2] Wu J, Zhou W,Li L.Research on speed and position detection system of high speed maglev train[J].Journal of national university of defense technology, 2011,33(1):109-114.

[3] Long Z, Ren Y, Liu S,et al.Speed and position detection system for maglev train based on inductive line intersected[J].Journal of Transducer Technology, 2001,20(7):51-55.

[4] Tan L, Dai C, Luo G, et al. Research on signal processing problems based on particle filter for medium-speed maglev train location and speed detection system[C]//The Chinese Control Conference,2017:5202-5206.

[5] Dai C. Analysis of impedance characteristics for the loop-cable position and speed detection system[C]//The Chinese Control Conference,2017:815-820.

[6] 张大鹏.基于无线感应的车地通信及测速定位系统研究[D].长沙：国防科技大学,2014.

[7] Han J Q, Yuan L L. The discrete form of a tracking-differentiator[J]. J.systems Sci.math.sci, 1999(3):268-273.

[8] 李军, 朱亚清, 陈文,等. 一种新型正弦跟踪微分器的研究与应用[J]. 控制理论与应用, 2016, 33(9):1182-1192.

[9] Bu X, Wu X, Zhang R, et al. Tracking differentiator design for the robust backstepping control of a flexible air-breathing hypersonic vehicle[J]. Journal of the Franklin Institute, 2015, 352(4):1739-1765.

[10] Bu X, Wu X, Tian M, et al. High-order tracking differentiator based adaptive neural control of a flexible air-breathing hypersonic vehicle subject to actuators constraints[J]. Isa Transactions, 2015, 58:237.

[11] 张帆, 徐华中, 向云,等. 针对含噪信号的自适应跟踪微分器改进研究[J]. 电光与控制, 2017(3):60-63.

[12] 谢云德，龙志强. 高精度快速非线性离散跟踪微分器[J]. 控制理论与应用，2009，26(2)：127-132。

[13] 窦峰山, 何洪礼, 谢云德,等. 基于跟踪微分器的磁浮列车定位测速系统信号处理问题研究[J]. 铁道学报, 2016(1):81-85.

[14] Xie Y, Long Z, Li J. Analysis of the second-order nonlinear discrete-time tracking-differentiator as a filtering[C]// Information Computing And Automation:(In 3 Volumes). 2015:785-789.

[15] Dai C, Long Z, Xie Y,et al.Research on the filtering algorithm in speed and position detection of maglev trains[J].Sensors, 2011,11(7):7204-7218.

[16] Dou F S, Dai C H, Xie Y D. Filtering algorithm and direction identification in relative position estimation based on induction loop-cable[J]. Journal of Central South University,2016, 23(1):112-121.