开关电感型Z源三电平逆变器直流链电压控制研究

王晓刚，张杰

（广州大学机械与电气工程学院，广东广州510006）

三电平中点钳位式（neutral point clamped，NPC）逆变器具有开关器件电压应力为两电平逆变器的一半、开关频率低等优点，因此在大功率场合得到广泛的应用[1-4]。但与两电平逆变器一样，三电平逆变器的拓扑本质上仍为降压型，因此需要较高的直流侧电压。Z源逆变器由彭方正提出[5]，在直流电源和常规三相两电平逆变器之间加入由电感、电容和二极管组成的阻抗网络，结合对逆变器的直通控制，使阻抗网络输出至桥式电路的电压（直流链电压）提升。将Z源阻抗网络引入三电平逆变器也可形成多种三电平拓扑，如单Z源三电平NPC逆变器[6]、双Z源三电平NPC逆变器[7]、Z源级联三电平NPC逆变器[8]、基于开关电感的三电平NPC逆变器[9]等，其中开关电感型（switched-inductor，SL）Z源三电平NPC逆变器（文中简称SL型Z源三电平逆变器）可以获得更高的升压因子。文献[10-12]研究了单Z源三电平逆变器的空间矢量调制方法，文献[13-15]研究了单Z源三电平逆变器的中点电位平衡控制方法，文献[16]研究了单Z源三电平逆变器的自适应控制，但是用全控器件替换了Z源阻抗网络中的二极管，增加了逆变器中开关器件的数量。目前还没有SL型Z源三电平逆变器直流链电压控制策略的文献。

与Z源两电平逆变器类似，SL型Z源三电平逆变器的直流链电压同样为高频脉动电压，其高电平峰值的恒定与否对逆变器的交流输出有决定性影响。通过直接设置直通占空比控制直流链电压属于开环控制方式，缺点是稳态误差大、动态性能不理想，因此有必要对直流链电压采取闭环控制。因直流侧电路具有非线性特性，常规线性控制将难以获得优良的性能。滑模控制是一种非线性控制方法，用于控制非线性多变量系统。滑模控制器对输入和参数扰动表现出良好的稳定性和鲁棒性。电力电子开关变换器为典型的开关非线性系统，适合采用滑模控制，这方面的研究多见于文献报道[17-21]。作者曾将滑模控制用于Z源两电平逆变器的控制[22]，获得优良的控制效果。

本文提出一种SL型Z源三电平中点钳位式逆变器的直流链电压滑模控制方法，研究直流侧建模和控制器的设计，分析控制器的稳定性，最后利用仿真对比施加滑模控制前后的稳态和暂态波形，验证控制器的有效性和优越性。

1 SL型Z源三电平逆变器的基本原理

SL型Z源三电平中点钳位式逆变器的主电路如图1所示。与常规三电平钳位式逆变器相比，直流电源和桥式电路之间增加了由2个开关电感及2个电容C1和C2构成的对称式X型阻抗网络，其中上侧开关电感由电感L1、L2，二极管D1、D2和D3组成；下侧开关电感由电感L3、L4；二极管D4、D5和D6组成。阻抗网络的作用是实现直流侧电压的提升，即逆变桥的输入电压（直流链电压）uin大于直流电源电压udc，这一点与Z源两电平逆变器相同。

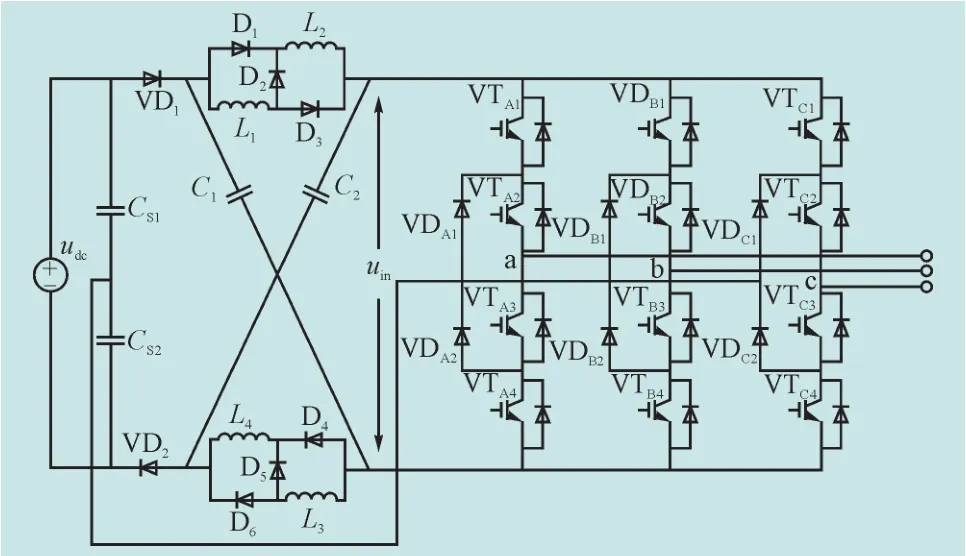
图1 SL型Z源三电平逆变器Fig.1 The switched-inductor Z-source three-level inverter

设L1=L2=L3=L4=L、C1=C2=C，由于阻抗网络结构对称，从而有uL1=uL2=uL3=uL4=uL，uC1=uC2=uC。电压的提升是通过三电平逆变桥的桥臂直通实现的，即在常规电压矢量之间插入直通矢量。SL型Z源三电平逆变器采用半直通状态和非直通状态切换的方式实现升压和电压输出，半直通又包括上直通和下直通2种状态。如a相半直通的等效电路如图2所示，具体原理可参考文献[9]。设电容CS1和CS2的电压均为udc/2，直流链电压的高低电平峰值分别为uinH和uinL，则上直通和下直通时均有uL=udc/2、uinL=uC-uL。

非直通状态的等效电路如图3所示。此时有2uL+uC=udc、uinH=uC-2uL。

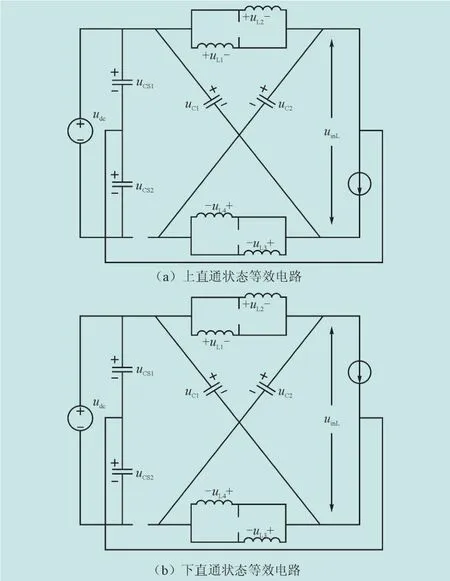
图2 SL型Z源三电平逆变器半直通状态等效电路Fig.2 Equivalent circuits of the switched-inductor Z-source three-level inverter of upper and lower shoot-through states

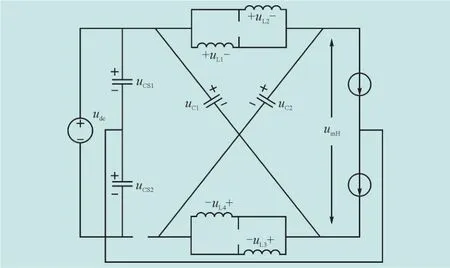
图3 SL型Z源三电平逆变器非直通状态等效电路Fig.3 Equivalent circuit of the switched-inductor Z-source three-level inverter of non-shoot-through state

设一个开关周期Ts内，上直通时间为tUS，下直通时间为tDS。为了使Z源网络输出电压在2种直通状态下相等，应满足tUS=tDS=tS。利用稳态时一个开关周期内电感电压的伏秒数为0，推出Z源阻抗网络电容电压为

直流链电压高电平峰值为

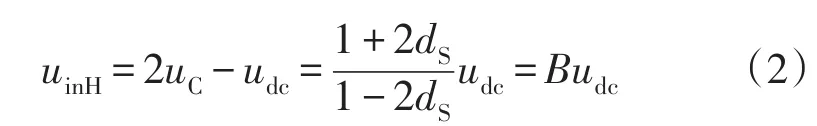
式中：B为升压因子，B=(1+2dS)/(1-2dS)；dS为直通占空比，dS=tS/Ts。由于B＞1，因此引入SL型Z源阻抗网络后实现了直流侧电压的提升。

2 直流侧模型

设Z源网络4个电感的等效串联电阻均为rL；2个电容的等效串联电阻均为rC；上部开关电感中2个电感的电流均为iL1；下部开关电感中2个电感的电流均为iL2；中性线上方的负载电流为iload1；下方的负载电流为iload2。

定义状态变量x=[iL1iL2uC1uC2]T、u=[udciload1iload2]T。上直通时状态方程为

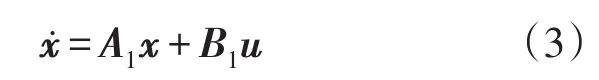
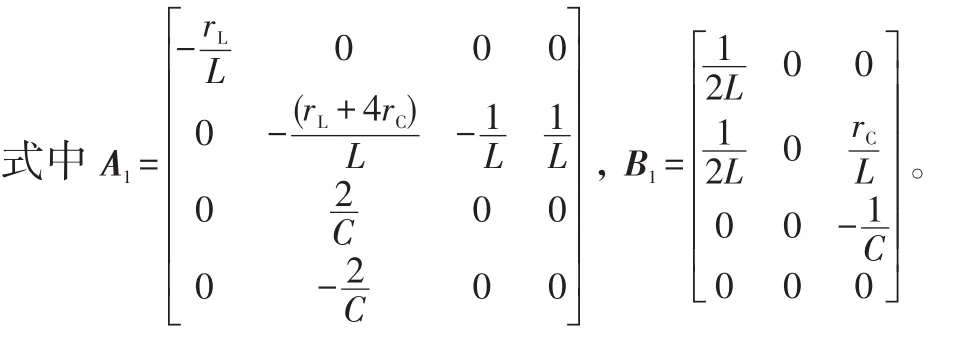
下直通时状态方程为

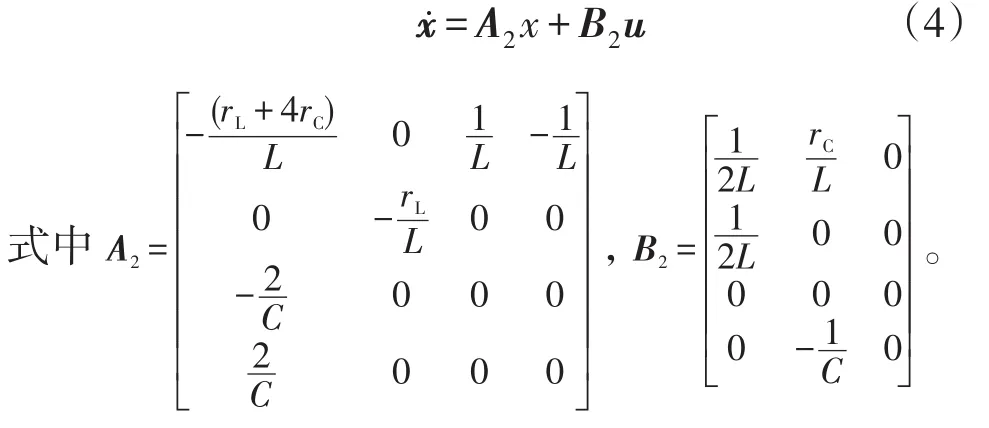
非直通时有

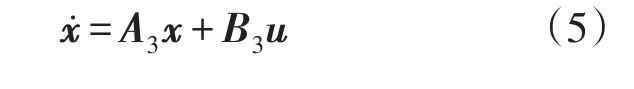
用状态空间平均法对SL型Z源阻抗网络进行建模，其平均模型为

式中

其中dS为上直通和下直通的动态占空比。

系统的直流状态方程，即静态工作点为

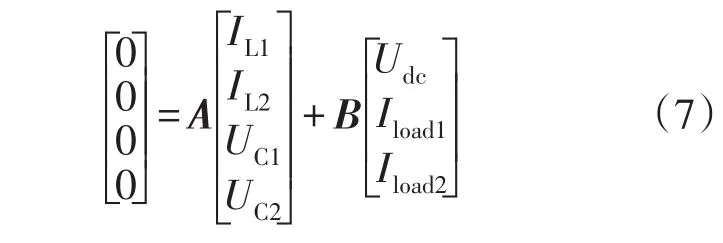
式中：IL1=IL2=IL为Z源网络电感电流的静态工作值；UC1=UC2=UC为Z源网络电容电压的静态工作值；Iload1=Iload2=Iload为负载电流的静态工作值。而A=DSA1+DSA2+（1-2DS）A3，B=DSB1+DSB2+（1-2DS）B3，其中DS为上直通和下直通的静态占空比。

对直流状态方程进行小信号扰动，从而得到小信号模型。令X=[ILILUCUC]T、U=[UdcIloadIload]T。将包含扰动量的状态变量代入式（6），得小信号动态方程为

对式（8）进行拉氏变换，并求出x（s）为

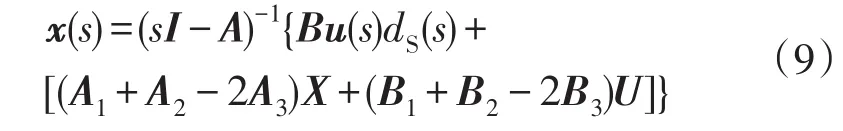
由于Z源网络的对称性，式（9）中的矩阵A、A1、A2、A3、B、B1、B2、B3可简化为2×2矩阵，向量x（s）、u（s）、X、U、dS（s）简化为2×1向量，于是有

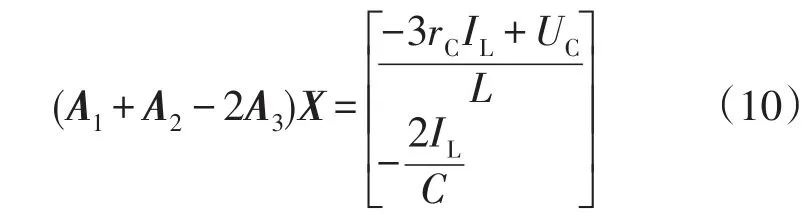
推导出基于开关电感的Z源网络电容电压表达式为

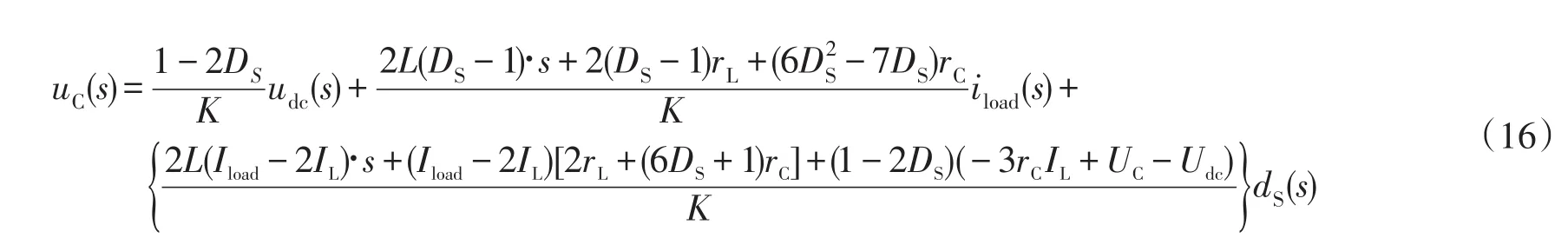
令上式中udc（s）=0、iload（s）=0，得直通占空比dS（s）至Z源网络电容电压uC（s）的传递函数：

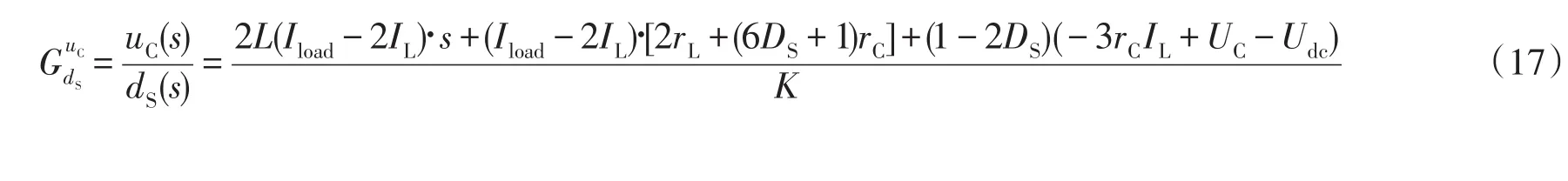
静态工作点运行时，将式A、B以及X=[ILUC]T

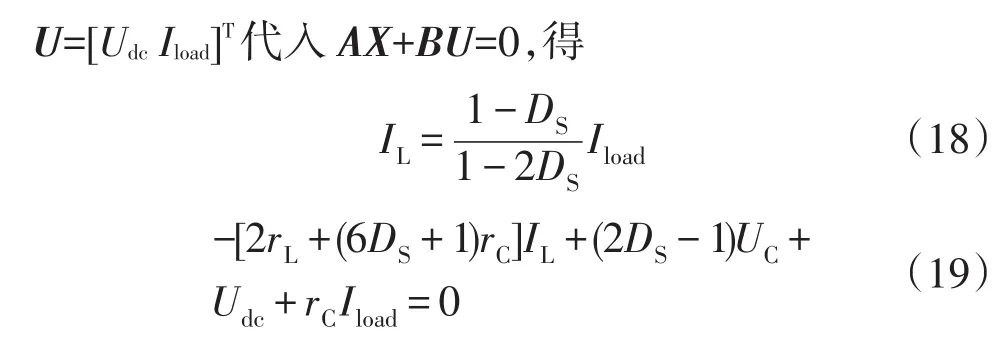
从而有IL＞Iload，由式（17）可知，有一个右半平面零点，具有非最小相位特性，这一点与常规Z源网络相同。

设定表1所示的参数为额定条件下的参数，分析额定条件下的零极点分布情况。

由式（18）算得IL=13.33 A，再由式（19）算得UC= 329.50 V，则式（17）传递函数的参数都为已知。作出随Z源网络电容和电感变化时的零极点分布图，分别如图4（a）和图4（b）所示。传递函数有1个零点，此零点不随电容参数变化，但随着电感的增加越来越靠近虚轴，非最小相位现象越来越严重。当电容和电感逐渐增加时，极点均越来越靠近实轴。

表1 额定条件参数Table 1 Nominal parameters

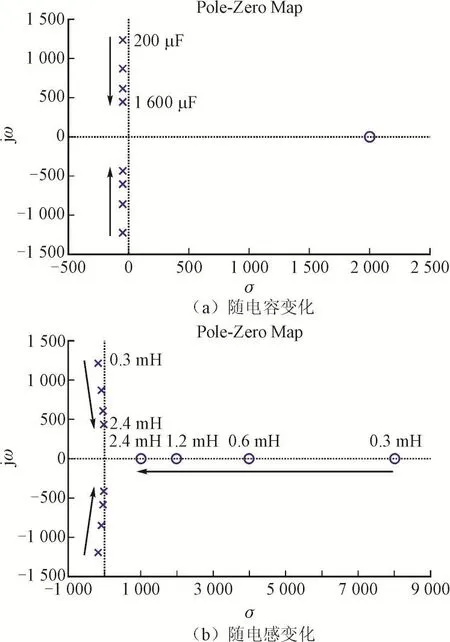
图4 的零极点随Z源网络参数变化时的轨迹图Fig.4 Pole-zero loci ofwith the change of Z-source network parameters

由分析可知，SL型Z源三电平逆变器直通占空比至Z源网络电容电压的传递函数特性与常规Z源两电平逆变器的相似；同理，直通占空比至直流链电压高电平峰值传递函数的特性也与常规Z源两电平逆变器的相似。

3 直流链电压滑模控制器设计

3.1 控制率推导

直流链电压为高频脉动电压，不易检测和控制。由于直流链电压高电平峰值uinH与Z源网络电容电压uC有对应关系，因此本文通过控制uC间接地控制uinH。由于Z源网络的对称性，选择其中1个电容的电压和其中1个电感的电流作为反馈量。选取Z源网络的状态变量为

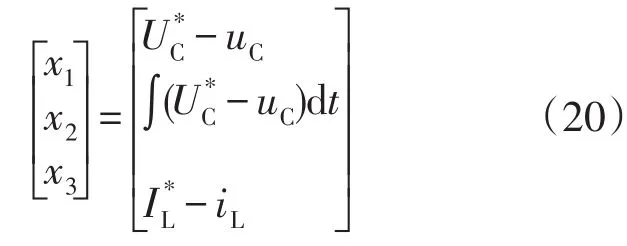
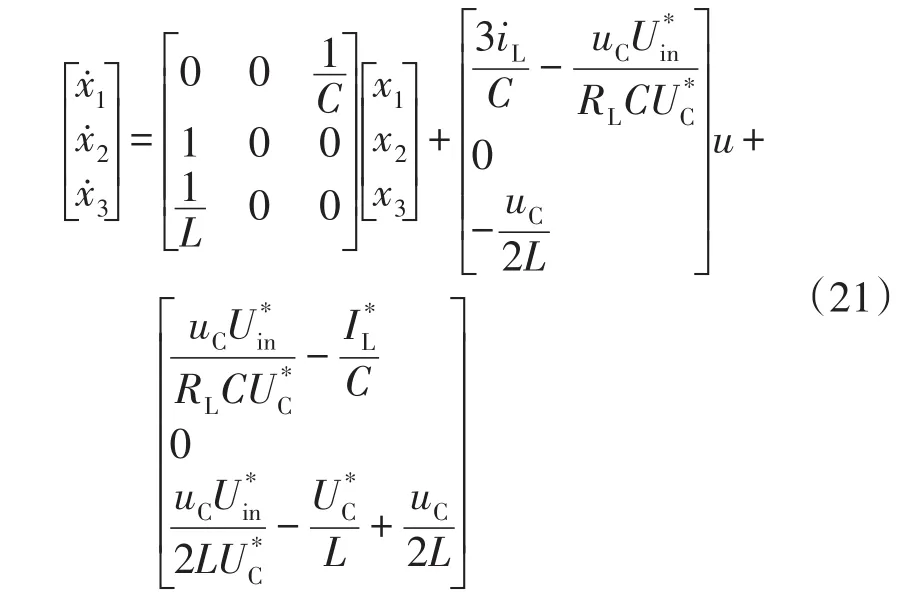
式（21）可表示为标准形式：

选定滑模面为

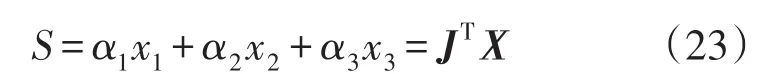
式中J=[α1α2α3]T，为滑模系数向量。令S=0，推导出等效控制律为

3.2 存在性和稳定性条件

滑模控制器的控制作用为

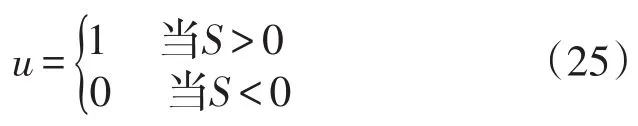
存在性条件可通过满足局部可达性条件来满足，即

式（26）还可以表示为

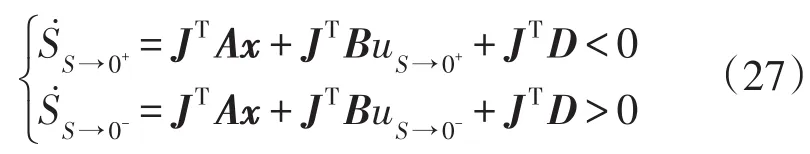
式（27）分为2种情况：

情况1：S→0+，＜0

用u=1替换uS→0+，将A、B、D代入式（27）的第1式，得

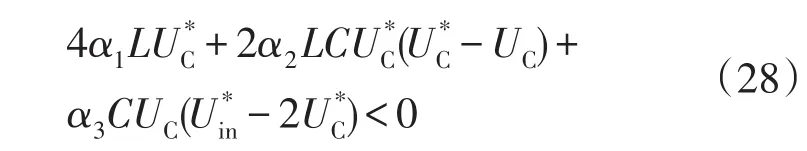
情况2：S→0-，＞0

用u=0替换uS→0-，将A、B、D代入式（27）的第2式，得

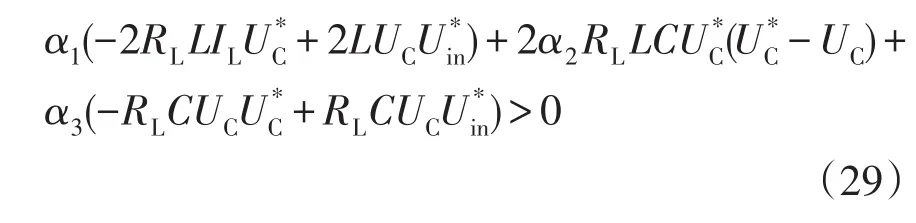
滑模控制器的稳定性分析可参考文献[22]。所选择的滑模系数应同时满足式（28）、式（29）和稳定性条件。

4 仿真研究

建立了SL型Z源三电平逆变器的仿真模型，控制器和脉冲宽度调制采用了Matlab的s函数编写，s函数语句与DSP的C语言较为接近，便于以后样机实验的程序编写。仿真参数：直流电源电压udc=200 V，本文不研究中点电位平衡问题，因此将直流侧分压电容用2个直流电源代替，电源电压均为udc的一半，即100 V；Z源网络电感L=1.2 mH，C=2 200 μF；逆变器输出滤波电感Lf为3 mH，滤波电容Cf为5 μF；负载为三相电阻，阻值RL为200 Ω；开关频率fS为10 kHz，三相输出电压频率f为50 Hz；滑模系数α1=6、α2=900、α3=100；直流链电压参考值设定为1 600 V，根据式（1）和式（2）可计算出与之对应的电容电压参考值为900 V。

首先研究直流链电压的开环控制，根据式（2）计算出使直流链电压高电平峰值为1 600 V时的dS为0.388 9，并在仿真中直接将dS设为该值。图5为开环控制时直流链电压稳态波形，非直通时高电平峰值电压为1 585 V，上直通和下直通时低电平峰值电压为792 V，高电平峰值偏离1 600 V较多。可见必须对直流链电压采取闭环控制方式。

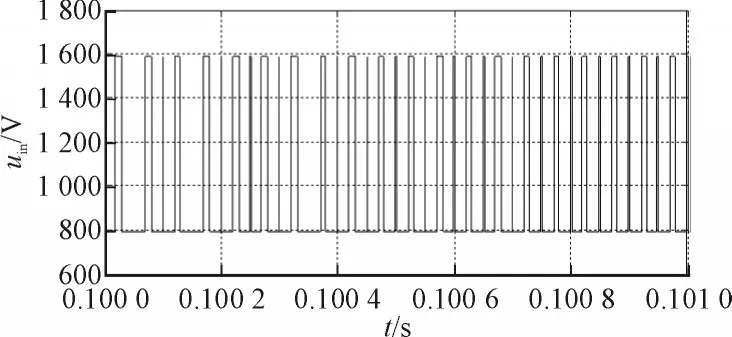
图5 开环控制时直流链电压稳态波形Fig.5 Static waveform of the dc-link voltage with the open-loop control

图6为采用滑模控制时直流链电压的稳态波形，可以看出，直流链电压为高频脉动电压，非直通时高电平峰值电压为1 600 V，上直通和下直通时低电平峰值电压为800 V，高电平峰值跟踪参考值，稳态误差非常小。

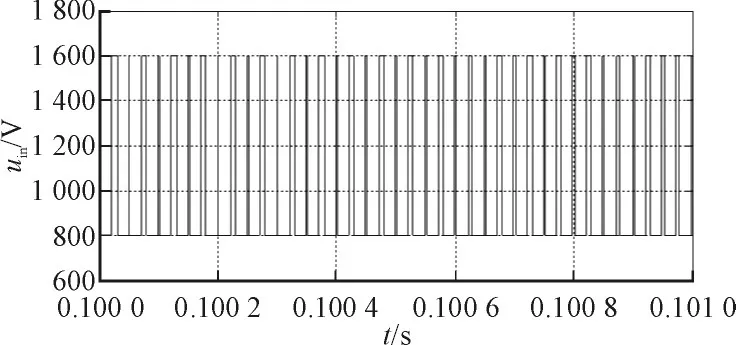
图6 滑模控制时直流链电压稳态波形Fig.6 Static waveform of the dc-link voltage with the sliding mode control

图7为其中1个电感的电流波形，其余3个电感电流波形与其大致相同。由图7可见，稳态时电感电流的平均值大约为10 A，并且含有一定的纹波，这是因为在半直通和非直通的状态转换过程中，电感电压高频变化，使电流频繁升降。

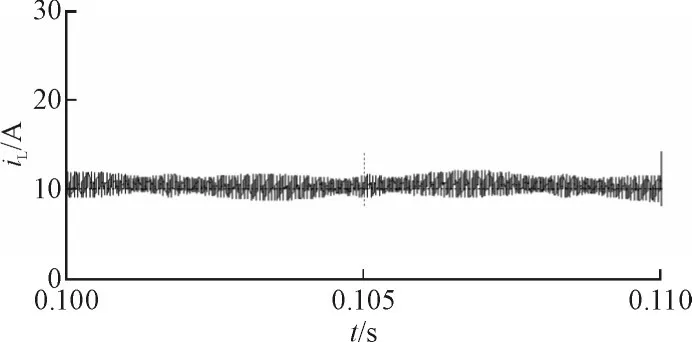
图7 滑模控制时电感电流稳态波形Fig.7 Static waveform of the inductor current with the sliding mode control

图8为Z源阻抗网络电容电压uC的稳态波形，仿真开始后，电容电压从0 V开始上升，经历启动的暂态过程并稳定于约900 V，稳态误差也非常小。

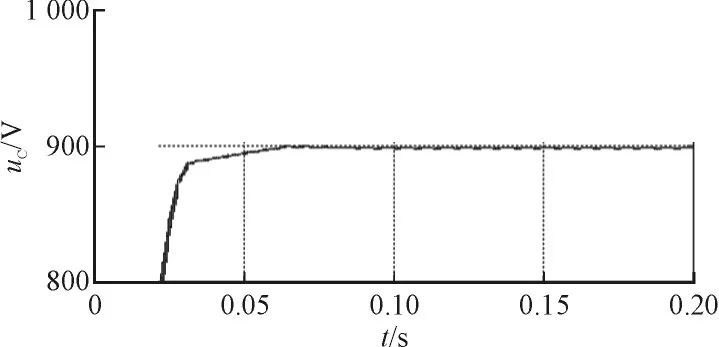
图8 滑模控制时Z源阻抗网络电容电压稳态波形Fig.8 Static waveform of the Z-source impedance network capacitor with the sliding mode control

图9为Z源三电平逆变器输出的三相交流电压，仿真中设定三相交流参考电压的峰值为560 V，实际输出电压的峰值非常接近560 V，可见对直流链电压的进行控制能够使输出交流电压的电压质量得到保证。

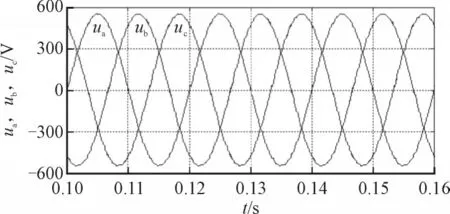
图9 滑模控制时逆变器输出电压稳态波形Fig.9 Static waveforms of inverter output voltages with the sliding mode control

图10为直流链电压的暂态波形，仿真中设定t=0.14 s时udc由200 V突变为220 V。由波形可见，直流链电压高低电平峰值在0.14 s时出现小幅下降，然后逐渐恢复至约1 600 V和800 V，暂态过程不是非常剧烈。

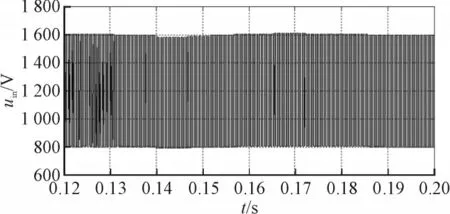
图10 滑模控制时直流链电压暂态波形Fig.10 Transient waveform of dc-link voltage with the sliding mode control

5 结论

开关电感型Z源三电平逆变器的直流侧表现出非线性特性，直通占空比至Z源阻抗网络电容电压的传递函数具有非最小相位特性，适合采用非线性控制策略控制直流链电压。本文设计的直流链电压滑模控制器通过控制Z源阻抗网络电容电压间接地控制直流链电压的高电平值，推导出的滑模控制器形式简单，容易实现，且满足存在性和稳定性条件。仿真结果证明所设计的控制器使开关电感型Z源三电平逆变器的直流侧电压具有良好的动态和暂态性能。

[1]龚博，程善美，秦忆.基于载波的三电平中点电压平衡控制策略[J].电工技术学报，2013，28（6）：172-177. GONG Bo，CHENG Shanmei，QIN Yi.A three-level neutral point voltage balance control strategy based on carriers of SPWM[J].Transactions of China Electrotechnical Society，2013，28（6）：172-177.

[2]XIAO H F，XIE S J.Transformerless split-capacitor neutral point clamped three-level PV grid-connected inverter[J]. IEEE Trans on Power Electr，2011，27（4）：1799-1808.

[3]王峰，张旭隆，何凤有，等.基于复合模型预测控制的三电平APF研究[J].电力系统保护与控制，2014，42（11）：79-85. WANG Feng，ZHANG Xulong，HE Fengyou，et al. Research of three-level shunt APF control method based on composite model predictive control strategy[J].Power System Protection and Control，2014，42（11）：79-85.

[4]RAMKRISHAN M，STIG M N，SERGIO B M.Design of neutral-point voltage controller of a three-level NPC inverter with small DC-link capacitors[J].IEEE Transactions on Industrial Electronics，2013，60（5）：1861-1871.

[5]PENG F Z.Z-source inverter[J].IEEE Transactions on Industry Applications，2003，39（2）：504-510.

[6]FRANCIS B E，PATRICK W，JON C，et al.Space-vectormodulated three-level inverters with a single Z-source network[J].IEEE Transactions on Power Electronics，2012，28（6）：2806-2815.

[7]LOH P C，GAO F，BLAABJERG F，et al.Pulsewidthmodulated Z-source neutral-point-clamped inverter[J]. IEEE Transactions on Industry Applications，2007，43（5）：1295-1308.

[8] 贺昱曜，冯伟，宋石磊.Z源级联三电平中点钳位逆变器[J].电网技术，2012，36（4）：219-223. HE Yuyao，FENG Wei，SONG Shilei.A cascaded Z-source three-level neutral point clamped inverter[J].Power System Technology，2012，36（4）：219-223.

[9] 王晓刚，张杰.基于开关电感的增强型Z源三电平逆变器[J].电力系统保护与控制，2015，43（16）：65-72. WANG Xiaogang，ZHANG Jie.Enhanced Z-source threelevel inverter based on switched-inductor[J].Power System Protection and Control，2015，43（16）：65-72.

[10]张瑾，齐铂金，张少如.Z源三电平中点钳位逆变器的空间矢量调制方法[J].电工技术学报，2010，25（9）：108-114，144. ZHANG Jin，QI Bojin，ZHANG Shaoru.A space vector PWM algorithm for Z-source three-level NPC inverters[J]. Transactions of China Electrotechnical Society，2010，25（9）：108-114，144.

[11]LOH P C，GAO F，BLAABJERG F，et al.Operational analysis and modulation control of three-level Z-source inverters with enhanced output waveform quality[J].IEEE Transactions on Power Electronics，2009，24（7）：1767-1775.

[12]KUMAR S S，JYOTHI B，DEEPIKA K K.Three level Z source inverter using space vector PWM[C]//2015 International Conference on Electrical，Electronics，Signals，Communication and Optimization，Visakhapatnam，India，2015.

[13]张瑾，齐铂金.Z源三电平中点钳位逆变器中点电位平衡控制方法[J].中国电机工程学报，2010，30（12）：7-13. ZHANG Jin，QI Bojin.Neutral-point potential balancing method for Z-Source three-level NPC inverters[J].Proceedings of the CSEE，2010，30（12）：7-13.

[14]SHI X，CHEN A，ZHANG C.A neutral-point potential balancing method for Z-source neutral-point-clamped（NPC）inverters by adding the shoot-through offset[C]// 2014 International Power Electronics and Application Conference and Exposition，Shanghai，China，2014.

[15]张伦健，谭国俊，陈利萍.基于双调制波技术的三电平Z源逆变器中点电位平衡控制[J].电力系统保护与控制，2013，41（7）：91-96. ZHANG Lunjian，TAN Guojun，CHEN Liping.Neutralpoint potential balance control for three-level Z-source inverters based on double modulation wave technique[J]. Power System Protection and Control，2013，41（7）：91-96.

[16]MARTIN S，STEFFEN B，JULIAN W，et al.Adaptive closed-loop state control system for a three-level neutralpoint-clamped Z-sourceinverter[J].IET Electrical Systems in Transportation，2016，6（1）：12-19.

[17]HU J B，SHANG L，HE Y K，et al.Direct active and reactive power regulation of grid-connected DC/AC converters using sliding mode control approach[J].IEEE Transaction on Power Electronics，2011，26（1）：210-222.

[18]陈宗祥，蒋赢，潘俊民，等.基于滑模控制的Z源逆变器在单相光伏系统中的应用[J].中国电机工程学报，2008，28（21）：33-39. CHEN Zongxiang，JIANG Ying，PAN Junmin，et al.A Z-source inverter for a single-phase PV system based on sliding-mode control[J].Proceedings of the CSEE，2008，28（21）：33-39.

[19]SATISH K G，RAJESH G.Recursive fast terminal sliding mode control in voltage source inverter for a low-voltage microgrid system[J].IET Generation，Transmission& Distribution，2016，10（7）：1536-1543.

[20]KANG S W，KIM K H.Sliding mode harmonic compensation strategy for power quality improvement of a grid-connected inverter under distorted grid condition[J].IET Power Electronics，2015，8（8）：1461-1472.

[21]MILAN C，KAREL J，ROBERT H.FPGA-Based predictive sliding mode controller of a three-phase inverter[J]. IEEE Transactions on Industrial Electronics，2013，60（2）：637-644.

[22]王晓刚，肖立业.Z源逆变器直流链电压滑模控制研究

[J].电机与控制学报，2015，19（2）：1-6.

WANG Xiaogang，XIAO Liye.Sliding mode control for DC-link voltage of Z-source inverter[J].Electric Machines and Control，2015，19（2）：1-6.