海底管道后挖沟过程的应力解析分析方法

， ， ，经天

(1.中国石油大学(北京)机械与储运工程学院 北京 102249; 2.中石化天津液化天然气有限责任公司 天津 300457)

·试验研究·

海底管道后挖沟过程的应力解析分析方法

夏梦莹1，张宏1，吴锴1，吴经天2

(1.中国石油大学(北京)机械与储运工程学院 北京 102249; 2.中石化天津液化天然气有限责任公司 天津 300457)

海底管道在后挖沟过程中会产生较大的变形，此时管道内产生较大的应力，对管道安全的运行形成威胁。因此准确给出挖沟过程中管道应力计算方法具有重要意义。基于弹性梁理论，给出了挖沟过程中管道挠曲线微分方程，通过边界条件与协调方程，给出了考虑几何非线性的挖沟过程中管道应力与变形解析计算方法。通过与有限元数值模型对比得到本解析方法结果与数值方法结果基本一致，可以用于工程中海底管道的应力计算。

海底管道；挖沟敷设；应力；解析方法；数值验证

0 引 言

海底管道在海洋油气开发过程中担任着重要的作用。管道的挖沟埋设，是指用水下挖沟机械在海床上挖出一条指定深度、指定形状的沟槽，并将海底管道埋藏在沟槽之中，以达到保护管道的目的[1]。这种敷设在我国近海得到了广泛的应用，挖沟敷设后的管道能够更好的避免抛锚等第三方事故对管道的影响[2]。

由于海底管道挖沟过程中管道内会产生较大的变形与应力，从而保证管道在挖沟过程中的强度安全有着重要的实际意义。然而针对这方面的研究较少[3,4]。帅健[5]提出了一种管道挖沟状态下应力解析分析方法，但是其没有考虑轴向变形对管道应力的影响。刘秉德[6]基于AutoPIPE软件开展了X60管道的挖沟过程的数值模拟分析，给出了最大弯曲应力与变形的变化趋势，然而其结果的适用性有限。总而言之，现有的研究对工程实际的应用范围有限。因此，本文给出一种通用的海底管道在挖沟过程中应力分析的解析方法。方法基于弹性梁理论确定管道的弯曲变形，基于伸长量协调条件考虑轴向应力的影响。基于本方法能够准确的得到海底管道挖沟过程中的应力与变形结果。

1 管道力学模型

挖沟条件下管道变形形状如图1所示，沟深为Δ，管子在海水中的单位长度重量为q，AB段为上部悬空段，设其长度为l1；BC段为下部悬空段，设其长度为l2。假设基础是刚性的，从而可以得到躺在刚性基础上的部分管道存在弯矩为零的边界条件。

最终可以得到弯曲段的受力如图所示，在A、B、C点分别作用有三个集中力RA、RB和RC，这三个集中力和图中的悬空长度l1和l2均为未知量。

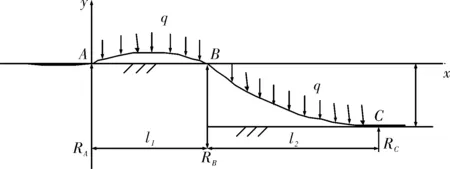
图1 挖沟条件下管道变形示意图

1.1 弯曲变形分析

以A点为坐标原点，建立坐标系，对于AB段，弯曲微分方程为

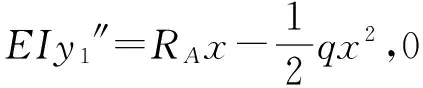
(1)

代入段的边界条件y1″|x=0=0,y1′|x=0=0,y1|x=0=0,y1|x=l1=0

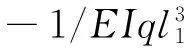
对于BC段，弯曲微分方程为

EIy2″=RAx+RB(x-l1)-1/2qx2,l1≤x≤l1+l2

(2)

在B点处转角连续，可以得得到：C3=0。

BC段边界条件为：y2|x=l1=0,y2|x=l1+l2=-Δ,y2′|x=l1+l2=0,y2″|x=l1+l2=0

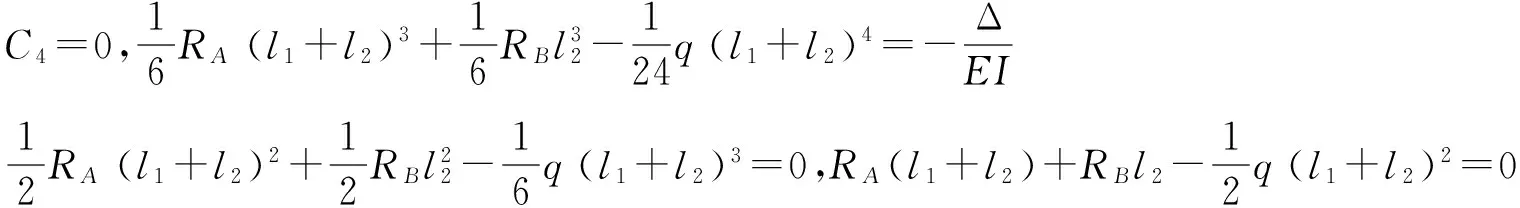
从而可以得到

RB=1/2l2q(l1+l2)(1/2l1+l2)

(3)

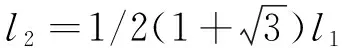
从而可以得到：l1=1.96(ΔEI/q)1/4

各段弯矩

(4)

从而可以得到最大弯矩作用在B处，其大小为

(5)

从而可以得到，最大弯矩随管道的单位长度的水下重量、抗弯刚度和沟深的增大而增大。

同时根据对B点求矩的平衡可以得到：

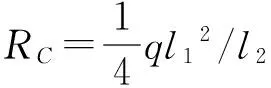
1.2 管道轴向变形

1.2.1 几何伸长量

管道的几何伸长量主要来自于管道变形后曲线长度的增加，可以通过弧长积分法得到变形后的曲线长度，从而得到管道的几何伸长量

(6)

1.2.2 物理伸长量

管道的物理伸长量由轴向变形积分得到，轴向变形主要由四段管道的变形产生，A点左侧管道，AB段管道，BC段管道，C点右侧段管道。其中AB段与BC段管道内轴向力在B点处于B点处集中力形成一个平衡，受力关系如图2所示。

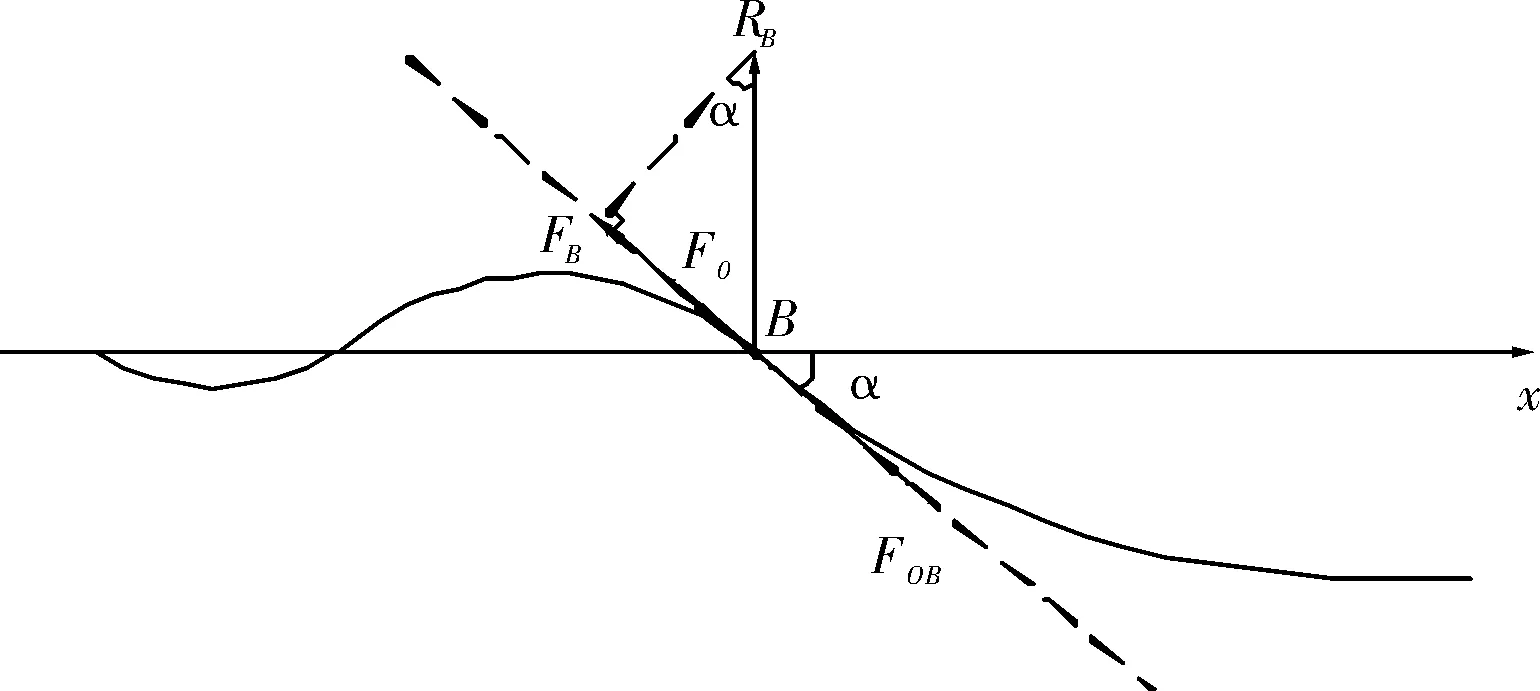
图2 B点受力平衡示意图

首先假设AB段轴力大小为F0，从而可以得到B点管道轴向分量为：FB=RBsin(α)=RBsin(atan(yB′))，因此BC段轴力FOB=F0+FB。

管道物理伸长量计算方法如式(7)：

(7)

根据两者协调条件可以得到管道的轴向力大小F0，由于管道受拉所以舍弃负值，从而可以得到：

F0=

1.3 管道轴向应力

管道内的轴向应力包括，轴力引起的应力分量σ0=F0/A；温度与内压引起的管道的轴向应力σserive=-Eα(T2-T1)+vσh；弯矩引起的轴向应力σbend=MR/I。三者求和可以得到管道的轴向应力的总大小：σaxial=σservice+σbend+σ0。

2 模型准确性验证

为了验证本文方法的准确性，这里采用实际工程参数进行计算，并将计算结果与有限元模型结果进行对比。工况参数如下：管径500 mm，壁厚6 mm，摩擦系数0.5，热胀系数1.2e-5，单位长度管道重量720 N/m，管沟深度1 m。

有限元模型使用ABAQUS软件建立，使用PIPE21单元模拟管道，使用离散刚体模拟海床，使用通用接触定义两者接触关系，所有参数与采用上面给出的工况参数，计算分为两个载荷步，第一个载荷步为工作荷载施加载荷步，第二个载荷步为管沟冲沟载荷步。在第一个载荷步施加内压，温度等载荷，第二个载荷步中将右侧土块下移模拟冲沟产生的沟底深度。计算结果如图3所示。

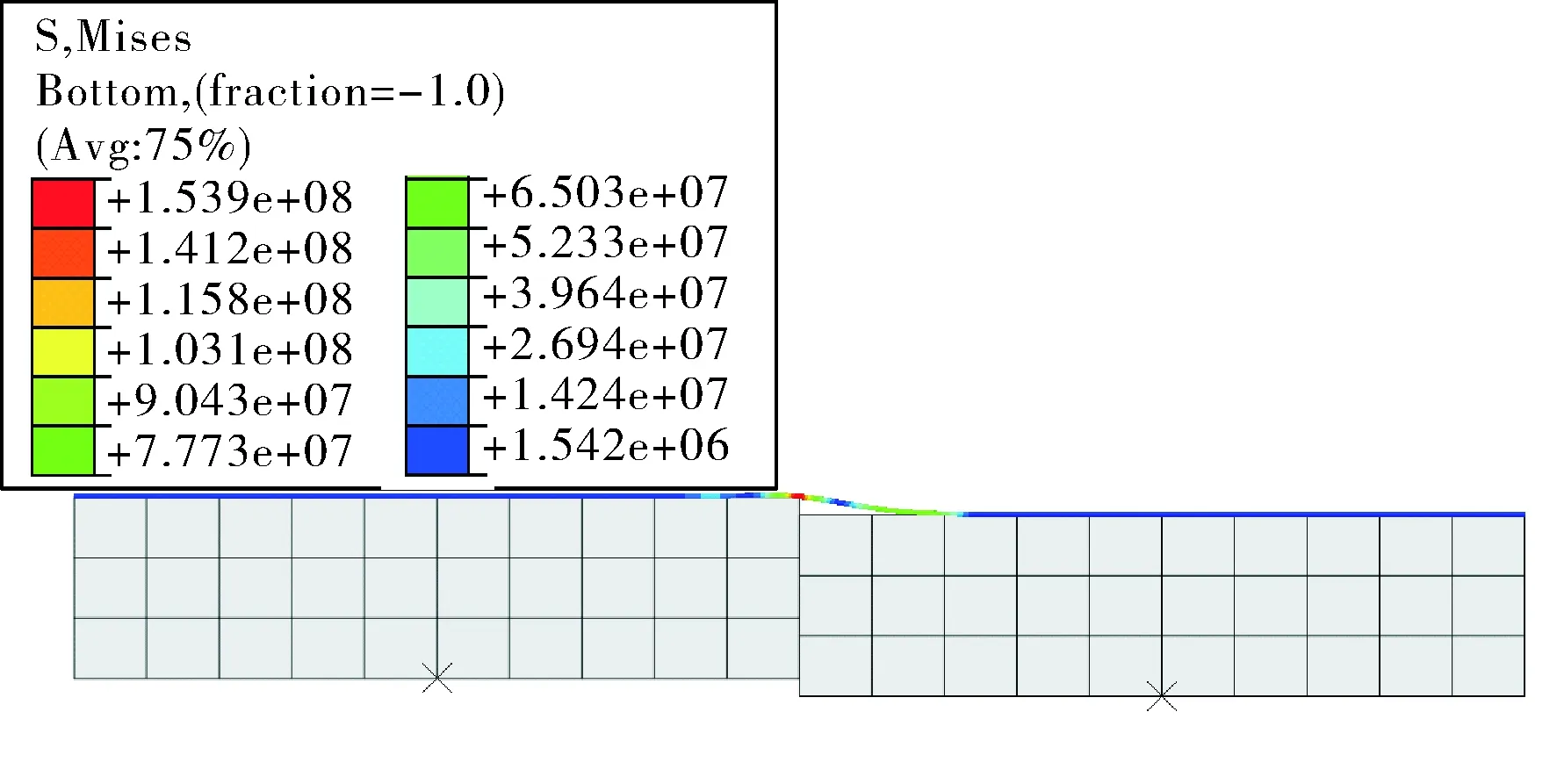
图3 挖沟条件下管道响应数值计算模型

图4给出了本文解析结果与有限元结果的对比图。结果表明，管道在B点处应力最大，B点管顶轴向应力为轴向拉应力，管底为轴向压应力。本文方法与数值计算方法吻合很好，从工程角度，两者误差几乎可以忽略。从而表明了本文给出方法的准确性和合理性。

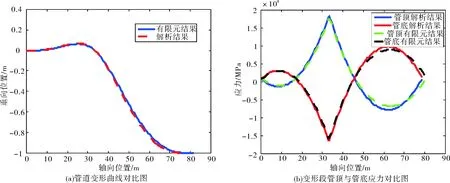
图4 变形段位移与应力结果

3 结 论

本文基于弹性梁理论给出了一种海底管道挖沟过程中应力与变形求解的解析分析方法，方法基于弹性梁理论，得到了管道的挠曲线微分方程，基于边界条件得到了挠曲线方程的解析解，并由此得到了管道内弯曲应力。在此基础上，通过管道几何伸长量和物理伸长量的协调条件，得到了管道内的轴向力应力。最终通过弯曲应力与轴向应力叠加得到管道内的轴向总应力。通过与有限元数值模型对比得到本解析方法结果与数值方法结果基本一致，可以给工程实际提供一定的参考。

[1] 方维章. 国外海底管线的铺设和开沟埋管技术[J]. 海洋工程, 1983(3):82-88.

[2] 孟 然. 海底管道后挖沟技术实验研究及数值模拟[D]. 天津大学, 2012.

[3] PAULIN M，HUMBY D，COCKER J，et al． Trenching of Pipelines for Protection in Ice Environments [C]. SPE Arctic and Extreme Environments Conference and Exhibition, SPE, 2011: 1-7.

[4] 秦卫华. 海底管道挖沟技术的改进[J]. 江苏船舶, 2010, 27(1):18-20.

[5] 帅 健. 海底管线开沟埋设时的应力分析[J]. 石油机械, 1997(8):39-40.

[6] 刘秉德, 倪玲英, 詹燕民,等. 海底管道挖沟的数值模拟[J]. 管道技术与设备, 2014(6):5-7.

AnalyticalStressAnalysisMethodforSubmarinePipelineduringTrenching

XIAMengying1,ZHANGHong1,WUKai1,WUJingtian2

(1.CollegeofMechanicalandTransportationEngineering,ChinaUniversityofPetroleum-Beijing,Beijing102249,China; 2.SINOPECTianjinLiquefiedNaturalGasCo.Ltd.,Tianjin, 300457,China)

During the after trenching process, large deformation will occur in the pipe, which can induce large stress leading to the potential failure. Thus an accurate stress estimation method for pipelines under this load condition was necessary. Based on elastic beam theory, the pipe deflection equations were proposed. The analytical stress and deformation results were derived by the boundary conditions and the coordination condition between the geometrical elongation and the physical one. Finally, this proposed method was validated accuracy for calculating pipe stress by comparing with a finite element model.

submarine pipeline； trenching lay； stress； analytical method； numerical validation

夏梦莹，女，1990年生，在读博士研究生，主要从事油气装备失效分析与安全评价。E-mail：xiamengying322@163.com

TE 973

A

2096-0077(2017)06-0041-03

10.19459/j.cnki.61-1500/te.2017.06.011

2017-04-20

马小芳)