大学生就业偏好群体划分方法

韩雪峰 刘 洋

（辽宁工程技术大学 辽宁 阜新 123000）

引言

随着大学生数量的不断增多和就业形势的复杂多样，对大学生的就业偏好及其影响因素进行分析是当前高等教育研究领域的一个重要课题[1][2]。现有大多数分析方法通常以调研的整个学生群体作为分析对象，很少或没有综合考虑按家庭条件、学习成绩、兴趣爱好、性别等对学生群体进行划分，因而导致分析结果不具有针对性和精准性[3][4]。而在现实应用中，大学生的就业意愿及其影响因素在很大程度上与其背景信息（如家庭条件、学习成绩、生源地、兴趣爱好、父母学历、性别等）密切相关，因此需要先对大学生的背景信息进行详细调查，进而将学生群体进行划分，从而精准分析每类学生的就业意愿及其影响因素。近年来，有一些研究工作开展了针对不同类别大学生的就业价值取向的问题研究，如文献[5]根据大学生生源地的不同，提出了西部少数民族大学生在就业过程中面临的问题和价值取向；文献[6]针对农村大学生的“就业难”问题展开了深入分析和研究，并提出了相应的解决对策；文献[7]从性别角度，研究了女大学生就业质量和影响因素评价体系。上述研究虽然对大学生群体进行了划分，但划分标准都基于单因素（如仅从生源地、农村城市、性别等方面），并没有综合考虑学生背景信息多因素之间的复杂耦合关系。本文从学生背景信息出发，根据学生在背景信息多因素（如综合考虑父母职业、学历、家庭收入、学习成绩、性别等）方面的耦合相似度，提出典型大学生选取和学生群体划分方法，使得同类学生群体内部学生之间具有较高的综合相似/相关度。

本文组织结构为：第一部分阐述大学生背景信息之间的耦合关系分析方法；第二部分提出学生典型程度度量方法；第三部分提出top-k典型学生近似选取方法以及学生群体划分方法；第四部分是实验结果分析与性能评价。

一、大学生背景信息之间的耦合关系分析

本文所述的耦合关系是指学生背景信息之间存在的各类显式或隐含关联关系。给定两个学生，如果他们在背景信息的各个维度上都很相似或相关，则这两个学生之间就具有较强耦合关系，通常应该被划分到相同群体。例如，在家庭住址方面，两个学生居住在相同或相近的区域；在学习成绩方面，两个学生的专业必修课成绩接近；在兴趣爱好方面，两个学生都偏好统计分析和软件编程等。反之，如果他们在背景信息上的关联度较小，则他们之间的耦合关系较弱。例如，生活在农村的大学生和生活在一线城市的大学生，他们在家庭条件、父母职业、兴趣爱好方面可能都有很大不同，进而导致就业意向和择业时考虑因素上的差别。而这些学生，应该被划分到不同群体，分别归属于不同类别。

表1 学生背景信息实例

（一）学生背景信息向量空间模型的构建

本文主要从以下方面调研学生的背景信息，包括父母职业、父母受教育程度、父母政治面貌、家庭收入、家庭所在地、所学专业、平均成绩、性别等10个属性，其中父母职业、父母教育程度、父母政治面貌、家庭所在地、所学专业及性别是文本属性，家庭年收入、平均成绩是数值属性。表1给出了学生背景信息的数据实例。

从上表可以看出，每个学生的背景信息都可由{父亲职业、母亲职业、父母教育程度、父亲政治面貌、母亲政治面貌、家庭收入、家庭所在地、所学专业、平均成绩、性别}属性上对应的值来描述。例如，表1中序号为1的学生，其父亲职业为“国家机关、党群组织、企业、事业单位”，母亲职业是“专业技术人员”，父母教育程度为“大学及以上”，父亲政治面貌是“群众”，母亲的政治面貌是“群众”，家庭年均总收入为“十万位”，家庭所在地为“县/乡镇”，所学专业是“农学”，本科时专业课平均成绩为“70”，性别是“男”。

表2 “学生1”背景信息对应的向量表

下面讨论如何根据学生的背景信息评估任意一对学生之间的耦合关系。来看一个例子，在表1中，序号为1和2的学生父母职业分别是“国家机关、党群组织、企业、事业单位”和“专业技术人员”，如果按照传统的严格关系匹配方法，也就是所有属性上的取值必须完全相同，则学生1和学生2之间的相似度为0；但实际上，即便是这两个学生描述信息之间不完全匹配，也就是说仅在部分属性上相匹配，他们之间也有可能是相似的。在上例中，学生1和学生2的父母政治面貌都是“群众”，家庭收入都是“十万位”，性别都是“男”，因此他们之间具有一定的相似性。本文目的在于利用这种在部分属性上的相似/相关关系来精确量化两个学生之间的耦合相似度，基本思想是根据背景信息构建每个学生的向量空间模型，然后通过评估背景信息向量表之间的重合程度来计算不同学生之间的耦合相似度。

背景信息的向量表可用一个两栏结构表示，由属性（Attributes）和值信息（Values）两列构成，表2和表3分别给出了大学生背景信息数据集上对于“学生1”和“学生2”的向量表，向量表中的每个属性对应向量中的一个分量。

表3 “学生2”背景信息对应的向量表

（二）耦合相似度评估方法

根据上文所述，学生背景信息向量表中包含了对应于每个属性的值，所以可根据向量表中各个属性上值的相似度来计算学生之间的耦合关系度。

由于本文调研的学生背景信息仅包含文本和数值两类属性，文本值之间的相似度容易处理，主要根据两个值是否重合，重合即为1，否则为0。如果一个属性下有多个值，则利用Jaccard系数进行计算相似度，即 J（A，B）其中A、B分别代表两个向量表中相同属性上对应的值集合，例如表2和3中的属性“母亲职业”，A={国家机关，专业技术}，B={工厂，专业技术}，则它们在该属性上的Jaccard系数为1/3。

由于数值之间具有连续性，我们不能直接利用上述方法量化数值之间的相似度，例如两个学生的专业课平均成绩分别是70和72，这两个值在数值上接近，不能完全看成是两个不同的值，本文借鉴模糊集理论的基本方法评估数值之间的语义相似度。根据模糊集理论，给定一个数值Y，在数值上接近Y的数构成了一个模糊集合，用“close to Y”表示，它的隶属函数在论域U上定义为

其中，u为论域U上的一个元素；μclose to Y（u）代表元素u隶属于“close to Y”的程度；β为一个调节值，β越大，对于同一个u来说，u隶属于“close to Y”的程度越大。模糊集“close to Y”的隶属函数如图1所示。

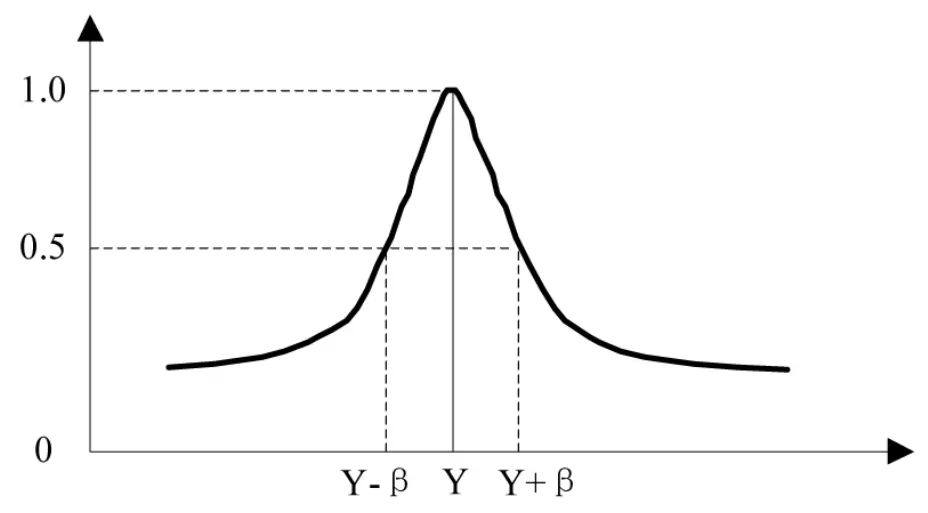
图1 模糊集“close to Y”的隶属函数

基于该思想，假设数值属性A中包含的值为{v1，v2，…，vn}，根据上述“close to Y”的隶属函数，两个数值vi和vj之间的语义相似度可由下式计算：

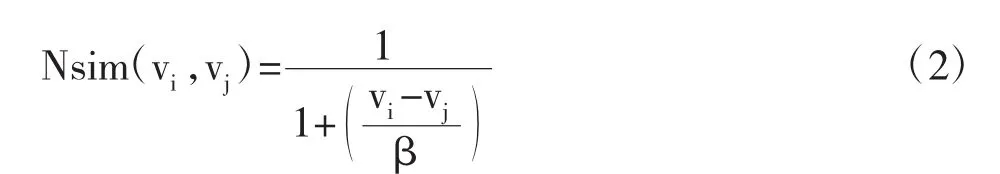
其中，β=1.06σn-1/5，σ是数值属性A上所有值的标准差，n为A中所有值的个数。从式（2）可以看出，vi与vj在数值上越接近，则Nsim( )的值越接近1。

在此基础上，通过合并两个向量表中所有对应属性上的相似度，可获得这两个向量表对应的学生之间的耦合关系度。然而，在评估两个向量表之间相似度过程中，向量表中每个属性的重要程度不尽相同。例如，家庭收入与父母政治面貌相比，前者对学生相似度评估和类别划分显得更重要。因此，两个不同学生之间的耦合关系度，应该是两个向量表中不同权重值之间的相似度之和，

其中，S1和S2代表两个不同学生；V1和V2分别是对应学生S1和S2的两个向量表（假设每个向量表都包含m个属性）；Valuesi是向量表中第i个属性对应的值信息；W（Ai）是属性Ai的权重

（三）耦合关系度的实现算法

根据上述耦合关系评估方法，下面给出相应的实现算法（算法1）。算法首先抽取出学生背景信息数据集中的所有不同的学生对，然后按照上述耦合关系评估方法得出不同学生对之间的耦合关系度。由于学生之间的耦合关系矩阵是对称的，因此只需计算上半矩阵。

算法1 学生耦合关系度实现算法输入：学生个数-n，背景信息属性个数-m，属性值-V a l u e s，属性权重-W输出：学生耦合关系度矩阵M a t r i x 1.M a t r i x←φ；2.f o r i=1...n-1 d o 3.i V a l u e s=g e t A t t r i b u t e V a l u e s（i）；4.f o r j=i+1...n d o 5.j V a l u e s=g e t A t t r i b u t e V a l u e s（j）；6.f o r k=1...m d o 7.S i m[k]=S i m（i V a l u e s［k］，j V a l u e s［k］）；8.e n d f o r m 9.S i m D e g r e e=∑s i m［k］×W［k］；i=1 1 0.M a t r i x［i］［j］=S i m D e g r e e；1 1.M a t r i x［j］［i］=M a t r i x［i］［j］；1 2.e n d f o r 1 3.e n d f o r 1 4.r e t u r n M a t r i x.

根据上述算法，可以得到所有不同学生之间的耦合关系度，然后存储在结构为{学生1，学生2，耦合关系度}的学生耦合关系度表中，并在（学生1，学生2）属性上建立索引以便于检索。下面讨论如何根据学生之间的耦合相似度选取有代表性的学生以及对学生群体进行划分。

二、学生的典型程度度量

根据学生之间的耦合关系度，本文提出一种基于概率密度的典型化分析方法，目的是从学生集合中找出若干具有代表性的学生（即典型学生），然后对学生群体进行划分，使得每个典型学生能够代表其所在群体的总体特征，从而为精准分析不同类别学生的就业意向及影响因素提供数据基础。

传统的聚类分析与本文所提的典型程度分析具有一定相关性，聚类分析是将集合中的对象划分成若干类别，使同一类别中对象之间的相似度尽可能大，不同类别对象之间的相似度尽可能小，而典型化分析是要找出代表性对象[8]。一些研究工作把均值点（means）或中心点（medoids）作为一个聚类的代表，然而有时均值点或中心点可能并不是聚类中的代表[9]。如图2所示，对象B和C分别是集合的均值点和中心点，但分布在A周围的对象要比B和C的多，因此A要比B和C更具有代表性。在学生群体中，需要根据学生之间的耦合关系度，找出具有代表性的学生（类似于图2中的点A），并据此对学生群体进行划分。

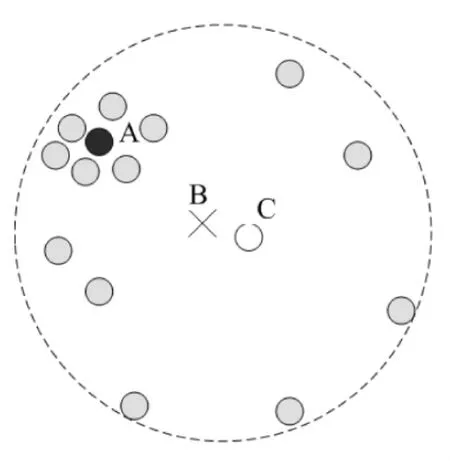
图2 中心点、均值点和典型点对象的区别

概率密度是分析集合中某个对象典型程度的核心方法。本文提出利用概率密度函数计算学生的典型程度，在一个学生群体中，如果与某个学生耦合关系度密切的学生越多，说明其越具有代表性。根据学生之间的耦合关系度，可将学生群体中的所有学生看成是一个空间中的点集合，其中每个点代表一个学生，学生之间的直线距离代表一对学生之间的耦合关系距离。这样就可以用概率密度估计方法来评估学生群体中某个学生的典型程度。本文采用基于高斯核函数的概率密度估计方法。对于学生群体S/，其中一个学生s∈S/的典型程度定义为：T（s，S/）=f（s|S/），其中f（s|S/）是S/上的概率密度分布函数，该函数可用下式计算：

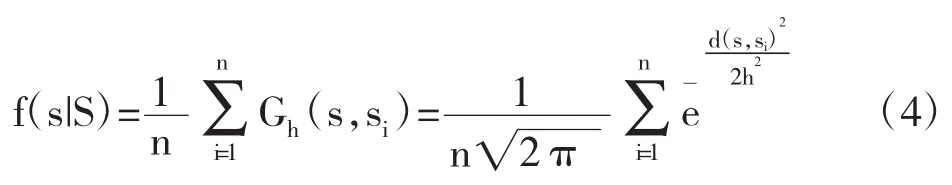
其中，d（s，si）2代表学生s与si之间的耦合关系距离是高斯核函数，n代表中的学生总数。

接下来的问题是，给定学生集合S/（包含n个学生）和所有学生之间的耦合关系距离，目标是选出其中m（m＜＜n）个具有较高典型程度的学生，然后对学生群体进行划分。根据式（4），每计算一个学生的典型程度都需要遍历S/中所有其他学生对其的贡献度，则该算法的时间复杂度为O（n2）。当学生数n很大时，算法需要耗费很多时间，因此需要考虑一种既能快速找出典型代表又具有较高准确性的近似解法。

三、典型学生选取与学生群体划分

本节提出两种典型学生的近似选取及相应的学生群体划分方法，分别是基于阈值的近似选取方法和基于淘汰策略的近似选取方法，这两种方法分别适用于不同情况。

（一）基于阈值的近似选取与学生群体划分方法

基于阈值的近似选取方法的基本思想是，首先构建学生耦合关系距离矩阵，然后根据矩阵中每行的值计算出对应学生的典型程度，从中选出最大典型程度的学生，并把与该学生相似度高于给定阈值的其他学生划分到同一类别。重复执行上述过程，直到所有学生都归到相应类别为止。下面，结合一个实例说明该算法的执行过程。

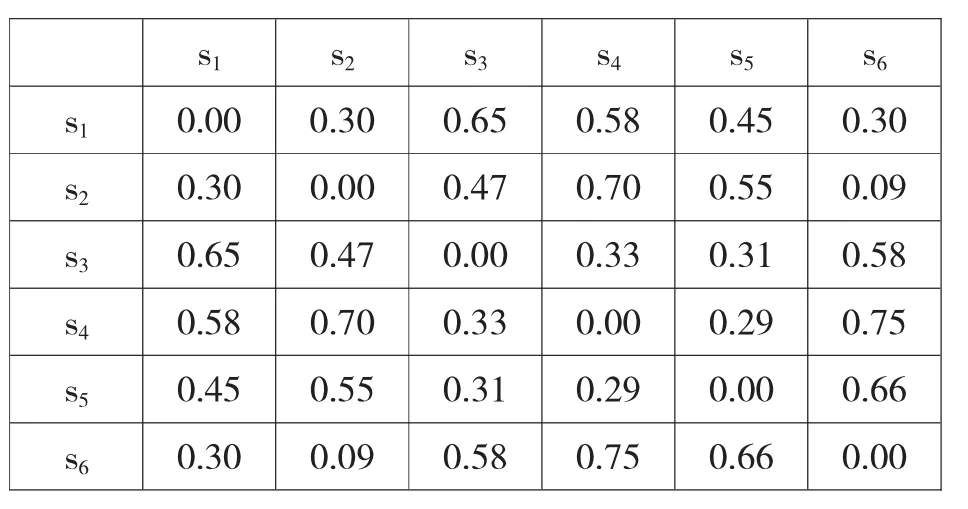
表4 学生耦合关系距离矩阵表

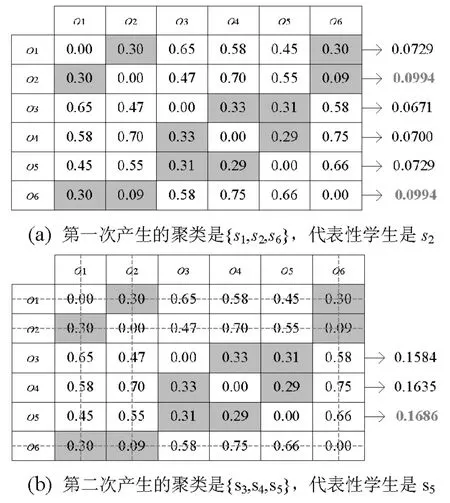
图3 基于耦合关系距离矩阵和概率密度估算的学生聚类方法的例子

假设给定的耦合关系距离阈值是0.35，图3说明了该算法的处理过程。

该算法首先根据学生耦合关系距离矩阵的每一行元素，每个元素代表一对学生之间的耦合关系距离，将距离值不大于给定阈值的学生划分到同一类中。对于图3（a）中显示的学生耦合关系距离矩阵，给定的阈值是0.35，距离矩阵中每一行不大于0.35的元素被标记为灰色，因此每一行中与行首学生耦合关系距离不超过0.35的学生可以划分到一类中。例如，对于矩阵每一行的聚类分别是{s1,s2,s6}，{s2,s1,s6}，{s3,s4,s5}，{s4,s3,s5}，{s5,s3,s4} 和{s6,s1,s2}。之后，对于同一类中的每个学生，通过使用高斯核函数计算出每个学生的概率密度，概率密度最大的学生可以用来代表该类中的其它学生。如图3（a）所示，学生s2和s6的概率密度值最大，都是0.0994，因此随机选取学生s2作为第一个典型，这样能够用s2表示的对象是s1和s6（他们到s2的距离分别是0.30和0.09）。在下次循环时，被s2代表的学生从矩阵中移除，然后继续从重新构成的矩阵中选出典型学生。如图3（b）所示，剩余的学生分别是s3，s4和s5，首先选取每一行中不大于阈值0.35的学生，之后计算与每一行相关的学生的概率密度值，最大的概率密度值是0.1686，因此学生s5被选作是第二个代表，相应地学生s3和s4被划分到s5所代表的类别中。至此，所有的学生都被从矩阵中移除了，算法终止。最终，上述学生群体被分为两类，分别是{s1,s2,s6}和{s3,s4,s5}，每一类中的典型学生分别是s2和s5。

（二）基于淘汰策略的选取与划分方法

该方法的基本思想是基于淘汰策略[10]，逐步选取典型学生和划分学生群体，其基本过程如下：

1.先把学生集合T随机划分成若干小组，每个小组包含u个学生，这样可将T划分成n/u个小组，然后计算每个小组内所有学生的典型程度并从中选取一个具有最高典型程度的学生，这些学生构成一个新的集合，然后从T中去除其他学生。

2.对于得到的新集合，重复上述过程，直到集合T中只剩下一个学生为止，将该学生放入典型学生候选集合中（上述过程记为一次选取过程）。

3.为了尽可能确保选取的准确性，将上述选取过程重复执行v次（记为一轮），这样候选集合中最多存储v个学生，然后在最初的学生集合T上计算这v个学生的典型程度，最后输出一个具有最高典型程度的学生作为当前轮次的选取结果，并从T中去除该学生。上述整个过程重复k轮，这样就能找到k个典型学生。

4.根据学生之间的耦合关系度，把剩余学生划分到与其关系最近的典型学生类别中。

以上两种近似算法各具特点，能够分别适用于不同情况。第一种需要给定耦合关系度阈值来控制聚类个数，这种算法能够明确知道每个聚类所包含的学生之间相似度，但不确定能够划分成多少个聚类；第二种直接给定k值来控制聚类个数，这种算法适用于明确指定需要将学生群体划分成多少个聚类，但不知道每个聚类中成员之间的相似度。

四、结果分析

本节主要介绍实验数据集和分析结果。本文的调查问卷涉及1000名大学生，这些学生的家庭住址分别来自一线城市、省会城市、地级市和农村以及西部地区，他们的家庭年均收入从几千到几十万不等，专业课平均成绩从40以上到90以下成正态分布，父母从事的职业有国家机关、企事业单位、个体和农民等（涵盖了大多数的职业），调查对象具备多样性和完备性。在该数据集上，我们开展了学生耦合相似度评估方法的准确性验证、典型学生近似选取算法的误差率测试，以及学生群体划分的合理性验证。

算法2.T o p-k典型学生的近似选取算法输入：学生集T，验证次数v，正整数k，小组大小u输出：t o p-k个典型学生1.f o r i=1 t o k d o 2.f o r i=1 t o v d o 3.r e p e a t 4.划分T成为若干小组g，每个小组有u条学生5.f o r e a c h小组g d o 6.计算g中每个学生在g中的典型程度7.从g中选出最典型的学生，并将g中其他学生从T中移除8.e n d f o r 9.u n t i l T中仅有一个学生1 0.把得到的最典型学生放入候选集合中1 1.e n d f o r 1 2.在T上计算候选集合中每各学生的典型程度，输出一个最典型学生作为第i次选出的典型学生1 3.e n d f o r 1 4.r e t u r n t o p-k个典型学生及与相应的群体划分

（一）学生耦合关系度评估方法的准确性验证

本文使用用户调查方法验证提出的学生耦合关系度评估方法的准确性。邀请了10个志愿者（博士生、硕士生和教师等）从调研学生集合中各选取10个学生，对于每个选取的学生si，分别利用本文提出的耦合评估方法（CSIM）、严格关系匹配方法（RSIM）和随机选取方法（RANDOM）从学生集合中获得前10个相似学生，最终合成一个包含30个与给定学生si背景信息相似和不相似的学生集合Si。在此基础上，把Si和si提供给志愿者，由志愿者从Si中标出前10个与si背景信息最接近的学生，并且从以下两方面衡量选择的学生s'与给定学生s的相似性：

1.学生s'与s在某些属性上有重叠的内容，则二者在一定程度上相似；

2.学生s'与s在内容上没有重叠，却具有相关关系。例如，s'与s的父母学历都是本科以上，家庭收入都是十万元以上，家庭住址都在东南沿海地区，专业课平均成绩比较接近等。

本文用志愿者标注的相关学生与不同方法选取的相关学生的重叠程度来衡量不同方法的准确性。图4给出了在调研学生数据集上CSIM、RSIM和RANDOM方法的准确性对比。

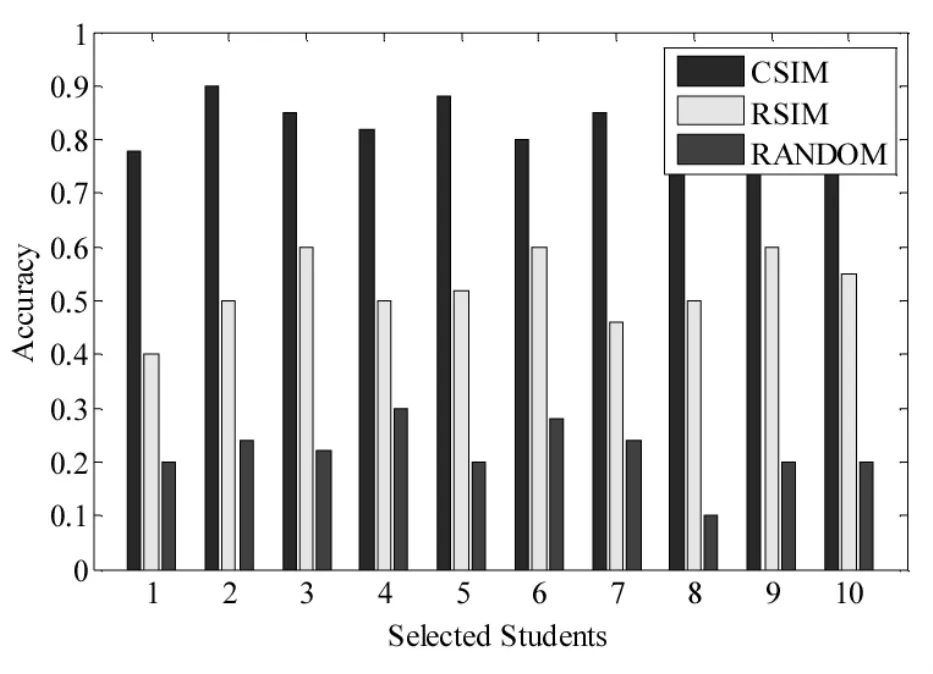
图4 学生数据集上的CSIM，RSIM，and RANDOM方法的准确性对比

从上图可以看出，CSIM方法的准确性在很大程度上高于RSIM和RANDOM方法。CSIM、RSIM和RANDOM在数据集上的平均准确性分别为0.84和0.52和0.22。这是因为CSIM是在向量空间模型上分别计算学生在不同维度上的相关度，并且考虑了属性权重以及数值上的接近关系，而RSIM方法仅考虑两个学生背景信息表中内容完全重合的程度，没有考虑数值上的接近关系和属性的重要程度。由此可见，本文方法得到的学生之间的耦合关系度更为准确合理。

（二）典型学生近似选取算法的误差率测试

本文用误差率（error rate，E）来衡量典型学生近似选取算法的准确性。给定一个学生，令R（t）代表由准确选取算法返回的前k个典型学生，t）代表由近似选取算法返回的前k个典型学生，在此基础上，误差率定义如下：

在该实验中，式（5）的 k 值分别取 5、10、15、20、25和30，第一种近似选取算法的阈值设置为能够得到上述k值的聚类个数，第二种近似选取算法的参数u和v分别设置为u=20，v=5（根据实验测试发现，当验证次数v超过4时，算法的效果提升非常小，因此把v值设置为5），数据集大小设置为1000个学生。图5给出了两种近似选取算法在数据集上的平均误差率（分别取10次测试误差率的平均值）。

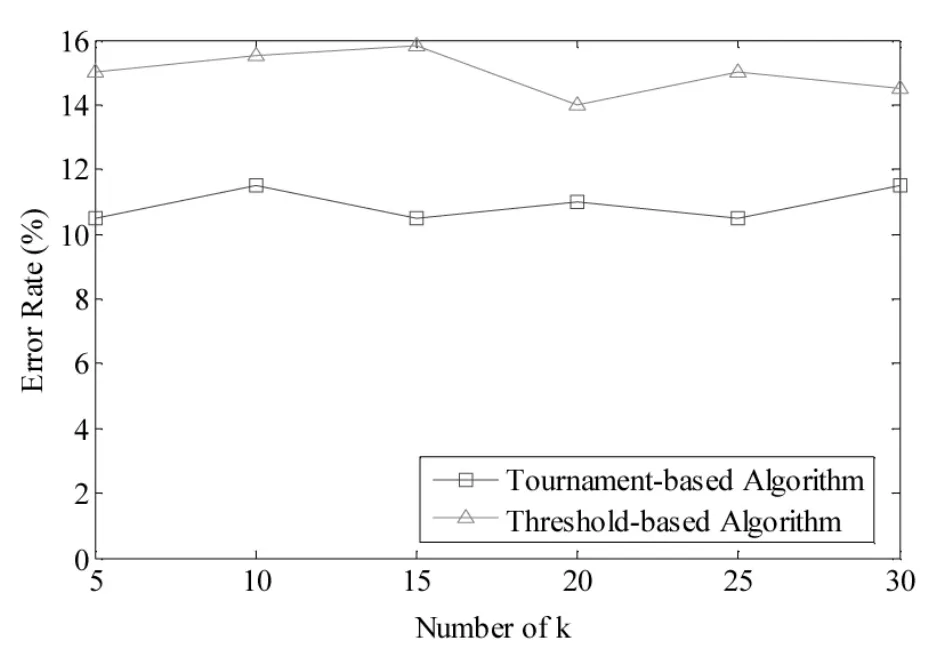
图5 当k值变化时两种近似选取算法的平均误差率

实验结果表明，两种近似选取算法的平均误差率分别为15%和11%，基于淘汰算法的误差率较低。因此，在不要求知道聚类内部相似度的情况下，可以优先采用基于淘汰算法的典型学生选取及在此基础上的学生群体划分方法。另外，从图中还可以看出，算法的误差率与k值关系不大（也就是说对k值的变化不敏感），这是因为算法的每一轮选取都经过v次验证，然后再经过k轮选取后得到的top-k个结果。

图6给出了当数据集中的学生数发生变化时对基于淘汰策略的近似选取算法准确性的影响（这里将k值固定为10，u固定为20）。

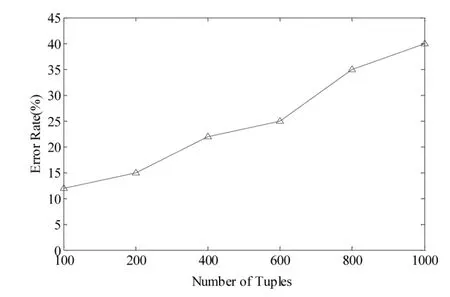
图6 学生数据集大小变化时基于淘汰策略的近似选取算法的误差率

可以看出，当数据集增大（即包含的学生数增多）时，算法误差率也随之增大，这是因为当参数u（每个小组中的学生数）固定情况下，数据集中的学生数越多，那么从每个小组中选出的最典型学生就越有可能是有偏差的（即与全局典型学生的差距越大）。

五、结论

由于学生的就业偏好及其影响因素与学生背景信息具有很大相关性，因此需要根据学生背景信息对学生群体进行聚类，进而对学生就业偏好及影响因素进行精准分析。本文提出了根据学生背景信息进行学生耦合关系度的评估方法，经数据分析与实验验证，该方法能够较为准确量化学生之间的相似度，区分出不同学生之间的接近程度。在学生耦合关系度基础上，提出了利用概率密度估计方法评估学生典型程度的方法，学生群体中有一部分是具有代表性的典型学生，对其进行准确识别有助于对学生群体划分和对特定群体的特征抽取。为了减少计算复杂度，还提出了两种典型学生的近似选取算法，经试验测试分析，两种算法各具优缺点，基于淘汰策略的近似选取算法在误差率方面优于基于阈值的近似选取算法，但是不能体现聚类成员之间的相似度。根据选出的典型学生，可将其他学生归到相应的类别。每个类别中的学生都具有与该类典型学生相似的背景信息。

本文研究的大学生生群体划分方法为精准分析大学生的就业偏好和影响因素提供了高质量的基础数据。

［1］喻名峰，陈全文，李恒全.回顾与前瞻：大学生就业问题研究十年［J］.高等教育研究，2012，33（2）：79-86.

［2］风笑天.我国大学生就业研究的现状与问题［J］.南京大学学报，2014（1）：60-69.

［3］尹若珺，王馨第，张文颖.大学生就业质量影响因素调查与研究——以吉林大学为例［J］.中国大学生就业，2016（7）：44-49.

［4］柯羽.高校毕业生就业质量评价指标体系的构建［J］.中国高教研究，2007（7）：82-84.

［5］白亮，万明钢.西部地区少数民族大学生就业问题研究——基于教育供给侧的分析［J］.高等教育研究，2016（7）：21-26.

［6］段晓丹.农村大学生“就业难”问题研究［J］.淮北职业技术学院学报，2016（4）:102-103.

［7］张抗私，盈帅.性别如何影响就业质量?——基于女大学生就业评价指标体系的经验研究［J］.财经问题研究，2012（3）:83-90.

［8］Gan G J，Ma C Q，Wu J H.Data clustering：Theory，algorithms，and applications［M］.Philadelphia：Society for industrial and Applied Mathematics，2007.

［9］Bouveyron C，Brunet-Saumard C.Model-based clustering of high-dimensional data：A review［J］.Computational Statistics and Data Analysis，2014，71（3）：52-78.

［10］Xiangfu Meng，Longbing Cao，Xiaoyan Zhang，Jingyu Shao.Top-k coupled keyword recommendation for relational keyword queries.Knowledge and Information Systems.Online publication.DOI：10.1007/s10115-016-0959-3.