多层单向耦合星形网络的特征值谱及同步能力分析∗

孙娟李晓霞 张金浩申玉卓李艳雨

1)(省部共建电工装备可靠性与智能化国家重点实验室(河北工业大学),天津 300130)

2)(河北省电磁场与电器可靠性重点实验室(河北工业大学),天津 300130)

多层单向耦合星形网络的特征值谱及同步能力分析∗

孙娟1)2)李晓霞1)2)†张金浩1)2)申玉卓1)2)李艳雨1)2)

1)(省部共建电工装备可靠性与智能化国家重点实验室(河北工业大学),天津 300130)

2)(河北省电磁场与电器可靠性重点实验室(河北工业大学),天津 300130)

多层星形网络,有向网络,特征值谱,同步能力

1 引 言

近几年,复杂网络研究主要集中在网络的拓扑结构与其动力学行为之间的关系[1−4]、扩散动力学[5−9]、同步[10−14]等方面.目前大多数复杂网络的研究都集中在单个网络[15−27],然而现实世界中各类系统之间并不是独立的,而是相互联系的.研究结果表明,单个网络建模的方法一般不足以确定出现在实际复杂系统中的多层网络间的真正的相互依存关系.比如,一些不同社交网络的用户关系[28]、运输系统[29]以及大脑的学习型组织[30].尽管多层网络的研究还处于起步阶段,但已经涌现出一些有影响力的研究成果[31,32],这将是复杂网络理论的重要研究方向.

研究复杂网络的终极目标之一是理解网络拓扑结构对物理过程的影响.网络上的同步现象是一项重要的研究课题[33,34].同步现象大量出现在我们的生活中,如掌声同步、路由器同步、萤火虫同时闪烁、物理振子以及生物振子的同步等,在物理、化学、生物、工程技术、经济以及社会科学等领域都观察到了各种各样的同步现象[35−39].复杂网络作为一个载体展示了丰富多彩的网络同步现象,不同领域的学者从不同的角度对复杂网络同步进行了深入研究.

为了研究更接近于实际复杂网络的同步能力,学者们提出了一种基于多层网络的扩散动力学方程的超拉普拉斯矩阵结构,根据其特征值谱来分析网络同步能力[40].根据主稳定性函数方法,复杂系统的非线性动力学行为与网络的拉普拉斯矩阵的第二个特征值有关[41],在扩散过程中,收敛于最大熵状态[42],而且耦合网络的拉普拉斯矩阵的最大特征值对网络的同步稳定性具有决定性影响[43,44].文献[45,46]研究了典型的规则两层星形网络,提出并严格推导出两层星形网络的特征值谱,并分析了同步能力,但由于实际复杂网络更接近于有向网络,本文即在此基础上研究了更具一般性的多层有向星形网络的特征值谱及同步能力.首先,严格推导出三层单向耦合的星形网络的特征值多项式,分别分析了在同步域无界和有界两种情况下,网络层数、每层网络节点数、层内耦合强度、层间耦合强度(层间中心节点之间的耦合强度和层间叶子节点之间的耦合强度)与网络同步能力的关系.其次,进一步严格推导出多层单向耦合的星形网络的特征值多项式以及特征值谱,分析了在同步域无界和有界两种情况下,网络层数、每层网络节点数、层内耦合强度、层间耦合强度(层间中心节点之间的耦合强度和层间叶子节点之间的耦合强度)与网络同步能力的关系.最后,分析各个参数对网络同步能力的影响并进行了仿真验证.

2 模型与方法

2.1 模 型

M层网络中第K层、第i个节点的动力学方程如下:

我们假设多层网络为M层网络,每层有N个节点.α层的层内连接强度矩阵W(α)∈RN×N,S(α)∈RN×N为层内点强度的对角矩阵,层的层内拉普拉斯矩阵为L(α)=S(α)−W(α), 假设多层网络层间的所有节点的层间连接完全一致,我们定义WI∈RM×M为每两层网络的层间连接强度矩阵,SI∈RM×M为每两层网络的层间点强度对角矩阵,每两层网络的层间拉普拉斯矩阵为LI=SI−WI.

我们得到整个网络的超拉普拉斯矩阵:L=LL+LI.我们把L分成两部分,LL为层内的超拉普拉斯矩阵,LI为层间的超拉普拉斯矩阵.LL为各层内拉普拉斯矩阵的直和,

LI为层间拉普拉斯矩阵与M×N的单位矩阵的Kronecker积,

2.2 方 法

本文采用主稳定性函数法来判定网络的同步能力的稳定性.一个由N个相同的动力学系统˙Xi=f(Xi)为节点所构成的连续时间耗散耦合动态网络,其状态方程如下:

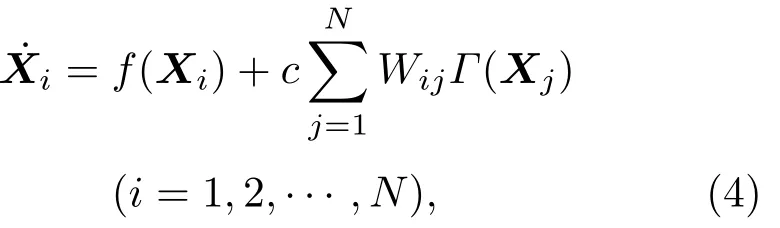
主稳定性函数法是研究线性耦合同步稳定性问题的一种主要方法,并被广泛采用.下面主要详细介绍主稳定性函数法.我们将连续时间动态网络(4)式关于同步流形S(t)进行线性稳定性分析.令δi为第i个节点状态的变分,可以得到下面的变分方程:

这里Jf和JH分别是f(X)和H(X)关于同步流形S的Jacobi矩阵,通常要求为有界.令则(5)式可写为矩阵形式:

下面根据Lyapunov指数法来判断同步流形的稳定性.考虑到方程中只有λk和ηk与k有关,当外耦合矩阵W为非对称时,其特征值可能是复数,故定义主稳定性方程为

其最大Lyapunov指数γmax是实变量α和β的函数,称为动力学网络的主稳定性函数.已知一个给定的耦合强度c,在(α,β)所在的复平面上对应一个点cλk,如果该点对应的最大Lyapunov指数γmax为正数时,则该特征态为不稳定态;反之,则该特征态为稳定态.如果对应所有的特征态λk(k=2,3,···,N), 其所有点对应的最大Lyapunov指数γmax均为负数时,那么认定在该耦合强度c下,整个网络的同步流形是渐近稳定的.

根据主稳定函数方法,本文网络模型的同步能力由L的非零最小特征值λ2和最大特征值λmax决定[47−50].当同步域无界时,网络的同步能力由λ2决定,并与λ2成正比;当同步域有界时,网络的同步能力由λmax/λ2决定,此时网络的同步能力与r=λmax/λ2成反比.对于同步化区域为空集的情况,无论耦合强度c怎么改变都不能实现网络的同步,所以无需讨论该情况.

3 特征值谱及同步能力分析

3.1 三层单向耦合星形网络的结构

本节首先严格推导三层单向耦合的星形网络的特征值谱,其中单向耦合包含叶子节点向中心节点的单向耦合和中心节点向叶子节点的单向耦合,耦合模型如图1(a)和图1(b)所示,层间耦合方式如图2所示.图1(a)的每层星形网络内,叶子节点向该层中心节点耦合强度为a;图1(b)的每层星形网络内,中心节点向该层叶子节点耦合强度为a;图2中每两层网络间叶子节点与叶子节点一一对应耦合,中心节点与中心节点一一对应耦合,耦合方式为双向耦合,叶子节点之间耦合强度为d,中心节点之间耦合强度为d0.

图1 (网刊彩色)(a)叶子节点向中心节点的单向耦合;(b)中心节点向叶子节点的单向耦合;黑色虚线表示每两层间叶子节点耦合,红色虚线表示每两层间中心节点耦合,层内耦合强度为a,层间叶子节点之间的耦合强度为d,层间中心节点之间的耦合强度为d0Fig.1.(color online)(a)The coupling model is that leaf nodes point to the hub node;(b)the coupling model is that the hub node point to leaf nodes.The black dotted line represents the coupling connection between the leaf nodes of every two layers of the network,the red dotted line represents the coupling connection between the hub nodes of every two layers of the network,the intralayer coupling strength a the inter-layer leaf nodes coupling strength d,the interlayer hub nodes coupling strength d0.

图2 (网刊彩色)层间耦合方式,每两层叶子节点之间一一对应双向耦合,每两层中心节点之间一一对应双向耦合;黑色虚线表示层间叶子节点之间的耦合连接,红色虚线表示层间中心节点之间的耦合连接Fig.2.(color online)The coupling model between the layers.The coupling between the leaf nodes of every two-layer of network is one-to-one bidirectional coupling,and the coupling between the hub nodes of every two-layer of network is one-to-one bidirectional coupling;the black dotted lines represent the interlayer leaf nodes,and the red dotted lines represent the coupling between the inter-layer hub nodes.

3.2 三层单向耦合星形网络的特征值谱及同步能力分析

首先,这里我们假设三层网络的每层网络的拓扑结构是完全一致的星形网络,每两层网络间叶子节点之间、中心节点之间分别都是一一对应耦合;每层网络的节点数都为N,整个网络层数为M,层内耦合强度为a,层间中心节点之间的耦合强度为d0,层间叶子节点之间的耦合强度为d.对于简单有向图G,其拉普拉斯矩阵L(G)=S(G)−W(G),S(G)为顶点出度的对角矩阵,W(G)=[aij]为其邻接矩阵,aij为节点Vi到Vj的边的权值[51].由此得到的三层叶子节点向中心节点的单向耦合星形网络的超拉普拉斯矩阵为

三层中心节点向叶子节点的单向耦合星形网络的超拉普拉斯矩阵为

三层中心节点向叶子节点的单向耦合星形网络的超拉普拉斯矩阵的特征值多项式为故特征值为:

在实际网络中,节点数N是非常大的,远远大于层内耦合强度a和层间节点之间的耦合强度d与d0.其同步能力的强弱根据同步域无界和有界两种情形来考虑,即讨论非零最小特征值λ2(值越大同步性越强)与r=λmax/λ2(值越小同步性越强).

三层叶子节点向中心节点单向耦合的星形网络,当同步域无界时,网络的同步能力由λ2=min{a,3d0}决定;当同步域有界时,网络的同步能力由r=(a+3d)/min{a,3d0}决定,而无论是同步域无界还是有界,网络的同步能力都与节点数无关.

三层中心节点向叶子节点单向耦合的星形网络,当同步域无界时,网络的同步能力由λ2=3d决定;当同步域有界时,网络的同步能力由r=[(N−1)a+3d0]/3d决定.

3.3 多层单向耦合星形网络的特征值谱及同步能力分析

本文进一步推导出多层单向耦合星形网络的超拉普拉斯矩阵及特征值多项式,多层叶子节点向中心节点单向耦合的星形网络的超拉普拉斯矩阵为

多层中心节点向叶子节点单向耦合的星形网络的超拉普拉斯矩阵为

多层中心节点向叶子节点单向耦合的星形网络的特征值多项式为:故特征值为

多层叶子节点向中心节点单向耦合的星形网络的同步能力,按同步域为无界和有界两种情形分别讨论,当同步域无界时,网络的同步能力由λ2=min{a,Md0}决定;当同步域有界时,网络的同步能力由r=(a+Md)/min{a,Md0}决定,除了d,a,d0,多层网络的层数对网络的同步能力也会产生影响.

多层中心节点向叶子节点单向耦合的星形网络,按同步域为无界和有界两种情形分别讨论,当同步域无界时,网络的同步能力由λ2=Md决定;当同步域有界时,网络的同步能力由r=[(N−1)a+Md0]/Md决定.除了N,d,a,d0,网络的同步能力也受到多层网络的层数的影响.

4 数值仿真及结果

4.1 三层叶子节点向中心节点单向耦合的星形网络的同步能力仿真

同步域无界时,λ与a,3d0中的最小值有关;同步域有界时,同步能力由r=(a+3d)/min{a,3d0}来决定,网络的同步能力与N无关.仿真情况归纳见表1.

1)同步域无界

同步域无界、a<3d0时,λ2与a有关;a>3d0时,λ2与d0有关.分别变化a和d0,所得到的λ2如图3所示.λ2随着a的增大而增大,随着d0的增大而增大,同步能力增强,增大层间中心节点之间的耦合强度更有利于提高同步能力,这是因为三层网络类似于三个聚类的社团结构,聚类块间连接紧密,从而使同步能力变得更强.最后,从图3我们可以得到:当同步域无界时,对于层内耦合强度和层间中心节点之间的耦合强度,同步能力依赖于较弱的一方;在两种耦合强度同步改变时,层间中心节点之间的耦合强度对同步能力产生的影响更大一些.

表1 对于三层叶子节点向中心节点单向耦合的星形网络,λ2,r= λmax/λ2随d,a,d0的变化Table 1.When the coupling model is that leaf nodes point to the hub node for three-layer star networks,λ2 and r= λmax/λ2changes with d,a,d0.

图3 (网刊彩色)对于三层叶子节点向中心节点单向耦合的星形网络,λ2随层内耦合强度a的变化(红色实线),a<3d0;λ2随层间中心节点之间的耦合强度d0的变化(蓝色实线),a>3d0Fig.3.(color online)When the coupling model is that leaf nodes point to the hub node for three-layer star networks,λ2change with the intra-layer coupling strength a(red solid line),a<3d0;λ2change with inter-layer coupling strength between the hub nodes d0(blue solid line),a>3d0.

2)同步域有界

同步域有界、a<3d0时,同步能力由r=1+3d/a决定;a>3d0时,同步能力由r=(a+3d)/3d0决定.

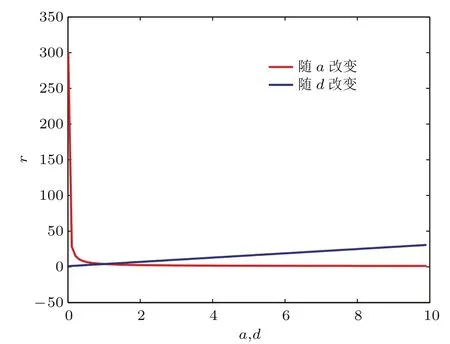
图4 (网刊彩色)对于三层叶子节点向中心节点单向耦合的星形网络,r随层内耦合强度a的变化(红色实线);r随层间叶子节点之间的耦合强度d的变化(蓝色实线);其中a<3d0Fig.4.(color online)When the coupling model is that leaf nodes point to the hub node for three-layer star networks,r change with the intra-layer coupling strength a(red solid line)and the inter-layer coupling strength between the leaf nodes d(blue solid line),a<3d0.

2⃝a>3d0时,取d=1,d0=0.01,变化a,取a=1,d0=0.01,变化d;取d=1,a=1,变化d0.得到的r如图5所示.r随a的增大而增大,r随d的增大而增大;r随d0增大呈指数减小.层内耦合强度越小,层间叶子节点之间的耦合强度越小,层间中心节点之间的耦合强度越大,同步能力变得越强.最后,从图5(a)我们可以得到:在上述假定条件下,当层内耦合强度和层间叶子节点之间的耦合强度值取1时,同步能力相等.从图5(b)和图4我们可以得到:当同步域有界时,网络的同步能力依赖于层内耦合强度和层间中心节点之间的耦合强度中较弱的一方.

图5 (网刊彩色)对于三层叶子节点向中心节点单向耦合的星形网络 (a)r随层内耦合强度a的变化(红色实线)以及r随层间叶子节点之间的耦合强度d(蓝色实线)的变化;(b)r随层间中心节点之间的耦合强度d0的变化;其中a>3d0Fig.5.(color online)When the coupling model is that leaf nodes point to the hub node for three-layer star networks,(a)r change with the intra-layer coupling strength a(red solid line)and the inter-layer coupling strength between the leaf nodes d(blue solid line),respectively;(b)r change with the inter-layer coupling strength between the hub nodes d0;a>3d0.

4.2 三层中心节点向叶子节点单向耦合的星形网络的同步能力的仿真

三层中心节点向叶子节点单向耦合的星形网络,当同步域无界时,网络的同步能力由λ2=3d决定;当同步域有界时,网络的同步能力由r=[(N−1)a+3d0]/3d决定.仿真情况归纳于表2.

表2 对于三层中心节点向叶子节点耦合的星形网络,λ2和r=λmax/λ2随N,M,d,a,d0的变化Table 2.When the coupling model is that the hub node point to leaf nodes for three-layer star networks,λ2and r= λmax/λ2changes with N,M,d,a,d0.

1)同步域无界

λ2与d有关,变化d,如图6所示,λ2随d的增大而增大.层间叶子节点之间的耦合强度增大,同步能力越强.中心节点向叶子节点单向耦合的三层星形网络的超拉普拉斯矩阵的非零最小特征值是一定的,不需要讨论,它与层间叶子节点之间的耦合强度有关,而与层内耦合强度和层间中心节点之间的耦合强度无关.

图6 (网刊彩色)对于三层中心节点向叶子节点耦合的星形网络,λ2随层间叶子节点之间的耦合强度d的变化Fig.6.(color online)When the coupling model is that the hub node point to leaf nodes for three-layer star networks,λ2change with the inter-layer coupling strength between the leaf nodes d.

2)同步域有界

网络的同步能力由r=[(N−1)a+3d0]/3d决定.取N=200,d=d0=1,变化a;取N=200,a=d0=1,变化d;取N=200,d=a=1,变化d0;取a=d=d0=1,变化N;得到的r如图7所示.r随a的增大而增大;r随d的增大呈指数减小;r随d0的增大而增大;r随N的增大而增大.层内耦合强度越小,层间叶子节点之间的耦合强度越大,层间中心节点之间的耦合强度越小,网节点数越少,网络的同步能力变的越强.从图7我们得到:在上述假定条件下,网络的同步能力更依赖于层间叶子节点之间的耦合强度,而层间中心节点之间的耦合强度对网络同步能力的影响微乎其微.

图7 (网刊彩色)对于三层中心节点向叶子节点耦合的星形网络,(a)r随层内耦合强度a的变化(红色实线),r随层间叶子节点之间的耦合强度d的变化(蓝色实线),r随层间中心节点之间的耦合强度d0的变化(黑色实线);(b)r随节点数N 的变化Fig.7.(color online)When the coupling model is that the hub node point to leaf nodes for three-layer star networks,(a)r change with the intra-layer coupling strength a(red solid line),the inter-layer coupling strength between the leaf nodes d(blue solid line),and the inter-layer coupling strength between the hub nodes d0(black solid line),respectively;(b)r change with the number of nodes N.

4.3 多层叶子节点向中心节点单向耦合的星形网络的同步能力的仿真

多层叶子节点向中心节点单向耦合的星形网络,当同步域无界时,网络的同步能力由λ2=min{a,Md0}决定;当同步域有界时,网络的同步能力由r=(a+Md)/min{a,Md0}决定;网络的同步能力与N无关.仿真情况归纳于表3.

情况 3 v7,v8全染颜色1,v2,v6染1,v4只能染2,则可继续用上述方法将穷点v3改染为1, 并用3来染v。

表3 对于多层叶子节点向中心节点单向耦合的星形网络,λ2和r=λmax/λ2随M,d,a,d0的变化Table 3.When the coupling model is that leaf nodes point to the hub node for multilayer star networks,λ2 and r= λmax/λ2changes with N,M,d,a,d0.

1)同步域无界

2)同步域有界

图8 (网刊彩色)对于多层叶子节点向中心节点单向耦合的星形网络,(a)λ2随层间中心节点之间的耦合强度d0的变化;(b)λ2随层数M的变化Fig.8.(color online)When the coupling model is that leaf nodes point to the hub node for multilayer star networks,(a)λ2change with the inter-layer coupling strength between the hub nodes d0;(b)λ2change with the number of layers M.

图9 (网刊彩色)对于多层叶子节点向中心节点单向耦合的星形网络,(a)r随层内耦合强度a的变化(红色实线),r随层间叶子节点之间的耦合强度d的变化(蓝色实线);(b)r随层数M的变化Fig.9.(color online)When the coupling model is that leaf nodes point to the hub node for multilayer star networks,(a)r change with the intra-layer coupling strength a(red solid line)and the inter-layer coupling strength between the leaf nodes d(blue solid line),respectively;(b)r change with the number of layers M.

图10 (网刊彩色)对于多层叶子节点向中心节点单向耦合的星形网络,(a)r随层内耦合强度a的变化(红色实线),r随层间叶子节点之间的耦合强度d的变化(蓝色实线);(b)r随层间中心节点之间的耦合强度d0的变化;其中a>Md0Fig.10.(color online)When the coupling model is that leaf nodes point to the hub node for multilayer star networks,(a)r changes with the intra-layer coupling strength a(red solid line)and the inter-layer coupling strength between the leaf nodes d(blue solid line),respectively;(b)r change with the inter-layer coupling strength between the hub nodes d0;a>Md0.

a>Md0时,网络的同步能力还受到层数的影响.取a=1,d=1,d0=0.01,变化M,得到r(图11).r随着M的增大呈指数减小.层数越少,同步能力越强.我们从图11可以得到:在上述假定条件下,与a

图11 (网刊彩色)对于多层叶子节点向中心节点单向耦合的星形网络,r随层数M的变化,a>Md0Fig.11.(color online)When the coupling model is that leaf nodes point to the hub node for multilayer star networks,r change with the number of layers M,a>Md0.

4.4 多层中心节点向叶子节点单向耦合的星形网络的同步能力的仿真

多层中心节点向叶子节点单向耦合的星形网络,当同步域无界时,网络的同步能力由λ2=Md决定;当同步域有界时,网络的同步能力由r=[(N−1)a+Md0]/(Md)决定.仿真情况归纳于表4.

表4 对于多层中心节点向叶子节点耦合的星形网络,λ2和r=λmax/λ2随N,M,d,a,d0的变化Table 4.When the coupling model is that the hub node point to leaf nodes for multilayer star networks,λ2 and r= λmax/λ2changes with N,M,d,a,d0.

1)同步域无界

λ2与M,d有关,取d=1,改变M;取M=20,变化d.得到的λ2如图12所示.λ2随M的增大而增大,λ2随d的增大而增大.层间叶子节点之间的耦合强度越大,层数越多,网络的同步能力越强.

2)同步域有界

网络的同步能力由r=[(N−1)a+Md0]/(Md)决定.取N=200,M=20,d=d0=1,变化a;取N=200,M=20,a=d0=1,变化d;取N=200,M=20,d=a=1,变化d0;取a=d=d0=1,N=200,变化M.得到的r如图13所示.r随着a的增大而增大,r随着d的增大而减小,r随着d的增大而增大,r随着M的增大而减小.层内耦合强度越小,层间叶子节点之间的耦合强度越大,层间中心节点之间的耦合强度越小,层数越大,网络的同步能力越强.从图13我们得到:在上述假定的条件下,网络的同步能力更依赖于层间叶子节点之间的耦合强度,层间中心节点之间的耦合强度对网络同步能力的影响微乎其微.比较图7(a)与图13可以得到:层内耦合强度和层间耦合强度对网络同步能力的影响可以由三层网络推广到多层网络;对于多层网络,网络的同步能力也依赖于层数.

图12 (网刊彩色)对于多层中心节点向叶子节点耦合的星形网络,(a)λ2随层数M的变化;(b)λ2随层间叶子节点之间的耦合强度d的变化Fig.12.(color online)When the coupling model is that the hub node point to leaf nodes for multilayer star networks,(a)λ2change with the number of layers M;(b)λ2change with the inter-layer coupling strengthbetween the leaf nodes d.

图13 (网刊彩色)对于多层中心节点向叶子节点耦合的星形网络,(a)r随层内耦合强度a的变化(红色实线),r随层间叶子节点之间的耦合强度d的变化(蓝色实线),r随层间中心节点之间的耦合强度d0的变化(黑色实线);(b)r随层数M的变化Fig.13.(color online)When the coupling model is that the hub node point to leaf nodes for multilayer star networks,(a)r change with the intra-layer coupling strength a(red solid line)and the inter-layer coupling strength between the leaf nodes d(blue solid line)and the inter-layer coupling strength between the hub nodes d0(black solid line),respectively;(b)r change with the number of layers M.

取a=d=d0=1,M=20,变化N,得到r(图14).r随着N的增大而增大.节点数越少,同步能力越强.比较图7(b)和图14可以得到:节点数对网络同步能力的影响与层数无关;节点数对网络同步能力的影响可以由三层网络推广到多层网络.

图14 (网刊彩色)对于多层中心节点向叶子节点耦合的星形网络,r随节点数N的变化Fig.14.(color online)When the coupling model is that the hub node point to leaf nodes for multilayer star networks,r change with the number of nodes N.

5 讨论与结论

本文在理论上严格推导出三层、多层单向耦合星形网络的超拉普拉斯矩阵,得到其特征值谱,并分析了同步能力.对于叶子节点向中心节点耦合的三层及多层星形网络:当同步域无界时,随着层内耦合强度和层间中心节点之间的耦合强度的增大会使同步能力增强,且该影响可以由三层网络推广到多层网络;而对于多层网络,层数的增大也会使同步能力增强.当同步域有界时,在层内耦合强度较弱的情况下,层内耦合强度的增大会使同步能力增强,层间叶子节点之间的耦合强度和层数的增大会使同步能力变弱.在层间中心节点之间的耦合强度较弱的情况下,层间中心节点之间的耦合强度和层数的增大会使同步能力增强,而层内耦合强度和层间叶子节点之间的耦合强度的增大反而会使同步能力变弱.对于中心节点向叶子节点耦合的三层及多层星形网络:当同步域无界时,层间叶子节点之间的耦合强度和层数的增大会使同步能力增强;当同步域有界时,层间叶子节点之间的耦合强度和层数的增大会使同步能力增强,而层内耦合强度、节点数和层间中心节点之间的耦合强度的增大反而会使同步能力减弱.本文结论与文献[45]的结论部分一致,单向耦合的多层星形网络与双向耦合的两层星形网络在结构连接方式上具有一定的联系.相同之处在于:当同步域有界时,文献[45]和本文的叶子节点向中心节点耦合的三层及多层星形网络在层内耦合强度较弱的情况下,都得出层内耦合强度的增大会增强网络的同步能力,层间叶子节点之间的耦合强度的增大会减弱网络的同步能力.通过比较各参数对单向耦合的多层星形网络和双向耦合的两层星形网络同步能力的影响,也得出它们之间的一些不同之处:文献[45]设定层间中心节点之间的耦合强度d0和层间叶子节点之间的耦合强度d相等,在同步域有界的情况下,文献[45]讨论的是层内耦合强度较弱的情况和层间叶子节点之间的耦合强度较弱的情况,而本文没有做此设定.对于叶子节点向中心节点耦合的三层及多层星形网络,我们讨论的是层内耦合强度较弱的情况和层间中心节点之间的耦合强度较弱的情况;而对于中心节点向叶子节点耦合的三层及多层星形网络的超拉普拉斯矩阵的最小非零特征值是确定的,不需要讨论.相对于文献[45]研究的两层网络,本文重点研究了多层网络,并且得出了网络的同步能力深受层数的影响.

由于多层网络复杂庞大,本文对有向网络进行了简单一般化,得到当同步域无界时,网络层数的增大使网络的同步能力增强;在同步域有界的情况下,当层间中心节点之间的耦合强度较弱时,层数对两种有向耦合方式的多层星形网络的同步能力的影响相同,而当层内耦合强度较弱时,层数对两种有向耦合方式的多层星形网络的同步能力的影响不同;对于叶子节点向中心节点单向耦合的多层星形网络,节点数的变化对网络的同步能力没有影响.由于简单一般化的网络与实际网络的复杂无规则性还有一定的差异,目前,多层网络的研究仍然还有很多问题没有解决:譬如本文的多层单向耦合的星形网络,层间在有向耦合的情况下,网络的特征值谱以及同步能力问题;对于多层星形网络,在层内耦合强度改变了网络的同步能力的情况下,如何改变其他参数来使同步能力保持不变.特征值谱方法对研究规则网络的同步能力问题有巨大的贡献,而Newman-Watts小世界网络介于最近邻耦合规则网络与全局耦合网络之间,是否可以推广到多层小世界网络的研究也有待验证.目前多层网络的理论模型在应用层面还较为薄弱,主要由于理论模型与实际数据存在一定差距,未来随着多层网络理论越来越逼近现实系统,会产生较好的应用前景.

[1]Tang L,Lu J A,Wu X,Lü J H 2013Nonlinear Dyn.73 1081

[2]Wang X F 2002Int.J.Bifur.Chaos12 885

[3]Barrat A,Barthélemy M,Vespignani A 2004Phys.Rev.Lett.92 228701

[4]Wang W X,Wang B H,Hu B,Yan G,Ou Q 2005Phys.Rev.Lett.94 188702

[5]Ide Y,Izuhara H,Machida T 2016Physics457 331

[6]Dahan M,Levi S,Luccardini C,Rostaing P,Riveau B,Triller A 2003Science302 442

[7]Raquel A B,Borgeholthoefer J,Wang N,Moreno Y,Gonzálezbailón S 2013Entropy15 4553

[8]Boukobza E,Chuchem M,Cohen D,Vardi A 2009Phys.Rev.Lett.102 180403

[9]Weber S,Hütt M T,Porto M 2008Europhys.Lett.82 28003

[10]Luan Z 2008Phys.Rep.469 93

[11]Arenas A,Díaz-Guilera A,Kurths J,Moreno Y,Zhou C 2008Phys.Reports469 93

[12]Timme M,Wolf F,Geisel T 2004Phys.Rev.Lett.92 074101

[13]Motter A E,Zhou C,Kurths J 2005Phys.Rev.E71 016116

[14]Xue M,Yeung E,Rai A,Roy S,Wan Y,Warnick S 2011Complex Syst.21 297

[15]Cai S,Zhou P,Liu Z 2014Nonlinear Dyn.76 1677

[16]Chen Y,Yu W,Tan S,Zhu H 2016Automatica70 189

[17]Boccaletti S,Latora V,Moreno Y,Chavez M,Hwang D U 2006Phys.Rep.424 175

[18]Massah S,Hollebakken R,Labrecque M P,Kolybaba A M,Beischlag T V,Prefontaine G G 2004Phys.Rev.Lett.93 218701

[19]Song Q,Cao J,Liu F 2010Phys.Lett.A374 544

[20]He P,Jing C G,Fan T,Chen C Z 2014Complexity19 10

[21]Arenas A,Díazguilera A,Pérezvicente C J 2006Phys.Rev.Lett.96 114102

[22]Zhang Q,Zhao J 2012Nonlinear Dyn.67 2519

[23]Zhang Q,Luo J,Wan L 2013Nonlinear Dyn.71 353

[24]Ling L,Li C,Wang W,Sun Y,Wang Y,Sun A 2014Nonlinear Dyn.77 1

[25]Pacheco J M,Traulsen A,Nowak M A 2006Phys.Rev.Lett.97 258103

[26]Zhang J,Small M 2006Phys.Rev.Lett.96 238701

[27]Gómez-Gardeñes J,Moreno Y,Arenas A 2007Phys.Rev.Lett.98 034101

[28]Murase Y,Török J,Jo H H,Kaski K,Kertész J 2014Phys.Rev.E90 052810

[29]Cardillo A,Zanin M,Gómez-Gardeñes J,Romance M,Amo A J G D,Boccaletti S 2013Eur.Phys.J.Special Topics215 23

[30]Bassett D S,Wymbs N F,Porter M A,Mucha P J,Carlson J M,Grafton S T 2011Proc.Nat.Acad.Sci.USA108 7641

[31]Li Y,Wu X,Lu J,Lu J 2015IEEE Trans.Circ.Syst.II Express Briefs63 206

[32]Kivelä M,Arenas A,Barthelemy M,Gleeson J P,Moreno Y,Porter M A 2014J.Complex Netw.2 203

[33]Lü J H 2008Adv.Mech.38 713(in Chinese)[吕金虎2008力学进展38 713]

[34]Lu J A 2010Complex Syst.Complex Sci.7 19(in Chinese)[陆君安2010复杂系统与复杂性科学7 19]

[35]Baptista M S,Garcia S P,Dana S K,Kurths J 2008Eur.Phys.J.Special Topics165 119

[36]Lee T H,Ju H P,Wu Z G,Lee S C,Dong H L 2012Nonlinear Dyn.70 559

[37]Qin J,Yu H J 2007Acta Phys.Sin.56 6828(in Chinese)[秦洁,于洪洁2007物理学报56 6828]

[38]Wang J,Zhang Y 2010Phys.Lett.A374 1464

[39]Zhao M,Wang B H,Jiang P Q,Zhou T 2005Prog.Phys.25 273(in Chinese)[赵明,汪秉宏,蒋品群,周涛 2005物理学进展25 273]

[40]Gómez S,Díazguilera A,Gómezgardeñes J,Pérezvicente C J,Moreno Y,Arenas A 2013Phys.Rev.Lett.110 028701

[41]Almendral J A,Díazguilera A 2007New J.Phys.9 187

[42]Granell C,Gómez S,Arenas A 2013Phys.Rev.Lett.111 128701

[43]Pecora L M,Carroll T L 1998Phys.Rev.Lett.80 2109

[44]Liang Y,Wang X Y 2012Acta Phys.Sin.61 038901(in Chinese)[梁义,王兴元 2012物理学报 61 038901]

[45]Xu M M,Lu J A,Zhou J 2016Acta Phys.Sin.65 028902(in Chinese)[徐明明,陆君安,周进 2016物理学报 65 028902]

[46]Aguirre J,Sevillaescoboza R,Gutiérrez R,Papo D,Buldú J M 2014Phys.Rev.Lett.112 248701

[47]Dabrowski A 2012Nonlinear Dyn.69 1225

[48]Johnson G A,Mar D J,Carroll T L,Pecora L M 1998Phys.Rev.Lett.80 3956

[49]Sun J,Bollt E M,Nishikawa T 2008Europhys.Lett.85 60011

[50]Xu M,Zhou J,Lu J A,Wu X 2015Euro.Phys.J.B88 240

[51]Xu W G,Wang L G 2016Acta Math.Appl.Sin.39 801

Synchronizability and eigenvalues of multilayer star networks through unidirectionally coupling∗

Sun Juan1)2)Li Xiao-Xia1)2)†Zhang Jin-Hao1)2)Shen Yu-Zhuo1)2)Li Yan-Yu1)2)

1)(State Key Laboratory of Reliability and Intelligence of Electrical Equipment,Hebei University of Technology,Tianjin 300130,China)

2)(Key Laboratory of Electromagnetic Field and Electrical Apparatus Reliability of Hebei Province,Hebei University of Technology,Tianjin 300130,China)

1 April 2017;revised manuscript

16 May 2017)

Previous studies on multilayer networks have found that properties of multilayer networks show great differences from those of the traditional complex networks.In this paper,we derive strictly the spectra of the Supra-Laplace matrix of three-layer star networks and multilayer star networks through unidirectionally coupling by using the master stability method to analyze the synchronizability of these two networks.Through mathematical analyses of the eigenvalues of the Supra-Laplace matrix,we explore how the node number,the intra-layer coupling strength the inter-layer coupling strength,and the layer number in fluence the synchronizability of multilayer star networks through unidirectionally coupling in two different ways.In particular,we focus on the layer number and the inter-layer coupling strength between the hub nodes,and then we conclude that the synchronizability of networks is greatly affected by the layer number.We f i nd that when the synchronous region is unbounded,the synchronizability of the two different coupling multilayer star networks is related to not only the intra-layer coupling strength or the inter-layer coupling strength between the leaf nodes of the entire network,but also the layer number.If the synchronous region of two different coupling multilayer star networks is bounded,and the intra-layer coupling strength is weak,the synchronizability of the two different coupling multilayer star networks is different with the changing of the intra-layer coupling strength and the inter-layer coupling strength between the leaf nodes and the layer number.If the synchronous region of two different coupling multilayer star networks is bounded,and the inter-layer coupling strength between the hub nodes is weak,the two different coupling multilayer star networks are consistent with the changing of the intra-layer coupling strength and the layer number while different from the inter-layer coupling strength between the leaf nodes and the inter-layer coupling strength between the hub nodes.We find that the node number has no effect on the synchronizability of multilayer star networks through coupling from the hub node to the leaf node.The synchronizability of the network is directly proportional to the layer number,while inversely proportional to the inter-layer coupling strength between the hub nodes.Finally,the effects of the coupling strength,the layer number and the node number on the synchronizability of the two different coupling star networks can be extended from three-layer network to multilayer networks.

*Project supported by the Natural Science Foundation of Hebei Province,China(Grant No.E2011202051).

†Corresponding author.E-mail:lixiaoxia@hebut.edu.cn

multilayer star networks,unidirectional network,eigenvalue spectrum,synchronization

PACS:89.75.Fb,89.75.Hc,89.75.–k,89.70.aDOI:10.7498/aps.66.188901

(2017年4月1日收到;2017年5月16日收到修改稿)

随着复杂网络同步的进一步发展,对复杂网络的研究重点由单层网络转向更加接近实际网络的多层有向网络.本文分别严格推导出三层、多层的单向耦合星形网络的特征值谱,并分析了耦合强度、节点数、层数对网络同步能力的影响,重点分析了层数和层间中心节点之间的耦合强度对多层单向耦合星形网络同步能力的影响,得出了层数对多层网络同步能力的影响至关重要.当同步域无界时,网络的同步能力与耦合强度、层数有关,同步能力随其增大而增强;当同步域有界时,对于叶子节点向中心节点耦合的多层星形网络,当层内耦合强度较弱时,层内耦合强度的增大会使同步能力增强,而层间叶子节点之间的耦合强度、层数的增大反而会使同步能力减弱;当层间中心节点之间的耦合强度较弱时,层间中心节点之间的耦合强度、层数的增大会使同步能力增强,层内耦合强度、层间叶子节点之间的耦合强度的增大反而会使同步能力减弱.对于中心节点向叶子节点耦合的多层星形网络,层间叶子节点之间的耦合强度、层数的增大会使同步能力增强,层内耦合强度、节点数、层间中心节点之间的耦合强度的增大反而会使同步能力减弱.

10.7498/aps.66.188901

∗河北省自然科学基金(批准号:E2011202051)资助的课题.

†通信作者.E-mail:lixiaoxia@hebut.edu.cn