加权网络中基于冗余边过滤的k-核分解排序算法∗

罗仕龙 龚凯 唐朝生 周靖

1)(西南财经大学经济信息工程学院,成都 611130)

2)(河南理工大学计算机科学与技术学院,焦作 454000)

加权网络中基于冗余边过滤的k-核分解排序算法∗

罗仕龙1)龚凯1)†唐朝生2)周靖1)

1)(西南财经大学经济信息工程学院,成都 611130)

2)(河南理工大学计算机科学与技术学院,焦作 454000)

加权网络,k-核分解,冗余边,传播影响力

1 引 言

现实社会中的许多系统都可以很自然地抽象成复杂网络[1],例如航空网络[2]、在线虚拟网络[3]、社会网络[4]等.在这些复杂网络中,鉴别重要节点的研究工作对于预防基础设施遭受攻击[5]、阻止传染病在人群中爆发[6−8]、抑制谣言信息在社会上扩散[9]等方面有着非常重要的理论意义和指导作用.一般而言,重要节点是指具有重要传播影响力的少数节点[10],通过传播途径快速地影响网络上大多数节点.因此,如何有效地度量网络节点的传播影响力既是发现重要节点的主要方法,也是复杂网络研究领域的热点问题[11,12].

近年来,复杂网络节点的核数研究引起了学者们的高度关注[13−15].核数(core)是指节点在网络上的位置核心性[16],基本思想是通过递归过程移除网络中当前度数小于或等于k值的剩余节点,剩下最大核数的节点组成网络核心层.Kitsak等[17]基于k-核分解思想(k-shell decomposition),提出用核数度量节点的传播影响力,取得了相比度数[18]和介数[19]更准确的排序结果.k-核分解法优点在于方法简单且计算复杂度低,但存在排序结果粗粒化等缺陷.国内外学者对此提出了许多改良措施[20−25],这些研究多数都是基于无权网络结构.有些学者[26−28]利用权重信息定义加权度数以替换核分解过程中的当前剩余度,提出了加权网络上的k-核排序算法.

最新实证研究发现[29],一些网络上存在局域连接稠密的特殊构型是导致k-核分解无效的根本原因之一.对此,文献[30]提出过滤某些边来减少稠密结构对k-核分解过程造成干扰的方法,指出边是否为应该过滤的冗余边(redundant links)取决于边在传播过程中具备的扩散性(diffusion im-portance),并利用边两端节点的外部连边数度量边的扩散性,但这种方法并不适用于加权网络.我们考虑到现实网络上边含有权重的普遍性,利用节点的权重特征重新定义边的扩散性,提出适用于加权网络结构的基于冗余边过滤的k-核分解排序算法: filter-core.仿真结果显示,利用节点的权重特征过滤冗余边后求得的节点核数,能够更准确地度量加权网络上重要节点的传播影响力.本文结构如下:首先提出节点权重和权重分布指数的计算方法,求出节点传播系数,根据两端节点的传播系数计算出边的扩散系数,过滤该系数低于阈值的所有网络边;接着,在剩余网络上实施k-核分解求出节点核数;最后通过世界贸易网、线虫脑细胞网和科学家合著网等真实加权网络上的SIR(susceptible-infected-recovered)传播仿真,分别与其他加权k-核分解法[26−28]的排序准确性进行比较分析.实验结果表明,本文算法能够更准确地识别加权网络上具有重要传播影响力的核心节点及核心层.

2 算法理论

最新研究证实[29],k-分解法在许多真实网络上失效的根本原因之一是这些网络中存在着局域连接稠密的微观构型,这些微观构型可以是稠密三角形,或是其他能够形成稠密回路的特殊构型.这些微观构型会导致k-分解过程把网络上局域区域连接稠密的一些节点误判为核心节点,而这些节点影响力受限于连接稠密的局部区域,并不具备重要影响力;同时,这些微观构型的稠密性也容易导致网络节点的邻居重叠程度过高,造成多源传播覆盖区域出现太多重叠,严重地制约多源传播影响力.对此,文献[30]提出一种过滤网络冗余边来减少稠密结构从而提高k-核分解准确性的方法,指出边是否应该过滤取决于该边在传播过程中具备的扩散性,例如无权网络上边两端节点的外部连边数越多,意味着传播途径越广,这条边的扩散性越强.受到上述思想的启发,我们考虑到现实网络上边含有权重的普遍性[31],提出利用节点的权重特征重新定义边的扩散性.一般地,加权网络上节点权重等于边的权重和,其大小意味着该节点对周围邻居影响程度的强弱,同时,边的权重分布特征又意味着该节点在传播过程中传播途径的多样性或局限性[32].因此,我们认为具备高权重且权重呈均匀分布特征的节点间的边,能够在传播过程中起到很重要的扩散作用.简单地说,加权网络上边的扩散性依赖于两端节点的权重,也依赖于两端节点的权重分布特征.本文用符号Iij表示边的扩散系数,Ii表示节点的传播系数,Di表示节点权重,Hi表示节点权重分布指数.这里,Iij通过计算边两端节点的传播系数Ii求出:

利用边的权重定义节点权重时,最常见的做法是按照网络边的权重均值进行归一化处理[26],但这样处理后的权重是一个绝对值.我们提出节点权重的计算公式如下:

这里wij表示边eij的实际权重.为了量化节点的权重分布特征,参考文献[33]中的度分布异质指数,本文提出权重分布指数Hi的计算式:

在附录A中,我们利用Kendall[34]相关系数τ进一步分析本文所提出的权重特征指标与节点传播影响力之间的相关性,结果表明τ(Ii)>τ(Di)>τ(Hi).

利用边过滤后实施k-核数分解的思想, filtercore算法分成过滤和分解两个阶段.首先,在过滤阶段,计算并求出原始网络上所有边的扩散系数Iij.如果该系数小于阈值θ,则视为冗余边进行过滤,直至剩余网络中所有边的系数Iij都大于阈值.这里要根据具体情况进行算法阈值θ的选取:选值过大会严重破坏网络结构,得到的核数不能代表节点在原始网络上的核心性;选值太小又无法实施有效地过滤.对此,我们遵循文献[26]中提出的过滤后网络核心层规模趋稳作为选取阈值θ的依据.接着,在核数分解阶段,移除剩余网络中当前度数等于1的所有节点,被移除后的节点处在网络的边缘核层,核数ks=1;继续移除剩余度数等于2的网络节点,核数ks=2;直至所有节点都被赋予相应的核数后,核数分解结束.此时,最大核数的节点称为网络核心节点,最大核数的核层称为网络核心层. filter-core算法在过滤阶段的计算复杂度为分解阶段[35]的计算复杂度为O(N+E),其中N表示网络节点规模数,E表示网络边数.经过数学推导可知,算法的计算复杂度为O(N+E3/2).

为了验证 filter-core算法与其他加权k-核分解法的排序优劣,本文选用三种适用于加权网络结构的k-核分解法:weighted degree方法[26]通过重新定义度数和权重的乘积关系作为k-核分解过程中使用的剩余度数(本文简称m-core),s-core算法[27]是利用节点的边权重和进行核数分解,weightedk-shell方法[28]将节点度数与权重的线性相加定义成核数分解时的剩余度数(本文简称p-core).

3 实验数据和算法应用

3.1 实验数据

本文实验数据选用三个真实加权网络:世界贸易网(ITN)[36]、线虫脑细胞网(CEL)[37]和科学家合著网(SCIE)[38],来检验 filter-core算法度量节点传播影响力的准确性.其中,ITN权重表示国家之间的贸易额,权重分布接近广延指数特征;CEL权重表示秀丽隐杆线虫的细胞数量,权重幂率系数等于1.76±0.08;SCIE权重表示科学家之间合作发表的论文数量,权重分布呈指数特征.表1统计了网络结构特征量,⟨k⟩表示平均度,l表示节点间平均最短路径,C表示聚类系数[39].可以看出,ITN表现出高聚类系数与短路径的小世界特性,又具有度数分布服从无标度的性质[40].相反,CEL聚类系数偏低且路径短,更接近随机网络结构.SCIE具有高聚类系数和路径长的双重特征,呈现规则网络的特性.上述网络表征不同的结构特征,能够更好地评估算法在真实加权网络上的有效性.

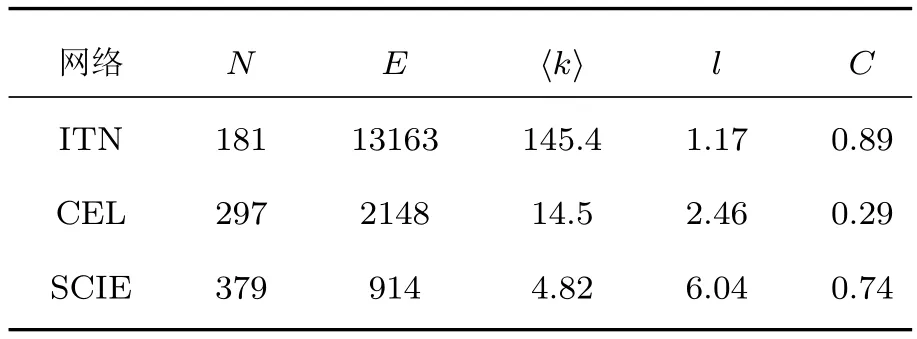
表1 网络拓扑的结构特征量Table 1.Structural properties of real weighted networks.

图1 核心层的节点规模随阈值的变化 (a)ITN;(b)CEL;(c)SCIEFig.1.Scale of the max-core for different redundant link thresholds θ in weighted networks:(a)ITN;(b)CEL;(c)SCIE.

3.2 算法实际应用

根据算法理论可知,阈值θ选取是根据过滤结束后网络核心层规模是否趋稳为依据,图1描述的是 filter-core算法应用在具体网络上的阈值选取过程.图中横坐标表示阈值θ,纵坐标表示核心层的节点规模数.由图1可见,随着阈值θ的不断增长,初期臃肿的核心层规模逐渐缩减,达到一定值时,核心层规模基本趋于稳定.例如ITN网络阈值θ=0时,核心层规模数等于152;当阈值θ>2.2时,规模数在很长一段都稳定在13附近.依据以上分析,得出θ(ITN)=2.3,θ(CEL)=2.5,θ(SCIE)=8.

为了进一步分析 filter-core算法求出的核数能够代表节点在原始网络上的核心性,图2描述了过滤阈值处的剩余网络的完整情况,图中纵坐标表示极大连通系数gcc.极大连通系数是指过滤后最大连通网络的节点规模占原始网络节点规模的比例,系数越大,说明剩余网络的结构完整性越高.观察不难发现(圆圈符号),三个网络在过滤阈值处都保持着较高的网络完整性(gcc(ITN)=1,gcc(CEL)=0.84,gcc(SCIE)=0.54).相反,如果连边扩散系数Iij是根据两端节点权重进行计算(倒三角符号),将会明显削弱剩余网络的结构完整性(gcc(ITN)=1,gcc(CEL)=0.74,gcc(SCIE)=0.05).同样,如果按照两端节点权重分布指数进行计算时(上三角符号),剩余网络结构也会受到严重破坏.经比较分析可知, filter-core算法选取阈值过滤后的剩余网络结构保持着较高的完整性,分解所得的核数能够从很大程度上代表节点在原始网络上的核心位置.

图2 (网刊彩色)过滤阈值与剩余网络完整性 (a)ITN;(b)CEL;(c)SCIEFig.2.(color online)Giant connected component gcc as the function of link filter threshold θ in weighted networks:(a)ITN;(b)CEL;(c)SCIE.

4 传播模型与指标

本文采用SIR模型[26]仿真加权网络上的传播过程.SIR模型是把节点按照健康状态划分成三类:易感态S是指当前未感染但存在感染可能性的节点,感染态I是指当前患病且具有感染能力的节点,康复态R是指已治愈且不再对传播行为产生任何影响的节点.感染节点以感染概率λ将传染病传给邻居,感染节点以康复率β(取值等于1)进行治愈并免疫.在加权网络的传播过程中,节点间的感染概率并非恒等[41].权重在传播路径上发挥着极其重要的作用,感染概率与节点同其自身邻居间的权重关系密切相关.根据文献[26],感染概率λ的计算公式如下:

参数m表征疾病感染性的强弱或者谣言迷惑性的强弱等.传播模型用符号M表示节点的传播影响力:

其中Mi(n)表示节点vi在第n次传播结束后的感染节点数,Mi表示节点vi在ntol次传播过程的感染节点平均数.本文对每个网络进行ntol=105次的独立重复实验.

图3描述了节点核数ks、节点传播影响力均值⟨M⟩和模型参数m三者间的变化关系,图中点线表示核数ks.观察可见,高核数节点的传播影响力总是大于核数居中和核数偏低的节点.也就是说,当参数m固定时,核数ks越大,节点传播影响力越强.进一步分析发现,当固定核数ks时,参数m与节点传播影响力⟨M⟩之间呈正相关.参数m取值范围有严格限制,取值太高会导致感染概率λ增大,造成任意节点都会以很高概率感染网络其他节点,无法有效地验证算法的优劣.对此,参考原模型的取值方法,得出不同网络的参数值:m(ITN)=6,m(CEL)=2,m(SCIE)=3.

基于SIR模型仿真,本文利用传播误差率ε、传播发散性σ、传播时间T和感染规模R等指标比较分析 filter-core与其他加权k-核分解法的排序准确性.传播误差率是指核数排序的结果与节点实际传播影响力排序结果的符合度[17]:

其中p代表节点比例,Mfilter-core(p)表示按照k-核算法( filter-core)进行核数降序的节点传播影响力M的均值,Meff(p)表示根据节点实际传播影响力降序的M均值.ε越小,说明排序结果的准确性越高.传播发散性σ是指核心节点的传播影响力M与核心层里所有节点的平均传播影响力的离散程度,即标准差:

其中ψ表示核心节点的集合,|ψ|表示核心节点的数量.σ越大,说明节点间的传播影响力的离散程度越高.传播时间T和感染规模R是指核心层里的核心节点作为多源传播节点,在传播时间内感染的网络节点数.在规定传播时间T内,感染规模R越大,说明整个核心层的传播影响力越强.

图3 (网刊彩色)不同核数节点的传播影响力随m值的变化趋势 (a)ITN;(b)CEL;(c)SCIEFig.3.(color online)Comparison of⟨M⟩vs.m for different cores in weighted networks:(a)ITN;(b)CEL;(c)SCIE.

5 结果分析

图4描述了核数分解排序后的节点比例p与传播误差率ε的变化,横坐标表示按照核数降序的节点比例,纵坐标表示传播误差率,圆圈符号(倒三角、方块、十字)表示采用 filter-core算法(m-core,s-core,p-core)分解得到的核数排序结果,数值ε越低,说明排序准确性越高.观察图4(a)不难发现,f i lter-core核数排序后的误差率最低;其次是s-core和p-core,这两者排序的结果几乎重叠但误差率都不低;误差率最高的是m-core分解后的核数排序.进一步观察图4(b)和图4(c)可见,我们提出的算法在CEL网络和SCIE网络上依然保持着较大优势,能够很好地度量加权网络上具有重要传播影响力的少数节点.

图4 (网刊彩色)传播误差率随节点比例的变化 (a)ITN;(b)CEL;(c)SCIEFig.4.(color online)The imprecision index ε as the function of node ratio p in weighted networks:(a)ITN;(b)CEL;(c)SCIE.

图5 (网刊彩色)核心层节点的传播发散性随m值的变化 (a)—(c)ITN;(d)—(f)CEL;(g)—(i)SCIEFig.5.(color online)Standard deviation σ of each node’s spreading in fluence for max-core vs.m in weighted networks:(a)–(c)ITN;(d)–(f)CEL;(g)–(i)SCIE.

在k-核分解法中,最大核数的节点集构成了网络核心层,而处在核心层里的所有节点应当具有近似相同的传播影响力[30].对此,进一步比较分析if lter-core算法与其他加权k-核分解法找到的核心层节点在传播发散性方面的优劣表现,如图5所示.整体而言, filter-core算法在三个网络上的传播发散值σ在大多数时候都是最低,也就是说,本文算法找到的网络核心层,其内部核心节点之间的传播影响力表现得最接近.观察图5(d)—(f)可以发现,CEL网络上的传播参数m取值偏小时, filter-core算法相比其他算法在传播发散方面的优势并没有受到影响,造成该现象的原因与网络权重和网络结构都有关:CEL网络的权重分布具有幂率分布特征,这种分布特征有利于本文算法在参数m较小时依然能够区分出具有重要扩散性的网络边,有助于提高冗余边过滤的效果.另外,k-核分解法不适用于Barabási-Albert(BA)无标度网络[20],根据表1结构特征量分析得知,CEL网络结构更接近随机网络.经上述分析可知, filter-core算法更适用于权重分布具备幂率特征且结构不具备BA无标度的加权网络.

图6描述了 filter-core算法与其他k-核分解法找到的核心层节点作为多源传播节点时,传播时间T与感染规模R之间的变化.由图6可见,ITN网络感染规模R≈80%时, filter-core算法的传播时间T=2,相反其他算法的传播时间T都大于6;在CEL网络中,当传播时间T=8时,相比score算法(m-core,p-core)感染规模R≈77%(70%,69%), filter-core算法的感染规模更高(R≈80%);在SCIE网络中, filter-core算法在传播时间T=10的感染规模R≈61%,明显强过s-core算法(mcore,p-core)在相同传播时间内的感染情况(55%,53%,37%).分析可知, filter-core找到的核心层节点在多数传播时间内的感染规模都明显高于其他k-核分解法.上述结果进一步验证了我们算法能够更准确地度量加权网络上核心节点的传播影响力.

图6 (网刊彩色)核心层节点的传播时间与感染规模之间的变化 (a)—(c)ITN;(d)—(f)CEL;(g)—(i)SCIEFig.6.(color online)Spreading time T vs.number of recovered R pro files in weighted networks:(a)–(c)ITN;(d)–(f)CEL;(g)–(i)SCIE.

6 结论与展望

真实网络上存在局域连接稠密的特殊构型是导致k-核分解结果粗粒化的本质原因之一.本文考虑到现实网络上存在权重的普遍性,利用节点权重和权重分布定义边的扩散性进而实施边过滤,提出适用于加权网络结构的基于冗余边过滤的k-核分解排序算法: filter-core.通过对世界贸易网、线虫脑细胞网和科学家合著网等真实数据的SIR传播实验表明,该算法的传播误差率相比其他加权k-核分解法的值更低,该结果表明我们算法得出的节点核数能够更准确地度量加权网络上重要节点的传播影响力;利用传播发散性、传播时间和感染规模等指标进行比较分析,结果进一步表明该算法能够更准确地识别加权网络上具有重要传播影响力的网络核心层.

本文利用权重特征和边过滤的思想对加权网络上节点的核数排序进行了研究,该工作有助于人们进一步发现复杂网络上的重要节点以提高传播效率或阻止疾病传染及谣言传播等,同时也为深入研究真实网络的核心层结构等后续工作提供了有力的支持.

感谢审稿专家对文章提出的宝贵意见和建议,这对本文研究工作的完善和提高起到了非常重要的作用.

附录A 权重特征指标与节点传播影响力之间的相关性

这里采用Kendallτ相关系数,基于真实加权网络世界贸易网(ITN)、线虫脑细胞网(CEL)和科学家合著网(SCIE),分析节点的权重特征指标传播系数Ii((2)式)、权重Di((3)式)和权重分布指数Hi((4)式)与节点的传播影响力M((6)式)之间的相关性.观察图A1可见,综合考虑权重和权重分布的节点传播系数Ii与节点传播影响力M的相关系数τ(ITN)=0.861,τ(CEL)=0.744,τ(SCIE)=0.371,明显高于节点权重Di与传播影响力M之间的相关系数τ(ITN)=0.738,τ(CEL)=0.648,τ(SCIE)=0.221,也明显高于权重分布指数的相关系数τ(ITN)=0.531,τ(CEL)=0.597,τ(SCIE)=0.103. 结果表明,加权网络上利用节点权重和权重分布能够更准确地反映出节点在传播中的重要性,也进一步说明利用边两端节点的传播系数Ii可以更有效地度量边在传播过程中发挥的扩散作用.

图A1节点的权重特征指标与传播影响力之间的相关性 (a)—(c)ITN;(d)—(f)CEL;(g)—(i)SCIEFig.A1.M vs.measuring index pro files in weighted networks:(a)–(c)ITN;(d)–(f)CEL;(g)–(i)SCIE.

[1]Wang X F,Li X,Chen G R 2012Network Science:an Introduction(Beijing:Higher Education Press)pp3–18(in Chinese)[汪小帆,李翔,陈关荣2012网络科学导论(北京:高等教育出版社)第3—18页]

[2]Liu H K,Zhou T 2007Acta Phys.Sin.56 106(in Chinese)[刘宏鲲,周涛 2007物理学报 56 106]

[3]Zhang Z K,Liu C,Zhan X X,Lu X,Zhang C X,Zhang Y C 2016Phys.Rep.651 1

[4]Liu C,Zhan X X,Zhang Z K,Sun G Q,Hui P M 2015New J.Phys.17 113045

[5]Cohen R,Erez K,Benavraham D,Havlin S 2001Phys.Rev.Lett.86 3682

[6]Liu J G,Lin J H,Guo Q,Zhou T 2016Sci.Rep.6 21380

[7]Keeling M J,Rohani P 2008Modeling Infectious Diseases in Humans and Animals(Princeton:Princeton University Press)p366

[8]Gong K,Tang M,Hui P M,Zhang H F,Younghae D,Lai Y C 2013Plos One8 e83489

[9]Liu C,Zhang Z K 2014Commun.Nonlinear Sci.19 896

[10]Crucitti P,Latora V,Marchiori M,Rapisarda A 2004Physica A340 388

[11]Liu J G,Ren Z M,Guo Q,Wang B H 2013Acta Phys.Sin.62 178901(in Chinese)[刘建国,任卓明,郭强,汪秉宏2013物理学报62 178901]

[12]Ren X L,Lü L Y 2014Chin.Sci.Bull.59 1175(in Chinese)[任晓龙,吕琳媛 2014科学通报 59 1175]

[13]Rombach M P,Porter M A,Fowler J H,Mucha P J 2014Siam J.Appl.Math.74 167

[14]Bassett D S,Wymbs N F,Rombach M P,Porter M A,Mucha P J,Grafton S T 2013Plos Comput.Biol.9 e1003171

[15]Liu J G,Ren Z M,Guo Q,Chen D B 2014Plos One9 e104028

[16]Seidman S B 1983Social Networks5 269

[17]Kitsak M,Gallos L K,Havlin S,Liljeros F,Muchnik L,Stanley H E,Makse H A 2010Nat.Phys.6 888

[18]Chen D,Lü L,Shang M S,Zhang Y C,Zhou T 2012Physica A391 1777

[19]Freeman L 1977Sociometry40 35

[20]Zeng A,Zhang C J 2013Phys.Lett.A377 1031

[21]Hou B,Yao Y,Liao D 2012Physica A391 4012

[22]Liu J G,Ren Z M,Guo Q 2013Physica A392 4154

[23]Hu Q C,Yin Y S,Ma P F,Gao Y,Zhang Y,Xing C X 2013Acta Phys.Sin.62 140101(in Chinese)[胡庆成,尹龑燊,马鹏斐,高旸,张勇,邢春晓2013物理学报62 140101]

[24]Ren Z M,Liu J G,Shao F,Hu Z L,Guo Q 2013Acta Phys.Sin.62 108902(in Chinese)[任卓明,刘建国,邵凤,胡兆龙,郭强2013物理学报62 108902]

[25]Cao J X,Dong D,Xu S,Zheng X,Liu B,Luo J Z 2015Chin.J.Comput.38 238(in Chinese)[曹玖新,董丹,徐顺,郑啸,刘波,罗军舟2015计算机学报38 238]

[26]Garas A,Schweitzer F,Havlin S 2012New J.Phys.14 83030

[27]Eidsaa M,Almaas E 2013Phys.Rev.E88 062819

[28]Wei B,Liu J,Wei D,Gao C,Deng Y 2015Physica A420 277

[29]Liu Y,Tang M,Zhou T,Do Y 2015Sci.Rep.5 9602

[30]Liu Y,Tang M,Zhou T,Do Y 2015Sci.Rep.5 13172

[31]Barrat A,Barthélemy M,Pastor-Satorras R,Vespignani A 2004Proc.Natl.Acad.Sci.USA101 3747

[32]Yan W,Zhou T,Wang J,Fu Z Q,Wang B H 2005Chin.Phys.Lett.22 510

[33]Hu H B,Wang X F 2008Physica A387 3769

[34]Kendall M G 1938Biometrika30 81

[35]Batagelj V,Zaversnik M 2003 arXiv:cs/0310049v1

[36]Lee K M,Yang J S,Kim G,Lee J,Goh K I,Kim I M 2011Plos One6 e18443

[37]Watts D J,Strogatz S H 1998Nature393 440

[38]Newman M E J 2006Phys.Rev.E74 036104

[39]Saramäki J,Kivelä M,Onnela J P,Kaski K,Kertész J 2007Phys.Rev.E75 027105

[40]Li X,Jin Y Y,Chen G R 2003Physica A328 287

[41]Yan G,Fu Z Q,Chen G 2008Eur.Phys.J.B65 591

A ranking approach based onk-shell decomposition method by filtering out redundant link in weighted networks∗

Luo Shi-Long1)Gong Kai1)†Tang Chao-Sheng2)Zhou Jing1)

1)(School of Economic Information Engineering,Southwestern University of Finance and Economics,Chengdu 611130,China)

2)(School of Computer Science and Technology,Henan Polytechnic University,Jiaozuo 454000,China)

16 December 2016;revised manuscript

21 June 2017)

Thek-shell decomposition method of identifying the in fluential nodes which accelerate spread or hinder propagation,plays an important role in analyzing the spreading performance of complex network,but it is too coarse in terms of ranking granularity.Recent study shows that the accuracy of thek-shell decomposition method in determining node coreness is significantly affected by the mutually densely connected local structures.Existing approach tries to filter out the confusion of the classicalk-shell decomposition method,caused by such densely local structures,through rede fining a diffusion importance value which is the number of out-leaving links at/from the nodes connected by a link.This value is used to quantify the potential in fluence of a link in spreading process.However,the existing approach is not suitable for ubiquitously weighted networks.In this paper,we develop a new ranking approach( filter-core)to identify the node spreading in fluence in weighted network.Here,we concern that the redundant links,although they are less important in the spreading process,form mutually densely connected local structures,which lead to the classicalk-shell decomposition method unable to accurately determine the coreness of node in network.By rede fining a new diffusion importance value for each link based on the weights of its connected nodes and the weight distribution,we filter out the redundant links which have a relatively low diffusion importance in the spreading process.After filtering out all redundant links and applying the classicalk-shell decomposition method to the residual network,we obtain a new coreness for each node,which is more accurate to indicate spreading in fluence of node in the original network.Our approach is applied to three real weighted networks,i.e.,the international trading network,the neural network of C.elegans,and the coauthorship network of scientists.And the susceptible-infected-recovered epidemic spreading model is used to make a comparison of performance between our approach and other threek-shell methods(including the weighted degree decomposition method,the s-core decomposition method,and the weightedk-shell method)in terms of four quantitative indices,i.e.,the imprecision function,the standard deviation of infected fraction of max coreness node,the spreading time,and the number of recovered nodes at the end of spreading process.The experimental results show that our proposed approach is more accurate to identify the in fluential spreaders than the weighted degree decomposition method,the score decomposition method,and the weightedk-shell method,and also helps to more accurately decompose the network core structure for an optimal analysis in weighted network.

weighted networks,k-shell decomposition,redundant link,spreading in fluence

PACS:89.75.–k,89.75.Fb,05.10.–aDOI:10.7498/aps.66.188902

*Project supported by the National Natural Science Foundation of China(Grant No.61602331),the Fundamental Research Funds for the Central Universities of Ministry of Education of China(Grant Nos.JBK170133,JBK160130,JBK150503),the Scientific Research Foundation of the Education Department of Sichuan Province,China(Grant No.17ZB0434),and the Collaborative Innovation Center for Electronic Finance and Financial Regulation.

†Corresponding author.E-mail:gongkai1210@swufe.edu.cn

(2016年12月16日收到;2017年6月21日收到修改稿)

k-核分解排序法对于度量复杂网络上重要节点的传播影响力具有重要的理论意义和应用价值,但其排序粗粒化的缺陷也不容忽视.最新研究发现,一些真实网络中存在局域连接稠密的特殊构型是导致上述问题的根本原因之一.当前的解决方法是利用边两端节点的外部连边数度量边的扩散性,采取过滤网络边来减少这种稠密结构给k-核分解过程造成的干扰,但这种方法并没有考虑现实网络上存在权重的普遍性.本文利用节点权重和权重分布重新定义边的扩散性,提出适用于加权网络结构的基于冗余边过滤的k-核分解排序算法: filter-core.通过世界贸易网、线虫脑细胞网和科学家合著网等真实网络的SIR(susceptible-infectedrecovered)传播模型的仿真结果表明,该算法相比其他加权k-核分解法,能够更准确地度量加权网络上具有重要传播影响力的核心节点及核心层.

10.7498/aps.66.188902

∗国家自然科学基金(批准号:61602331)、中央高校基本科研业务费专项资金(批准号:JBK170133,JBK160130,JBK150503)、四川省教育厅科研基金(批准号:J17ZB0434)和互联网金融创新及监管协同创新中心资助的课题.

†通信作者.E-mail:gongkai1210@swufe.edu.cn