一种基于单水听器的浅海水下声源被动测距方法∗

李晓曼 朴胜春2) 张明辉2) 刘亚琴 周建波

1)(哈尔滨工程大学水声工程学院,哈尔滨 150001)

2)(哈尔滨工程大学,水声技术重点实验室,哈尔滨 150001)

一种基于单水听器的浅海水下声源被动测距方法∗

李晓曼1)朴胜春1)2)张明辉1)2)†刘亚琴1)周建波1)

1)(哈尔滨工程大学水声工程学院,哈尔滨 150001)

2)(哈尔滨工程大学,水声技术重点实验室,哈尔滨 150001)

海底相移参数,warping变换,群延迟,被动测距

1 引 言

宽带信号在浅海波导中传播时,接收信号由各阶简正波之间相互干涉叠加而成,每阶简正波都保留了大量的海洋环境信息,如何有效地利用各阶简正波的信息进行水下声源的定位是近年来水声领域的一个重要研究内容[1],而基于单水听器的水下声源的被动测距则是其中的一个重要方面.与匹配场[2]等被动测距技术不同,单水听器测距方法不需要庞大的水听器阵以及大量的声场计算,但是为了准确有效地测量声源距离,需要知道详细的波导环境参数,这为实际测量带来了困难.针对这一情况,已提出了基于波导不变量的被动测距方法和基于阵不变量的被动测距方法.基于波导不变量的被动测距方法是利用了浅海波导中声场在距离和频率的内在关系及其干涉结构特征[3],但是干涉结构的稳定性随着距离的变化而变化,所以此方法对声场距离具有依赖性.基于阵不变量的被动测距方法[4]则利用的是波导的多途效应和频散效应,对于远距离声源测距精度具有较大限制.Warping变换是近年来应用于水声领域的信号处理方法,它适用于浅海波导中宽带脉冲信号的简正波分离[5],被广泛应用于水下被动测距、海洋环境参数反演等水声研究领域[6−10].国内外学者对warping变换在水下声源单水听器被动测距方面的应用进行了广泛的研究.Zhou等[11]和王冬等[12]分别对接收信号的自相关信号和能量谱信号进行warping变换,利用处理后信号的频谱中特征频率的不变性实现对声源的测距.戚聿波等[13]理论分析了海底地形水平缓变浅海波导中warping变换时的低频声场特征频率,实现了水平变化浅海波导中声源距离的被动估计.Bonnel等[14,15]提出了两种基于warping变换的单水听器的被动测距方法,实现了简正波在时频域上的分离.第一种方法计算量小但在对距离进行反演时需要已知大量准确的海洋环境参数,第二种方法虽然只需要声场的声速剖面和深度即可对水下声源进行有效定位,对距离的宽容性较好,但需要对接收信号进行人工处理,计算量较大.群延迟是简正波频散特性的解释和应用,包含了各阶简正波之间的关系,即不同频率下同一阶简正波到达水听器的时刻不同,同样地,同一频率下不同阶简正波的到达时刻也不同[16].

本文通过将warping变换与群延迟理论相结合,提出了一种基于单水听器的水下声源的被动测距方法.利用warping变换对其各阶简正波模态进行分离和提取,对得到的单阶简正波信号进行时频分析处理可以对各阶简正波频散曲线进行提取,从而得到任意两阶简正波的时延差.根据群延迟理论,已知任意两阶简正波的时延差和群慢差可以对声源位置进行被动测距.在海洋环境参数已知的情况下可以利用声学计算软件计算不同阶简正波的群慢差,从而实现对水下声源的被动测距.在海底参数未知的情况下,海底相移参数P是描述海底地声参数的一个重要参量,包含了海底地声参数信息.当声波以小掠射角传播时,简正波类型主要是海面和海底反射(SRBR)类的简正波,这类简正波的水平波数差可以用含有海底相移参数P、海深以及海水中平均声速近似表示,根据群慢差和水平波数差之间的关系,可以求得任意两阶简正波的群慢差.本文提出的方法测量简单、计算方便.理论数值仿真误差在3%以内,两次海上实验数据处理结果的测距误差都在10%以内,证明了该方法的有效性.

本文的内容主要分为以下六部分:第2部分主要是理论描述,介绍了群延迟的基本理论,利用warping变换对简正波进行分离提取的原理,基于海底相移参数的群速度计算以及测距的基本原理;第3部分为理论仿真部分,仿真了同一环境下不同距离处对脉冲声源的测距,并将其与KRAKEN得到的测距结果进行了对比,同时对非均匀水体波导下测距方法的性能进行了分析;第4部分为实验数据处理及其结果验证,包括线性调频脉冲信号和爆炸声信号的处理;第5部分为误差分析;最后为结论.

2 理论描述

2.1 群延迟基本理论

基于简正波理论,浅海波导下位于深度zs处的接收声场信号可表示成[17]

其中,C为常数,S(f)为发射信号的频谱,Un为深度函数,ξn为水平波数,r为传播距离.

各阶群速度与简正波的阶数和频率有关,其中第n阶简正波的群速度可以表示为

对于给定的传播距离r,不同频率下同一号简正波到达水听器的时间差为[16]

而同一频率时,不同号数简正波的到达水听器时间差∆Tmn(f)可表示成

由群延迟理论可知,如果得到了不同阶简正波在同一频率下的到达水听器的时间差以及其群慢差值,就可以估算出在这一频率下单频信号的传播距离.为了得到任意两阶简正波到达的时延差,本文利用warping变换以及信号的时频分析技术提取任意阶简正波的频散曲线,得到了其关于时间与频率的关系.

2.2 Warping变换与简正波的分离

Warping变换是近年来被广泛应用的简正波模态分离技术,它是一种酉变换,适用于浅海波导且能够对单水听器的接收信号实现准确有效的分离[18].其基本理论如下[19,20].

根据简正波理论,海洋理想波导中水听器接收到的声压信号的时域表达式可以表示为

其中,tr=r/c,c为波导中的平均声速,Bn(t)为第n阶简正波的瞬时幅度,fcn是第n阶简正波的截止频率.

Warping算子h(t)表示为

将warping算子及(1)式代入warping变换的计算公式可得到warping变换的结果,

对warping变换后的信号进行简正波分离和频域滤波后,可得到单独的某阶简正波的信息,对其做warping逆变换,获得该阶简正波原始时域信号Warping变换的逆变换算子为

Warping逆变换可以表示为下式:

2.3 基于时频分析的时延差计算

在得到各阶简正波还原后的信号后,利用时频分析的处理方法可以得到各阶简正波在各个频点下到达接收水听器的时间.根据时频分析的基本原理,接收信号的时频分析(短时傅里叶变换)表达式为[10]

其中te(f)为声源在频率f下的发射时间,与声源位置和收发距离有关;Cn代表各阶简正波的幅度的衰减项.将分离后的简正波信号代入(10)式,则第n阶简正波在频率f下的到达时间为

则任意两阶简正波的时延差可以表示为

由(12)式可以看出,在求解两阶简正波的到达时延时,消除了声源和收发距离的影响,可以估算出不同阶简正波的频散曲线,得到各阶简正波关于时间和频率的关系.

为了验证计算时延差理论的有效性,对上述过程进行了仿真,仿真环境为Pekeris波导,发射声源是带宽为200—600 Hz的线性调频脉冲信号.接收信号经过warping变换处理分析后,提取前5阶简正波并将得到的各阶简正波进行时频分析,提取得到了各阶简正波的频散曲线.将计算结果与通过KRAKEN计算得到的理论值进行了比对,结果如图1所示.

图1 (网刊彩色)简正波频散曲线提取值与理论值对比Fig.1.(color online)The comparison of extracted dispersion results and the theoretical results.

由图1可以看出,低阶简正波估计值与理论值符合较好,高阶简正波在高频符合较好,高阶简正波在低频符合度较差的原因主要是在低频段低阶简正波起主要作用,高阶简正波相较于低阶简正波能量较低,在warping变换后进行滤波时,高阶简正波的能量会发生泄露,造成最终计算结果的偏差.

2.4 基于海底相移参数的群速度计算

根据群延迟理论,要实现对声源的被动测距,还需要计算任意两阶简正波的群慢差.

在已知海深和波导中的声速后,如果海底参数已知,则任意两阶简正波的群慢差可以利用声场计算软件计算得到.在海底参数未知而海底相移参数已知的情况下,对于具有液态半无限空间海底的波导,利用已知海底相移参数可以求得任意两阶简正波的水平波数差,从而求得两阶简正波的群慢差.具体推导过程如下.

水平波数的值由频散方程决定,具有液态半无限海底的波导的简正波类型主要是SRBR类简正波,考虑小入射角的情况,在Wenzel-Kramers-Brillouin近似下,该类波导的频散方程可以写为[22]

其中ξn为第n阶简正波的水平波数;b为海底反射相移,在θ≪1(即小入射角)的情况下,有

将(14)式代入(13)式可得

θn为第n阶简正波的入射角,因为考虑的是小入射角的情况,所以有θn≈sinθn,则(15)式可以简化为

引入有效深度的概念,则(16)式可以简化为

其中H为海水深度,∆H为有效深度,在不考虑剪切波的情况下,有效深度可以表示为[22]

有效深度和海底相移参数两者之间的关系如下[11]:

假定(13)式中k(z)为随深度变化的波数,假设海水中的声速剖面为[12]

其中,a(z)为声速随深度的变化量,¯c为海水中的平均声速,则有

所以有

可以得到海水中波数与水平波数的关系:

将(17)式的左侧进行泰勒级数展开并保留第一项后,(17)式可以化简为

则水平波数可以表示为[22]

则两阶简正波的水平波数差可以表示为

将(19)式代入(26)式,可以得到[23]

所以,任意两阶简正波的群慢差为

因此,在已知海深、海底相移参数以及海水中平均声速时可以直接近似计算任意两阶简正波的群慢差,相对于利用声学计算软件计算得到的结果,准确性有所降低,但不需要详细的海底环境参数,计算方便.

上述计算简正波群慢差的方法是基于海底相移参数P为常数这个假定,P为常数这个结论一般情况下只适用于均匀半无限海底,在分层海底的条件下,海底相移参数是一个随着频率变化的量.但经过研究发现,对于高声速海底,当沉积层厚度较大时,在小掠射角条件下P随频率的变化趋于稳定.本文提出的计算群慢差的方法依旧适用,但不可避免地存在计算误差.对于低声速海底,P随频率变化剧烈,本文提出的方法不再适用.因此,在海底环境参数已知的情况下,应当首先考虑利用声学计算软件计算简正波之间的群慢差,依次来减少计算误差.

2.5 测距基本原理

将(12)和(28)式代入(4)式,可以得到水下脉冲声源的被动测距公式:

对于宽带信号而言,最终距离r的确定由带宽内的多个频率点共同决定,在各个频点下得到的结果进行平均,得到平均估计距离值¯r,则¯r为被动估计的声源传播距离,

(30)式给出了水下声源被动测距的理论公式,接下来分别用数值仿真和海上实验数据来验证该理论的准确性.

3 理论仿真结果

3.1 测距方法的理论仿真

本文模拟了理想波导的海洋环境,分别利用KRAKEN声场计算软件和(28)式计算了任意两阶简正波的群慢差,并根据(30)式对声源的距离进行了仿真.

图2 (网刊彩色)分离后的两阶简正波的时频分析结果Fig.2.(color online)The time and frequency results of the separated normal modes signals.

仿真声场环境为Pekeris波导,海深H=24.5 m,声源深度zs=10 m,水听器接收深度为zr=9 m,海水的平均声速c=1500 m/s.发射一个线性调频长脉冲信号,初始频率f1=200 Hz,末频率为f2=600 Hz,带宽为f1—f2,中心频率f0=400 Hz,信号长度为10 s.仿真距离依次为5,10,15,20,25 km.根据(10)式对信号进行处理分析,可以得到图2和图3的结果,图2给出了前两阶简正波在各个频点下对应的时频分析结果,图3为经过分析计算后的各个频点下的测距结果.

图3 (网刊彩色)利用(a)KRAKEN和(b)(29)式得到的测距结果Fig.3.(color online)The estimation results in different ranges:(a)The results obtained by KRAKEN;(b)the results obtained by Eq.(29).

表1 不同距离下的测距最终结果Table 1.The last estimation results in different ranges.

由图3可以看出,低频和高频附近的结果离散性大,这主要有两方面的原因.首先由于低频尤其是在截止频率附近的群速度起伏较大,而在高频部分两阶简正波的群速度均趋近于海水中的声速,几乎不再变化,因此这两部分的值与真实值之间存在较大误差.其次在利用warping变换以及时频分析工具对信号进行分离和恢复时,在频带两端(即起始频率和最终频率)附近的处理存在不可避免的误差,使得这两部分频点的测量值与真实值之间存在差距.

为了确定最终的测量结果,通常选取图中比较稳定的频点区域进行计算,在简正波能够被激发(大于简正波的截止频率)的情况下,频段为[f0/5,4f0/5].由图3可以看出,在200—600 Hz的频带范围内,300—500 Hz范围内的结果比较稳定.根据(12)式,则有f1=300 Hz和f2=500 Hz,将f1和f2代入,可以得到各个传播距离下的最终测距结果,为利用KRAKEN得到的测量结果,而为根据(30)式得到的测量结果.由表1的结果可以看出测量误差均小于±2%,测量于±3%,结果准确.

3.2 非均匀水体波导测距方法的性能分析

对于非均匀水体波导,本文提出的测距方法包括两方面的近似:一方面,传统warping变换的形式是基于理想波导,对于非均匀水体波导不一定完全适用;另一方面,在利用海底相移参数求两阶简正波之间的群慢差时用波导的平均声速代替了波导水中声速.为了评估“warping变换”和“平均声速剖面”两方面近似对非均匀水体波导测距性能的影响,本文对含有跃层的波导进行了仿真.仿真环境中含跃层波导的声速剖面如图4所示,海深H=25 m,海底声速约为cb1=1700 m/s,海底密度为ρb1=1.5 g/cm3,海底相移参数P=6.375,收发距离r的取值范围为5—25 km.Pekeris波导海水中声速c0=1500 m/s,其余环境参数与上述波导一致.具体仿真内容包括:1)在含跃层波导下,对利用warping变换分离后提取的各阶简正波(前两阶)的频散曲线与理论上单阶简正波的直接提取结果进行了对比,结果如图5所示;2)分别在Pekeris波导和含跃层波导下,利用平均声速剖面和海底相移参数获得的不同阶简正波之间的群慢差和理论计算结果的对比,结果如图6和图7所示.

图4 含跃层波导声速剖面Fig.4.The sound speed pro file of waveguide with thermocline.

由图5仿真结果可知,对于水体含跃层的波导,利用warping变换对各阶简正波分离后提取的频散曲线与理论上单阶简正波的直接提取结果相比,一致性较强,主要原因是warping变换是一个可逆变换,在本文中warping变换作为一种分离简正波的工具,在分离简正波后还要利用warping逆变换进行还原,处理分析的为还原后的信号,对warping变换的分离精度要求相对不高.因此,在传统warping变换可以实现对接收信号的各阶简正波进行分离的情况下,对本文提出的测距方法是适用的.

根据图7所示的仿真结果,对于含跃层的波导,采用本文提出的利用海底相移参数和海水中平均声速计算得到的不同阶简正波的群速度,与在已知声速剖面的情况下利用声学软件计算得到的不同阶简正波的群速度相比存在一定的误差,低阶简正波的一致性较好,但两者之间的符合性与Pekeris波导下的结果相比,后者的一致性更高,前者计算结果的误差也是导致最终测距结果误差的主要原因之一.

图5 (网刊彩色)含跃层波导下频散曲线提取对比Fig.5.(color online)The comparison of the extracted dispersion results in waveguide with thermocline.

图6 (网刊彩色)Pekeris波导下的仿真结果 (a)群速度计算结果;(b)前两阶简正波的群慢差计算结果Fig.6.(color online)The simulation results in Pekeris waveguide:(a)The results of group speed;(b)the results of slow group speed difference of the first two orders.

图7 (网刊彩色)含跃层波导下的仿真结果 (a)群速度计算结果;(b)前两阶简正波的群慢差计算结果Fig.7.(color online)The simulation results in waveguide with thermocline:(a)The results of group speed;(b)the results of slow group speed difference of the first two orders.

因此,本文提出的计算群慢差的方法对于理想波导和Pekeris波导均适用;而对于存在跃层的浅海波导,在声速剖面以及海地环境参数均已知的情况下,利用声学计算软件计算简正波之间的群慢差是最优选择,在海底环境参数未知但海底相移参数已知的情况下,在误差允许范围内,利用本文提出方法可以快速计算不同阶简正波间的群慢差,实现对水下声源的被动测距.

4 实验数据处理

为了对本文提出的方法进行验证,分别对两次海上实验的数据进行了处理.实验数据由两次海上实验测得,一次为利用信号源发射的线性调频信号,一次为爆炸声信号.

4.1 线性调频信号数据处理

本次实验于2014年10月在黄海某海域进行,海水的平均声速¯c1约为1497 m/s,海深约为25 m,海底为半无限高声速海底,声速约为cb1=1700 m/s,海底密度为ρb1=1.5 g/cm3;使用单水听器进行信号接收,水听器接收深度zr=19 m;利用信号源发射线性调频信号,带宽为200—600 Hz,中心频率f0=400 Hz.海底相移参数P=6.375,实验中声源的实际传播距离由全球定位系统(GPS)测得r0=5.0112 km.图8为实验时的声速剖面和滤波后的接收到的时域信号,warping变换对脉冲压缩后的信号同样适用,为了方便数据处理,可对接收信号进行脉冲压缩.

图8 对于线性调频信号,(a)实验时的声速剖面和(b)接收时域信号Fig.8.For the linear frequency modulation impulse source signal,(a)the sound speed pro file of experiment and(b)the received signal in time domain.

图9给出了利用时频分析提取的各阶简正波到达接收水听器的时间与接收信号的时频分析对比,图10给出了前两阶简正波单阶简正波时频分析结果及其频散曲线提取结果.由图10可以看出,提取时间和时频分析结果符合较好,提取时间准确有效,可以用来进行时间差计算.

根据(12)式计算得到任意两阶简正波的时延,分别利用KRAKEN声场计算软件和(28)式计算了任意两阶简正波的群慢差,并根据(29)式对声源的距离进行了估计,测距结果如图11所示.

通过处理后,由KRAKEN软件计算得到群慢差时的测距结果为r′1=5.085 km,误差为1.477%;由(28)式得到群慢差时相应的测距结果为r′2=4.819 km,误差为−3.831%.上述结果误差均小于5%,证明了测距结果准确有效,说明本文提出的测距方法的有效性.

图9 (网刊彩色)对于线性调频信号,接收信号时频分析与提取时间对比Fig.9.(color online)For the linear frequency modulation impulse source signal,the comparison between the time-frequency analysis of received signal and the extractive time.

图10 (网刊彩色)对于线性调频信号,前两阶简正波时频分析及其频散曲线提取结果Fig.10.(color online)For the linear frequency modulation impulse source signal,the time frequency analysis and extracted dispersion results of the first two normal modes of received signal.

图11 对于线性调频信号,利用(a)KRAKEN和(b)(29)式得到的测距结果Fig.11.For the linear frequency modulation impulse source signal,(a)the range results by KRAKEN and(b)the range results by Eq.(29).

4.2 爆炸声数据处理

本次实验于2012年7月在大连附近某海域进行,海水的平均声速¯c约为1518 m/s,海深H=19.2 m,海底类型为高声速半无限海底,声速约为cb2=1600 m/s,海底密度为ρb2=1.5 g/cm3,海底衰减α2=0.03 dB/λ.在8个不同距离处投弹,前七个投弹点每次投弹三枚,最后一个投弹点投弹一枚,共22组数据.使用8元垂直阵水听器对信号进行接收,本次只处理其中一个水听器的接收数据,水听器接收深度zr=18 m,爆炸声处理频段为10—200 Hz.已知海底相移参数P=6.664.图12给出了该海域中海水的声速剖面及其第一枚炸弹的接收时域信号.

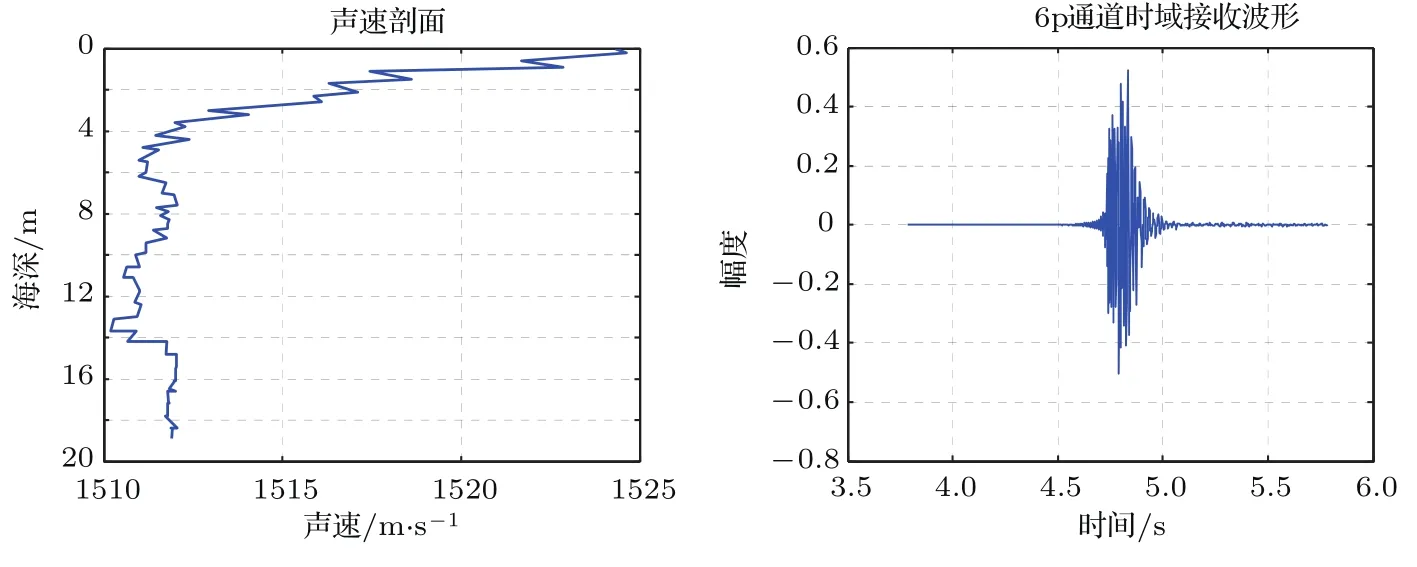
图12 对于爆炸声信号,实验时的声速剖面和接收时域信号Fig.12.For the explosion sound source signal,the sound speed pro file of experiment and the received signal in time domain.

图13 (网刊彩色)对于爆炸声信号,接收信号时频分析与提取时间对比Fig.13.(color online)For the explosion sound source signal,the comparison between the time-frequency analysis of received signal and the extractive time.

对第一枚炸弹接收信号进行处理,提取各阶简正波的频散曲线,其时频分析与提取时间的对比如图13所示,利用(29)式得到的测距结果如图14所示.

图14 对于爆炸声信号,所得到的测距结果Fig.14.The range results for the explosion sound source signal.

图15 (网刊彩色)对于爆炸声信号,所获得的测距结果和测距误差Fig.15.(color online)The range results and error for the explosion sound source signal.

按照本文提出的方法对余下的24枚弹进行了处理,并利用(30)式对声源距离进行估计,并将测距结果与GPS结果进行了对比,测距结果和测距误差如图15所示.

由测量结果可以看出,根据(30)式得到的测距结果与GPS结果相比,测距结果误差都在10%以内,测距结果可靠有效,证明了本文提出方法的准确性.

5 误差分析

本文提出的测距方法误差主要包括计算误差和测量误差两个方面.减少测量误差需要使用更加精密的仪器设备,而计算误差则包括对于不同阶简正波之间时延差的计算误差和不同阶简正波之间群慢差的计算误差.

不同阶简正波之间时延差的计算与波导的频散特性有关,通过warping变换对各阶简正波的频散曲线进行提取,得到各阶简正波时间和频率之间的关系,从而计算不同阶简正波到达水听器的时延差.而在对简正波频散曲线的提取过程中,因为简正波之间的干涉和能量泄露等原因,简正波部分频段的频散曲线不能完整且准确地提取,如图1所示.为了减少计算误差,在测距时要根据提取频散曲线的情况合理选择测距频段.一般情况下选择低阶简正波的中间部分频段可以较好地避免测距误差,频段大约为其中f0为中心频率.例如文中第3部分,接收信号带宽为200—600 Hz,进行测距时,利用前两阶简正波计算时延差,而选择的测距频段为300—500 Hz,在这个频段内频散曲线相对光滑准确.

群慢差的计算误差大小因波导的海洋环境的不同而不同.对于均匀波导(水体中声速接近等速),无论海底环境参数是否已知,群慢差的计算误差较小,利用(30)式得到的结果和利用KRAKEN得到的计算结果基本一致,仿真结果见图6.而对于非均匀波导(水体中声速非均匀),与在已知声速剖面的情况下利用声学软件计算得到的不同阶简正波的群速度相比存在一定的误差,仿真结果见图7,在这种情况下群慢差的计算结果的误差是导致最终测距结果误差的主要原因之一.

6 结 论

宽带脉冲声源在浅海波导中传播时具有明显的频散特性,接收信号为各阶简正波的干涉叠加,利用warping变换可以实现对接收信号各阶简正波的分离和提取,对单阶简正波信号进行时频分析处理可以提取各阶简正波的频散曲线,得到各阶简正波时间和频率间的关系,从而得到任意两阶简正波到达水听器的时延差.根据群延迟理论,已知任意两阶简正波的时延差和群慢差可以对声源位置进行被动测距.在海洋环境参数已知的情况下可以利用声学计算软件计算不同阶简正波的群慢差,从而实现对水下声源的被动测距.在海底参数未知的情况下,海底相移参数P是描述海底地声参数的一个重要参量,它包含了海底地声参数信息.当声波以小掠射角传播时,简正波类型主要是SRBR类的简正波,这类简正波的水平波数差可以用含有海底相移参数P、海深以及海水中平均声速近似表示.根据简正波群慢差和水平波数差之间的关系,可以求得任意两阶简正波的群慢差,通过建立相应的代价函数,可以实现利用单水听器对声源位置的被动估计.本文提出的获取时延的方法和计算群慢差的方法计算简单快速,具有较强的实用意义.通过仿真和实验数据对本文提出的方法进行了验证,测距结果与实际距离相比,符合良好,测距误差均未超过10%,充分证明了测距方法准确有效.

[1]Li Q Q 2016Chin.Phys.Lett.33 034301

[2]Li Q Q,Li Z L,Zhang R H 2013Chin.Phys.Lett.30 024301

[3]Hassab J 1983IEEE J.Oceanic Eng.8 136

[4]Zhao Z D,Wang N,Gao D Z,Wang H Z 2010Chin.Phys.Lett.27 064301

[5]Bonnel J,Chapman N R 2011J.Acoust.Soc.Am.130 101

[6]Brown J C,Hodgins D A,Miller P J O 2006J.Acoust.Soc.Am.119 EL34

[7]Ioana C,Quinquis A,Stephan Y 2006IEEE J.Oceanic Eng.31 628

[8]Bonnel J,Dosso S E,Chapman R N 2013J.Acoust.Soc.Am.134 120

[9]Zeng J,Chapman N R,Bonnel J 2013J.Acoust.Soc.Am.134 394

[10]Lin Y T,Newhall A E,Lynch J F 2012J.Acoust.Soc.Am.131 1798

[11]Zhou S H,Qi Y B,Ren Y 2014Sci.China:Phys.Mech.Astron.57 225

[12]Wang D,Guo L H,Liu J J,Qi Y B 2016Acta Phys.Sin.65 104302(in Chinese)[王冬,郭良浩,刘建军,戚聿波2016物理学报65 104302]

[13]Qi Y B,Zhou S H,Zhang R H,Zhang B,Zhang Y 2014Acta Phys.Sin.63 044303(in Chinese)[戚聿波,周士弘,张仁和,张波,张云2014物理学报63 044303]

[14]Bonnel J,Gervaise C,Nicolas B,Mars J I 2012J.Acoust.Soc.Am.131 119

[15]Bonnel J,Thode A M,Blackwell S B,Kim K,Michael M A 2014J.Acoust.Soc.Am.136 145

[16]Zhang R H,Li F H 1999Sci.China A29 241(in Chinese)[张仁和,李风华1999中国科学A辑29 241]

[17]Wang D Z,Shang E C 2009Underwater Acoustics(2nd Ed.)(Harbin:Harbin Engineering University Press)pp628–640(in Chinese)[汪德昭,尚尔昌 2009水声学(第二版)(哈尔滨:哈尔滨工程大学出版社)第628—640页]

[18]Bonnel J,Gervaise C,Nicolas B,Mars J I 2010J.Acoust.Soc.Am.128 719

[19]Baraniuk R,Jones D 1995IEEE Trans.Signal Proc.43 2269

[20]Touze G L,Nicolas B,Mars J I 2009IEEE Trans.Signal Proc.57 1783

[21]Niu H Q 2014Ph.D.Dissertation(Beijing:University of Chinese Academy of Sciences)(in Chinese)[牛海强2014博士学位论文(北京:中国科学院大学)]

[22]Shang E C,Wu J R,Zhao Z D 2012J.Acoust.Soc.Am.131 3691

[23]Li X M,Zhang M H,Zhang H G,Piao S C,Liu Y Q,Zhou J B 2017Acta Phys.Sin.66 094302(in Chinese)[李晓曼,张明辉,张海刚,朴胜春,刘亚琴,周建波2017物理学报66 094302]

A passive range method of underwater source based on single hydrophone∗

Li Xiao-Man1)Piao Sheng-Chun1)2)Zhang Ming-Hui1)2)†Liu Ya-Qin1)Zhou Jian-Bo1)

1)(College of Underwater Acoustic Engineering,Harbin Engineering University,Harbin 150001,China)
2)(Acoustic Science and Technology Laboratory,Harbin Engineering University,Harbin 150001,China)

8 May 2017;revised manuscript

8 June 2017)

Aiming at the passive impulse wideband source range problem in shallow water waveguides,a passive source range method with single hydrophone which is applied to the shallow water waveguide with a bottom of liquid semi-in finite space is presented in this paper by combining the group delay theory and warping transformation.The receive signal is composed of several normal modes,and each mode represents many characteristics of the waveguide environment.Warping transformation is a good tool which can achieve the separation and extraction of normal modes from the received signal,and it is also an unitary and reversible transformation,so the warped signal of each normal mode can be recovered completely.The dispersion curves of normal modes can be extracted by warping transformation,and the relation between arrival time and frequency of each order normal mode can also be calculated,and then the time delay of arriving hydrophone between arbitrary two different normal modes is obtained.According to the group delay theory,different order normal mode has different arrival time at the same frequency,and the arrival time of normal mode is determined at its group speed when the distance between the source and hydrophone is certain.So the propagation range can be estimated when the time delay and the slow group speed difference between two different normal modes are known.When the waveguide environmental parameters are known,the slow group speed difference of arbitrary two normal modes can be calculated by KRAKEN.However,when the bottom parameters are unknown,the bottom reflection phase shift parameter is an important parameter describing the acoustic parameters of the bottom,and it contains nearly all the bottom information,what is more,the bottom reflection phase shift parameter is also a parameter that can be extracted by some experimental data easily.When the depth and the average sound speed of the water column are known,the slow group speed difference between two order normal modes can be represented by the sea floor phase shift parameter.Therefore,the source range can be represented by the bottom reflection phase shift parameter,the sea depth and the mean sound speed in the waveguide,and under this condition,the source location can be estimated by one single hydrophone.The effectiveness and accuracy of the method are proved by the numerical simulation results and sea experimental data processing,in which the signals are both received by a single hydrophone.The sea experimental data contain linear frequency modulation impulse source signal and explosion sound source signal,and the mean relative error of range estimation is less than 10%.

phase shift parameter,warping transformation,group delay,passive range

PACS:43.60.Jn,43.60.Ac,43.30.BpDOI:10.7498/aps.66.184301

*Project supported by the National Natural Science Foundation of China(Grant No.11474073).

†Corresponding author.E-mail:zhangminghui@hrbeu.edu.cn

(2017年5月8日收到;2017年6月8日收到修改稿)

针对浅海波导中宽带脉冲声源的被动测距问题,本文在群延迟理论的基础上,与warping变换处理相结合,提出了一种适用于浅海波导中宽带声源的单水听器被动测距方法.利用warping变换可以实现对脉冲声源接收信号各阶简正波的分离提取,对分离后的简正波进行时频分析处理可以得到各阶简正波到达时刻和频率之间的关系,即各阶简正波的频散曲线,从而得到任意两阶简正波到达接收水听器的时延差.海底相移参数P是描述海底地声参数的一个重要参量,包含了海底地声参数信息,在海底环境参数未知而P已知的情况下,利用P和简正波水平波数之间的关系可以求得任意两阶简正波的∆Sg,mn(群慢差).根据群延迟理论,利用得到的任意两阶简正波的时延和∆Sg,mn可实现利用单水听器对水下声源进行被动测距.本文提出的测距方法测量简单、计算方便,具有较强的实用意义.数值仿真和海上实验数据处理结果的测距误差都在10%以内,证明了该方法的有效性.

10.7498/aps.66.184301

∗国家自然科学基金(批准号:11474073)资助的课题.

†通信作者.E-mail:zhangminghui@hrbeu.edu.cn