随活性剂浓度变化的分离压对垂直液膜排液过程的影响∗

叶学民 杨少东 李春曦

(华北电力大学,电站设备状态监测与控制教育部重点实验室,保定 071003)

随活性剂浓度变化的分离压对垂直液膜排液过程的影响∗

叶学民 杨少东 李春曦†

(华北电力大学,电站设备状态监测与控制教育部重点实验室,保定 071003)

垂直液膜,活性剂浓度,活性剂类型,分离压

1 引 言

垂直液膜的排液过程是泡沫排液过程的简化模型[1],研究其影响因素及排液稳定性有利于揭示泡沫的衰变机理,为泡沫在工程中的高效应用,如泡沫灭火、泡沫浮选、石油开采、泡沫钻井、泡沫驱油等提供理论基础[2−4].

有关垂直液膜排液过程的研究已有不少报道.Mysels等[5]在1959年进行了著名的垂直悬挂液膜排液实验,他们将浸没在活性剂溶液中的金属丝框架提拉出来,观察上面附着的液膜的向下排液过程.结果表明,随溶液中活性剂浓度的不同,排液过程可能进行得相当缓慢(可长达1 h)或非常迅速(不到1 min液膜厚度可减少到不足1µm).实验还观察到,排液过程后期,特定情形下可形成稳定的极薄液膜,约为几十纳米,几乎不反射可见光,呈现透明状态,因拍照背景为黑色,所以液膜看上去也是黑色,故称“黑膜(black film)”.

目前普遍认为,影响垂直液膜排液过程的重要因素是分离压(disjoining pressure)和溶液的表面黏弹性质[3].分离压是保持液膜对立表面相互远离或靠近的压力,其本质是分子间作用力,在热力学上可描述为吉布斯自由能对液膜厚度的负导数π(h)=−∂G/∂h,主要由范德瓦耳斯引力、静电斥力和短程斥力组成[6,7],其中范德瓦耳斯力是普遍存在于固、液、气相的分子间或高分子官能团之间的长程物理力.气泡液膜和固体颗粒一样,在液相环境下呈现出一定的电性质,因而会在液膜表面上产生电势能,相应作用力称为静电作用力.一般认为,纯水中由于水偶极子在气液界面的吸附而使界面带负电荷[8],当纯水中加入表面活性剂时,活性剂的类型和浓度均会对静电作用力产生影响[6],进而影响分离压.Carey和Stubenrauch[9]通过实验测量发现,离子型活性剂溶液表面电荷随活性剂浓度的增加而提高,致使分离压中的静电斥力增大;而对非离子型活性剂溶液,因溶液表面的微弱电荷主要由水的负电荷构成,且不带电的非离子活性剂分子会吸附一部分水的表面电荷,因此随活性剂浓度的升高溶液表面电荷变少,导致静电斥力降低.

已有多名学者通过理论建模和数值模拟探讨了分离压对垂直液膜排液过程的影响.Schwartz和Roy[10]建立了两端固定的垂直液膜三方程模型(液膜厚度、不溶性表面活性剂浓度和表面滑移速度演化方程),并考虑了分离压作用,所得结果在界面移动性、界面形状及黑膜形成等方面与Mysels等[5]的实验结果定性地符合,但作者也提到今后应进一步考虑与活性剂浓度相关的分离压对排液过程的影响.Tabakova和Danov[7]采用润滑理论建立了金属框上的水平液膜排液过程模型,比较了不考虑分离压、仅考虑范德瓦耳斯引力和同时考虑分离压中的三种作用时液膜的排液特性,指出提高分离压中的斥力项可使引力项的失稳作用弱化,并预言可通过改变分离压中不同作用项的相对大小进而调控液膜排液过程.

出于对泡沫起泡性和泡沫稳定性的关注,另有学者针对溶液的表面黏弹性质对垂直液膜排液过程的影响开展了研究.最初,有学者认为加入不同表面活性剂后造成的溶液表面黏性的不同导致了泡沫的起泡性和泡沫稳定性的差异.其中Braun课题组[11−14]在2000—2004年发表了多篇研究,探讨了表面黏度为常数、表面黏度随活性剂浓度变化等多种情形下垂直液膜的排液过程,虽然计算结果与实验结果也有较好的符合,但实验中观察到的现象仍有许多未能得到解释,如液膜底部的复杂结构、不同种类活性剂溶液形成的液膜的破断时间及稳定性存在很大差异等.随着对表面弹性实验测量的普遍开展,有部分学者认为溶液的表面弹性较表面黏性对垂直液膜排液具有更为重要的影响.Sett等[15]分别采用不同浓度(低于、等于和高于临界胶束浓度(CMC))的非离子、阳离子和阴离子表面活性剂进行了垂直液膜排液过程实验,对比了活性剂种类对液膜排液过程的影响,结果表明非离子活性剂C8E4的液膜存续时间较长(98—189 s),含阳离子和阴离子活性剂的液膜存续时间适中(60—100 s),而另一种非离子表面活性剂P-123的排液时间则较短(70—78 s).此外,不同种类活性剂溶液形成的液膜排液过程中黑膜的出现早晚和黑膜的扩展速度也不同,这是由于不同种类活性剂溶液的表面弹性不同所致.类似地,Saulnier等[16]也采用不同表面弹性和浓度(均超过CMC)的表面活性剂开展垂直液膜排液实验,表明提拉金属框后,阴离子表面活性剂十二烷基硫酸钠(SDS)溶液形成的液膜中黑膜长度可长达1.5 mm,而非离子活性剂溶液C12E6形成的黑膜长度则较短,为0.5 mm左右,作者认为SDS和C12E6均具有较高的表面弹性,而另一种具有较低表面弹性的阳离子活性剂C10TAB的实验结果则因液膜破断太快,未能测量黑膜长度.而在另一实验中,Saulnier等[17]却发现,虽然C12E6和C12G2均为非离子活性剂,表面弹性非常相近,液膜的存续时间基本相同,但排液过程中C12E6溶液黑膜长度较小,即黑膜稳定性较差,导致起泡性实验中C12E6产生得很多气泡很快就破灭,因而其起泡性显著差于C12G2.由此可见,表面弹性是否为影响垂直液膜排液的关键因素还存在诸多争议.

综上所述,黑膜的形成和存续时间与垂直液膜排液过程中液膜稳定性密切相关,而黑膜的厚度范围正是分离压起重要作用的范围,同时受活性剂种类影响,分离压与活性剂浓度间有不同的关联性.因此从随活性剂浓度变化的分离压角度对不同种类的活性剂溶液排液过程进行建模分析具有重要的意义.

本文基于文献实验结果建立了受活性剂浓度影响的分离压模型,采用数值模拟方法,全面分析当分离压中的斥力项随当地活性剂浓度变化时的垂直液膜排液特征,揭示分离压影响液膜排液过程的内在机理.

2 物理模型

图1为两端固定的垂直液膜排液过程,液膜置于无黏性气体中,假设液体运动黏度和密度均为常数.液膜表面厚度为y=±h(x,t),关于中心线y=0对称,因此只需考虑一侧液膜厚度变化即可.排液过程中,雷诺数Re=Uh0/µ≪1(U为特征速度,h0为液膜特征厚度,µ是动力黏度),且ε=h0/L≪1,因此适用于润滑理论.

图1 垂直液膜排液过程示意图 (a)初始时刻;(b)排液过程;(c)速度分布Fig.1. Schematic diagram of the vertical film drainage:(a)The initial state of film;(b)the process of drainage;(c)the distribution of interface velocity.

控制方程包括连续性方程和运动方程:

式中,下角标表示对该参数求偏导,下同.边界条件为

自由液面上的运动学条件为

切向应力τ和表面压强ps满足力平衡条件:

当表面黏度很小时,可将垂直方向上的排液速度u分解为滑移速度u0和剪切速度u1[10,18],即

且满足在y=h处,u1=0.因此u0也可视为液膜表面速度.

采用如下无量纲变换式(其中上标“∗”表示无量纲量):

将(8)和(9)式代入(1)—(7)式可得无量纲控制方程组为

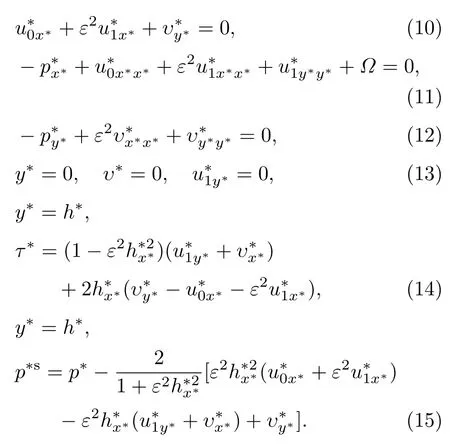
利用润滑理论[19,20],结合

其中Q∗为体积流量.则无量纲液膜厚度和切应力可表示为

(7)式中,液膜表面压强由毛细力和分离压组成,

式中,κ为液膜表面曲率,κ=hxx/(1+h2x)3/2;σ为表面张力,考虑到表面张力相对于液膜曲率变化较小,故σ用σ0代替.当液膜中含表面活性剂时,表面张力与活性剂浓度间的关系为

其中Σ为与浓度有关的系数.

在液膜表面,切应力τ与表面张力梯度σx近似平衡,因此结合(20)式可得

为便于与不受活性剂影响的分离压模型进行比较,采用如下模型[10]:

(22)式右侧分别代表范德瓦耳斯引力和静电斥力,即略去了短程斥力(液膜厚度为几个纳米时才需考虑[21]);heq为平衡液膜厚度;A1,A2分别为Hamaker系数和与静电作用斥力有关的强度系数.以文献[9]的实验结果为基础,令静电斥力强度系数A2与活性剂浓度相关,而A1为常数.为此,令A1=10,A2=10+αΓ,式中α为斥力关联系数,α取正值时,对应静电斥力随浓度升高而增大的离子型活性剂;α取负值时,对应静电斥力随浓度升高而降低的非离子型活性剂.

由于本文研究中活性剂为不溶性,即浓度Γ仅仅存在于液膜表面,不存在y方向上的扩散.另外已有研究表明[10],提拉金属框形成的垂直液膜在展向上的流动均匀一致,可忽略其展向上的变化.因此Γ只是x,t的函数,故活性剂浓度的迁移扩散方程可写为

式中,D为扩散系数.

联立(17)—(24)式,可得液膜厚度h、活性剂浓度G和表面速度u0的非线性偏微分方程组(为描述方便,以下省略上标“∗”):

边界条件的选取对液膜演化至关重要.本文针对排液实验中金属框已经完全从活性剂溶液中提拉出来,底端已与溶液池脱离,且其上附着液体的质量已不是很多,即便垂直排液导致部分液体在金属框下部堆积,液体也不会脱离金属框而滴落的情形,基于Schwartz和Roy[10],Moulton和Lega[22,23]研究中采用的无滑移边界条件,将上下两端处液膜厚度设置为恒定值,即

两端既无流体流动也无活性剂流动,

无量纲初始条件

3 数值模拟

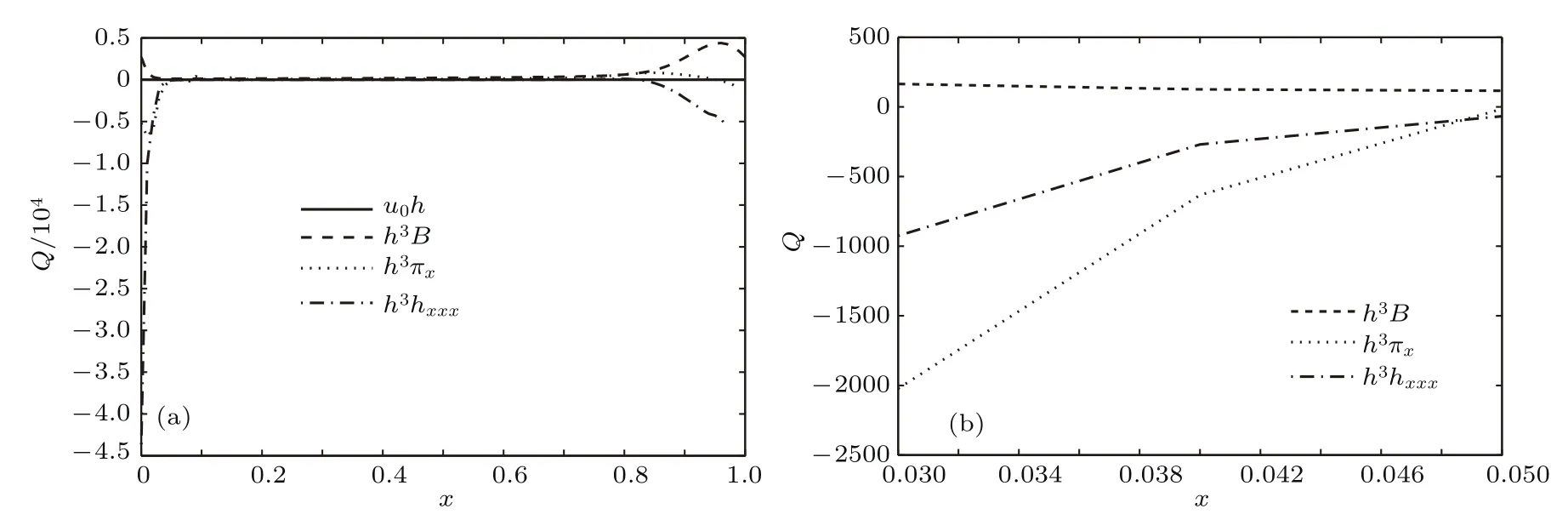
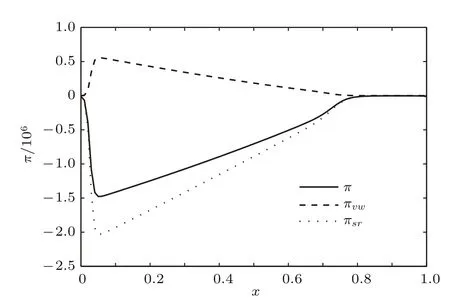
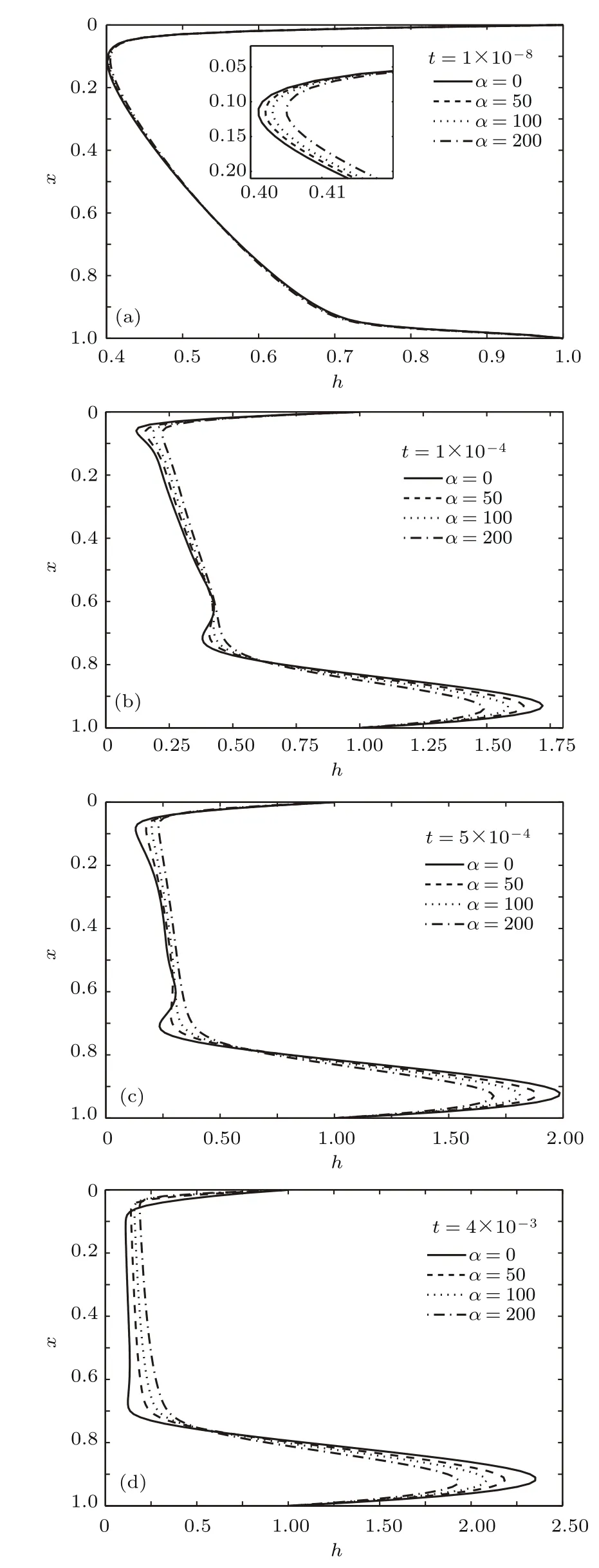
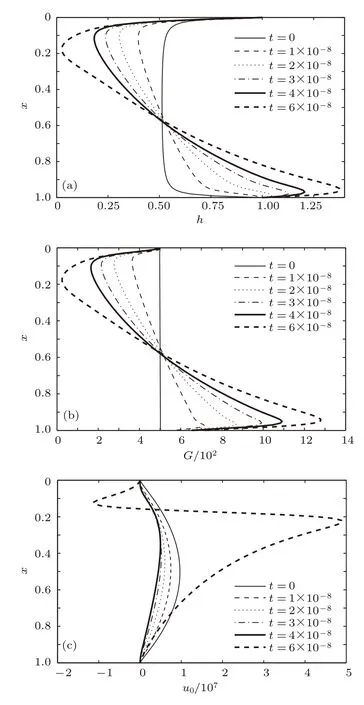
采用FREEFEM程序求解演化方程组(25)—(27)式.选取(0

表1 典型尺度及无量纲参数数值范围Table 1.Typical scale and dimensionless parameters in the experiment.

初始垂直液膜厚度为

当表面切应力与重力数量级相当时,将对液膜产生很强的“迟滞(retardation)”效应,即

因而可得

为模拟含活性剂液膜的垂直流动特征,定义初始活性剂浓度比修正邦德数小一个量级,文中取500.

4 模拟结果与分析

4.1 分离压与活性剂浓度无关时的排液过程

为与分离压随活性剂浓度变化时的排液历程进行对比,首先讨论分离压与活性剂浓度无关时的情形.如图2所示,在t=0—4×10−3范围内,排液过程可分为两个阶段:首先是厚膜阶段(t=0—1×10−8),此阶段受重力作用液膜顶端迅速被拉薄,而在底端液膜迅速增厚,随排液持续,上部液膜厚度逐渐减小,之后进入薄膜阶段.受边界条件(28)式及质量守恒影响,液膜顶部形成半月形区,底部因液体累积形成不断膨胀的球形凸起.中间部分为液膜曲率较小、形状近乎直线的区域.排液过程导致在半月形区域结束处液膜厚度出现最小值,且在排液后期,中间部分有相当长的区域液膜厚度与最小液膜厚度非常接近,这与实验中的“黑膜(black film)”区域相对应[15−17].为此,下文以“黑膜(black film)”区泛指最小液膜厚度附近的区域,该区域液膜厚度很薄,但非常稳定;随时间持续,“黑膜(black film)”区不断向下扩展,呈现犹如“千钧系于一发”的状态,最后排液达到稳定状态;此时表面速度相比于演化早期已大大减小(图2(d)),液膜表面趋于“刚性化”.分离压与活性剂浓度无关时排液过程的计算结果与Schwartz和Roy[10]的计算结果一致.

图2 分离压与活性剂浓度无关时的排液过程 (a)液膜厚度;(b)活性剂浓度;(c)早期表面速度;(d)后期表面速度Fig.2.Evolution of film drainage under the disjoining pressure independent of the surfactant concentration:(a)Film thickness;(b)surfactant concentration;(c)surface speed of early time;(d)surface speed of later time.

图2(b)中,在演化后期活性剂浓度峰谷差减小的原因可解释如下:最初由于表面活性剂分布均匀,中间部分的液膜厚度也分布均匀,液体受重力作用向下流动,使活性剂逐渐在液膜底部积累;同时逐渐形成了自下而上的活性剂浓度梯度,由此产生Marangoni效应,因此液膜有自下而上流动的驱动力,但最初时间段内该驱动力还较弱,结合图2(c)和图2(d)可看出,液膜表面流动速度越来越慢,直到t=1×10−4时,Marangoni效应诱导的驱动力已经足够强大,致使液膜表面停止向下流动;此后,液膜表面上的流体携带活性剂分子一起向上移动,从而使活性剂浓度峰谷差减小.但液膜内部的流动速度还包含剪切速度的成分,其方向向下,所以t>1×10−4后中间区域的液膜厚度仍然继续减薄.

由于本文计算中边界条件设置为上下两端处液膜厚度恒定,因此随着排液不断进行,液体在液膜底部不断堆积,形成了巨大的球形凸起,且膨大凸出的程度随时间演化不断增加.在采用同样边界条件的Schwartz和Roy[10],Moulton和Lega[22,23]的研究结果中也观察到了球形凸起的存在.由于本文关注的是液膜中上部分,特别是黑膜所在的液膜上部,因此下部的膨大凸出部分对本文的研究和分析不会产生重要影响.

图3进一步示出了薄膜阶段(t>1×10−8)最薄液膜厚度hmin变化趋势.图3表明hmin随时间逐渐减小,在t=8×10−7接近“黑膜(black film)”,并随时间不断变薄,之后因受表面流体逆流影响“黑膜(black film)”厚度hb又有所增加,最后再减小并趋于稳定.

图3 薄膜阶段最小液膜厚度的演化历程Fig.3.Evolution of the minimum film thickness in the thin film stage.

在(25)式中,u0h为表面速度项,h3B为重力影响项,h3πx为分离压影响项,h3hxxx为毛细力影响项.为深入分析上述各项对排液过程的不同影响,图4给出了t=4×10−3时在液膜不同位置处的各影响项.图4(a)表明在液膜中部,剪切流各项(即重力影响、分离压影响和毛细力影响)几乎均为0,对液膜排液过程几乎没有影响;而在液膜底端附近产生一球形凸起特征,液膜质量几乎均集中于此,即重力项对排液产生显著影响;为平衡重力,产生了大小相同、但方向相反的毛细力作用;在液膜底端,液膜厚度处于分离压作用范围之外,故分离压不会影响底端液膜排液过程.但在“黑膜(black f i lm)”区,因液膜厚度处于分离压作用范围内,故分离压对顶端“黑膜(black film)”区排液过程产生明显影响.由图4(b)及图5可知,在“黑膜(black f i lm)”区,因分离压中的静电斥力大于范德瓦耳斯引力,使分离压整体表现为阻力作用,导致液膜排液产生逆流,由此减缓液膜排液速度,起到增强液膜排液稳定性的作用.

图4 活性剂浓度与分离压无相关时表面速度、重力、分离压和毛细力的分布特征(t=4×10−3)Fig.4.Distribution of surface velocity,gravitational force,disjoining pressure,and capillary force at t=4×10−3under the disjoining pressure independent of the surfactant concentration.

图5 t=4×10−3时分离压沿流动方向上的分布Fig.5. Distribution of disjoining pressure along streamwise direction at t=4×10−3.

4.2 分离压与活性剂浓度相关时的排液过程

由(22)式可知,当α=0时,静电斥力将受活性剂浓度影响,α值的正负和大小可反映活性剂种类和浓度对其的不同影响.图6为α=200,即静电斥力与活性剂浓度正相关时液膜厚度、活性剂浓度及表面速度的演化历程.与4.1节对比可知,在受活性剂浓度影响的分离压作用下的液膜排液过程,其液膜厚度演化总体趋势基本一致,“黑膜”形成时间也大约在10−4的量级.但二者在液膜厚度数值上却有明显区别.比较t=4×10−3时的液膜厚度剖面可知,当分离压不随活性剂浓度变化时,“黑膜”厚度约为0.1,且自x≈0.1—0.7的区域内液膜厚度均非常接近“黑膜”厚度,即“黑膜”长度约为0.6;而分离压受活性剂浓度影响时,液膜顶端x≈0.1处“黑膜”厚度约为0.2,且随x增加,液膜厚度缓慢增加,x≈0.7处,液膜厚度已经增加至0.3,即当考虑活性剂浓度对分离压影响时“黑膜”区域的液膜厚度增加.显然当分离压随活性剂浓度发生变化时,液膜排液过程减慢,液膜稳定性得到增强.

图6 活性剂浓度与分离压正相关时的排液过程 (a)液膜厚度;(b)活性剂浓度;(c)早期表面速度;(d)后期表面速度Fig.6.Evolution of film drainage under the positive correlation of disjoining pressure with surfactant concentration:(a)Film thickness;(b)surfactant concentration;(c)surface speed of early time;(d)surface speed of later time.

对比图7(a)和图4(a)可知,各影响项沿排液方向上的变化趋势大体一致,但由于分离压随活性剂浓度发生变化,因此分离压对液膜排液的影响也明显不同.从图7(b)和图8可发现,此时分离压中静电斥力大于范德瓦耳斯力,从而使分离压呈现阻力效应,且分离压作用范围从液膜顶部扩大至距液膜顶端x≈0.8处,进一步阻碍液膜排液、变薄.此外,分离压影响液膜排液逆流的体积流量也得到提高,如x≈0.03处,当分离压不受活性剂浓度影响时,逆流流量约为180,而当考虑活性剂浓度影响时,分离压效应引起的排液逆流流量约为2000,且分离压引起排液逆流的影响超过了毛细力项的影响.

图7 活性剂浓度与分离压正相关时表面速度、重力、分离压和毛细力的分布特征(t=4×10−3)Fig.7.Distribution of surface velocity,gravitational force,disjoining pressure,and capillary force at t=4×10−3under the positive correlation of the disjoining pressure with surfactant concentration.

图8 正相关时分离压沿整个液膜分布(t=4×10−3)Fig.8. Distribution of disjoining pressure along streamwise direction at t=4×10−3under the positive correlation of the disjoining pressure with surfactant concentration.

α值的大小代表静电斥力与活性剂浓度关联强度的强弱,α越大表示静电斥力受活性剂浓度影响程度愈突出,图9为α=0,50,100和200时在四个典型时刻下的液膜厚度分布.在演化初期(t=1×10−8),垂直液膜在重力作用下快速变薄,演化至薄膜阶段后(t=8×10−7),液膜是否破断将取决于“黑膜”是否发生破断[17],而由图10可知,当t=4×10−3时,不同α下的液膜最薄处均未发生破断,即排液过程仍持续进行.由图9可知,在同一时刻下,不同α情形下的液膜排液过程不同,随α增大,在同一位置处的液膜厚度愈大.由此说明,当活性剂浓度与静电斥力具有正相关影响时,分离压具有增强液膜稳定性的作用,且随α增大,该作用愈加明显,这与文献[7]的计算结果一致,尽管本文所用分离压模型与文献[7]不同.

图11为α=−200,即静电斥力与活性剂浓度负相关时的垂直液膜排液过程.图11表明:排液初期液膜顶部区域在重力作用下迅速变薄,液膜顶端处的活性剂在排液流体携带下向底端聚集,顶部活性剂浓度不断降低;在最小液膜厚度附近液膜表面速度呈现较大梯度,其以上区域表面速度呈现负值,即此处液膜中流体发生逆流,而在最小液膜厚度以下区域,流体在重力作用下继续向下流动.随时间持续,最小液膜厚度处的液膜不断变薄,并未形成稳定的“黑膜”.在t=6.1×10−8时,液膜发生破断,排液过程终止.与图2和图6相比,静电斥力与活性剂浓度呈负相关时的垂直液膜排液时间明显较短,且此过程中最小液膜厚度附近液膜表面速度梯度较大,容易受到“拉扯”作用,从而发生破断.

为揭示液膜破断前各影响因素的特征,图12给出了在t=6×10−8时表面速度、重力、分离压和毛细力分布.图12(a)表明,在影响垂直液膜排液体积流量的各因素中,滑移流(u0h)几乎起决定性作用.图12(b)为最小液膜厚度附近剪切流中各因素的影响,与图4(b)和图7(b)对比可知,在分离压随活性剂浓度变化呈负相关的情形下,分离压不会引起液膜排液逆流现象,而是起加速液膜排液作用,致使液膜快速变薄,进而发生破断.此时,由图13知,分离压中范德瓦耳斯引力大于静电斥力,从而使分离压整体呈现引力效应,也有文献[25]称之为结合压.这与文献[25]得出的结合压会加速液膜流动演化的结论一致.

图9 不同α(正相关)下的液膜厚度分布(t=1×10−8,1×10−4,5×10−4,4×10−3)Fig.9.Evolution of film thickness under different α values(positive correlation)at t=1×10−8,1×10−4,5×10−4and 4×10−3,respectively.

图10 α=0,50,100和200时薄膜阶段最薄液膜厚度的演化历程Fig.10.Evolution of the thinnest film thickness when α is 0,50,100,200,respectively in the thin film stage.

图11 活性剂浓度与分离压负相关时的排液过程 (a)液膜厚度;(b)活性剂浓度;(c)表面速度Fig.11.Evolution of film drainage under the negative correlation of disjoining pressure with surfactant concentration:(a)Film thickness;(b)surfactant concentration;(c)surface speed.

图12 活性剂浓度与分离压负相关时表面速度、重力、分离压和毛细力的分布特征(t=6×10−8)Fig.12. Distribution of surface velocity,gravitational force,disjoining pressure,and capillary force at t=6×10−8under the negative correlation of the disjoining pressure with surfactant concentration.

图13 负相关时分离压沿整个液膜分布(t=6×10−8)Fig.13. Distribution of disjoining pressure along streamwise direction at t=6×10−8under the negative correlation of the disjoining pressure with surfactant concentration.

图14对比了不同负相关情形下的垂直液膜厚度演化特征.图14表明,随负相关系数α绝对值增大,液膜顶端“黑膜”区厚度减小速度加快,液膜排液过程更容易终止.由此可知,对于一些含有非离子型表面活性剂情形下的垂直液膜排液过程,分离压将加速液膜排液过程,致使液膜失稳;且随α绝对值增大,排液过程加快,失稳性增强.

图14 不同α(负相关)下的液膜厚度分布(t=1×10−8,2×10−8,4×10−8,6×10−8)Fig.14.Evolution of film thickness under different α values(negative correlation)at t=1×10−8,2×10−8,4×10−8and 6×10−8,respectively.

5 讨 论

4.2节分别考虑了分离压与活性剂浓度正相关和负相关两种情形下垂直液膜的排液过程,其中与活性剂浓度正相关和负相关的分离压模型分别受文献[9]中的离子型和非离子型活性剂溶液的分离压测量结果启发.本文结果表明,在正相关情形下,液膜存续时间较长,更为稳定,且计算结果与Sett等[15]和Saulnier等[16]采用阴离子表面活性剂SDS进行实验的结果非常符合.对于负相关情形,本文结果为液膜在较短时间内破断,与Sett等[15]实验中非离子表面活性剂P-123的情形和Saulnier等[16]实验中C12E6的情形也非常一致,但与Sett等[15]实验中非离子表面活性剂C8E4的情形不符,而Sett等[15]实验中计算得到的C8E4的表面弹性较P-123要高一个数量级.对于阳离子表面活性剂,从分离压与活性剂浓度的相关性来看,与阴离子表面活性剂并无差别,但排液实验中液膜的存续时间方面,同为阳离子活性剂的十二烷基三甲基溴化铵(DTAB)和C10TAB却相差甚远.Sett等[15]的实验中,阳离子活性剂DTAB形成的液膜与阴离子活性剂SDS形成的液膜存续时间相当,而在Saulnier等[16]的实验中,阳离子活性剂C10TAB形成的液膜存续时间却异常短暂,一些学者[26,27]认为C10TAB溶液的表面弹性较低,这导致其形成的液膜快速破断.上述实验结果表明,应在根据表面活性剂种类判断其对分离压影响的基础上,再进一步考虑分离压和溶液表面弹性的协同耦合作用.

由于分离压对于数十纳米数量级的黑膜具有非常重要的影响,因而Saulnier等[16]的实验中黑膜长度数据更能说明本文所建分离压模型对排液过程影响的合理性.SDS和C12E6均具有较高的表面弹性,但阴离子表面活性剂SDS溶液形成的黑膜长度约为非离子活性剂C12E6溶液形成黑膜长度的3倍,说明随活性剂浓度呈现不同变化趋势的分离压对泡沫稳定性确实具有重要影响.

6 结 论

1)垂直液膜的排液过程通常经历两个阶段:首先是厚膜阶段,此时重力对排液过程起主导作用;在随后的薄膜阶段,毛细作用和分离压作用影响逐渐增大,其中分离压将控制液膜的演化历程.

2)当分离压与活性剂浓度正相关时,随斥力关联系数α增大,液膜的排液和变薄过程得以减缓,由此增强了液膜稳定性;当分离压与活性剂浓度负相关时,随斥力关联系数α绝对值增大,液膜排液过程加速,由此加大液膜失稳的风险.

3)文中所得结果与文献中的部分实验结果相符合,表明分别与活性剂浓度正、负相关的分离压作用确实对某些阴离子型活性剂和非离子型活性剂泡沫的稳定性具有重要影响.

4)文中建立的与活性剂浓度相关的分离压模型尚无法解释部分阳离子型和非离子型活性剂液膜在排液实验中的现象,表明今后的计算模型中应该进一步考虑活性剂分子的结构、分离压的多种作用项及分离压与表面弹性的耦合作用.

[1]Li G S 2013Ph.D.Dissertation(Xuzhou:China University of Miningand Technology)(in Chinese)[李国胜2013博士学位论文](徐州:中国矿业大学)

[2]Liang M Q,Yin H Y,Feng Y J 2016Acta Phys.Chim.Sin.32 2652(in Chinese)[梁梅清,殷鸿尧,冯玉军 2016物理化学学报32 2652]

[3]Wang J,Nguyen A V,Farrokhpay S 2016Adv.Colloid Interfac.228 55

[4]Du D X,Zhang N,Sun R,Wang C C,Zhang J,Li Y G 2016CIESC J.67 181(in Chinese)[杜东兴,张娜,孙芮,王程程,张健,李莺歌2016化工学报67 181]

[5]Mysels K J,Shinoda K,Frankel S 1959Soap Films:Studies of Their Thinning and a Bibilography(New York:Pergammon)p116

[6]Bhakta A,Ruckenstein E 1997Adv.Colloid Interfac.70 1

[7]Tabakova S S,Danov K D 2009J.Colloid Interface Sci.336 273

[8]Manev E D,Pugh R J 1991Langmuir7 2253

[9]Carey E,Stubenrauch C 2010J.Colloid Interface Sci.343 314

[10]Schwartz L W,Roy R V 1999J.Colloid Interface Sci.218 309

[11]Naire S,Braun R J,Snow S A 2000J.Colloid Interface Sci.230 91

[12]Naire S,Braun R J,Snow S A 2001Phys.Fluids13 2492

[13]Braun R J,Snow S A,Naire S 2002J.Eng.Math.43 281

[14]Naire S,Braun R J,Snow S A 2004J.Comput.Appl.Math.166 385

[15]Sett S,Sinha-Ray S,Yarin A L 2013Langmuir29 4934

[16]Saulnier L,Champougny L,Bastien G,Restagno F,Langevin D,Rio E 2014Soft Matter10 2899

[17]Saulnier L,Boos J,Stubenrauch C,Rio E 2014Soft Matter10 7117

[18]De Wit A,Gallez D,Christov C I 1994Phys.Fluids6 3256

[19]Zhao Y P 2012Physical Mechanics of Surface and Interface(Beijing:Science Press)pp185,186(in Chinese)[赵亚溥2012表面与界面物理力学(北京:科学出版社)第185,186页]

[20]Li C X,Pei J J,Ye X M 2013Acta Phys.Sin.62 214704(in Chinese)[李春曦,裴建军,叶学民 2013物理学报 62 214704]

[21]Claesson P M,Kjellin M,Rojas O J,Stubenrauch C 2006Phys.Chem.Chem.Phys.8 5501

[22]Moulton D E,Lega J 2013Eur.J.Appl.Math.24 887[23]Moulton D E,Lega J 2009Physica D238 2153

[24]Sakata E K,Berg J C 1972J.Colloid Interface Sci.40 99

[25]Ye X M,Jiang K,Li C X 2013CIESC J.64 3581(in Chinese)[叶学民,姜凯,李春曦 2013化工学报 64 3581]

[26]Bergeron V 1997Langmuir13 3474

[27]Bykov A G,Lin S Y,Loglio G 2010Colloids Surf.A:Physicochem.Eng.Asp.354 382

Effect of concentration-dependent disjoining pressure on drainage process of vertical liquid film∗

Ye Xue-Min Yang Shao-Dong Li Chun-Xi†

(Key Laboratory of Condition Monitoring and Control for Power Plant Equipment,North China Electric Power University,Baoding 071003,China)

3 March 2017;revised manuscript

10 May 2017)

For the drainage under the gravity of a vertical foam film containing insoluble surfactant,an improved concentrationdependent disjoining pressure model is formulated based on the published experimental results.The lubrication theory is used to establish the evolution equations of the film thickness,the surface concentration of insoluble surfactant,and the surface velocity,and the evolution characteristics of the film under different disjoining pressures are simulated numerically.The results show that the drainage process of a vertical liquid film generally undergoes two stages:the f i rst stage is the thick film stage and the gravity plays a leading role in the drainage process;the subsequent stage is the thin film stage,the effects of capillary pressure and disjoining pressure increase gradually,and the disjoining pressure dominates the evolution of the film.The disjoining pressure effect is closely related to surfactant type and the correlation strength between the surfactant concentration and electrostatic repulsion force of disjoining pressure.For the ionic surfactant,electrostatic repulsion force increases with the increase of the surfactant concentration,but it is opposite for the nonionic surfactant.It is likely that the free hydroxide ions,which are considered to render the surface negatively charged,are partly adsorbed by the nonionic surfactant.So the surface charge of the foam film decreases as the concentration of the nonionic surfactant increases,resulting in a decrease in electrostatic repulsion.Therefore,some ionic surfactants can improve the stability of liquid film drainage and slow down the drainage process,while the effects of some nonionic surfactants are opposite.When the disjoining pressure is positively correlated with surfactant concentration,with the increase of correlation strength coefficientα,the thinning and drainaging processes of the film tend to slow down,hence the stability of the film is enhanced.When the disjoining pressure is negatively correlated with surfactant concentration,with the increase of the absolute value ofα,the drainage process of the film is accelerated and the risk of film rupture is augmented.The results obtained in this paper are consistent with some of the experimental results,indicating that the concentration-dependent disjoining pressure is indeed an important factor in maintaining the stability of foam film containing some certain anionic or nonionic surfactants.The improved concentration-dependent disjoining pressure model established in this paper could not explain the phenomena of parts of cationic nor non-ionic surfactant film in drainage experiments.It can be inferred that the structure of surfactant molecule,the more detailed disjoining pressure model and the coupling of the disjoining pressure and surface elasticity should be considered in the future work.

vertical film,surfactant concentration,surfactant type,disjoining pressure

PACS:47.61.–k,47.85.mf,47.61.fg,47.55.dkDOI:10.7498/aps.66.184702

*Project supported by the National Natural Science Foundation of China(Grant No.11202079)and the Natural Science Foundation of Hebei Province,China(Grant No.A2015502058).

†Corresponding author.E-mail:leechunxi@163.com

(2017年3月3日收到;2017年5月10日收到修改稿)

针对含不溶性活性剂的垂直液膜排液过程,基于文献实验结果进一步完善了受活性剂浓度影响的分离压(disjoining pressure)模型,应用润滑理论建立了液膜厚度、活性剂浓度和液膜表面速度的演化方程组,通过数值计算分析了在不同分离压作用下含不溶性活性剂液膜的演化特征.结果表明,垂直液膜的排液过程通常经历两个阶段:首先是厚膜阶段,此时重力对排液过程起主导作用.在随后的薄膜阶段,毛细作用和分离压作用影响逐渐增大,其中分离压将控制液膜的演化历程.分离压对垂直液膜排液过程的影响与活性剂类型及活性剂浓度与静电作用力的关联强度密切相关.当分离压与活性剂浓度正相关时,随斥力关联系数α增大,液膜的排液和变薄过程得以减缓,由此增强了液膜稳定性;当分离压与活性剂浓度负相关时,随斥力关联系数α绝对值增大,液膜排液过程加速,由此加大液膜失稳的风险.

10.7498/aps.66.184702

∗国家自然科学基金(批准号:11202079)和河北省自然科学基金(批准号:A2015502058)资助的课题.

†通信作者.E-mail:leechunxi@163.com