深水J-Lay大直径薄壁管道的理论分析及数值模拟*

张永强

(1.华南理工大学 土木与交通学院，广东 广州 510640；2.广州打捞局，广东 广州 510260)

深水J-Lay大直径薄壁管道的理论分析及数值模拟*

张永强1,2

(1.华南理工大学 土木与交通学院，广东 广州 510640；2.广州打捞局，广东 广州 510260)

建立了考虑Brazier效应的管道非线性微分方程，利用奇异摄动理论得到了J-Lay管道形态的解析解，应用迭代法求出管道的弯矩、轴力等关键参数，同时采用有限元法对管道理论解的正确性进行了验证，研究了张紧力、水深以及水流力对J-Lay管道形态和弯矩的影响.理论结果表明：J-Lay管道铺设过程中，其弯矩的峰值总是出现在触底点(TDP)附近的管段,在一定的范围内增加张紧力，管道的形态越平缓、弯矩峰值越小，对铺管越有利；其他参数不变、增加水深时，管道弯矩峰值并不是单调地增加；水流力与铺管方向相反时会增加管道的弯矩峰值，对铺管不利.

薄壁管道；非线性；奇异摄动；解析解；弯矩

深水环境下的管道铺设(特别是J-Lay管道的铺设)问题引起了学者们的广泛关注.Robert等[1]利用有限元法分析了不同管道的极限状态.黄钰等[2]采用有限元法对S-Lay管道进行动态分析.龚顺风等[3]用悬链线理论对S-Lay管道进行静力分析.朱达善等[4]采用奇异摄动法对管道铺设进行静力分析，但未考虑水流力对管道形态的影响，且其摄动解不符合海底边界条件.韩强等[5]用奇异摄动理论得到了深海S-Lay管道的形态解析解.周巍伟等[6]采用三维非线性梁单元对深水海底管道S型铺设的影响因素开展动态有限元分析.J-Lay铺管法其实质也是张力铺管法中的一种，通过调节铺管塔的倾角以及调节张紧力来完成管道的铺设，与传统的S-Lay铺管法相比更适合于深水作业.Yuan等[7]给出了在J-Lay管道触底点(TDP，Touch Down Point)附近区域受海底反作用力下管道形态的解析解.Han等[8]研究了J-Lay铺管塔设计参数的选取问题.Lenci、康庄等[9-10]将J-Lay管线分为悬链线和大变形梁两段进行分析，得到了管道形态的解析解.Wang等[11]采用奇异摄动法研究了J-Lay管道形态的问题，但未考虑管道的Brazier效应[12].

文中在前人研究的基础上，考虑J-Lay管道截面的Brazier非线性效应、水流力以及管道边界条件对铺管的影响，采用奇异摄动原理得到了管道非线性控制方程的摄动解，利用有限元法对深水环境铺管过程进行数值模拟，通过奇异摄动解和有限元法(FEM)解的对比来验证文中理论的正确性；并对铺管参数的敏感性进行了分析.

1 非线性微分方程的建立

如图1所示，深水环境J-Lay管道铺设过程中水深为h，铺管船干舷高为h0，管道悬跨段x轴方向的长度为L，海床斜度和管道入水角分别为φ0和φi，其中管道的外直径为D，壁厚为t，弹性模量为E，泊松比为μ.由文献[13]可得

(1)

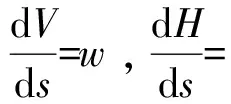
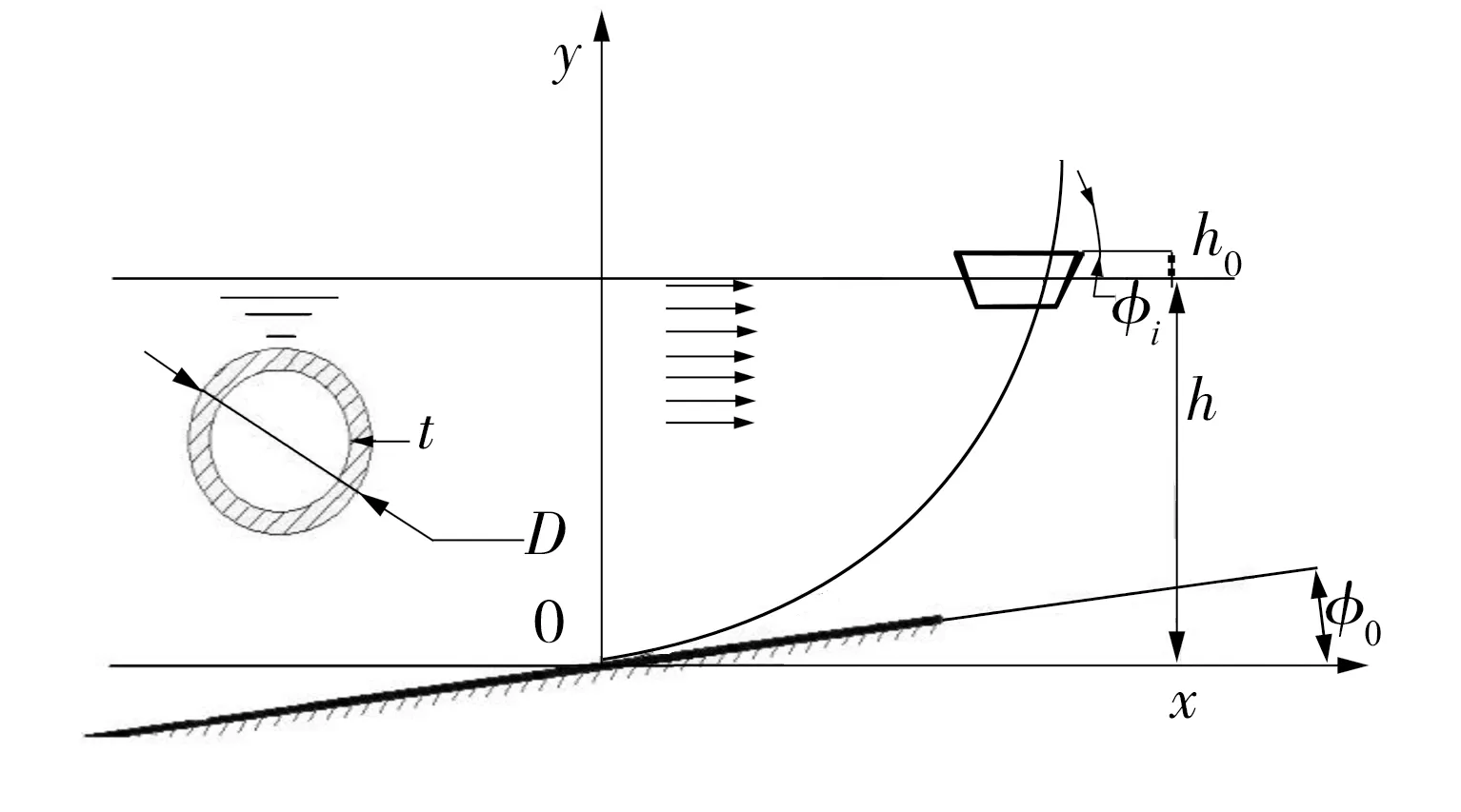
图1 J-Lay铺管示意图Fig.1 Sketch map of J-Lay pipelines

考虑Brazier非线性效应，此时管道截面的弯矩-曲率是非线性关系，由Brazier[14]长管壳弯矩-曲率关系式，有

M=EI0κ(1-c0κ2)

(2)

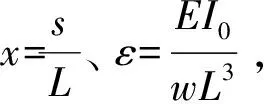
εθ″-3c1εθ′2θ″+(ab+εq+x)cosθ-(a-cx)sinθ=0

(3)

H0为管道初始水平力.

2 J-Lay管道的奇异摄动解

摄动法是求解含有小参数ε非线性微分方程有效的方法.正则摄动法在外部区域可以得到很好的运用，但在边界层往往很难满足要求，而奇异摄动法刚好能解决这一问题[15].

2.1 非线性微分方程的外部解

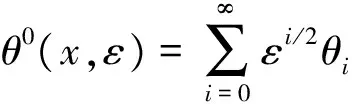
(1)0阶ε0

(ab+x)cosθ0-(a-cx)sinθ0=0

(4)

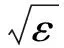
[(x+ab)sinθ0+(a-cx)cosθ0]θ1=0

(5)

(3)2阶ε

[(ab+x)sinθ0+(a-cx)cosθ0]θ2=

(6)

根据式(4)-(6)，可得

(7)

由此可得J-Lay管线的非线性控制微分方程的外部解为

(8)

2.2 非线性微分方程的内部解(x=0)

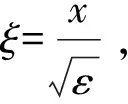
(9)

2.3 非线性微分方程的内部解(x=1)

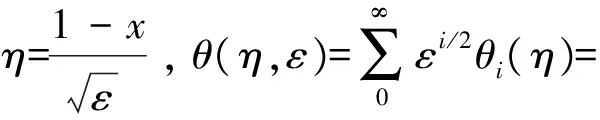
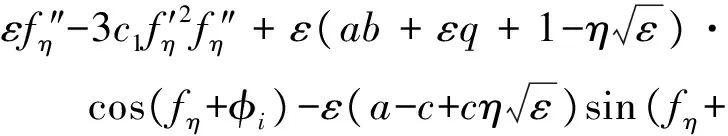
(10)

(1)0阶(ε0)

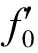
(11)

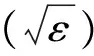
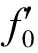
(12)

(3)2阶(ε)

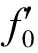
(c-a)sin (f0+φi)+(ab+1)cos (f0+φi)=0

(13)

(4)3阶(ε3/2)

(abf1+f1)sin(f0+φi)-cηsin(f0+φi)-

(af1-cf1+η)cos(f0+φi)=0

(14)

(5)4阶(ε2)

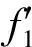
(abf2+f2-ηf1)sin(f0+φi)-(cηf1+af2-cf2-q0)·

cos(f0+φi)=0

(15)

对于管道释放点，θη(0)=f(0)+φi，结合式(11)，可得

同理，根据式(14)、(15)可得

(16)

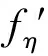
(17)

所以，在x=1处的内部解为

(18)

式中，

2.4 非线性微分方程的合成解

非线性微分方程在整个区域内(x∈[0,1])的合成解为

θ(x,ε)=θ0(x,ε)+θi(ξ,ε)+θi(η,ε)-

(19)

(20)

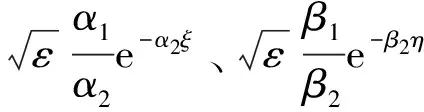
3 算例及结果验证

该部分计算选用管道外径为0.914 m，管道厚度0.127 m，水深1 000 m，张紧力189 t，每1m管道湿重和空气中质量分别为90 kg及980 kg，管道的弹性模量为207 GPa，海床斜度角为0°，管道入水角为85°，管道释放点在水面下2 m.

利用ABAQUS 6.12对文中的解析解进行验证.在非线性有限元模型中，管道采用B32梁单元，单元尺寸为10 m；海底采用S4R壳单元，单元尺寸为10 m.管道两端的边界条件如下：忽略铺管塔和海底的变形，将其约束为刚性面，为管道与海底设置接触.

图2给出了J-Lay铺管过程中奇异摄动法与有限元法求得的管道形态对比，其相关系数为0.991，这是高度吻合的.

图3将奇异摄动解与有限元解算出的管道弯矩进行对比，其相关系数为0.973，也验证了文中理论的正确性.

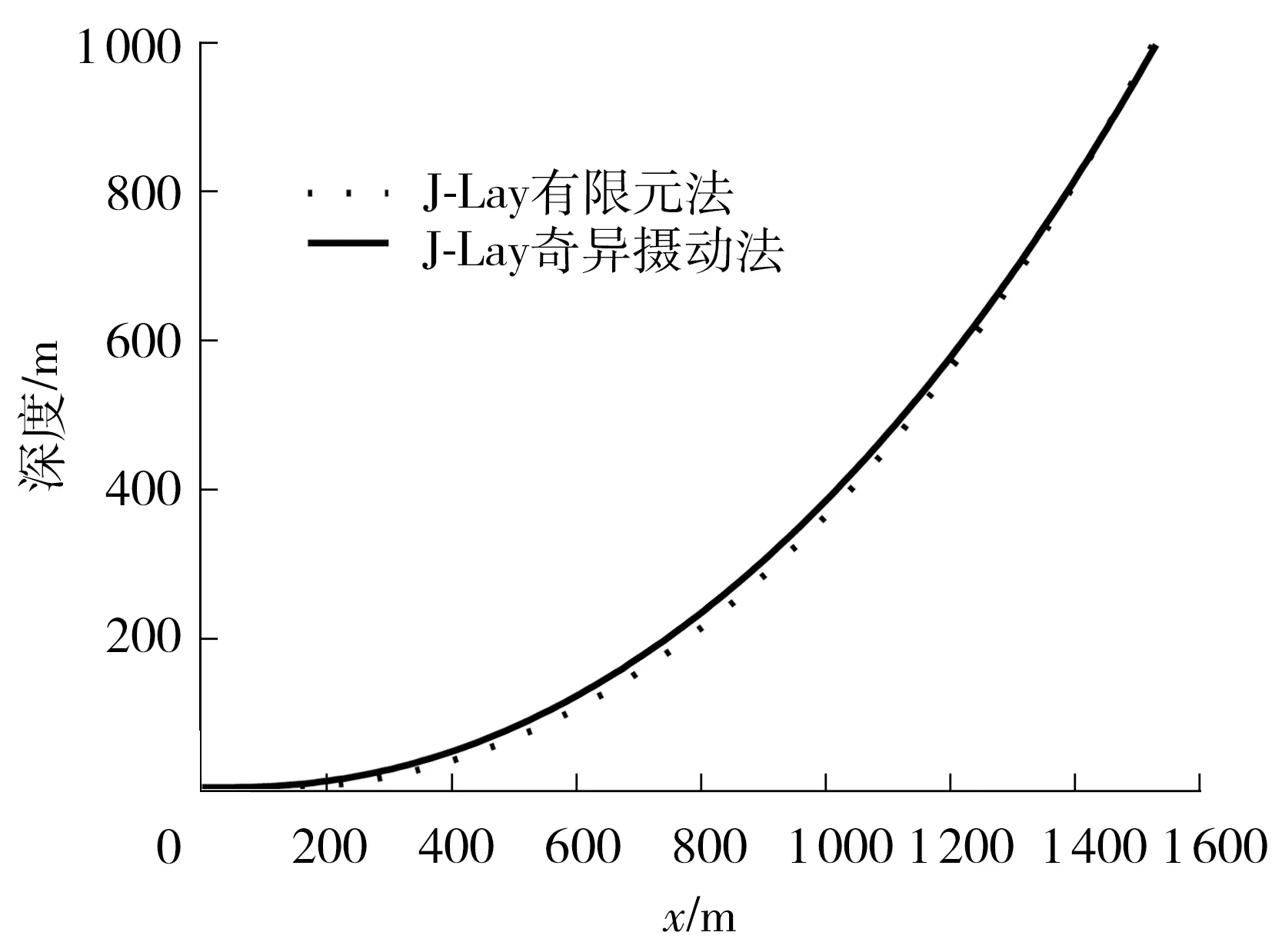
图2 J-Lay有限元解和奇异摄动解形态对比Fig.2 J-Lay geometric of different methods

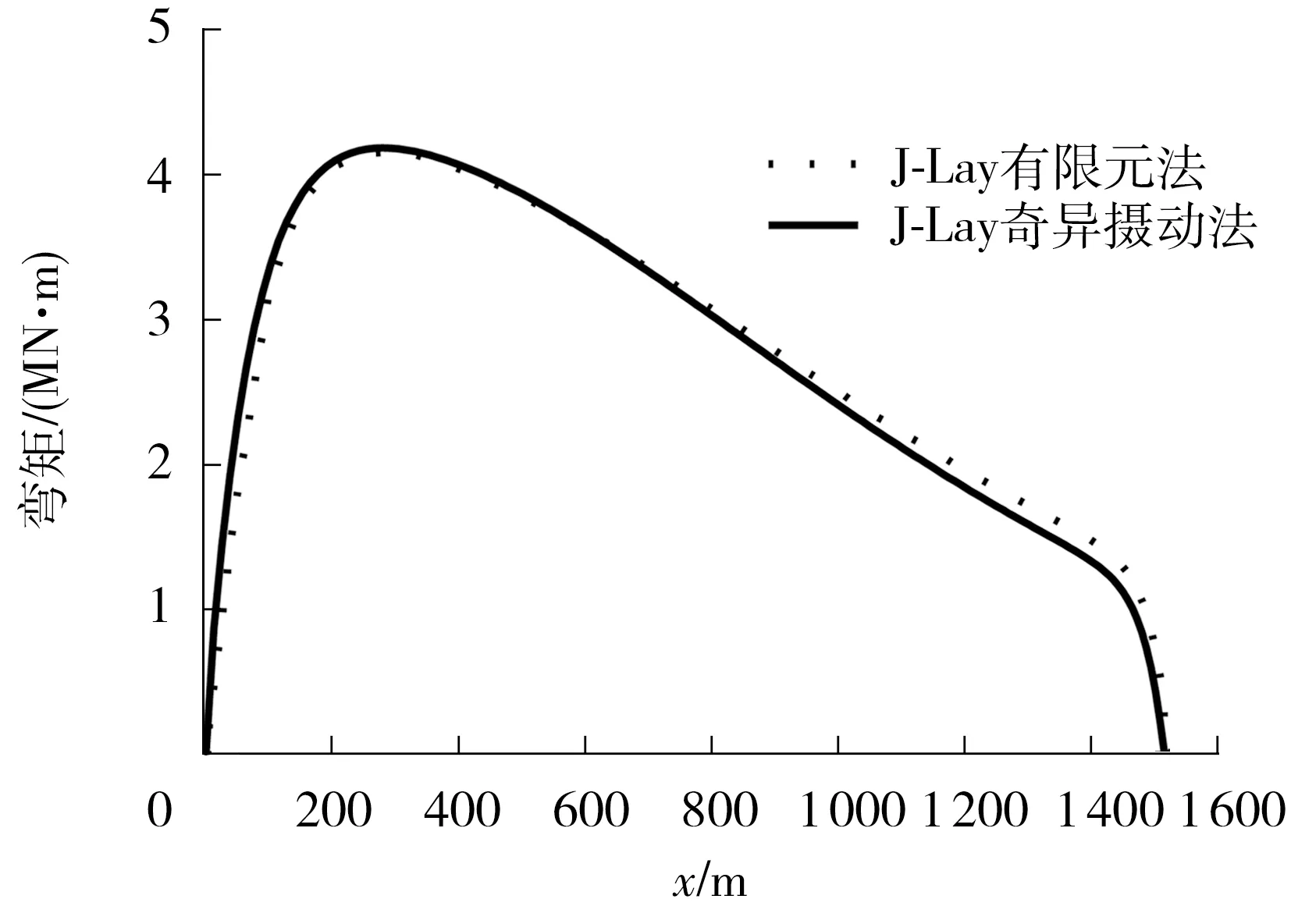
图3 J-Lay有限元解和奇异摄动解弯矩对比Fig.3 J-Lay bending moment of different methods

4 不同参数对J-Lay铺管的影响

J-Lay管道铺设涉及的参数非常之多，包括张紧力、水深、管道入水角、管道湿重、管道刚度、水流力等.由于铺管参数对管道的铺设具有极大的影响，文中利用推导出的奇异摄动解，重点研究了张紧力、水深和水流力变化对海底管道铺设的影响.

4.1 张紧力的影响

从图4可以看出，在其它铺管参数不变的情况下，在一定的范围内，张紧力越小，管道的形态越陡，管道释放点至TDP的水平距离越短，靠近TDP的管段弯矩峰值越大，对铺管越不利.所以，J-Lay铺管，在张紧器设计安全负荷范围内应适当增加张紧力，这样对铺管有利.

4.2 水深的影响

图5显示在其它铺管参数不变的情况下，当海水的深度为1 200 m时管道的形态比深度为1 000和1 400 m时都较为平缓，这说明管道的形态并不是随着水深的变化而单调的变陡或者变缓.

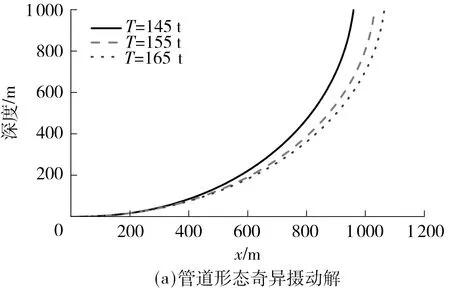
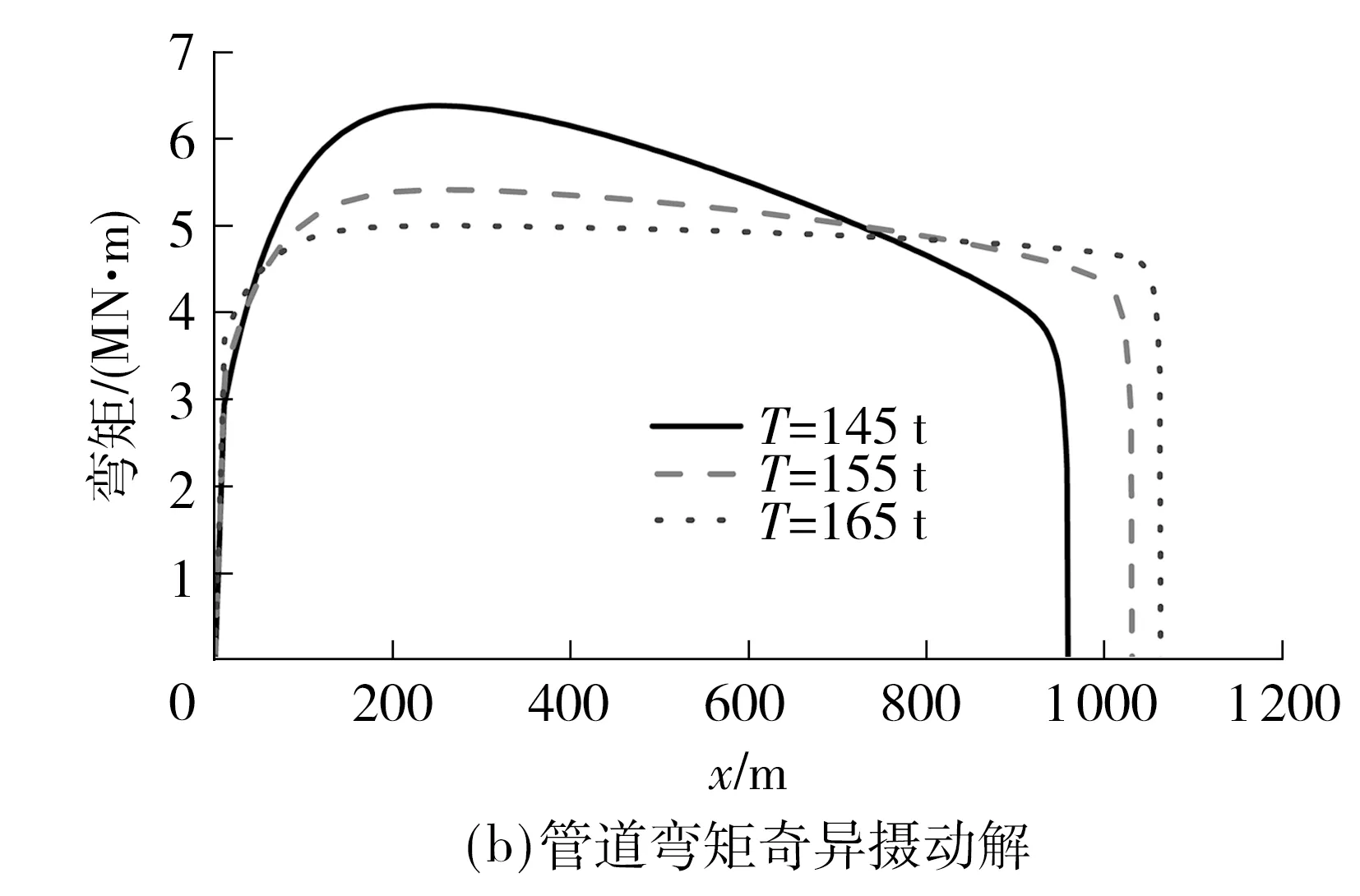
图4 不同张紧力下J-Lay管道的形态和弯矩Fig.4 Pipelines geometric and bending moment of J-Lay pipline at different tensions

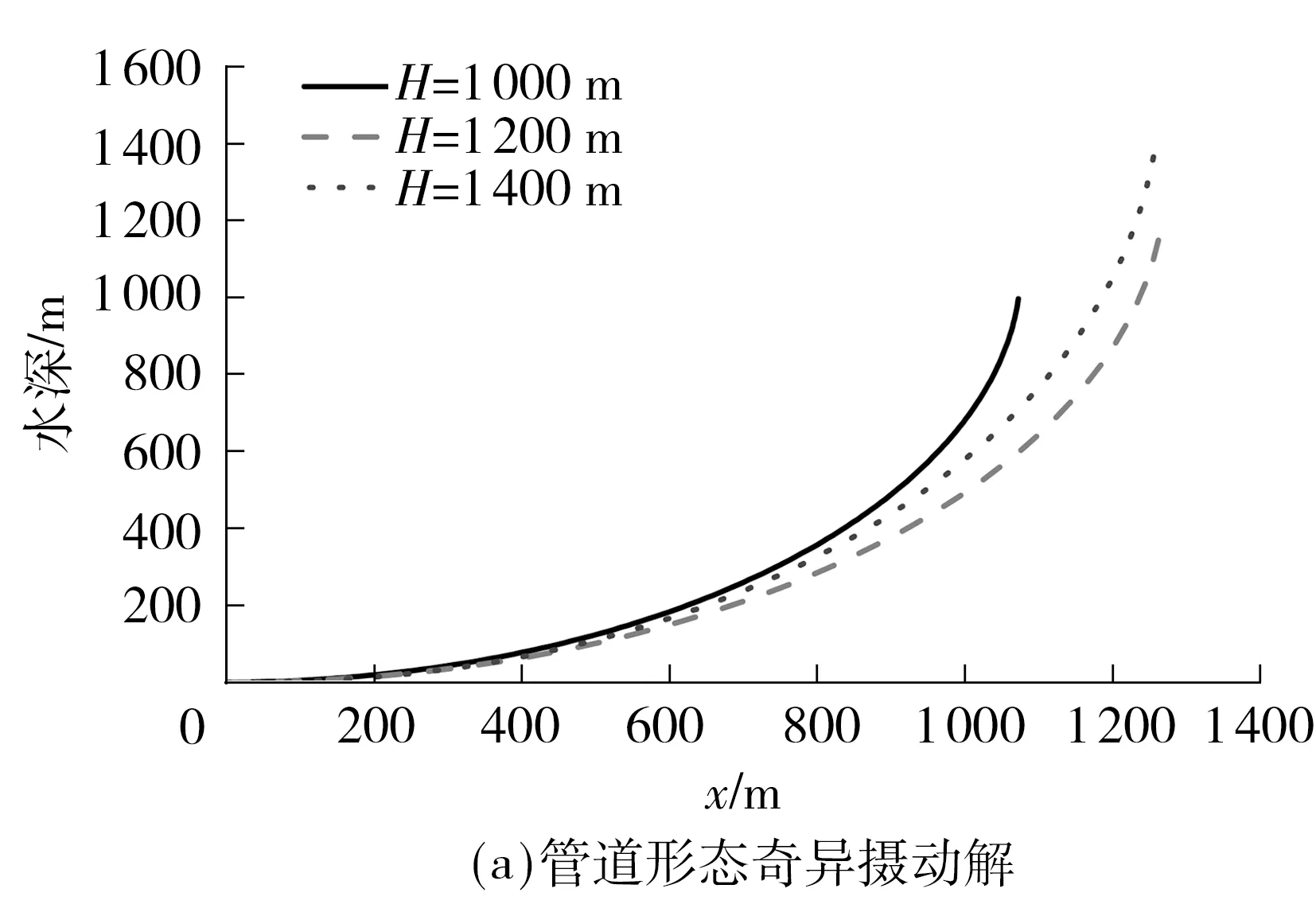
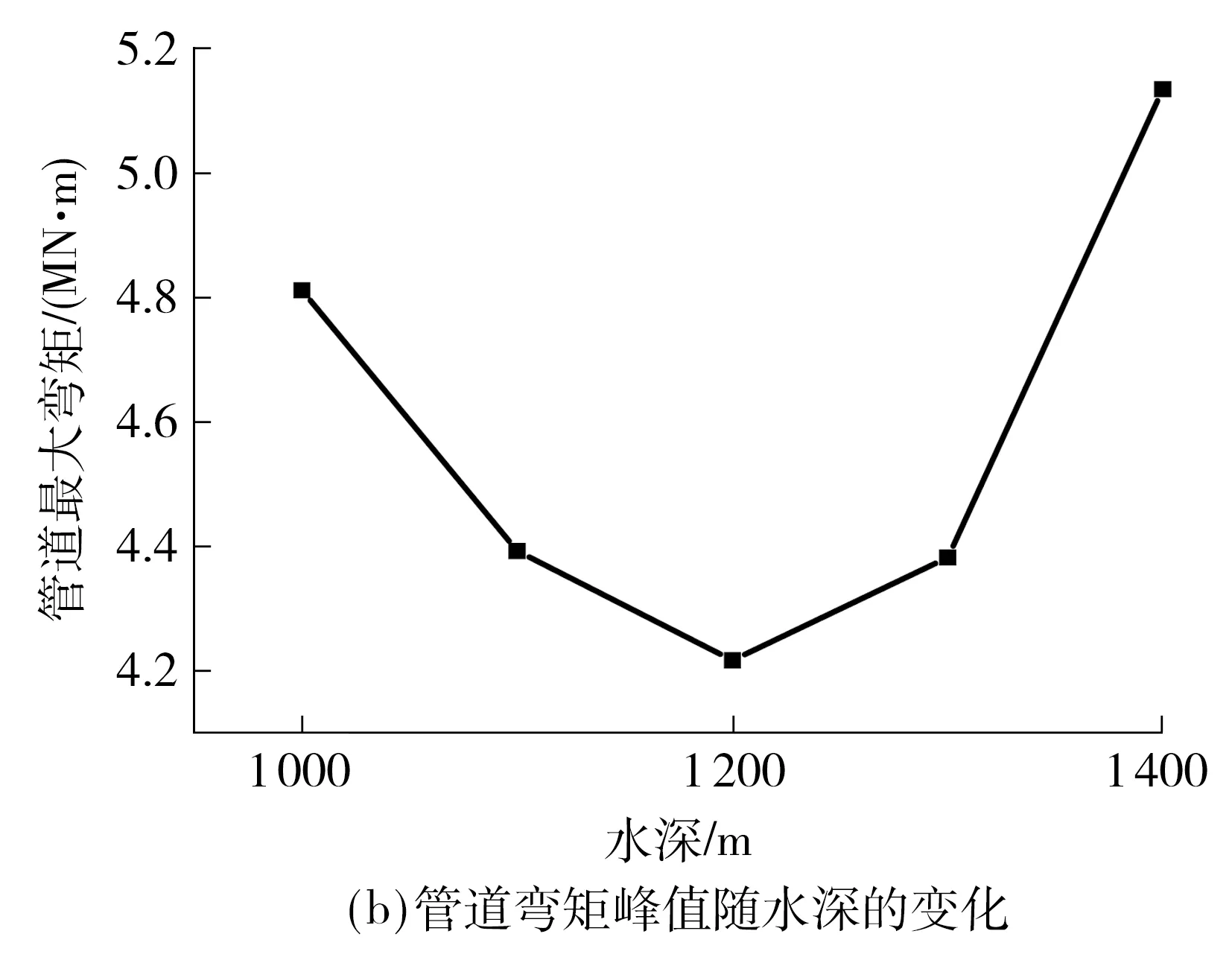
图5 不同水深下J-Lay管道的形态和弯矩Fig.5 Pipelines geometric and bending moment of J-Lay pipline at different depths

从图5(b)不难发现：当海水的深度为1 400 m时，管道的弯矩最大；深度为1 200 m时，管道的弯矩最小.管道的弯矩峰值不随水深的加大而单调变大或变小，而是中间有个拐点，这是因为J-Lay铺管法较适用于深水环境管道铺设，对特定的管道尺寸以及材质参数，当海水较浅时，管道转角在有限的水深内变化太大，导致管道曲率较大，弯矩也就较大；当海水深度加深时，管道的曲率会相应减小，应变也会随之减小；但是，随着海水深度的持续加大，海水深度达到一定值时，会导致靠近海底边界层区域的管道曲率变大，导致管道弯矩峰值变大.这与S-Lay管道有根本性的不同，因此在J-Lay铺管中须根据具体的参数对管道路由所覆盖的水深范围进行管道形态和弯矩等指标的数值分析.

4.3 水流力的影响

从图6可以看出，在其他铺管参数不变的情况下，当受到与铺管方向相反的水流力时，水流力越大，管道形态越陡，靠近海底部弯矩的峰值越大，对铺管越不利；当受到与铺管方向相同的水流力时，适当的水流力能减小管道的弯矩峰值.所以，在深水环境J-Lay铺管，应选择海况较好的时候，尽量避免逆流铺管.

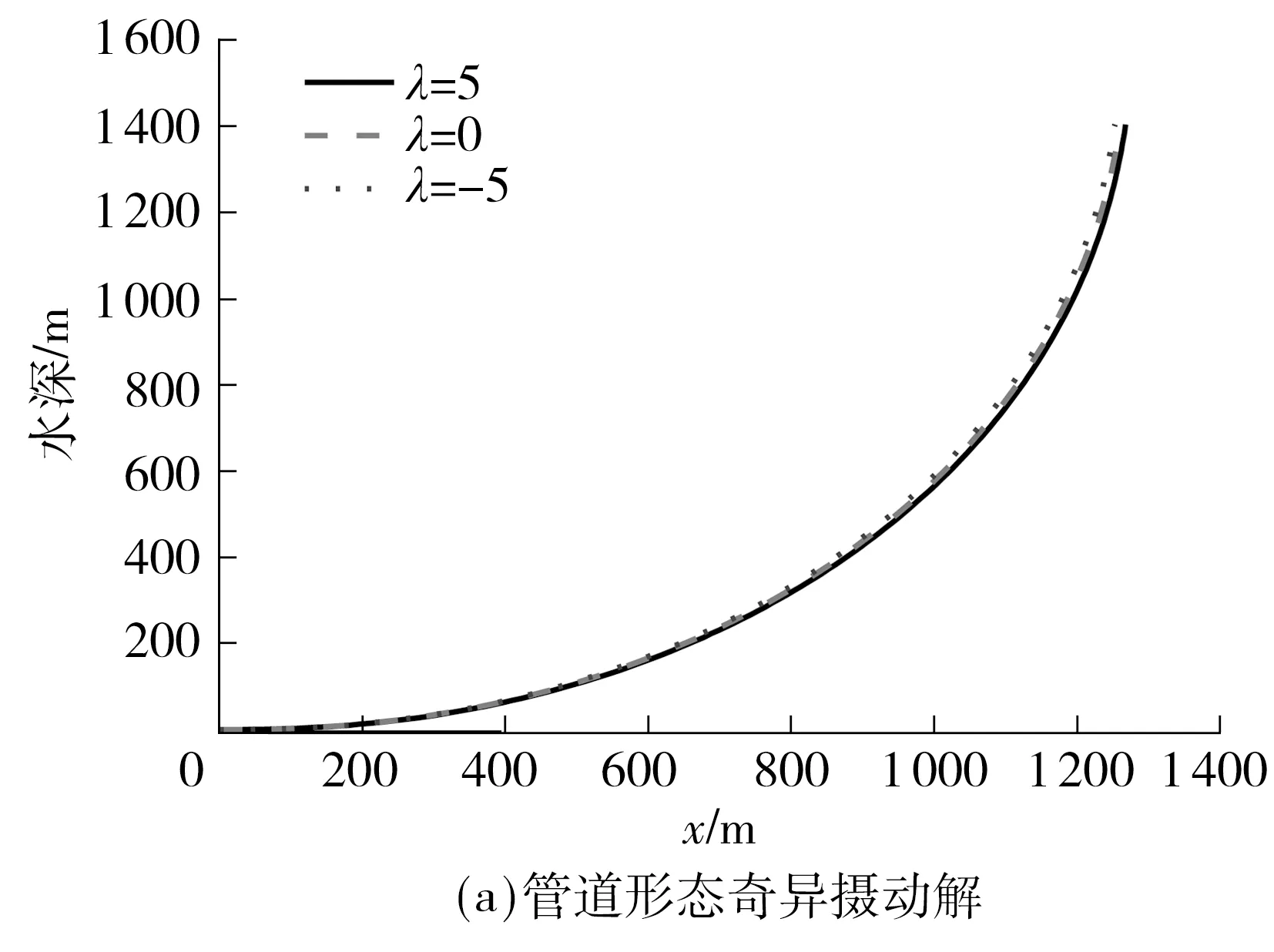
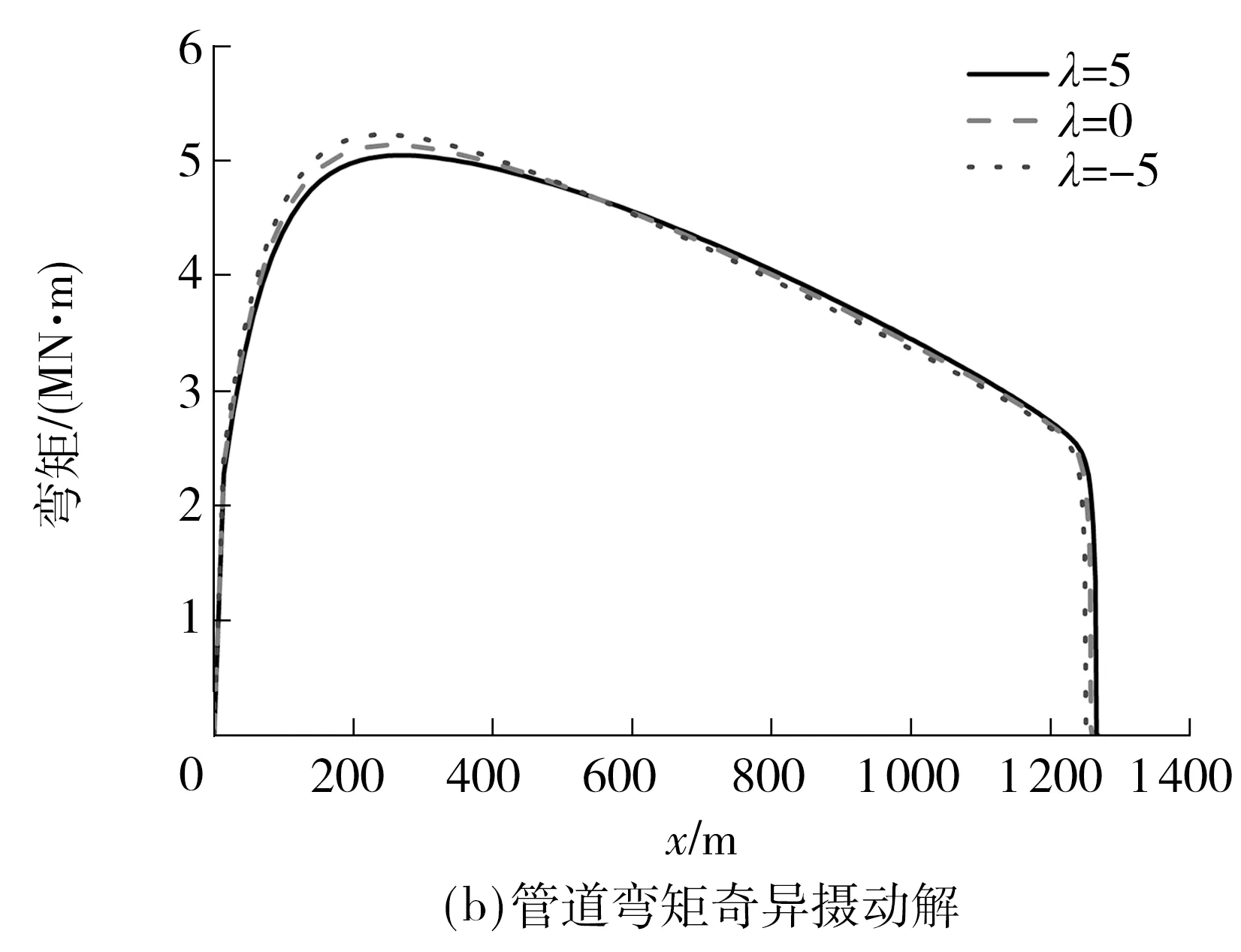
图6 不同水流力下管道的形态和弯矩Fig.6 Pipelines geometric and bending moment of pipline at different current forces

5 结论

文中针对深水环境J-Lay大直径薄壁管道铺设的非线性受力问题，推导出了管道的非线性微分方程，通过奇异摄动分析得到了管道形态的解析解，并研究了张紧力、水深以及水流力变化时对管道形态和弯矩的影响.通过与有限元数值解的对比，证明了文中理论的正确性.理论结果表明：J-Lay管道铺设过程中，其弯矩的峰值总是出现在TDP附近的管段；在一定的范围内增加张紧力，管道的形态越平缓，弯矩峰值越小，对铺管越有利；其他铺管参数不变时，随水深的增加管道弯矩峰值并不是单调的增加；水流力与铺管方向相反时会增加管道的弯矩峰值，对铺管不利.

[1] ROBERT O’Grady,ANNETTE Harte.Localised assessment of pipeline integrity during ultra-deep S-lay installation [J].Ocean Engineering,2013,68(1):27-37.

[2] 黄钰，王伟.动态分析在深水海底管道S型铺设中的研究与应用 [J].中国造船,2013(A01):11-16.

HUANG Yu,WANG Wei.Application of dynamic analysis in deepwater S-lay [J].Shipbuilding of China,2013(A01):11-16.

[3] 龚顺风,陈源,金伟良,等.深水海底管道s型铺设形态分析 [C]∥第十四届中国海洋(岸)工程学术讨论会论文集.呼和浩特:海洋出版社.2009:123-129.

[4] 朱达善,黄玉盈.海底管线用铰接式托架铺设时的大变形分析 [J].华中工学院学报,1986,14(3)：329-336.

ZHU DA-shan,HUANG Yu-ying.Large deflection of submerged pipelines laid with an articulated stinger [J].Journal of Huazhong University of Science and Technology,1986,14(3):329-336.

[5] 韩强，汪志钢，张永强，等.深海S-lay铺设大直径薄壁管道的奇异摄动分析 [J].华南理工大学学报(自然科学版),2015,43(6):116-121.

HAN Qiang,WANG Zhi-gang,ZHANG Yong-qiang,et al.Singular perturbation analysis of large-diameter and thin-wall pipeline during ultra-deep S-lay installation [J].Journal of South China University of Technology(Natural Science Edition),2015,43(6):116-121.

[6] 周巍伟，张恩勇，曹静.深水海底管道S型铺设影响因素分析 [J].中国海上油气,2016,28(2):145-150.

ZHOU Wei-wei,ZHANG En-yong,CAO Jing.Analysis of factors influencing deep water submarine pipeline S-lay operations [J].China Offshore Oil and Gas,2016,28(2):145-150.

[7] YUAN Feng,WANG Li-zhong,GUO Zhen,et al.Analytical analysis of pipeline-soil interaction during J-lay on a plastic seabed with bearing resistance proportional to depth [J].Applied Ocean Research,2012,36(3):60-68.

[8] HAN F，WANG DG，CAO J，et al.Research on design of the J-lay tower for deepwater pipe laying [J].Ocean Engineering,2012,30(1):126-130.

[9] LENCI S,CALLEGARI M.Simple analytical models for the J-lay problem [J].Acta Mechanica,2005,178(1/2):23-39.

[10] 康庄，张立，张翔.悬链线和大变形梁理论的J型铺设研究 [J].哈尔滨工程大学学报，2015，36(9):1170-1176.

KANG Zhuang,ZHANG Li,ZHANG Xiang.Analysis of J-Lay installation of a steel catenary riser based on catenary and large deflection beam theory [J].Journal of Harbin Engineering University,2015，36(9):1170-1176.

[11] WANG Qin,DUAN Meng-lan,LI Hai-ming,et al.A singular perturbation method for parametric investigation on J-lay installation of deepwater pipelines [J].Ocean Engineering,2013,27(6):751-766.

[12] BRAZIER L G.On the flexure of thin cylindrical shells and other thin sections [J].Proceeding of the Royal Society A,1927,116(773)：104-114.

[13] 黄玉盈,朱达善.海洋管线铺设时的静力分析 [J].海洋工程,1986,4(1)：32-46.

HUANG Yu-ying,ZHU Da-shan.Static analysis of submarine pipelines during installation [J].The Ocean Engineering,1986,4(1)：32-46.

[14] SPYROS A Karamanos.Bending instabilities of elastic tubes [J].International Journal of Solids and Stuctrues,2002,39(8):2059-2085.

[15] 刘书德，鲁世平，姚静荪，等.奇异摄动边界层和内层理论 [M].北京:科学出版社,2012.

Supported by the National Natural Science Foundation of China(11472108)

TheoreticalAnalysisandNumericalSimulationofLarge-DiameterandThin-WallPipelinesDuringUltra-DeepJ-LayInstallation

ZHANGYong-qiang1,2

(1.School of Civil Engineering and Transportation, South China University of Technology, Guangzhou 510640, Guangdong, China;2.Guangzhou Salvage, Guangzhou 510260, Guangdong, China)

In this paper, a nonlinear differential equation of pipelines is established by considering the BRAZIER effect. Then, the analytical solution to the J-Lay pipeline configuration is obtained through the singular perturbation theory, and such key parameters as the bending moment and the axial force of the pipeline are solved by means of the iterative method. Meanwhile, the analytical solution of the pipeline is proved to be correct by means of the finite element method. Finally, the influences of the tension, the water depth and the ocean currents on the configuration and bending moment of the J-Lay pipeline are investigated. Theoretical results show that (1) in the laying process of the J-Lay pipeline, the peak of the bending moment is always present in the pipeline section near the touch down point; (2) when the tension is increased in a certain range, the more smooth the pipeline configuration is, the smaller the peak value of the bending moment will be, which is beneficial to the pipeline laying; (3) when the other parameters are constant and the water depth increases, the increase of the bending moment peak value of the pipeline is not monotonous; and (4) when the current force is in the opposite direction of the pipe laying, the bending moment peak value of the pipeline increases, which is detrimental to the pipeline laying.

thin-wall pipeline; nonlinearity; singular perturbation; analytical solution; bending moments

2017-03-07

国家自然科学基金资助项目(11472108)

张永强(1975-),男,博士生,高级工程师,主要从事水工混凝土结构、钢结构及钢混结构研究.E-mail:zhangyq@gzsalvage.cn

1000-565X(2017)08-0126-06

O 39

10.3969/j.issn.1000-565X.2017.08.018