致密储层动态渗透率预测模型
董满仓, 柴汝宽, 辛 晶, 陈映赫, 黄建树
(1.延长油田股份有限公司, 陕西 延安 716000; 2.中国石油大学(北京) 石油工程教育部重点实验室,北京 102249)
0 引言
随着鄂尔多盆地等低渗致密油藏开发,其特殊的物性变化规律逐渐引起注意.其中以渗透率最为重要,储层状态不断改变,渗透率受到温度、有效应力和含水饱和度等多种因素的影响呈现非线性变化趋势.基于此,国内外学者[1-9]进行了一系列的研究.李卫东[1]、焦春艳[2]等,实验验证致密储层开发中有效应力的增加引起孔隙、喉道变形,造成储层渗透率下降.贺玉龙[4]、刘向君[5]等分析致密储层渗透率随温度的变化规律并建立相应函数关系.曾平[7]、游利军[8]等基于实验研究含水饱和度对储层渗透率的影响.有效应力、温度和含水饱和度等多种因素相互耦合导致渗透率的变化趋于随机性和模糊性,而现有产能模型[9,10]中渗透率要么取定值要么基于单一变量并不能真实表征渗透率的变化,导致产能模型存在较大误差,更为准确的渗透率预测方法有待建立.
BP神经网络具有很强的非线性动态处理能力,常用于解决实际生活中高度非线性、复杂性及模糊性的问题[11].但在实际应用中BP神经网络模型存在易陷入局部极值,收敛速度慢,网络结构的不确定性等问题[12].目前主要利用一些智能优化算法来优化BP神经网络[13-15].其中, Karaboga[16]于2005年提出人工蜂群算法能够较好优化BP神经网络.利用人工蜂群算法获取最优个体对 BP神经网络的初始权值和阈值进行优化,能够较大程度的改善BP神经网络模型预测的准确性,具有较高的实用价值[17,18].
为准确描述致密油藏开发过程中渗透率动态变化规律,本文首先分析总结了致密储层渗透率的三个主要影响因素:有效应力、温度和含水饱和度.然后,将有效应力、温度和含水饱和度作为输入层,渗透率作为输出层,建立BP神经网络预测模型并利用人工蜂群算法优化BP 神经网络初始权值和阈值,训练模型并进行预测.基于文献[7]中的研究数据,应用人工蜂群算法优化BP神经网络的致密油藏渗透率预测模型的实用性和准确性.本文模型可以应用于产能模型构建及数值模拟中渗透率表征,具有良好的应用前景.
1 致密储层渗透率影响因素
致密砂岩储层物性整体较差,储集空间以剩余原生粒间孔隙和溶蚀孔隙为主,孔隙结构类型属小孔-微细喉道型,储层颗粒粒度细小,杂基和胶结物含量高,储层压实和胶结作用强,岩石致密孔隙度、渗透率低.同时,致密储层的特殊物性条件造成渗透率影响因素极为复杂,除了沉积环境、孔喉结构等还受到开发过程中各种因素的影响,其中以温度、有效应力和含水饱和度三者为主.
1.1 有效应力对致密储层渗透率的影响
当储层温度和含水饱和度一定时,有效应力对于致密储层渗透率的影响机理为[2,3]:
(1)随着有效应力的增大,致密储层进一步被压实,孔隙、喉道受压变形,流体渗流通道越来越小,渗透率越来越低.尤其是致密储层中喉道的受力闭合,导致渗透率大幅度的降低.
(2)当储层被压缩到一定程度以后,岩石颗粒受力趋于平衡,有效应力对孔隙、喉道的压缩效应逐渐变小,孔隙、喉道大小趋于稳定,储层渗透率也趋于稳定.
1.2 温度对致密储层渗透率的影响
当储层有效应力和含水饱和度保持不变时,温度变化(本文数据涉及最高实验温度为60 ℃,远低于门槛温度,不足以出现高温下岩样受热开裂导致渗透率剧增的现象)对低渗致密油藏渗透率影响机理为[4-6]:
(1)随着温度的升高,岩石骨架颗粒受热膨胀,直接压缩孔隙、喉道,造成流体渗流通道减小,储层渗透率下降.此外,不同矿物热膨胀系数不同导致岩石颗粒膨胀的非均质性极易造成流体渗流通道迂曲度的增加,极大增加渗流阻力,进而影响渗透率.
(2)随着温度升高,岩石的刚度和强度均降低,屈服应力降低,使岩石易在应力作用下产生形变,压缩流体渗流通道,降低储层的渗透能力.
(3)随着温度升高,致密储层中黏土矿物的分散加剧,分散后黏土颗粒堵塞孔隙、喉道造成渗透率的下降.
1.3 含水饱和度对致密储层渗透率的影响
当储层有效应力和温度一定时,含水饱和度对致密储层渗透率的影响机理为[7-9]:
(1)随着含水饱和度的增加,水分子进入岩石颗粒粒间孔隙润滑颗粒,软化岩石使岩石的抗压强度降低导致岩石更易受力变形,进而易引起储层岩石渗透率的降低.
(2)含水饱和度的增加,加速岩石中黏土矿物(伊利石)的水化分散速率,分散后黏土微粒随着流体运移堵塞孔隙、喉道,降低储层渗透率;同时,水的注入易导致岩石中黏土矿物(蒙皂石)吸水膨胀,圧缩流体渗流通道,降低储层渗透率.
2 人工蜂群算法优化BP神经网络
2.1 BP神经网络结构
BP神经网络是指基于误差反向传播算法(Back Propagation,简称 BP 算法)的多层前向神经网络,无需获取输入与输出之间的函数关系,通过从样本数据中提取各输入与输出的隐式非线性对应关系实现高度的非线性映射[11,12].本文应用Matlab软件编写程序,采用3层BP神经网络,输入层为有效应力、温度和含水饱和度,输出层为储层渗透率.同时,利用人工蜂群算法优化BP神经网络的权值和阈值,建立人工蜂群算法优化BP神经网络的渗透率预测模型.BP神经网络结构,如图1所示.

图1 渗透率预测模型神经网络结构图
2.2 人工蜂群算法原理
在人工蜂群算法[17]中,将蜂群分为引领蜂、跟随蜂和侦察蜂3类,其中引领蜂和跟随蜂各占蜂群的一半,数量等于蜜源的数量,且每个蜜源同一时间内只有一只引领蜂采蜜.人工蜂群算法生成N个解决方案(食物源位置),N同样代表群体的大小,每个解决方案由式(1) 计算:
(1)
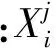
(2)
式(2)中:fi是解决方案i的目标函数.若新食物源的适应度大于前一个食物源,则蜜蜂会存储新的食物源位置信息,并且遗忘旧的食物源位置信息.反之,蜜蜂会保持记忆旧的食物源位置信息.当所有的引领蜂完成搜索过程后,在舞蹈区和跟随蜂分享食物源的蜂蜜量和位置信息.跟随蜂评价所有引领蜂带来的食物源信息并且根据适应度值得大小确定一个食物源.概率函数值Pi为:

(3)
式(3)中:fiti为位置i的适应度值,与食物源的花蜜量成正比.为了从旧的食物源位置中选择一个食物源位置,引领蜂和跟随蜂计算新食物源位置,如式(4)所示.
Vij=Xij+φij×(Xij-Xkj)
(4)
式(4)中:随机产生k={1,2,…,N}和j={1,2,…,D}.φij为[-1,1]中的随机数.随着Xij-Xkj值的增加,在位置Xij周围的搜索也会增加.随着搜索位置越来越接近最优解,步骤自适应降低.
2.3 人工蜂群算法优化BP神经网络基本思路
人工蜂群算法在多变量函数问题上具有较强优化能力,所以笔者选用人工蜂群算法优化BP神经网络,以建立更加稳定和准确的改进的BP神经网络.基本思路:在BP神经网络初始化阶段,把BP神经网络的权值和阈值即有效应力、温度和含水饱和对渗透率的影响程度作为人工蜂群算法的优化目标,选取BP神经网络的误差作为人工蜂群算法的适应度来评价和优选BP神经网络的权值和阈值.当人工蜂群算法迭代运行到最大迭代次数时,选择适应度最佳的一组权值和阈值用于BP神经网络训练[18],如图2所示.改进的BP神经网络将人工蜂群算法和BP神经网络二者的优点相结合,更加准确的应用于致密储层渗透率动态模型的建立.
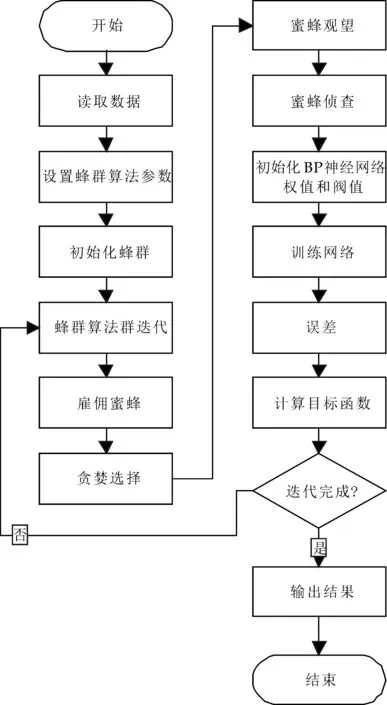
图2 基于人工蜂群优化的BP神经网络算法流程
3 实例验证
3.1 样本数据
基于前文研究,考虑有效应力、温度和含水饱和度对低渗致密储层渗透率的影响,选取文献[7]中分别对应不同的有效应力、温度和含水饱和度的26组实验数据建立学习样本(表1) .为检验模型的精度,最后4个数据作为检验样本不参加学习.

表1 致密油藏渗透率学习样本基础数据
续表1
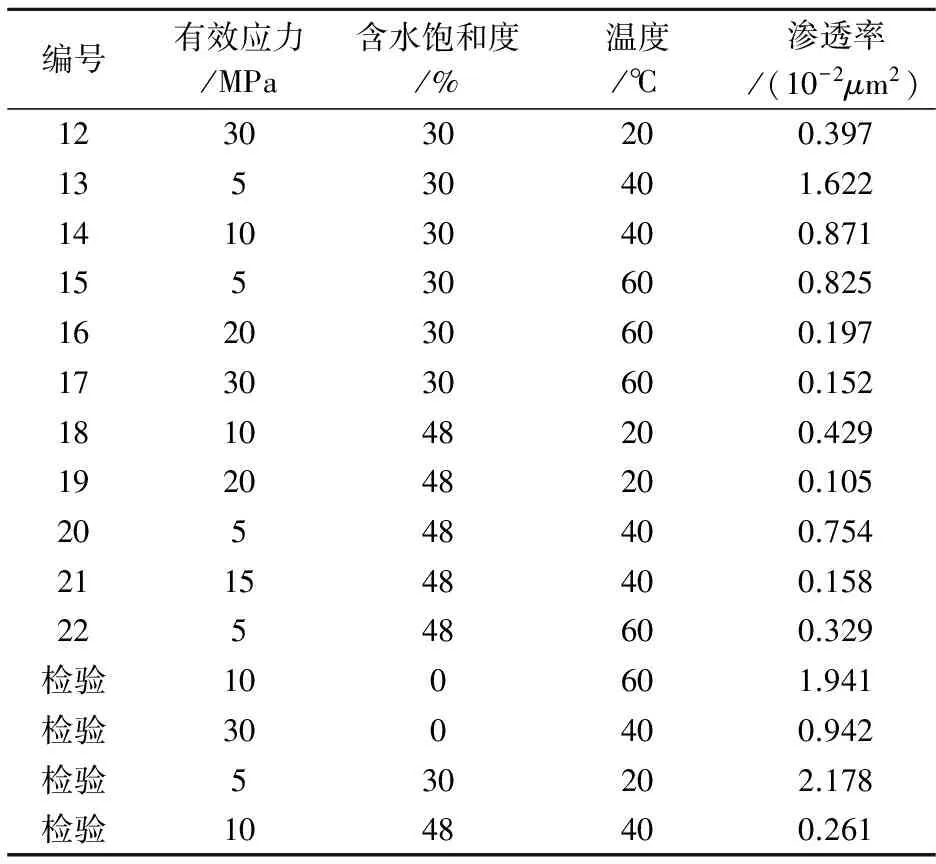
编号有效应力/MPa含水饱和度/%温度/℃渗透率/(10-2μm2)123030200.39713530401.622141030400.87115530600.825162030600.197173030600.152181048200.429192048200.10520548400.754211548400.15822548600.329检验100601.941检验300400.942检验530202.178检验1048400.261
3.2 样本训练及预测结果
将表1中1-22样本数据作为学习输入,渗透率作为目标输出进行学习训练,最后4组数据用于检验预测模型的准确性.训练和预测结果如表2所示:人工蜂群算法优化的BP神经网络模型训练结果的最大绝对误差为0.063 47×10-3μm2,最大相对误差为4.382%.验证结果最大绝对误差为0.013 37×10-3μm2,最大相对误差为2.245%.说明基于人工蜂群算法优化的BP神经网络模型能够很好的描述致密储层岩石渗透率与有效应力、温度和含水饱和度等影响因素之间的内在联系与规律,即模型能够较好应用于致密储层渗透率预测.

表2 人工蜂群算法优化BP神经网络预测结果与实测值对比
续表2

编号实际值/(10-2μm2)预测值/(10-2μm2)绝对误差/(10-2μm2)相对误差/%190.1050.10630.001341.274200.7540.7409-0.01306-1.732210.1580.1577-0.00025-0.159220.3290.3247-0.00431-1.310检验1.9411.94380.002810.145检验0.9420.95540.013371.419检验2.1782.1656-0.01243-0.571检验0.2610.2551-0.00586-2.245
3.3 验证结果与分析
基于未训练的原始实验数据[7],应用人工蜂群算法优化的BP神经网络渗透率模型进行渗透率预测与实际值相对比验证模型的准确性并分析各影响因素的作用机理.
图3为储层温度和含水饱和度一定时,改变储层有效应力得到的致密储层渗透率-有效应力关系曲线.随着有效应力的增加,渗透率逐渐下降,但下降速率逐渐减小.因为随着有效应力的增大,致密储层被进一步压实,孔隙、喉道受压变形,流体渗流通道逐渐变小,渗透率逐渐降低.但当储层被压缩到一定程度,岩石颗粒受力趋于平衡,有效应力对孔隙、喉道的压缩效应逐渐变小,孔隙、喉道大小趋于稳定,储层渗透率趋于稳定.如图3可知,预测结果较好地贴合了实测值.
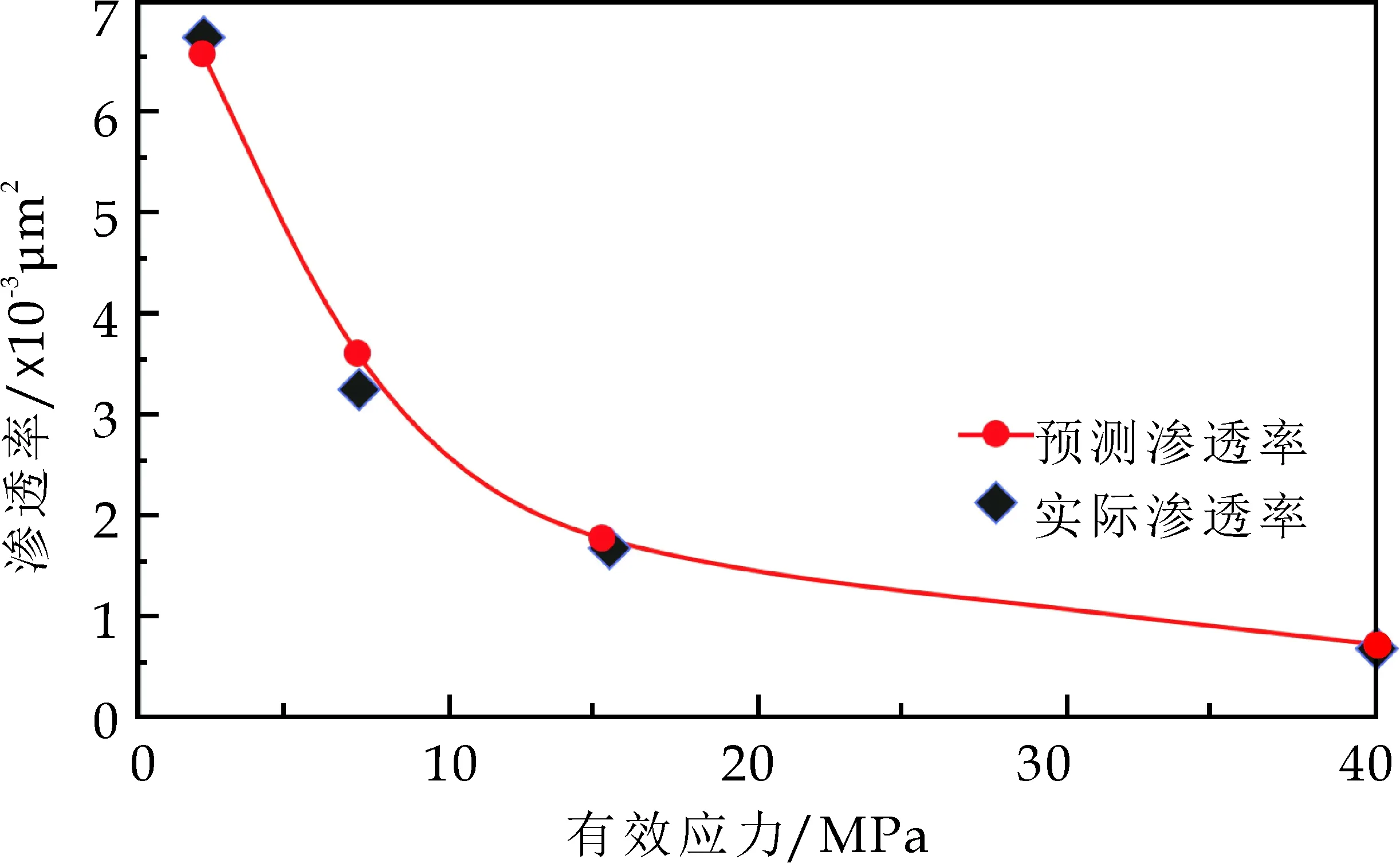
图3 有效应力-渗透率曲线
图4为储层有效应力和含水饱和度一定时,改变储层温度得到的致密储层渗透率-温度关系曲线.随着温度的升高,致密储层渗透率逐渐降低.因为随着温度的升高,岩石骨架颗粒受热膨胀,直接压缩孔隙、喉道,造成流体渗流通道减小,储层渗透率下降.此外,不同矿物热膨胀系数不同导致岩石颗粒膨胀的非均质性极易造成流体渗流通道迂曲度的增加,增加渗流阻力.
图5为储层温度一定时,改变储层含水饱和度得到的致密储层渗透率-有效应力关系曲线.随着含水饱和度的增加,渗透率逐渐下降.因为随着含水饱和度的增加,岩石中黏土矿物(伊利石)的水化分散速率增加,分散后黏土微粒随着流体运移堵塞孔隙、喉道,造成储层渗透率的降低;同时,水的注入易导致岩石中黏土矿物(蒙皂石)吸水膨胀,压缩流体渗流通道,引起储层渗透率的降低.由图5可知,预测结果较好地贴合了实测值.
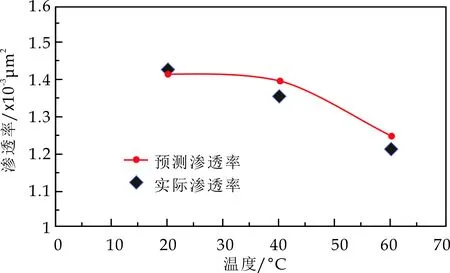
图4 温度-渗透率曲线

图5 不同含水饱和度下渗透率变化曲线
3.4 与常规BP神经网络结果对比
基于表1样本数据,应用常规BP神经网络模型进行学习训练.由图6可知,人工蜂群算法优化BP网络模型的训练误差相对稳定,最大相对误差4.382%,平均相对误差1.069%,较之常规BP神经模型的最大相对误差24.703%,平均误差10.699%,训练结果精度和稳定性均有较大改善.所以,人工蜂群算法能够合理的优化BP神经网络的权值和阈值.即人工蜂群算法和BP神经网络组成的改进的BP神经网络模型对低渗致密油藏渗透率预测具有较好的适应性.
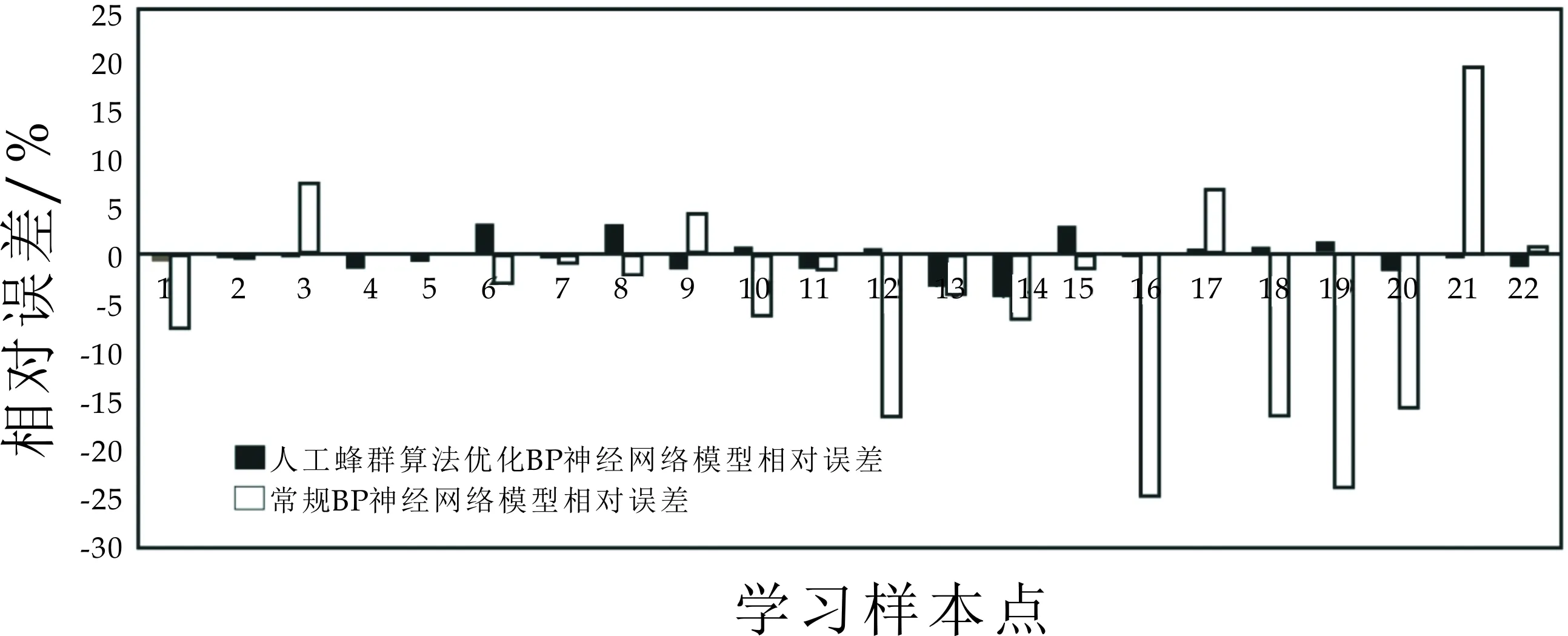
图6 改进、常规BP神经网络模型相对误差对比图
4 结论
(1)分析总结了有效应力、温度和含水饱和度对致密储层渗透率的影响,并建立了以有效应力、温度和含水饱和度为输入层,渗透率为输出层并应用人工蜂群算法优化BP神经网络权值和阈值的渗透率预测模型.
(2)人工蜂群算法优化的BP神经网络模型所得训练结果的最大绝对误差为0.063 47×10-3μm2,最大相对误差为4.382%,预测值接近实测值.说明该改进的BP神经网络模型能够较为准确描述致密储层渗透率与温度、有效压力和含水饱和度等因素之间的内在联系.
(3)常规BP模型训练结果的最大相对误差24.703%,平均误差10.699%,远大于人工蜂群算法优化的BP神经网络模型,说明人工蜂群算法优化的BP神经网络相比于常规BP神经网络预测精度及稳定性均有较大提升,该改进的BP神经网络模型对鄂尔多斯盆地等特殊低渗致密储层的渗透率预测具有较好的适应性.
[1] 李卫东,吴亚芳,马 哲,等.考虑渗透率变化的低渗透油藏非达西渗流模型[J].陕西科技大学学报(自然科学版),2015,33(2):111-115.
[2] 焦春艳,何顺利,谢 全,等.超致密砂岩储层应力敏感性试验[J].石油学报,2011,32(3):489-494.
[3] 肖文联,李 闽,赵金洲,等.致密砂岩渗透率应力敏感性试验研究[J].岩土力学,2010,31(3):775-779.
[4] 贺玉龙,杨立中.温度和有效应力对砂岩渗透率的影响机理研究[J].岩石力学与工程学报,2005,24(14):2 420-2 427.
[5] 刘向君,高 涵,梁利喜.温度围压对致密砂岩孔隙度和渗透率的影响研究[J].岩石力学与工程学报,2011,30(S2):3 771-3 778.
[6] 梁 冰,高红梅,兰永伟.岩石渗透率与温度关系的理论分析和试验研究[J].岩石力学与工程学报,2005,24(12):2 009-2 012.
[7] 曾 平,赵金洲,李治平,等.温度、有效应力和含水饱和度对致密砂岩渗透率影响的实验研究[J].天然气地球科学,2005,16(1):31-34.
[8] 游利军,康毅力,陈一健,等.含水饱和度和有效应力对致密砂岩有效渗透率的影响[J].天然气工业,2004,24(12):105-107.
[9] 方思冬,战剑飞,黄世军,等.致密油藏多角度裂缝压裂水平井产能计算方法[J].油气地质与采收率,2015,22(3):84-89.
[10] Civan F,Rai C S,Sondergeld C H.Shale-gas permeability and diffusivity inferred by improved formulation of relevant retention and transport mechanisms[J].Transport in Porous Media,2011,86(3):925-944.
[11] 陈 桦,程云艳.BP神经网络算法的改进及在Matlab中的实现[J].陕西科技大学学报(自然科学版),2004,22(2):45-47.
[12] 程 玥.BP神经网络的算法改进与应用研究[D].重庆: 重庆大学,2011.
[13] 田 冷,何顺利,顾岱鸿,等.改进BP神经网络模型在长庆气田产能预测中的应用[J].石油天然气学报,2008,30(5):106-109.
[14] 尹光志,李铭辉,李文璞,等.基于改进BP神经网络的煤体瓦斯渗透率预测模型[J].煤炭学报,2013,38(7):1 179-1 184.
[15] 江文荣,张 科.径向基函数神经网络在孔隙度预测中的应用[J].中国海上油气,2008,20(5),305-307.
[16] Karaboga D.An idea based on honey bee swarm for numerical optimization[D].Kayseri:Erciyes University,2005.
[17] 王艳娇.人工蜂群算法的研究与应用[D].哈尔滨:哈尔滨工程大学,2013.
[18] 秦全德,程 适,李 丽,等.人工蜂群算法研究综述[J].智能系统学报,2014,9(2):127-135.

