意想不到的反转

刘金龙

数学最吸引人的地方，有时候是因为它“难”，“难”到实际情况与表面现象不符，甚至完全相反。正是这样的情况让人不由得想要开动脑筋，一探究竟。

录取比例引发的争议

学校新开设了一个艺术社团，同学们纷纷踊跃报名，以致于报名人数远远超出了社团所能容纳的人数。于是，社团采取了选拔录取的方式来控制入社人数。

选拔结束后，团长葛丽丽拿着名单慌慌张张地来到校长办公室：“校长，不好了，不好了！”

校长知道葛丽丽平时处事很稳重，诧异地问道：“怎么了？出什么事了？”

葛丽丽报告说：“男生说我们的社团选拔本来挺好的，让有特长的同学能更好地学习、发挥，可他们不能容忍社团的性别歧视行为。”

校长更惊诧了，学校可是公平对待每位学生的，怎么可能会出现这种情况？

“性别歧视？怎么说？”

葛丽丽继续说道：“某位数学尖子生看了社团的录取名单公示后，说我们社团有性别歧视，女生的录取率是男生的2倍。我们一算，还真是这样。”

校长虽然不解，但是对这个录取情况更感兴趣了：“哦，还有这样的情况？我们可是公平、公开、公正地选拔。你把录取情况拿给我看看。”

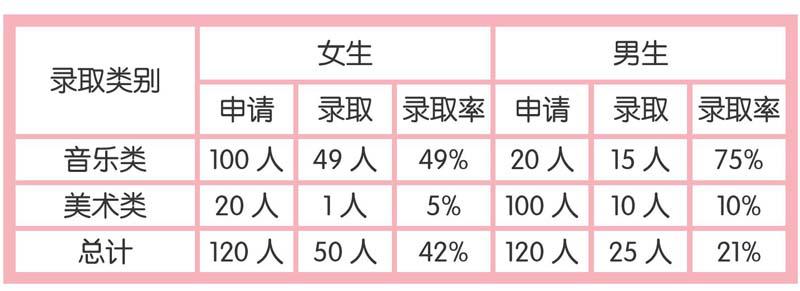
葛丽丽将社团录取情况统计表递给校长。

校长笑着夸奖葛丽丽：“你办事还真是细心，这份表格一目了然！”

“谢谢校长夸奖！女生的录取率是42%，而男生的录取率仅有21%，这样对男生好像确实不公平。”葛丽丽大着胆子说。

校长听完后哈哈大笑：“你们啊，都被那位同学带到了一个误区，走进了一个悖论里。”

葛丽丽听得一头雾水，却又看不出这里有什么不对。

我看社团确实存在性别歧视，录取的女生明显比男生多。

别这么轻易下结论，学校对待每位学生都是公平的，哪有什么性别歧视，且听听校长怎么说吧。

哪支球队实力更强

校长召集大家开会的消息传开了。听说要解释社团男女生录取比例的问题，那些未被选上的学生，尤其是男生，早早来到操场，都想听听校长怎么说。

看着黑压压的一大片学生，校长说道：“同学们，大家对艺术的热忱，我都看到了。今天我想给大家讲个故事。”人群中一阵骚动，不是说给大家解释社团招新的事吗？怎么变成讲故事了？

校长缓缓地说道：“故事讲完后，我有个问题需要大家和我一起探讨。”

一听到要和校长一起探讨问题，大家都安静了下来。

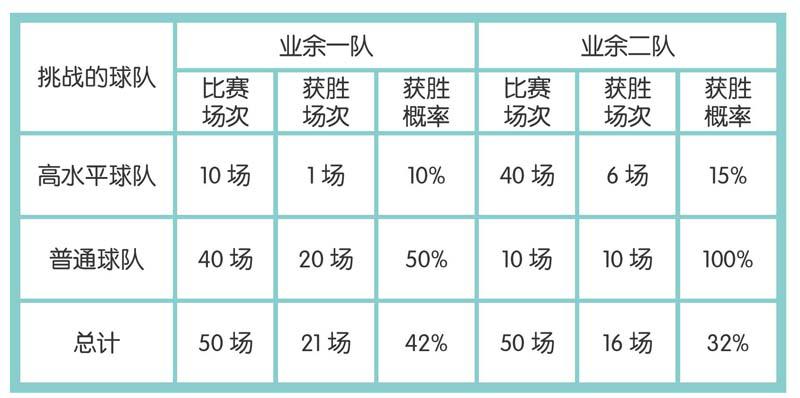
“曾经，几位篮球业余爱好者临时组建了一支籃球队，他们想知道自己的实力，于是决定和专业的篮球队进行50场比赛。他们先与高水平球队比赛10场，只胜了1场。随后，他们又与普通球队比赛40场，结果胜了20场。所以，他们总的获胜概率是42%，成绩好像还不错。”

听到这儿，有人提问了：“如果他们一开始就挑战普通球队，总的获胜概率会不会更高？”

“可是，当他们挑战高水平球队时，他们会输得很惨吧！”

校长笑了笑，示意大家安静，继续说：“这时候，又有另一支业余篮球队组建起来了。他们同样先挑战了高水平球队，连续比赛了40场，胜了6场。随后，他们挑战了普通球队，赛了10场，全胜。所以，他们总的获胜概率是32%。”

“他们挑战普通球队时是全胜啊，怎么会这样？”

“是啊，看他们跟高水平球队比赛的情况，也不比第一支球队差。”

“同学们，你们当中有很多是篮球爱好者，数学也很棒。大家觉得这两支业余球队，谁更厉害？”校长提问。

“看数据，第一支球队总的获胜率更高。”

“我感觉第二支球队的水平更高。”

“第二支球队更厉害啊，都完胜普通球队了。”

这是怎么回事？明明感觉是第二支球队更厉害，可统计数据却显示第一支球队的获胜概率更高。

和他们比赛的球队不是都有水平层级吗？条件不一样得出的结论当然不一样了。你要好好思考，不可光看这个笼统的统计结果。

听完大家的议论，校长说道：“按数据显示，确实是第一支球队总的获胜概率要高一些，可光凭这个数据就判定两支球队的水平，显然是不行的。很明显，第二支球队的实力要高于第一支球队。大家看，第一支球队与高水平球队打的场次少，与普通球队打的场次多，所以胜的总场次多。但其实他们与高水平球队打时获胜概率是10%，与普通球队打时获胜概率是50%。而第二支球队与高水平球队打的场次多，与普通球队打的场次少，他们的获胜概率：前者达到15%，后者达到100%。显而易见，第二支球队的实力要远远高于第一支球队。”

“感觉这个数据和社团的录取情况统计数据有些相似！”葛丽丽突然醒悟道。

“你们发现了吗？在社团招新中，音乐类和美术类的录取率相差很大，音乐类的录取率很高，而美术类的很低，同时男生女生的申请者分布比重相反。其中申请音乐类的男生录取率为75%，远远大于女生。美术类的录取率虽然都偏低，但男生的录取率同样高于女生，所以我们切不可将两者进行简单地直接汇总，否则大家就掉入一个辛普森悖论的陷阱里了。”校长笑着对大家说道。

哇！部分和整体竟然有这么大的差别，真是不可用量来衡量质啊！

终于明白了吧！以后可要好好学数学，别再闹出大笑话了。简单直接汇总分组数据，是不能反映真实情况的。为了避免辛普森悖论的出现，我们可以根据重要程度让各分组数据乘以一个分数。如果两组数据同等重要，那么它们都乘以1/2，否则所乘分数将不同，但两个分数之和为1，以此消除各分组数据差异所造成的影响。