危岩稳定性断裂力学分析方法浅析

(重庆交通大学河海学院 重庆 400074)

危岩稳定性断裂力学分析方法浅析

吴鹏飞

(重庆交通大学河海学院重庆400074)

危岩是山区比较常见的地质灾害。危岩失稳破坏的本质是岩体主控结构面在荷载组合的作用下发生扩展断裂。本文结合断裂力学的相关理论，总结前人的研究成果，重点运用断裂力学方法分析了重庆某危岩，计算了该危岩主控结构面的应力强度因子并以此为依据计算其稳定系数。分析结果与现实相符，证明了用断裂力学的方法分析危岩稳定性的可行性。

危岩；断裂力学；主控结构面；应力强度因子

一、前言

危岩指的是由多组岩体结构面切割并位于陡坡或陡崖上的不稳定岩体[1]，是西南地区比较常见的地质灾害类型之一。根据失稳模式，陈洪凯将危岩划分为坠落式、倾倒式和滑塌式危岩三种类型[2]。危岩的发育本质上是边坡上的岩体在各种荷载作用下，裂隙不断积累加剧，不断扩展，并在一定的外界因素作用下发生断裂失稳的过程[4]。而断裂力学是研究带缺陷或裂纹的物体或构件强度的学科[2]，因此完全可以运用断裂力学的相关理论作为手段来分析危岩的稳定性问题。只有判断危岩是否稳定才能确定是否需要对危岩进行治理以及如何治理。利用断裂力学的有关理论来分析和判断危岩的稳定性，能够为危岩稳定性分析、灾害评价及防治提供重要的理论基础。

二、基于断裂力学的危岩主控结构面应力强度因子求解方法

(一)危岩主控结构面的定义

悬崖峭壁上的危岩裂隙发育错综复杂，每个裂隙的方向、尺寸、开口宽度的情况也不同，因此对危岩的稳定性影响程度也不同。

据叶四桥对危岩体的研究认为：在不利于岩体稳定的结构面中对岩体稳定性起主要作用的结构面称为主控结构面。该结构面相对于其他结构面更容易发生裂隙扩张，引起岩体失稳[4]。

据应力强度因子理论:裂纹有三种基本类型:张开型或拉伸型(Ⅰ型)，平面剪切型滑移型(Ⅱ型)，反平面剪切型(Ⅲ型)[9]，除了这三种类型外，两种或多种裂纹的组合叫做复合型裂纹问题。危岩体受到各种荷载组合的作用，其主控结构面主要是复合型裂纹。

叶四桥，唐红梅等人认为危岩体主要由脆性岩石组成[4，9]，危岩裂隙的扩展断裂可利用线弹性断裂力学的相关理论分析处理[9]。当前，己有计算各种裂纹应力强度因子的手册。据研究文献[5-6]，各类复合裂纹断裂准则可以某种形式表示，即

Kl=KIC

KIC—岩石的断裂韧度。

(二)主控结构面应力强度因子的计算方法

据叶四桥对危岩的研究认为:作为单一的危岩体，它通常是作为一个平面应变问题来处理以简化其计算模型[4]。对于一个具体的危岩，发展到一定的时间段，它的主控结构面管通长度、结构尺寸等几何参数是可以通过现场实测的。作用在危岩上的荷载也是可以通过现场确定的。无论是何种类型的危岩，只要它的荷载以及物理模型可以确定，就可以对它进行断裂力学理论分析。前面提到危岩主要属于脆性岩石，根据线弹性断裂力学的知识，应力强度因子具有叠加性，即

KΙ=Kl1+Kl2+Kl3+Kl4+…

KΙΙ=KΙΙ1+KΙΙ2+KΙΙ3+KΙΙ4+…

正是由于应力强度因子具有这一特性，因此不管是什么样的危岩，只要明确了其荷载组合，对于某一块具体危岩，通过分析其在某种单独力的作用下的应力强度因子，然后再把这些力作用下的应力强度因子叠加就可以得出起主控结构面的应力强度因子。

三、危岩稳定性判断

于是，危岩体的稳定性便可通过危岩的断裂韧度和主控结构面的应力强度因子判断。结合陈洪凯对危岩的研究，定义危岩稳定性系数[7]为

式中，Kl需要通过应力强度因子手册结合危岩的具体工况求解；通过对危岩岩块进行试验测试可测得断裂韧度KIC。

四、工程实例

重庆市万州区是典型的危岩发育地带。现以万州太白岩某危岩(如图1)为例进行稳定性断裂力学方法分析。

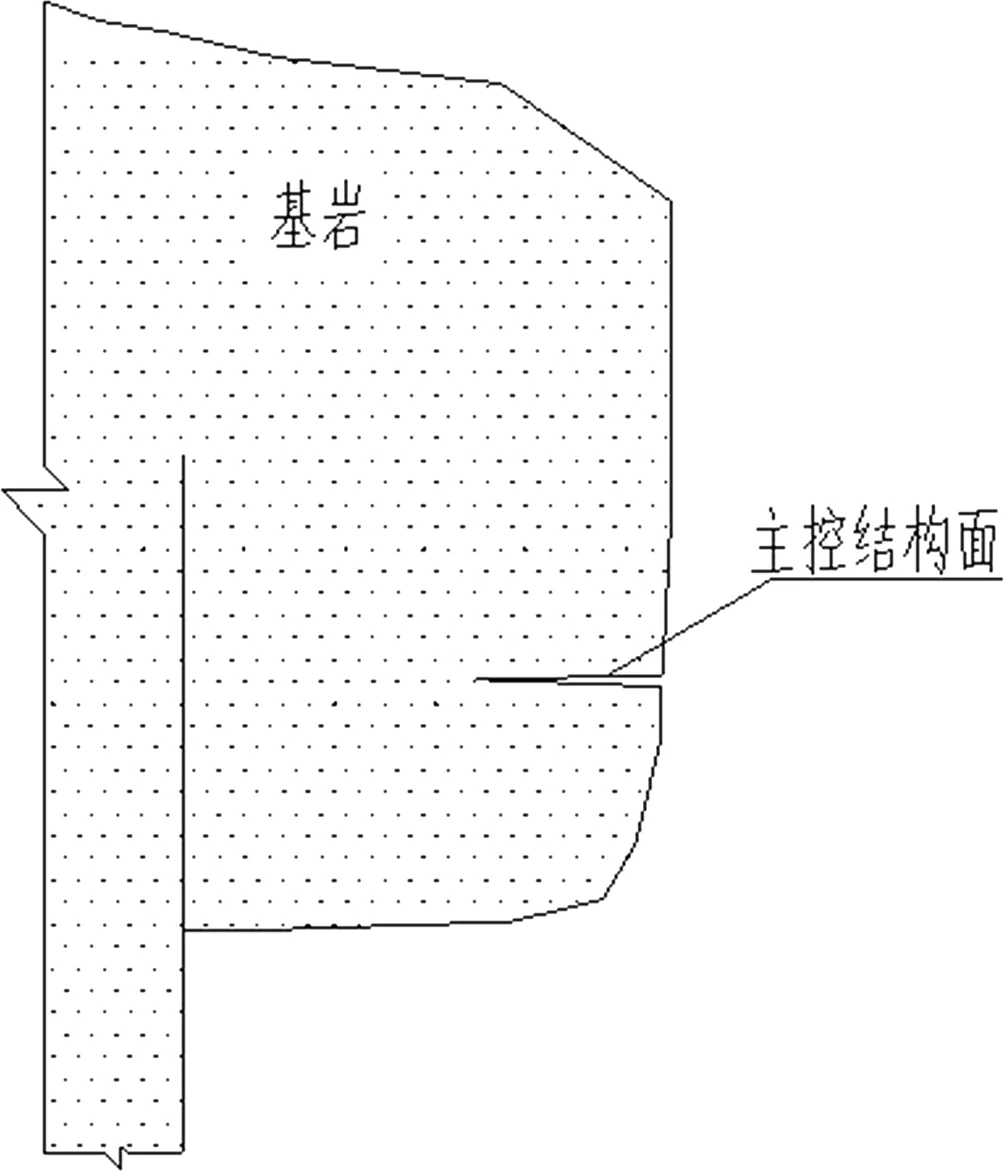
图1 万州太白岩某危岩

将危岩尺寸作一定的优化，其计算模型及尺寸见图2。

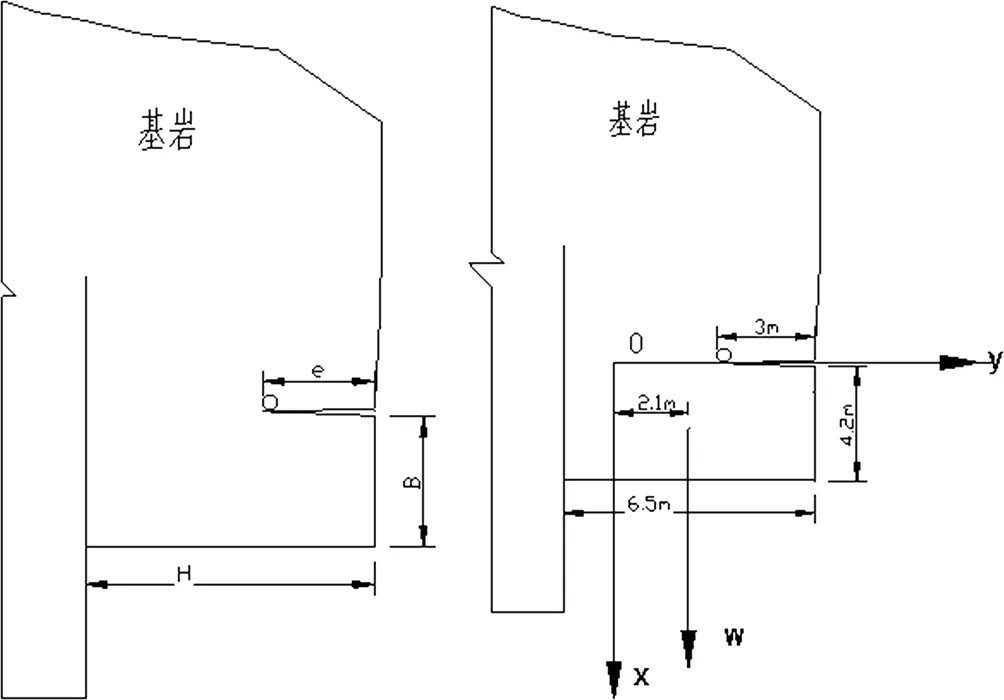
图2 危岩各部分尺寸

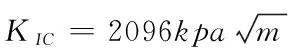
该危岩的受力如图2所示，根据现场监测其裂隙为张开型。岩块主要受重力荷载，为简化模型，取单位宽度岩块，受力分析如图2。

根据图2所示，该坠落式危岩主控结构面大致呈水平状，竖直方向的重力荷载使其产生偏心受拉，根据前面所述危岩应力强度因子的求解方法，结合应力强度因子计算手册的相关方法，可将该危岩按照图3和图4两种类型的问题进行处理[7]。

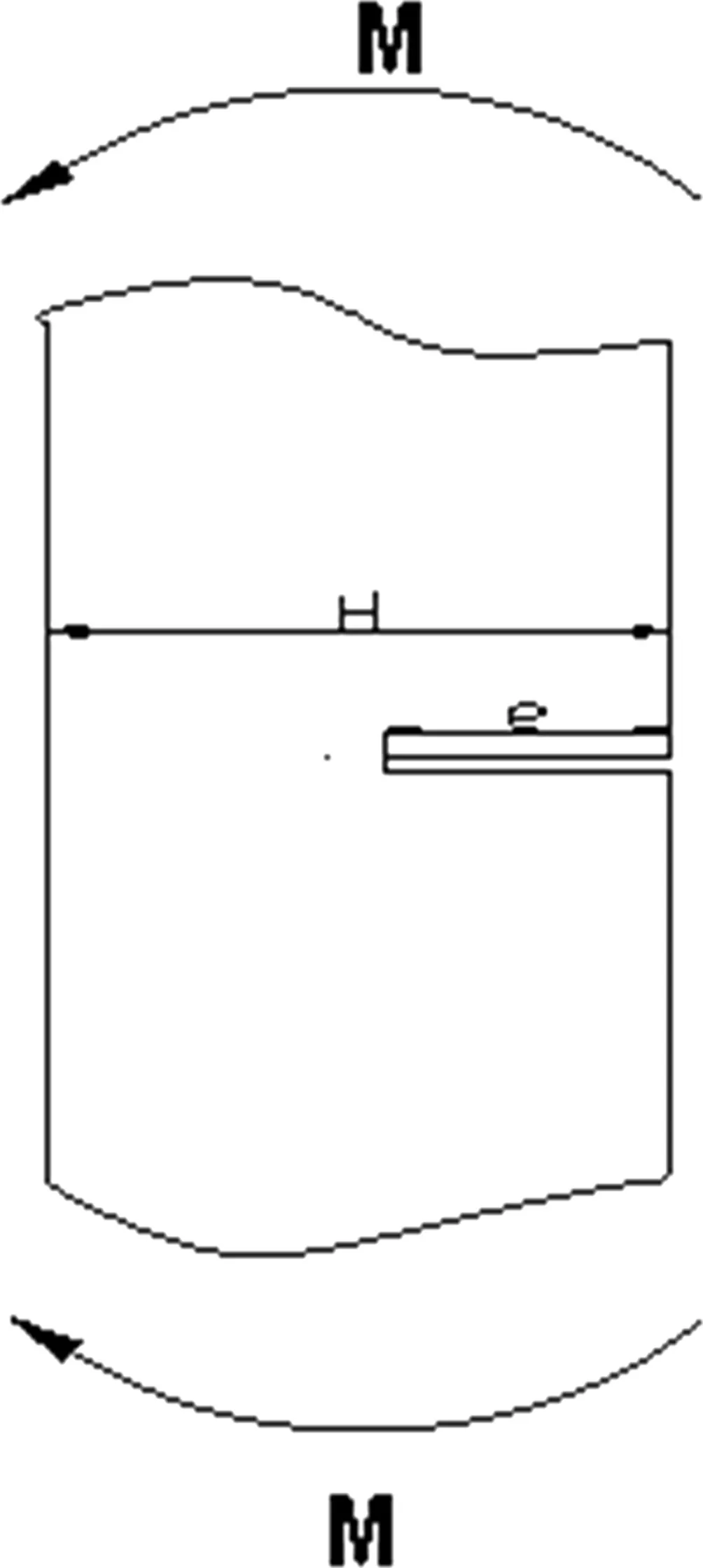
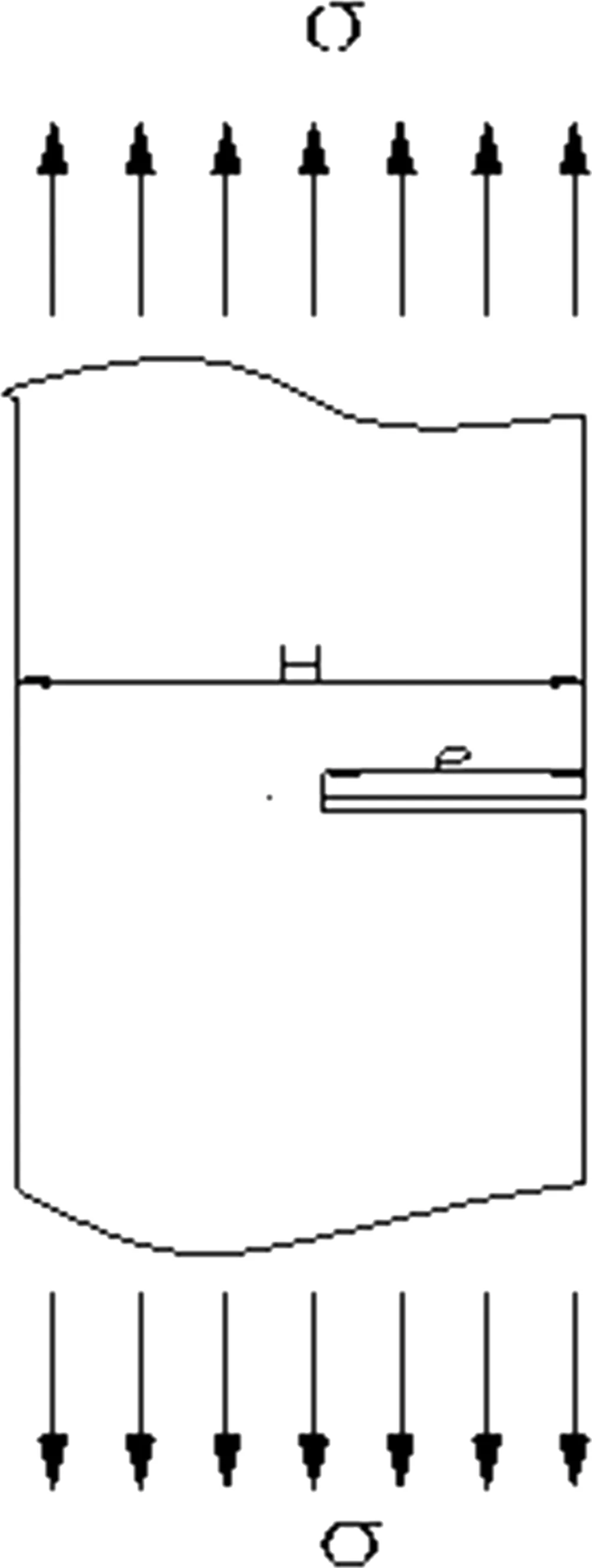
图3 单边裂纹纯弯曲[8] 图4 单边裂纹远场拉应力[8]

如图所示，e为裂隙的长度，W为单位宽度的岩块体重，H为岩块的宽度，裂纹尖端还没扩展的部分受到重力作用，形成拉力，对坐标取距为：

M=W·f=682.5×2.1=1433.25KN·m

按照应力强度因子计算手册，图3所示为有限宽板单边贯穿裂纹受纯弯曲的受力情况[8]，可按以下式子计算其应力强度因子

F(x)=1.122-1.40(x)+7.33(x)2-13.08(x)3+14.0(x)4

将其应用到图2可得到危岩主控结构面受纯弯曲的应力强度因子：

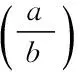
按照应力强度因子计算手册，图4为有限宽板单边贯穿裂纹受均布拉应力的情况[8]，可按下式计算其应力强度因子:

F(x)=1.12-0.231(x)+10.55(x)2-21.72(x)3+30.39(x)4

将其应用到图2可得到危岩主控结构面受拉应力的应力强度因子：

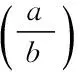
从断裂力学的角度分析，该危岩为主控结构面主要受重力作用的1型裂纹问题。按照线弹性断裂力学应力强度因子可叠加性原理可得：

该危岩稳定性计算结果为：

根据计算结果显示该危岩稳定性较好，而现场监测结果也显示该危岩稳定，说明用断裂力学分析的可行性。

五、结论

1.危岩裂隙的发育是引起失稳的主要因素。无论是何种类型的危岩，它们的稳定系数均可运用线弹性断裂力学相关理论知识求解。

2.根据应力强度因子在线弹性范围内的可叠加性，在前人的研究基础上，重点分析了太白岩某坠落式危岩的应力强度因子求解以及稳定性判断，以工程实例进行验证，证明了运用断裂力学相关理论计算危岩稳定性是切实可行的。

3.实例分析表明，运用危岩稳定性断裂分析法计算显示的危岩稳定状态客观，易于工程判别，表征了危岩破坏的本质特性，能够为危岩的稳定性分析，灾害评价以及治理提供一定的帮助。

[1]陈洪凯,胡明,唐红梅.危岩锚固机理的断裂力学分析[J].重庆建筑大学学报,2006,第5期:101-105.

[2]陈洪凯.地质灾害理论与控制[M].科学出版社,2011.1～3

[3]张晓敏,万玲,严波,张培源.断裂力学[M].清华大学出版社,2012.1～4

[4]叶四桥.危岩损伤—断裂联合机理研究[D].重庆交通学院,2004

[5]杨光里.断裂力学及应用[M].北京中国铁道出版社,1990

[6]杨卫宏微观断裂力学[M].北京人民交通出版社,1999,10

[7]陈洪凯,鲜学福,唐红梅.危岩稳定性断裂力学计算方法[J].重庆大学学报：自然科学版,2009,32(4):434-437

[8]中国航空研究院.应力强度因子手册[M].科学出版社,1993.120

[9]唐红梅,叶四桥,陈洪凯.危岩主控结构面应力强度因子求解分析[J].地下空间与工程学报,2006,第3期:393-397.