GM(1，1)模型的改进及其在火灾致死人数预测中的应用

杨坦 吴睿 王超 汪洋

(安徽新华学院土木与环境工程学院， 合肥 230088)

GM(1，1)模型的改进及其在火灾致死人数预测中的应用

杨坦 吴睿 王超 汪洋

(安徽新华学院土木与环境工程学院， 合肥 230088)

为了弥补传统GM(1,1)模型在波动数据序列预测中误差较大的缺陷，采用一阶差分方法对初始数据序列进行改进，构建了一阶差分GM(1,1)模型。分别应用传统GM(1,1)模型和一阶差分GM(1,1)模型对2009 — 2016年火灾致死人数进行预测分析。结果显示，一阶差分GM(1,1)模型的预测精度高于传统GM(1,1)模型。

GM(1,1)模型； 初始值； 一阶差分； 火灾致死人数

火灾致死人数的预测对于研究火灾事故的发生规律，分析火灾发展趋势以及制定火灾控制措施都具有重要意义。火灾事故产生的内在因素较为复杂，难以采用线性分析方法进行分析。GM(1,1)模型是灰色理论的基本模型，可用于研究非线性问题。国内外学者对GM(1,1)模型在火灾事故预测中的应用进行了分析和研究[1-3]。然而这些研究都不能很好地解决波动数据时间序列的预测问题，为进一步提高预测精度，必须对传统模型进行改进。

本次研究将通过原始数据序列的一阶差分运算，使波动数据时间序列平稳化，对数据残差进行修正。最后针对2009 — 2014年全国火灾致死人数进行预测分析，验证了模型对波动数据时间序列预测研究的有效性。

1 传统GM(1,1)模型及其改进

1.1 传统GM(1,1)模型

灰色系统理论由邓聚龙教授于1982年建立，该理论是分析少数据、少信息问题的手段，基于已知信息对未知领域进行探索，以逐步了解整个系统[4-6]。传统GM(1,1)模型的应用条件是：等时距；非负性；单调性。传统GM(1,1)模型的计算过程分以下3个步骤。

(1) 一次累加处理。设原始离散数据序列x(0)={x(0)(1),x(0)(2),…,x(0)(n)}，其中n为序列长度。按照式(1)对原始离散数据序列进行一次累加生成处理：

(1)

(2) 建立GM(1,1)模型。以新序列为基础建立GM(1，1)模型：

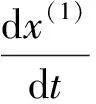
(2)

式中，a和u为待辨识参数。

设参数向量:

(3)

得到响应方程：

(4)

由于模型得出的是一阶累加量，因此建模运算后需做逆生成运算。按照式(5)将数据还原到原始数据。

(5)

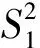
(6)

(7)

其中：

计算后验差比为：

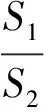
(8)

计算小误差概率 ：

(9)

指标C和P是后验差的两个重要指标。C越小就表明原始值与模拟值不相关[7]。P越大说明拟合值的分布越均匀，因此模型的精度是由C和P共同决定的。模型的精度分为4个等级(见表1)[6]。

表1 精度检验等级参照表

1.2 GM(1,1)模型的改进

传统GM(1,1)模型所选的初始值不一定合适，最初状态与待预测状态的关联度不大。按以下步骤对初始值进行改进[8-9]。

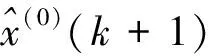
=(1-ea)[x(0)(1)+σ-ua]e-ak

(10)

整理后得：

(11)

(2) 确定修正值σ的值：

解得：

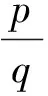
(12)

其中

2 模型实例计算结果对比

以2009 — 2016年全国火灾死亡人数原始数据(见表2)为基准数列，建立火灾致死人数的GM(1,1)模型和改进的GM(1,1)模型，分别计算各年份的火灾致死人数预测值，并与实际值进行误差比较。

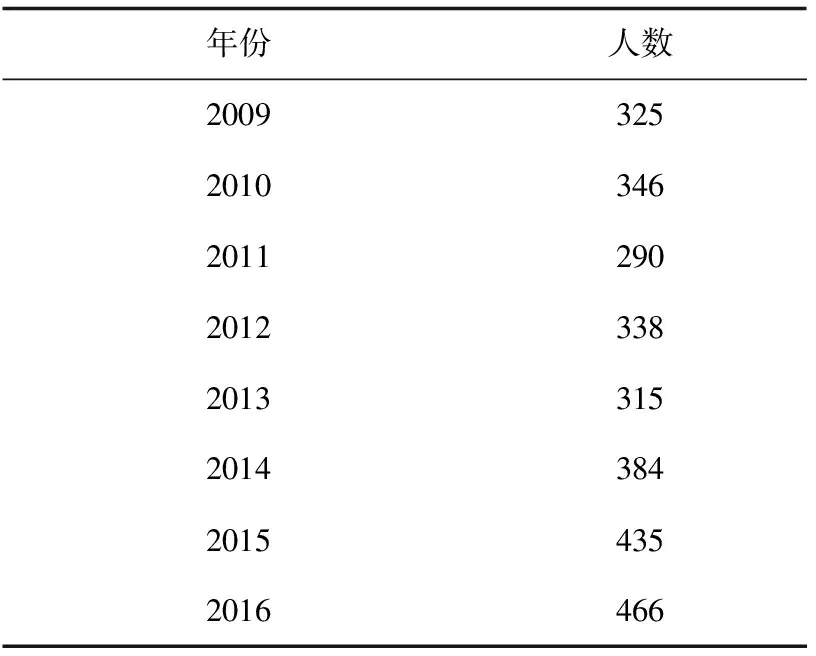
表2 2009 — 2016年火灾致死人数原始数据

2.1 传统GM(1,1)模型计算结果

利用公式(1)— (9)对2009 — 2016年火灾致死人数进行分析，计算得到：

a=-0.071 595，u=-259.421 711

故其时间响应函数为：

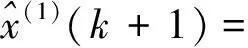
3 623.460 489

2.2 改进的GM(1,1)模型计算结果

利用公式(10)和(11)对2009 — 2016年火灾致死人数进行分析，计算得到：

P=3 856.650 84

q=0.962 258 958

σ=59.452 389 47

故初始值调整后的预测公式为：

2.3 两种模型计算结果比较

根据公式(5)和公式(12)对表2数据进行计算，分别得到按传统模型计算和按改进模型计算的火灾致死人数预测值(见表3、表4)。

将两种模型的计算结果与实际值进行比较，绘制火灾致死人数预测图(见图1)。

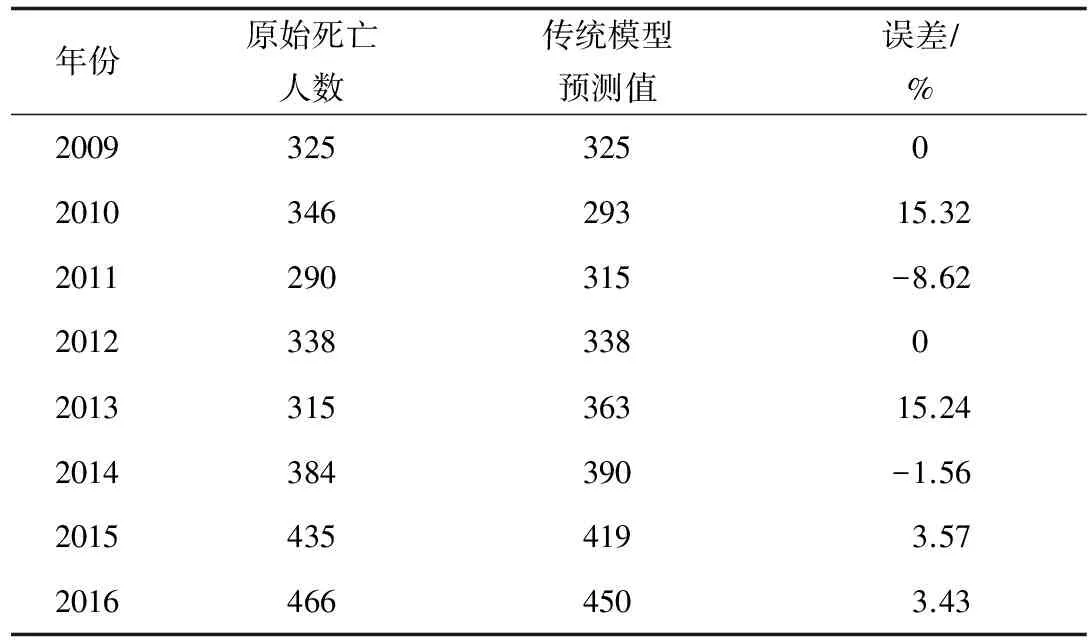
表3 火灾致死人数预测结果(按传统模型计算)

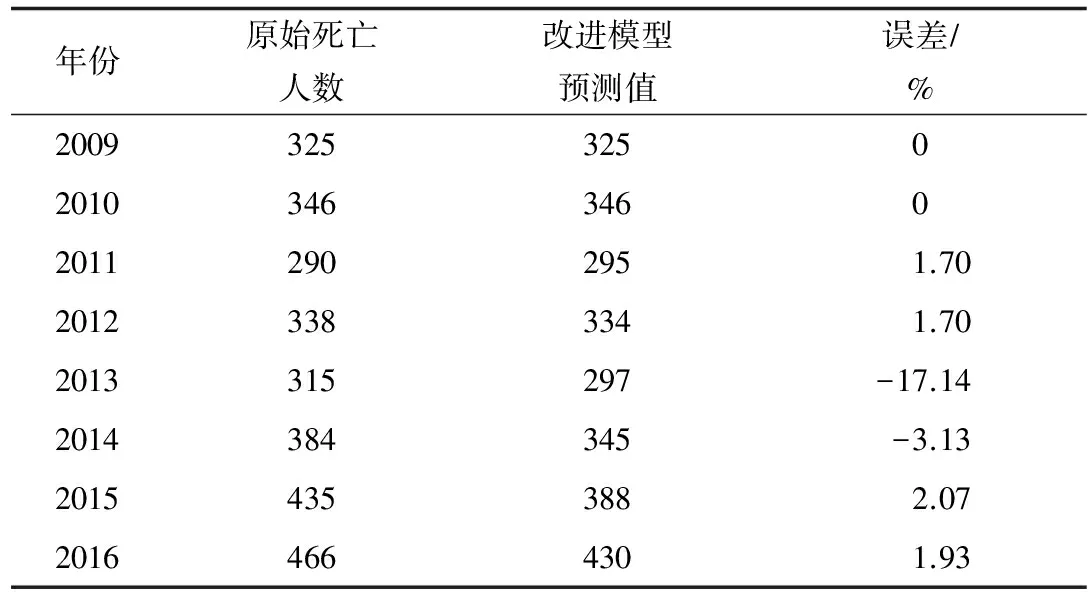
表4 火灾致死人数预测结果(按改进模型计算)

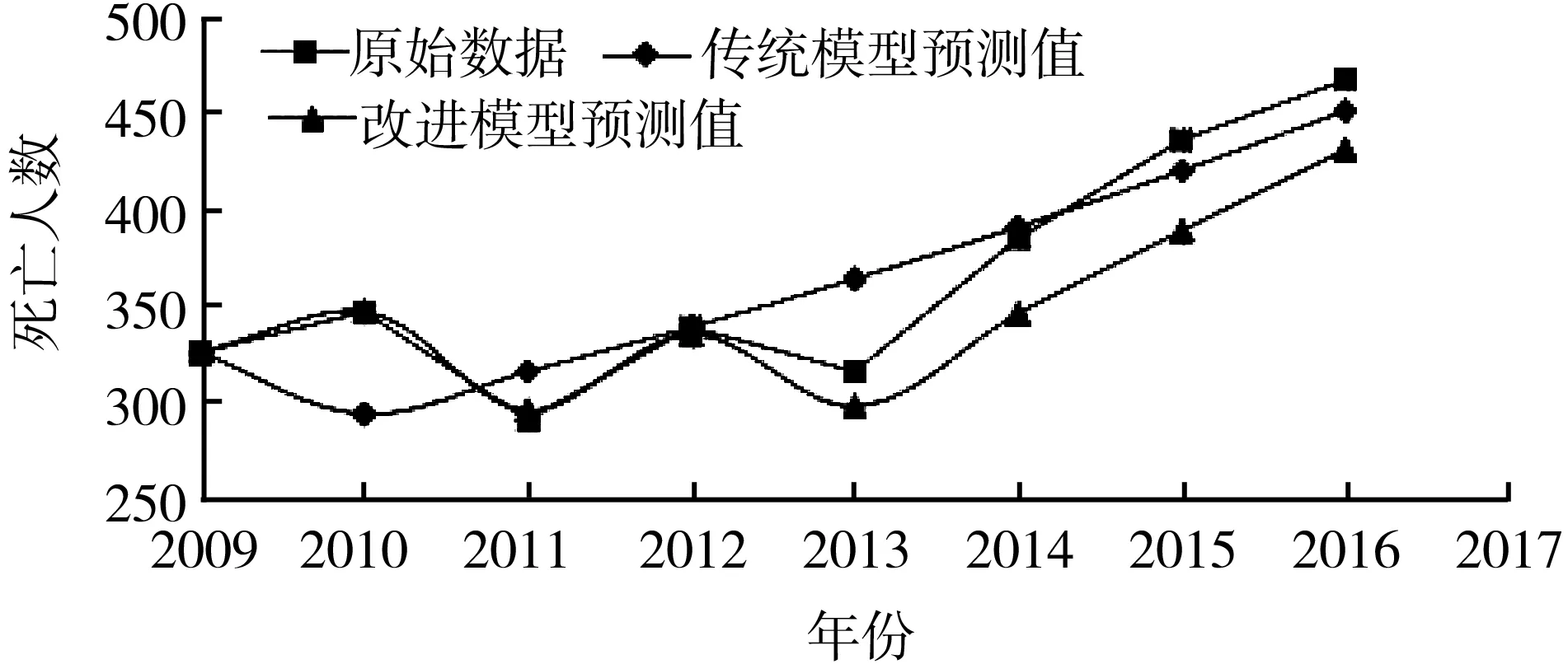
图1 火灾致死人数预测图

传统模型计算的残差序列方差分别是，S1=3 277.734 375，S2=785.187 5，后验差比C=0.239 551 9。虽然计算精度达到好的程度，但是传统GM(1,1)模型建模结果显示，误差最高达到15%以上，最小接近0，平均相对误差为6.84%，数据波动非常大。经过一阶差分处理后，将最高误差从15.00%降到10.00%左右，各个数据点的误差也有所下降，平均误差从6.84%下降到4.70%。与传统GM(1,1)模型建模结果相比，改进模型的平均精度提高了30.88%，提高效果显著。

3 结 语

传统GM(1,1)模型的初始值对预测结果影响较大。采用一阶差分方法对初始值进行修正，能够解决波动数据对预测结果的干扰，提高了预测结果的精度。改进模型的预测结果显示，各个数据点的误差均有所下降，平均误差从6.84%下降到4.70%。与传统GM(1,1)模型建模结果相比，改进模型的平均精度提高了30.88%，效果显著。研究表明，一阶差分建模的方法有效可行。

[1] 谢正文.火灾预测的改进GM(1,1)模型[J].中国计量学院学报，2007，18(3)：241-243．

[2] 王换鹏.GM(1,1)模型的优化研究[D].秦皇岛：燕山大学，2012：5-11．

[3] 吴天魁，王波.火灾损失预测的改进GM(1,1)模型[J].数学理论与应用，2014，34(1)：58-70.

[4] 邓聚龙.灰色系统理论教程[M].武汉：华中理工大学出版社,1992：20-30.

[5] 邓聚龙，刘思峰.GM(1,1)模型的适用范围[J].系统工程理论与实践，2000(5)：121-124．

[6] 刘思峰，曾波，刘解放，等.GM(1,1)模型的几种基本形式及其适用范围研究[J].系统工程与电子技术，2014，36(3)：501-508．

[7] 温丽华.灰色系统理论及其应用[D].哈尔滨：哈尔滨工程大学，2003:8-11．

[8] 张大海，江世芳，史开泉.灰色预测公式的理论缺陷及改进[J].系统工程理论及实践，2002(8)：140-142．

[9] 赵晓芬.灰色系统理论概述[J].吉林省教育学院学报，2011，27(3):152-154．

ImprovementofGM(1,1)ModelandItsResearchonthePredictionofFireMortality

YANGTanWURuiWANGChaoWANGYang

(Civil and Environmental Engineering College, Anhui Xinhua University, Hefei 230088, China)

In order to solve the problem that the traditional GM (1,1) model has large error in the prediction of wave data sequence, the first-order difference GM (1,1) model is constructed based on the first-order difference method. Both of the two models are applied to predict the number of fire deaths from 2009 to 2016 respectively. The results show that the prediction accuracy of the first - order difference GM (1,1) model is higher than that of the traditional GM (1,1) model.

GM (1,1) model; initial value; first order difference; number of fire deaths

2017-06-20

国家自然科学基金项目“城市变化环境下水资源系统脆弱性机理及其对人类活动的响应研究”(51309004)；安徽新华学院校级科研团队建设项目 “安全工程科研团队” ;安徽新华学院科研团队研究项目“灰色 — 尖点突变模型在建筑火灾发展趋势预测中的应用”(2016TD012)；安徽省大学生创新创业训练计划项目“基于改进型GM(1,1)模型的火灾事故预测研究” (AH201512216014)

杨坦(1987 — )，男， 安徽合肥人，讲师，研究方向为系统安全预测。

X932

A

1673-1980(2017)06-0083-03