边坡坡角对地基极限承载力的衰减效应

陈 园

（新疆水利水电勘测设计研究院，乌鲁木齐830000）

边坡坡角对地基极限承载力的衰减效应

陈 园

（新疆水利水电勘测设计研究院，乌鲁木齐830000）

为研究边坡角大小对地基承载力的影响，采用有限元载荷试验进行数值模拟计算，建立了简化的地基及边坡—地基模型，计算出地基的极限承载力大小，并分析了地基的极限承载力随着边坡坡角的变化规律。结果表明：载荷试验下，模型的等效塑形区不断上移，当模型破坏时，等效塑形区完全位于地基破坏区域；在相同的基础载荷情况下，边坡—地基模型随着坡角的增加，模型整体位移不断增加，且增加幅度较缓；当载荷达到一定时，位移出现突变，并且增加幅度变大；边坡的形成将对地基极限承载力有衰减效应，并且地基极限承载力的衰减效应随着坡角的增加总体呈非线性变大趋势，但其衰减效应幅度随着坡角的增加逐渐变缓。

地基；边坡坡角；等效塑形区；极限承载力；衰减效应

边坡坡顶上修建各种建筑物，现在已经广泛应用于土木工程、岩土工程及水利工程中。这些工程能够较好的监控及预测一些不安全因素，使工程更加安全［1-4］。

考虑地基承载力时，主要考虑地基的强度及变形两方面，计算地基承载力特征值时是为了控制实际基础沉降的深度。众多学者对其研究主要分为两个方面：一方面通过传统极限平衡理论进行等效的水平地基计算，该方法简单方便，但是不能充分体现出地基为非水平方向，即无法展示边坡对地基的承载力影响；另一方面综合边坡的基本因素 （边坡角度、基础位置等等），通过不同的假设及理论，致使结果出现较大差异，降低其应用价值。但将边坡稳定性及地基极限承载力结合分析相对较少。

本文通过前人的研究基础，采用数值计算的手段，进而分析了坡角变化下“边坡—地基”极限承载力Pu的衰减效益。

1 地基极限承载力分析

极限承载力即为结构在破坏临界点所能承受的最大承载力。最早学者通过塑性平衡理论推导出考虑材料参数的水平地基极限承载力公式，随后，不断有学者在此基础上进行完善与改进，其中Terzaghi公式［5-6］应用最为广泛，可用式（1）表示（基础埋深不为0时）：

当基础埋深为0时，可将式（1）简化为：

式中 Nγ，Nc，Nq分别为水平地基极限承载力系数。

随着水平地基极限承载力研究的不断深入，在此基础上不断完善地基的形状、深度、荷载作用的方向及“边坡—地基”形势等对极限承载力的影响，主要采用极限平衡理论对其受力变形特性和破坏机理方面进行严谨地分析和计算。

以上通过基于Prandtl解的各种经验修正及改进解析公式，然而实际工程中主要是通过有限元数值模拟，将现场工程的复杂地质条件简单化。有限元数值模拟的主要方法是通过增量加载法，能够较为真实地模拟出地基载荷情况。因此，本文通过大型岩土软件，并对模型地基进行等量增加载荷计算，最后获得计算结果，进一步求解地基极限承载力分析。

2 数值模拟

2.1 模型建立

根据某工程“边坡—地基”为背景，对该类工程进行简化计算，建立地基及边坡—地基模型，同时上部为均布荷载（Q），荷载作用宽度（B），容重γ，黏聚力c，内摩擦角φ，其中弹性模量E取120MPa，泊松比υ取0.25。所有模型坡高为20m，以及边坡L1长度为40m，计算中土体参数采用摩尔库伦模型参数，如图1。

图1 简化模型

在该土质边坡尺寸和土体参数条件下，改变边坡坡角β，建立不同的计算模型，其中β取0°（地基），10°，20°，30°，40°，50°，60°（边坡—地基）， 共7个模型，其中β取0°时，表示的是地基模型为L×H1（200m×20m）的矩形地基。

2.2 边界及计算方法

通过以上7个模型尺寸，建立网格为1m的有限元模型，采用摩尔库伦准则分析，约束模型两侧的水平位移及底部的水平和竖向位移，然后在均布荷载作用区域施加相应的荷载作用，最后采用等量增加载荷试验进行 （模型通过增量加载法，设置总荷载为5000kPa，分1000步进行加载，每步5kPa）模拟，当模型计算过程中无法达到收敛状态，即可以结束该模型的计算。

3 分析及讨论

3.1 地基及边坡—地基稳定性分析

通过观察7种计算模型的分析结果，在不同坡角β情况下边坡—地基随荷载Q增大的变形破坏模式基本类似，鉴于篇幅，仅给出β=30°（边坡—地基）的结果图，如图2。

图2 坡顶地基初始状态下的塑性云图（β=30°）

从图2可观察到，基础荷载对边坡—地基的破坏模式影响很大。对于Q=0时，即边坡上部不设基础，此时边坡等效塑性区主要集中在边坡中部。在基础施加荷载后，当Q较小时，其等效塑性区所在区域基本保持不变，随着Q的逐渐增大，坡体的塑性逐渐上移，最后基础下部逐渐发生了局部破坏。最后当Q达到一定时，坡体的塑性完全集中在坡顶外侧，坡顶外侧土体已经完全隆起，边坡—地基完全破坏。

3.2 地基及边坡—地基的极限承载力计算

通过以上7种模型结果分析，在不同的坡角β情况下，以模型计算不能达到收敛状态为结束界限，进一步对模型的监测点进行位移分析，当位移载荷曲线达到突变时，即可认定为模型地基的极限承载力。

图3～图9为7种不同坡角模型的载荷中心点位移与载荷关系曲线。可以得出在相同的基础载荷情况下，边坡—地基模型随着坡角的增加，模型整体位移不断增加，且增加幅度较缓；当载荷达到一定时，位移出现突变，并且增加幅度变大。总体而言，随着基础载荷的逐渐增大，其位移越来越大。

图3 坡角0°（地基）荷载中心点位移与载荷关系

图4 坡角10°（边坡—地基）荷载中心点位移与载荷关系

图5 坡角20°（边坡—地基）荷载中心点位移与载荷关系

图6 坡角30°（边坡—地基）荷载中心点位移与载荷关系

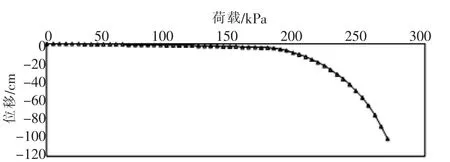
图7 坡角40°（边坡—地基）荷载中心点位移与载荷关系

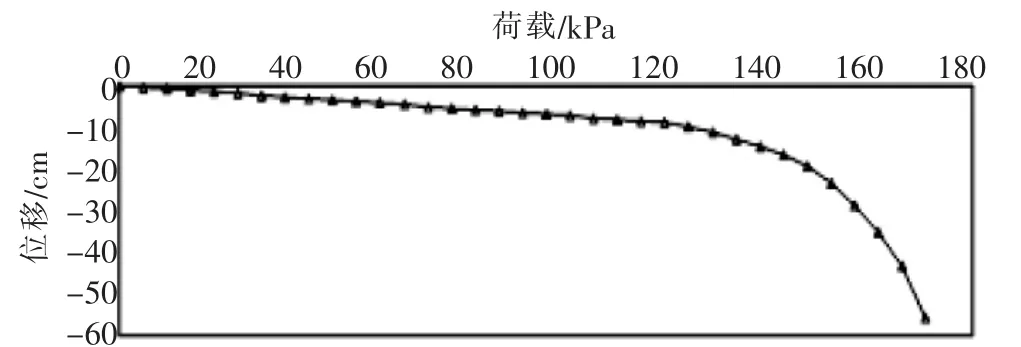
图8 坡角50°（边坡—地基）荷载中心点位移与载荷关系

图9 坡角60°（边坡—地基）荷载中心点位移与载荷关系

根据载荷试验模拟出地基及边坡地基位移与荷载之间的关系曲线，并通过计算可以得出不同坡角大小情况下的模型极限承载力大小 （认定当模型监测点位移出现突变前的荷载大小为极限承载力大小）。计算得出模型坡角从0°（地基）到60°（边坡—地基） 的极限承载力大小分别为1150，875，670，350，175，115，100kPa。

3.3 地基及边坡—地基极限承载力分析

通过分析以上7种模型结果，以及拟合出的不同坡角情况下的位移与载荷关系曲线，得到地基及不同坡角下的边坡—地基的极限承载力大小。图9为坡角大小与极限承载力关系曲线。

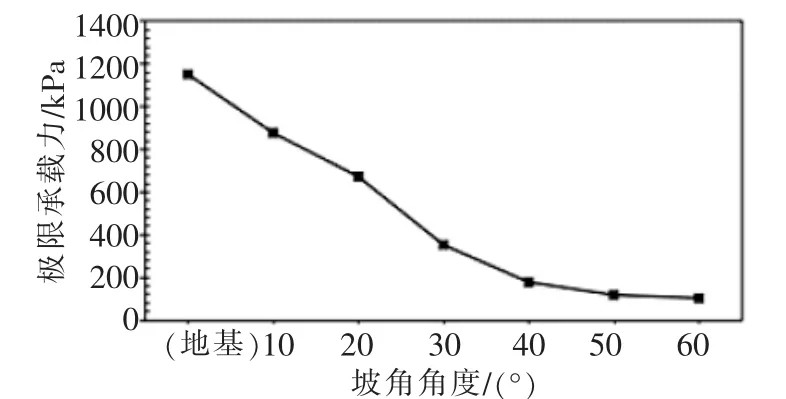
图9 坡角大小与极限承载力关系

结果表明，地基承载力随着坡角β的增加总体呈减小趋势，即边坡将对地基极限承载力有衰减效应。

图10为边坡坡角对地基极限承载力的衰减效应曲线。

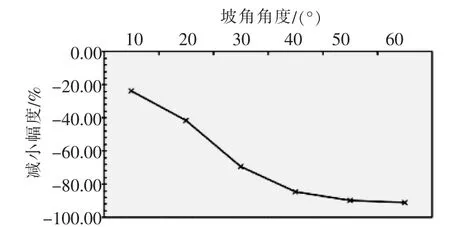
图10 边坡坡角对地基极限承载力的衰减效应曲线

从图10中可以看出，边坡形成后，地基的极限承载力衰减效应随着坡角的增加总体呈非线性增加趋势，即坡角越大，边坡—地基的极限承载力相对于地基的极限承载力衰减效应越大，但是其衰减效应幅度随着坡角的增加逐渐变缓。

4 结语

（1）有限元载荷试验结果等效塑形云图显示，地基及边坡—地基在载荷不断增加下，其等效塑形区从边坡中部不断向上移动，最后位于地基载荷处；当模型完全破坏时，地基—边坡顶部外侧完全隆起，即有限元载荷试验能够通过对模型的位移对地基及边坡—地基极限承载力进行计算。

（2）在相同的基础载荷情况下，边坡—地基模型随着坡角的增加，模型整体位移不断增加，且增加幅度较缓；当载荷达到一定时，位移出现突变，并且增加幅度变大。

（3）边坡的形成将对地基极限承载力有衰减效应，并且地基的极限承载力衰减效应随着坡角的增加总体呈非线性变大趋势，即坡角越大，边坡—地基的极限承载力相对于地基的极限承载力衰减效应越大，但是其衰减效应幅度随着坡角的增加逐渐变缓。

［1］郑颖人，陈祖煜，王恭先，等.边坡与滑坡工程治理［M］.北京：人民交通出版社，2007.

［2］钱家欢，殷宗泽.土工原理与计算（第二版）［M］.北京：中国水利水电出版社，1996.

［3］Zhu H H， Wang Z Y， Shi B， et al.Feasibility study of strain based stability evaluation of locally loaded slopes：Insights from physical and numerical modeling ［J］.Engineering Geology， 2016， 208：39-50.

［4］Ni P， Wang S， Zhang S， et al.Response of heterogeneous slopes to increased surcharge load ［J］.Computers&Geotechnics，2016，78：99-109.

［5］赵杰，邵龙潭.土体结构极限承载力的有限元分析［J］.岩石力学与工程学报， 2007， 26（S1）：3183-3189.

［6］GBJ7—89，建筑地基基础设计规范［S］.

Attenuation effect of slope angle on ultimate bearing capacity of foundation

CHEN Yuan
（Xinjiang Institute of water resources and Hydropower Survey and design， Urumqi 830000，China）

In order to study the influence of slope angle on the bearing capacity of foundation， the finite element load test is used to simulate the foundation.The simplified foundation and slope-foundation model are established to calculate the ultimate bearing capacity of the foundation and analyzed the limit of the foundation bearing capacity changes along the slope angle.The results show that under the load test，the equivalent shaping area of the model is continuously moved up.When the model is destroyed，the equivalent shaping area is completely located in the ground failure area.Under the same base load， as the angle is increases， the overall displacement of the model increases， and the increase is slower.When the load reaches a certain time，the displacement becomes abrupt and the increase is larger.The formation of the slope will have the attenuation effect on the ultimate bearing capacity of the foundation.The attenuation effect of force is increases nonlinearly with the increase of slope angle，but its attenuation effect gradually decreases with the increase of slope angle.

foundation； slope angle； effective plastic area； ultimate bearing capacity； attenuation effect

P642；TU459 文献标识码：A 文章编号：1672-9900（2017）06-0086-04

2017-08-22

陈 园（1986-），男（汉族），新疆乌鲁木齐人，工程师，主要从事施工组织、水利工程施工等方向研究，（Tel）15800541557。

尹健婷）