FRP加固局部损伤偏心受压钢压杆的弹塑性失稳分析
李 斌, 李传习, 罗 华, 王玮玮
(1.湖南理工学院 土木建筑工程学院,湖南 岳阳 414000; 2.长沙理工大学 土木与建筑学院,湖南 长沙 410076)
FRP加固局部损伤偏心受压钢压杆的弹塑性失稳分析
李 斌1, 李传习2, 罗 华1, 王玮玮1
(1.湖南理工学院 土木建筑工程学院,湖南 岳阳 414000; 2.长沙理工大学 土木与建筑学院,湖南 长沙 410076)
文章考虑初弯曲和初偏心2种几何缺陷的影响,基于Ježek法推导纤维增强复合材料(fiber reinforced plastic,FRP)加固局部损伤偏心受压钢压杆绕强轴弹塑性失稳时极限荷载的计算公式。利用有限元软件验证了该解析公式的正确性与可靠性,并对影响局部损伤钢压杆弹塑性极限荷载的有关参数,例如FRP加固长度、厚度、宽度以及初弯曲和初偏心等初始几何缺陷进行分析,得到了FRP合理加固建议以及各参数的影响规律。结果表明,FRP在加固、恢复甚至提高含初始缺陷的局部损伤钢压杆弹塑性稳定性方面具有良好的可加固性和优越性。
纤维增强复合材料(FRP);局部损伤;偏心受压钢压杆;弹塑性稳定
近年来,纤维增强复合材料(fiber reinforced plastic,FRP)因其轻质高强、施工方便快捷、耐腐蚀性好等优点,被广泛应用于钢结构加固和修复工程中[1]。
国内外应用FRP增强和加固钢结构的研究和工程应用主要集中在受弯性能[2-4]、受拉性能[5-6]、黏结性能[7-8]和疲劳性能[9]等方面,针对FRP加固钢结构的受压性能和屈曲性能的研究还很不充分[10],少量的研究成果也只局限于弹性屈曲分析[10-12]。由于FRP抗拉强度高于钢材,荷载作用下,钢压杆部分截面进入塑性状态时,FRP依然处于弹性状态,可以有效抑制钢压杆受拉区的变形与塑性发展,从而提高构件承载力。而FRP主要提高的是钢结构塑性承载力[13],因此,研究FRP加固钢结构的弹塑性失稳状态十分必要。
在实际工程中,一方面由于设计、制造、运输和安装等原因钢压杆不可避免地会产生微小的初弯曲和初偏心; 另一方面由于锈蚀、疲劳、腐蚀等因素,大量钢压杆往往存在不同程度的局部损伤,急需通过加固预防或延缓腐蚀、疲劳和失稳破坏。文献[13-15]研究了初弯曲影响下,全梁长范围,上、下两侧粘贴FRP前后,矩形、H形、方形等截面形式压弯构件绕强轴失稳时的弹塑性极限荷载,并证明了Ježek法求解压弯钢构件弹塑性失稳问题的可靠性以及FRP提高压弯构件弹塑性极限承载力的有效性。文献[13-15]的研究成果,一方面,主要针对FRP增强无损压弯构件的弹塑性失稳性能,难以直接应用于局部损伤构件; 另一方面,钢压杆的弹塑性极限一般取决于内力最大的截面,全梁长范围粘贴FRP的加固方式也不经济,而且对受压侧粘贴FRP进行加固难以发挥FRP的材料性能,因此,这种FRP加固方式与实际加固工程既要安全可靠又要经济的现实不相符。
本文充分考虑钢压杆一般存在初弯曲和初偏心等初始几何缺陷的工程实际,采用FRP加固钢压杆损伤区域的受拉侧(损伤侧),基于Ježek法推导FRP加固局部损伤偏心受压钢压杆弹塑性失稳时的极限荷载。
1 基本假定
两端铰支、长为l的局部损伤矩形截面钢压杆,损伤区域位于最危险的中部受拉侧。沿构件的轴线方向粘贴FRP对损伤区域进行加固,加固示意图以及构件尺寸如图1所示。图1中,B为截面宽度;H、h分别为无损区域高度、损伤区域高度;ld为损伤区域长度;lf、b、t分别为FRP加固长度、宽度及厚度。

图1 FRP加固局部损伤钢压杆示意图
假设钢压杆初始变形曲线为y0=v0sin(πx/l),偏心荷载F(偏心距为e)作用下的变形曲线为y1=v1sin(πx/l),构件总体变形为两者之和,如图2所示。其中,v0、v1分别为构件中点截面的初始变形及荷载作用下的变形。杆件为理想弹塑性材料,FRP为线弹性材料。FRP与构件在弹塑性发展全过程结合面上无相对滑移,且不考虑局部损伤可能引起的应力集中。

图2 钢压杆偏心受压变形示意图
2 钢压杆中点弹塑性失稳时的极限荷载
2.1 受压侧出现塑性区
图2所示的钢压杆经FRP加固后,可能在构件中点发生弹塑性失稳,应变沿截面高度的分布满足平截面假定,应力、应变分布情况如图3所示。

图3 受压区单侧屈服时的应变和应力
图3中,d为截面弹性核高度(阴影部分表示塑性区);φ为失稳截面的曲率;εt、εy分别为构件下表面(或FRP)应变和屈服应变;σy、σt、σf分别为构件屈服强度、下表面应力及FRP的应力,且σy=Eεy,σt=Eεt,σf=Efεt;E、Ef分别为构件和FRP的弹性模量。
由静力平衡条件可得失稳截面轴力FN和弯矩M分别为:
(1)
F(e+v0+v1)
(2)
其中,λ为常数,λ=Ef/E。
截面的曲率为:
由(3)式可解得:
σt=k(x)v1d-σy
(4)
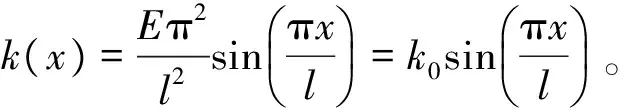
将(4)式分别代入(1)式、(2)式,且x=l/2,可得:
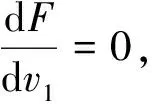
联立(5)~(7)式可以求得钢压杆中点截面发生弹塑性失稳时的极限荷载。
2.2 受压、受拉侧出现塑性区
当x=l/2截面受压、受拉侧均出现塑性区时,应变和应力示意图如图4所示。图4中,c为截面受拉侧塑性区高度。
由静力平衡条件得:
F=Bhσy-Bσy(d+2c)-Efεtbt
(8)
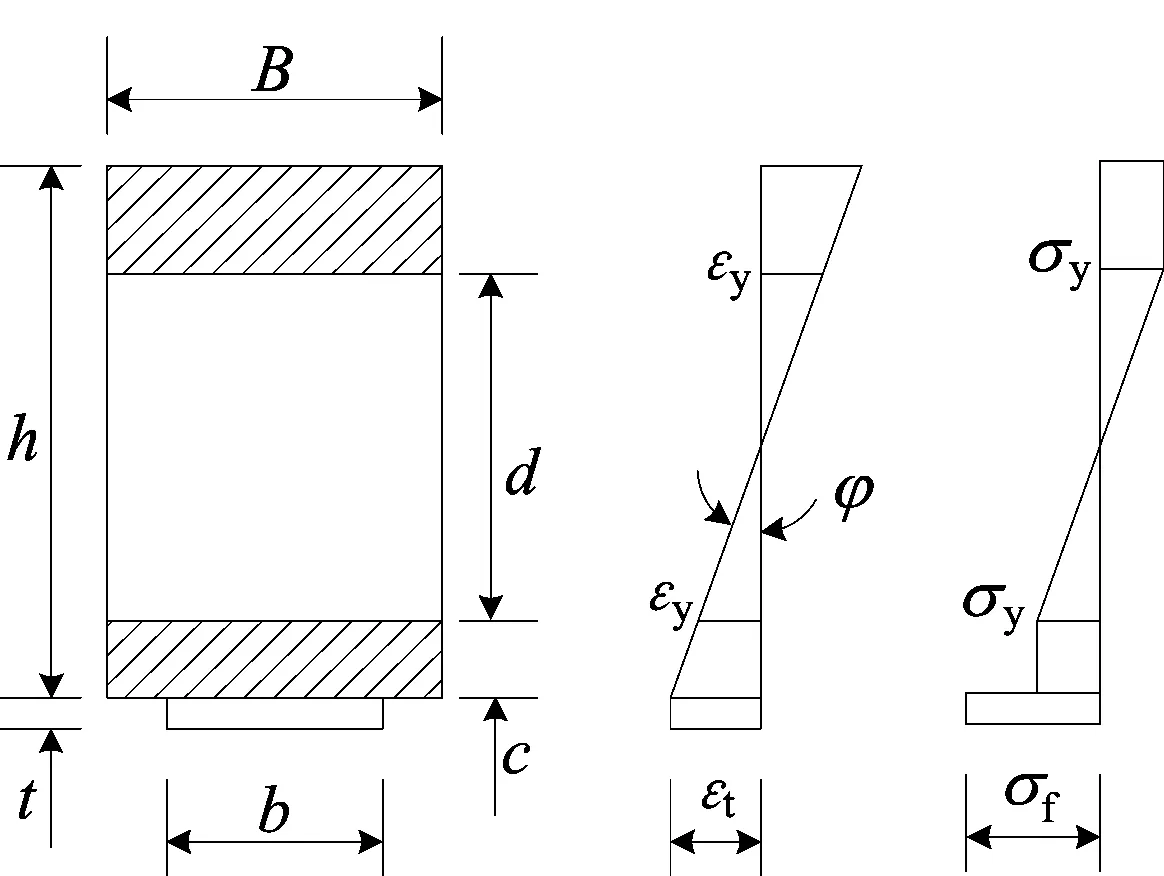
图4 双侧屈服时的应变和应力
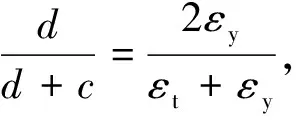
将(10)式、(11)式代入(8)式解得:
其中
进一步将(10)~(12)式代入(9)式可得:
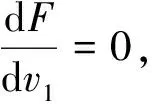
联立(10)式、(13)~(15)式可以求得钢压杆中点截面发生弹塑性失稳时的极限荷载。
3 钢压杆弹塑性失稳时的极限荷载
3.1 经FRP加固的钢压杆
通过上述分析推导可知,经FRP加固后的偏心钢压杆可能在构件中点发生弹塑性失稳,且可能存在2种应力、应变分布状态(图3或图4)。通过计算图3状态下极限荷载以及构件受拉侧边缘应力σt,根据边缘应力是否达到屈服应力,可以判断该截面受压、受拉侧是否同时出现塑性区,从而确定构件中点截面发生弹塑性失稳时的极限荷载Fu1。
经FRP加固的局部损伤钢压杆还可能在x=l1截面(见图1)先于构件中点截面发生弹塑性失稳。该截面弹塑性失稳时的应变和应力分布示意图与图3或图4相同,可以利用现有公式,进行适当的参数替换求解得到极限荷载。此时,截面弯矩为:
M=F[e+v0sin(πl1/l)+v1sin(πl1/l)],
与FRP有关的参数b=0、t=0,k0用k(l1)替换,由此计算得到x=l1截面处的极限荷载,记为Fu2,则钢压杆的极限荷载Fu取Fu1与Fu2的较小值。若l1 无损构件经FRP加强的弹塑性极限荷载求解方法与局部损伤构件的求解方法相同,此时,参数h全部由H替换。 未经FRP加固的构件必将在构件中点截面发生弹塑性失稳。令(1)~(15)式中参数b=0、t=0,再求解极限荷载Fu。同理,如果是无损构件,还应将公式中的参数h全部用H替换。 为了考察本文理论公式的精确程度,采用本文方法计算图1所示局部损伤偏心受压矩形截面钢压杆的弹塑性极限荷载,并与有限元计算结果进行了对比,见表1所列。 算例1 已知钢压杆长8 m,B=0.1 m,H=0.2 m。初偏心e=l/1 000,最大初始挠度v0=l/1 000。损伤区位于最危险的构件中部受拉侧,ld=1 m,h=0.198 m。钢材屈服极限σy=235 MPa,E=206 GPa,为理想的弹塑性材料。FRP的弹性模量Ef=235 GPa,单层厚度tf=0.835 mm。FRP纵向粘贴于钢柱损伤区域,加固厚度t=0.835 mm,lf=1.1 m,b=0.1 m。 表1 算例1计算结果对比 本文方法与有限元计算结果表明,该钢压杆中点截面首先发生弹塑性失稳,受拉侧边缘应力σt小于屈服应力,构件处于仅受压侧出现塑性区的失稳状态。由表1可知,2种方法计算结果吻合情况较好,证明了本文计算理论与公式的正确性和精确性。 进一步对影响局部损伤钢压杆弹塑性极限荷载的有关参数,例如FRP加固尺寸、初始缺陷等进行分析。构件尺寸、材料特性、损伤区域大小以及FRP的材料性能与算例1相同。 相对加固长度l′=lf/ld,相对加固宽度b′=b/B,相对加固厚度t′=t/tf。初始缺陷信息一般采用相对最大初始挠度v′和 相对偏心距e′2个参数表示,v′=1 000v0/l,e′=1 000e/l。 4.2.1FRP加固尺寸的影响 对局部损伤偏心受压矩形试件粘贴不同尺寸的FRP进行加固。在v′=1、e′=1、b′=1、t′=1情况下,FRP加固长度对弹塑性极限荷载的影响见表2所列。从表2可知,当l′≤1.0(即lf≤ld)时,x=l1截面先于构件中点发生弹塑性失稳,当l′>1.0(即lf>ld)时,弹塑性失稳发生在构件中点,继续增加FRP的加固长度并不能提高钢压杆的弹塑性极限荷载。因此,在实际加固工程中,FRP加固长度应当覆盖整个损伤区域长度,建议在保证FRP与构件黏结良好的基础上,l′取1.1左右。 表2 FRP加固长度的影响 在v′=1、e′=1、b′=1、l′=1.1的情况下,FRP加固厚度对恢复、增强钢压杆弹塑性稳定极限荷载Fu以及对中点挠度v1的影响情况如图5所示。 由图5a可知,FRP加固厚度对极限荷载的影响较大,加固效果显著。与无损构件相比,纵向粘贴FRP厚度t为1.753 mm(图5a中相对加固厚度t′=2.1),可以恢复损伤构件的弹塑性极限荷载。由图5b可知,FRP加固厚度对中点挠度v1的影响效果有限,说明FRP对钢压杆刚度影响较小。 图5 FRP加固厚度的影响 在v′=1、e′=1、l′=1.1情况下,局部损伤构件采用不同FRP加固宽度进行加固,并使其弹塑性失稳时的极限荷载恰好恢复到无损状态,此时t′-b′关系曲线如图6所示。 加固宽度越小的构件所需的加固厚度越大,但FRP总体用量不变。因此,在实际的加固工程中,建议全宽加固或包裹加固,如图7所示,以减少加固层数,并保证加固工艺及加固效果。 图6 极限荷载恢复到无损状态时的t′-b′关系曲线 图7 2种建议的FRP加固方式 4.2.2 初始缺陷的影响 依据本文计算理论及公式,当钢压杆在中点截面发生弹塑性失稳时,初始挠度及初偏心2种缺陷对构件弹塑性极限荷载等的影响程度完全相同。因此,在下面的分析中,初始缺陷信息用相当初始缺陷v′+e′表示,构件加固方式为采用FRP对损伤区域全覆盖加固,l′=1.1、t′=2.0、b′=1.0保持不变。 仅考虑v′+e′对构件弹塑性极限荷载、中点挠度等的影响,分析结果见表3所列。 由表3可知,初始缺陷对构件弹塑性极限荷载影响明显。 表3 v′+e′对FRP加固后钢压杆弹塑性性能的影响 当初始缺陷逐渐增大时,构件的极限承载力和弹性核高度降低,中点挠度、受拉侧表面应力σt、FRP应力σf逐渐增加。相当初始缺陷v′+e′=10.168时,恰好为单侧出现塑性区与双侧出现塑性区2种情况的分界点。同时,随着初始缺陷逐渐增大,对极限荷载的影响逐渐降低,而FRP发挥的加固效果越来越明显,使FRP加固后的钢压杆承载力逐渐接近并最终超过了无损构件。上述分析结果表明FRP在加固和提高含初始缺陷的局部损伤构件弹塑性稳定性方面具有良好的可加固性和优越性。 本文充分考虑初弯曲和初偏心2种初始几何缺陷的影响,基于Ježek法推导FRP加固局部损伤偏心受压钢压杆绕强轴弹塑性失稳时极限荷载的计算公式。FRP加固方式为对损伤侧进行粘贴加固。通过算例与有限元计算结果对比分析,验证了本文方法的可靠性、解析算法和结论的广泛适用性。 对FRP加固尺寸以及初始几何缺陷等参数进行分析,得到的影响规律如下: (1) 当FRP相对加固长度l′≤1.0时,x=l1截面先于构件中点发生弹塑性失稳,l′>1.0时,弹塑性失稳发生在构件中点,继续增加加固长度并不能提高构件的弹塑性极限荷载。建议在保证FRP与构件黏结良好的基础上,l′取1.1左右。 (2) FRP加固厚度对极限荷载的影响较大,对中点挠度v1的影响效果有限,即对钢压杆刚度影响较小。 (3) 为达到相同加固效果,FRP加固宽度越小所需的厚度越大,FRP总体用量不变。因此,建议全宽加固或包裹加固,以减少粘贴层数、保证加固工艺及加固效果。 (4) 初始缺陷对构件弹塑性极限荷载影响明显。当构件在中点截面发生弹塑性失稳时,初始挠度及初偏心2种缺陷对钢压杆极限荷载等弹塑性性能的影响程度完全相同。初始缺陷越大,构件的极限承载力和弹性核高度越小,中点挠度、受拉侧表面应力σt越大,FRP发挥的加固效果越明显。研究结果表明FRP在加固、恢复甚至提高含初始缺陷的局部损伤钢压杆弹塑性稳定性方面,具有良好的可加固性和优越性。 [1] 王奔,郭小农,蒋首超,等.FRP加固金属结构研究综述[J].结构工程师,2012,28(5):183-190. [2] SEN R,LIBY L,MULLINS G.Strengthening steel bridge sections using CFRP laminates[J].Composites Part B:Engineering,2001,32(4):309-322. [3] MILLER T C,CHAJES M J,MERTZ D R,et al.Strengthning of a steel bridge girder using CFRP plates[J].Journal of Bridge Engineering,2001,6(6):514-522. [4] 任怀胜.FRP复合材料加固钢梁的试验研究和理论分析[D].合肥:合肥工业大学,2009. [5] 马建勋,宋松林,赖志生.粘贴碳纤维布加固钢构件受拉承载力试验研究[J].工业建筑,2003,33(2):1-4. [6] 郑云,叶列平,岳清瑞.FRP加固钢结构的研究进展[J].工业建筑,2005,35(8):20-25. [7] 曹双寅,潘建伍,陈建飞,等.外贴纤维与混凝土结合面的粘结滑移关系[J].建筑结构学报,2006,27(1):99-105. [8] 杨勇新,岳清瑞,彭福明.碳纤维布加固钢结构的黏结性能研究[J].土木工程学报,2006,39(10):1-5. [9] TAVAKKOLIZADEH M,SAADATMANESH H.Fatigue strength of steel girders strengthened with carbon fiber reinforced polymer patch[J].Journal of Structural Engineering,2003,129(2):186-196. [10] 彭福明,郝际平,岳清瑞,等.FRP加固钢结构轴心受压构件的弹性稳定分析[J].钢结构,2005,20(3):18-21. [11] 邓长根,朱文美.碳纤维加固钢压杆的简化稳定分析[J].工业建筑,2008,38(3):106-108. [12] 李斌,李传习,韦成龙.FRP加固局部损伤钢压杆的稳定分析[J].钢结构,2014,29(10):9-12. [13] 杨刚,王海滨,张爱锋,等.碳纤维增强压弯构件弹塑性失稳解析解[J].工程力学,2007,24(5):53-57. [14] 钮鹏.碳纤维增强压弯钢构件稳定性研究[D].大连:大连海事大学,2011. [15] 钮鹏,金春福.几何缺陷影响下的CFRP-方钢管极限承载力解析解[J].工程力学,2015,32(增刊1):322-326. Elastic-plasticstabilityanalysisofeccentriccompressionsteelmemberswithlocaldamagestrengthenedbyFRP LI Bin1, LI Chuanxi2, LUO Hua1, WANG Weiwei1 (1.School of Civil Engineering and Architecture, Hunan Institute of Science and Technology, Yueyang 414000, China; 2.School of Civil Engineering and Architecture, Changsha University of Science and Technology, Changsha 410076, China) Based on Ježek method, the analytical expressions of calculating the ultimate load of buckling of eccentric compression steel members with local damage strengthened by fiber reinforced plastic(FRP) considering the initial bending and initial eccentricity are derived. The correctness and reliability of the analytical formulas is verified using the finite element software. The main factors affecting elastic-plastic capability of steel compression members such as the length, thickness and width of FRP, initial bending and initial eccentricity are discussed. The reasonable reinforcement suggestions and the influence law of the parameters are obtained. The results show that FRP reinforcement has the feasibility and superiority in resuming and improving the elastic-plastic stability of steel compression members with local damage considering initial defects. fiber reinforced plastic(FRP); local damage; eccentric compression steel members; elastic-plastic stability 2016-03-14; 2017-08-17 国家重点基础研究发展计划资助项目(2015CB057701;2015CB057702);湖南省教育厅科研资助项目(16C0725)和湖南省大学生研究性学习资助项目(湘教通[2017]205号) 李 斌(1981-),男,浙江绍兴人,博士,湖南理工学院副教授; 李传习(1963-),男,湖南衡阳人,博士,长沙理工大学教授,博士生导师; 罗 华(1985-),男,湖南岳阳人,博士,湖南理工学院讲师,通讯作者,E-mail:13873065820@163.com. 10.3969/j.issn.1003-5060.2017.12.013 TU391 A 1003-5060(2017)12-1649-06 (责任编辑张淑艳)3.2 未经FRP加固的钢压杆
4 数值分析
4.1 对比验证
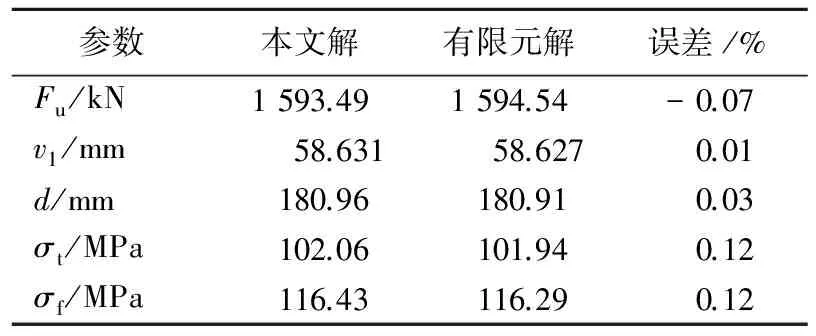
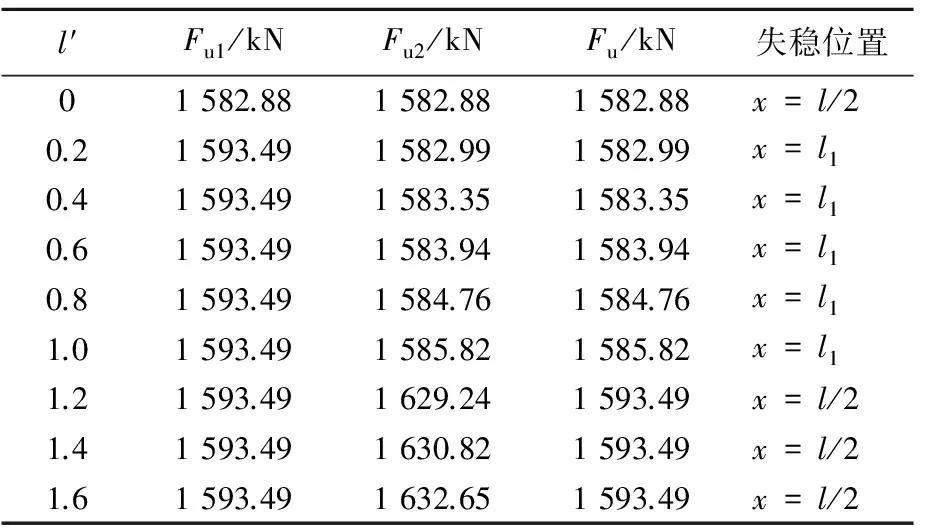
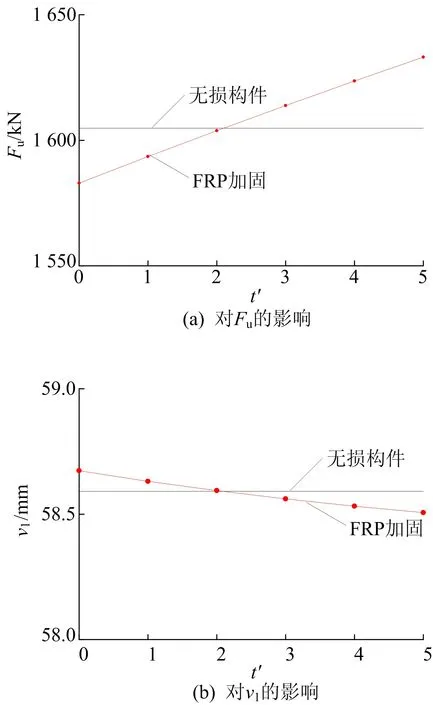
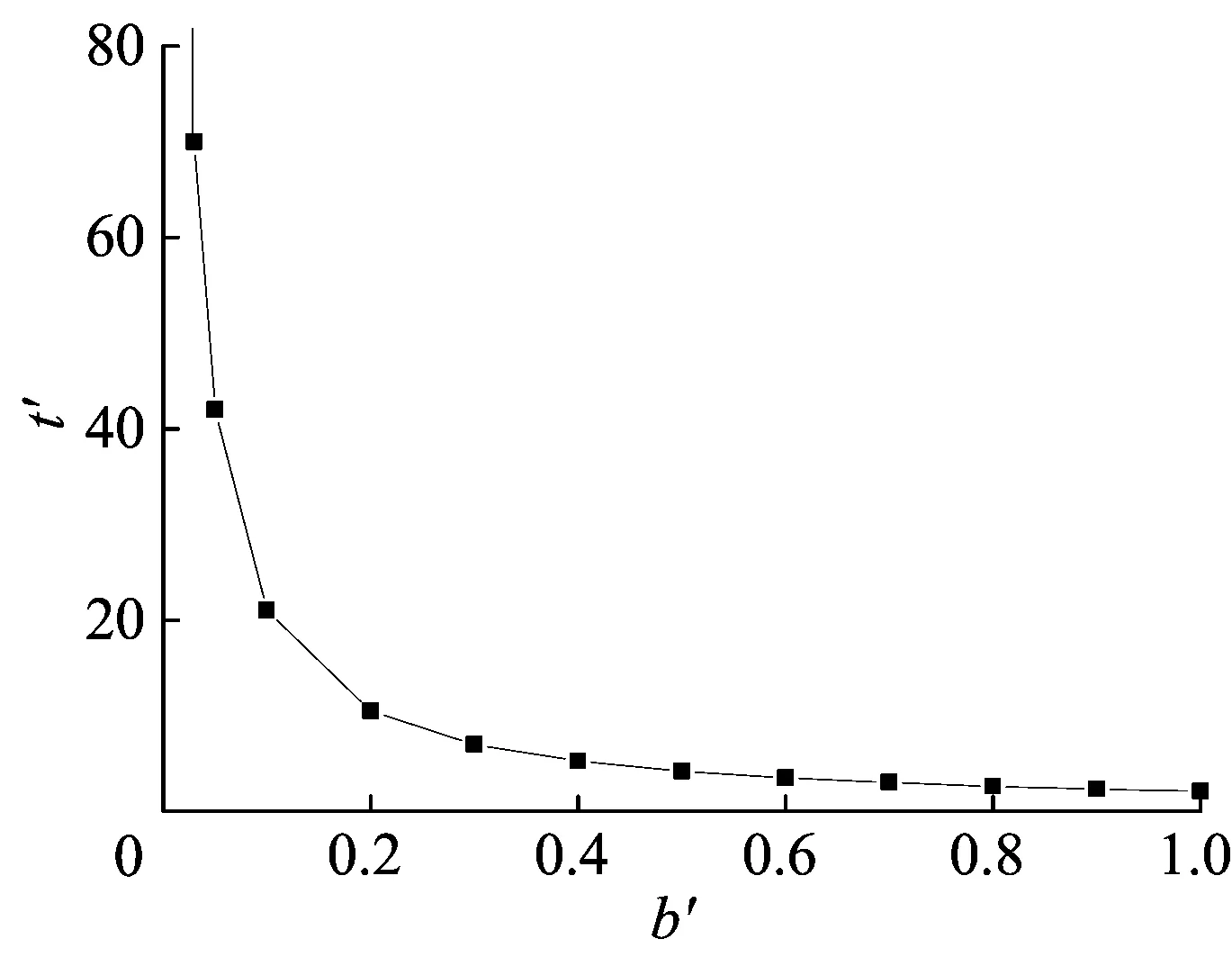
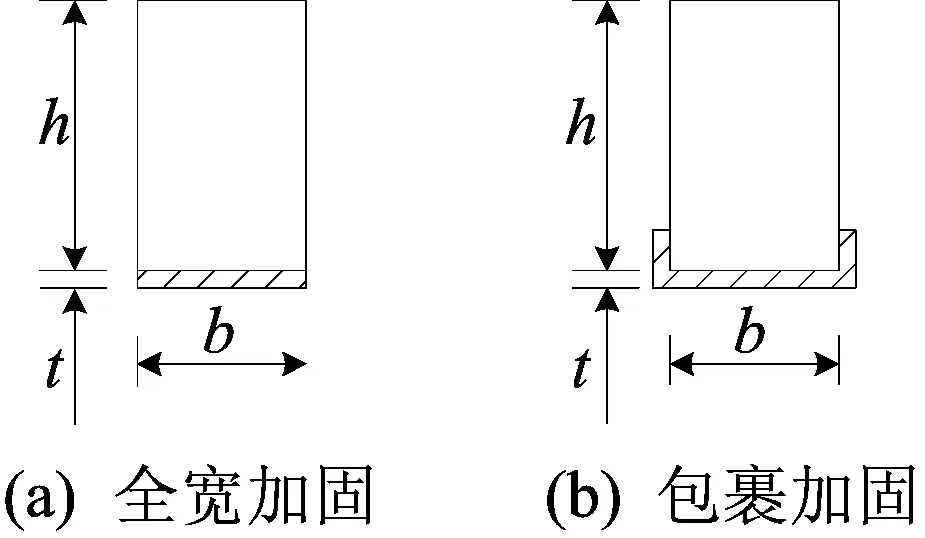
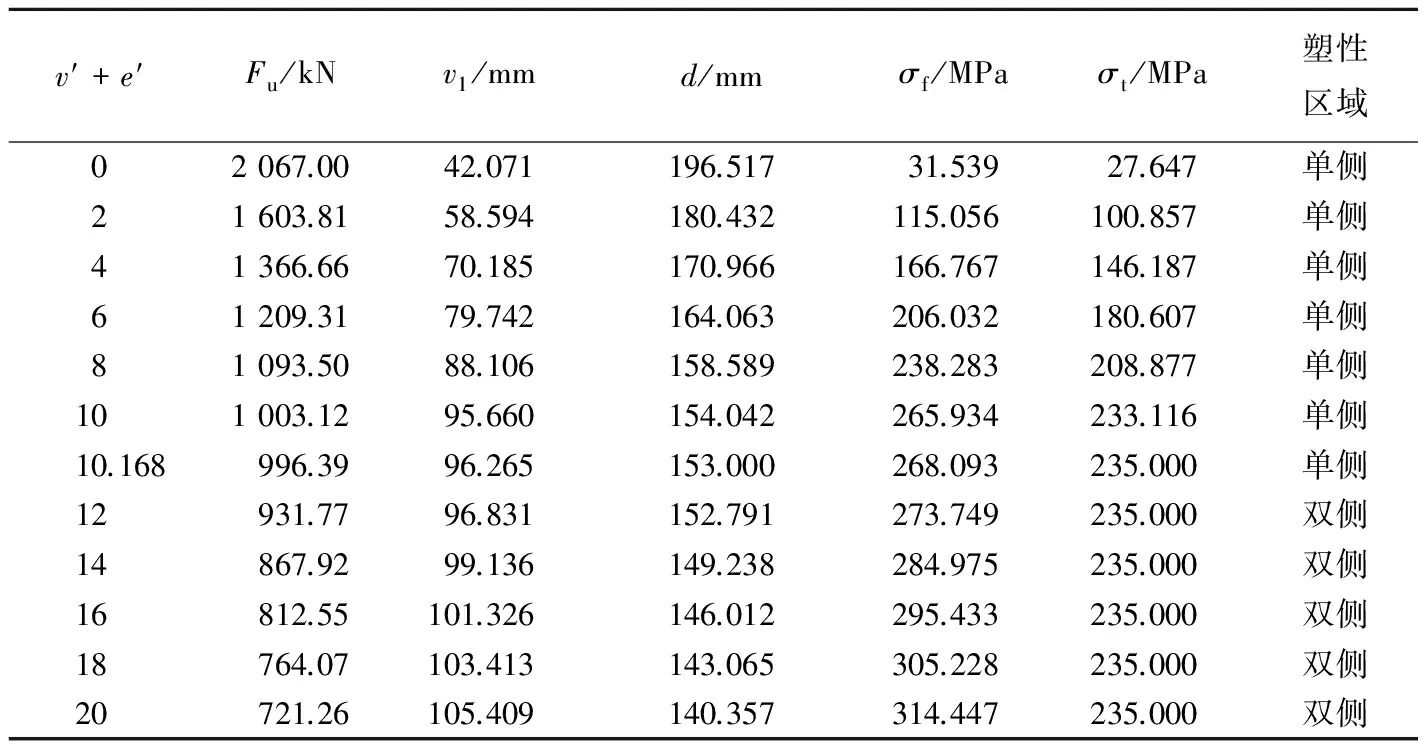
4.2 影响参数分析
5 结 论

