修正的卷积完全匹配层技术
谢国大, 宋开宏, 黄志祥
(安徽大学 电子信息工程学院,安徽 合肥 230039)
修正的卷积完全匹配层技术
谢国大, 宋开宏, 黄志祥
(安徽大学 电子信息工程学院,安徽 合肥 230039)
复频移的卷积完全匹配层(convolutional perfectly matched layer,CPML)与时域有限差分(finite-difference time-domain,FDTD)算法递推公式之间存在数值计算时间不同步的问题,诸多算例结果表明CPML的吸波效果并没有达到一些具有相同二阶精度的完全匹配层(perfectly matched layer,PML)的吸波效果。文章采用时间平均近似方法对CPML进行了修正,使其吸波性能与其他具有相同数值计算精度的PML的吸波性能相当;通过2个具有代表性的算例,验证了方法的有效性。该方法思路简单、清晰,只需在传统的CPML代码基础上进行简单的修改,计算时间大大缩减,该方法对于CPML在FDTD算法中的高效应用具有一定的意义。
时域有限差分(FDTD)算法;卷积完全匹配层(CPML);吸收效果;时间平均近似方法;计算时间
自从Berenger于1994年提出完全匹配层(perfectly matched layer,PML)[1]吸收边界条件以后,PML已经成为有效的吸收边界条件技术,随后一些其他形式的PML也相继被提出来,例如,各向异性完全匹配层(uniaxial perfectly matched layer,UPML)[2]、坐标伸缩完全匹配层(stretched-coordinate perfectly matched layer,SC-PML)[3]等。其中SC-PML成为最受欢迎的一种截断时域有限差分(finite difference time domain,FDTD)[4-5]计算区域的吸收边界条件。这是因为SC-PML不需要进行场分裂,很容易应用到非均匀、色散、各向异性及非线性媒质中。另外,它使得基于伸缩坐标方程的复数频率移位完全匹配层(complex frequency shift perfectly matched layer,CFS-PML)的应用更加方便[6]。CFS-PML是在1996年被提出来的,其目的是为了改善SC-PML对倏逝波和低频波吸收效果差的问题[7]。文献[8]给出了一种应用CFS-PML的方法,该方法基于SC-PML公式,运用离散递归卷积方法来求解复数频率移位函数与电场或磁场的空间偏导卷积运算。由于在SC-PML中的伸缩因子采用了CFS形式,使得在时域公式中出现卷积运算,对应的SC-PML也被称为卷积完全匹配层(convolutional perfectly matched layer,CPML)。CPML与其他一些基于递归积分(recursive integral,RI)[9]方法、Z-变换方法[10]以及辅助微分方程(auxiliary differential equation,ADE)[11]方法的PML都具有二阶精度,因此它们具有可比拟的吸收效果。
然而在一些算例中发现CPML的吸收效果并没有其他一些具有相同二阶精度的PML的吸收效果好[9]。通过对CPML算法深入的调查和研究发现,这与算法本身的数值计算精度无关,而是由于CPML中的卷积与FDTD基本算法递推公式在值的更新时刻上不同步造成的。基于此,本文提出了一种时间平均近似方法来解决CPML与FDTD递推公式之间时间不同步的问题。
1 CPML理论分析
在频域和伸缩坐标中,根据安培定律,三维情况下x方向的麦克斯韦方程为:
其中,su(u=x,y,z)为坐标伸缩因子[2],其计算式为:
应用CFS算法[7],可将(2)式修改为:
其中,σu、αu、ku为非零实数,被定义为u方向的一维数组,控制波在PML层内的衰减速度。
由于(1)式中伸缩因子su(u=x,y,z)与频率有关,过渡到时域时(1)式右端出现卷积运算。
通过调查我们了解到,H社区在进行消防安全巡查工作时,其工作人员本身的技术是有限的,只能进行初步的安全隐患排查,无法达到专业的水准。 由于辖区内商铺众多,有些社区人员只是为了完成指标任务,走马观花,达不到真正防范消防安全隐患的目的。 社区工作人员说道:
其中,*表示卷积。为了得到(4)式中卷积的有效计算表达式,可以将冲击响应ζu(t)离散并定义为:
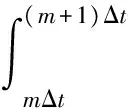
cuexp{-[(σu/ku)+αu](mΔt/ε0)}
(5)
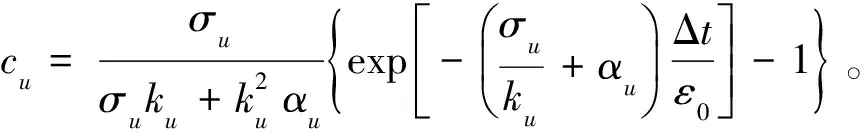
根据(5)式,(4)式可在时间和空间上离散成如下形式:
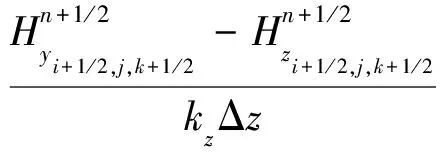
(6)式右端最后2项是由离散卷积导出的求和项,不便于FDTD时域步进计算,而根据文献[8]的离散递归卷积方法可以得到适合FDTD时域步进计算的公式,即
(7)
(8)
(7)式、(8)式中的bu和cu与文献[8]中的形式相同。从(6)~(8)式可以看出,卷积计算发生在0~(n+1)Δt时刻,卷积公式里磁场的空间导数值在nΔt~(n+1)Δt为常数并等于其在(n+1/2)Δt时刻的值。因此,(6)式可以写成如下形式:
从(9)式可以看出FDTD基本公式中电场的时间导数值和磁场的空间导数值的计算发生在(n+1/2)Δt时刻,而卷积值的计算发生在(n+1)Δt时刻,这样在FDTD中每次的时域步进计算中就产生了数值计算时刻不同步的问题。
将(10)式、(11)式代入(9)式,可得:
2 数值算例
算例1 验证通过时间平均近似方法修正的CPML的吸收性能。二维TEz波模型如图1所示,网格尺寸Δx=Δy=1 mm,激励源被放置在二维60 mm×60 mm网格正中心,计算区域大小为40 mm×40 mm,卷积完全匹配层厚度为10 mm。时间步长Δt为0.98倍的Courant极限。

图1 二维数值几何模型
用多项式缩比模型来定义CPML层内的基本参数:
σu(u)=σmax(ρ/d)m
(13)
ku(u)=1+(kmax-1)(ρ/d)m
(15)
αu(u)=αmax(ρ/d)
(16)
其中,ρ为自由空间与PML层、交界面到PML层距离;d为PML层的厚度;m为多项式阶数,m=4;kmax=1;αmax=0.25。激励源的时域形式为:
Ey(t)=-2[(t-t0)/tw]exp{-[(t-t0)/tw]2}
(17)
其中,tw为决定时域波形宽度的参数,tw=26 ps;t0=4tw。观察点设在离PML内层2个网格的距离。
为了计算PML的反射误差,需要建立一个参考区域,该参考区域的网格尺寸与算例1的网格尺寸相同,每个方向的网格数是算例1 的20倍。观察点的相对反射误差计算公式为:
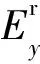
3种PML在观察点的相对反射误差随时间变化的曲线如图2所示。
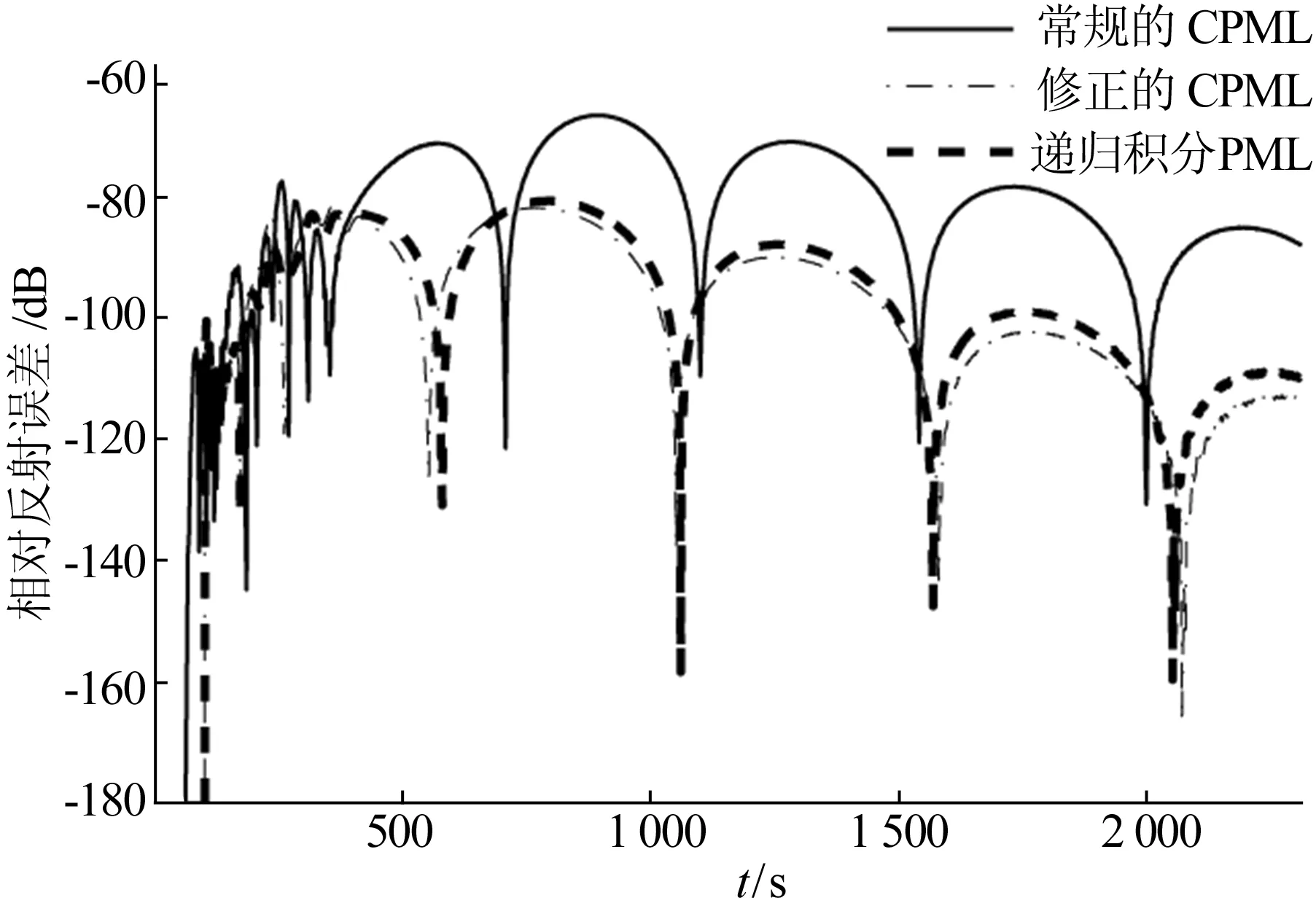
图2 算例1不同PML在观察点的相对反射误差
图2表明修正的CPML比常规的CPML具有更好的吸波性能,同时修正的CPML与递归积分PML吸收效果相当,验证了本文所提方法的正确性。图2说明常规的CPML中存在的不同步问题确实是影响其吸收效果的主要原因,与其CPML自身的数值计算精度无关。
算例2 检验修正的CPML对消逝波的吸波性能。三维数值几何模型如图3所示。
三维模型在x、y、z方向的长度为52 mm×126 mm×26 mm,网格大小为Δx=Δy=Δz=1 mm,完全匹配层的厚度为10 mm,时间步长Δt为0.98倍的Courant极限。金属板置于计算区域的中间且大小为25 mm×100 mm,沿着z方向的激励源被放置在距离金属板上方1个网格的位置,激励源形式与(17)式相同,其中,tw=53 ps,t0=4tw。观察点置于源的斜对角方向并距离金属板1个网格的距离。PML参数为:m=3,αmax=0.2,kmax=1。3种PML在观察点的相对反射误差如图4 所示。图4说明了CPML中存在的时间不同步现象确实影响其吸波性能。
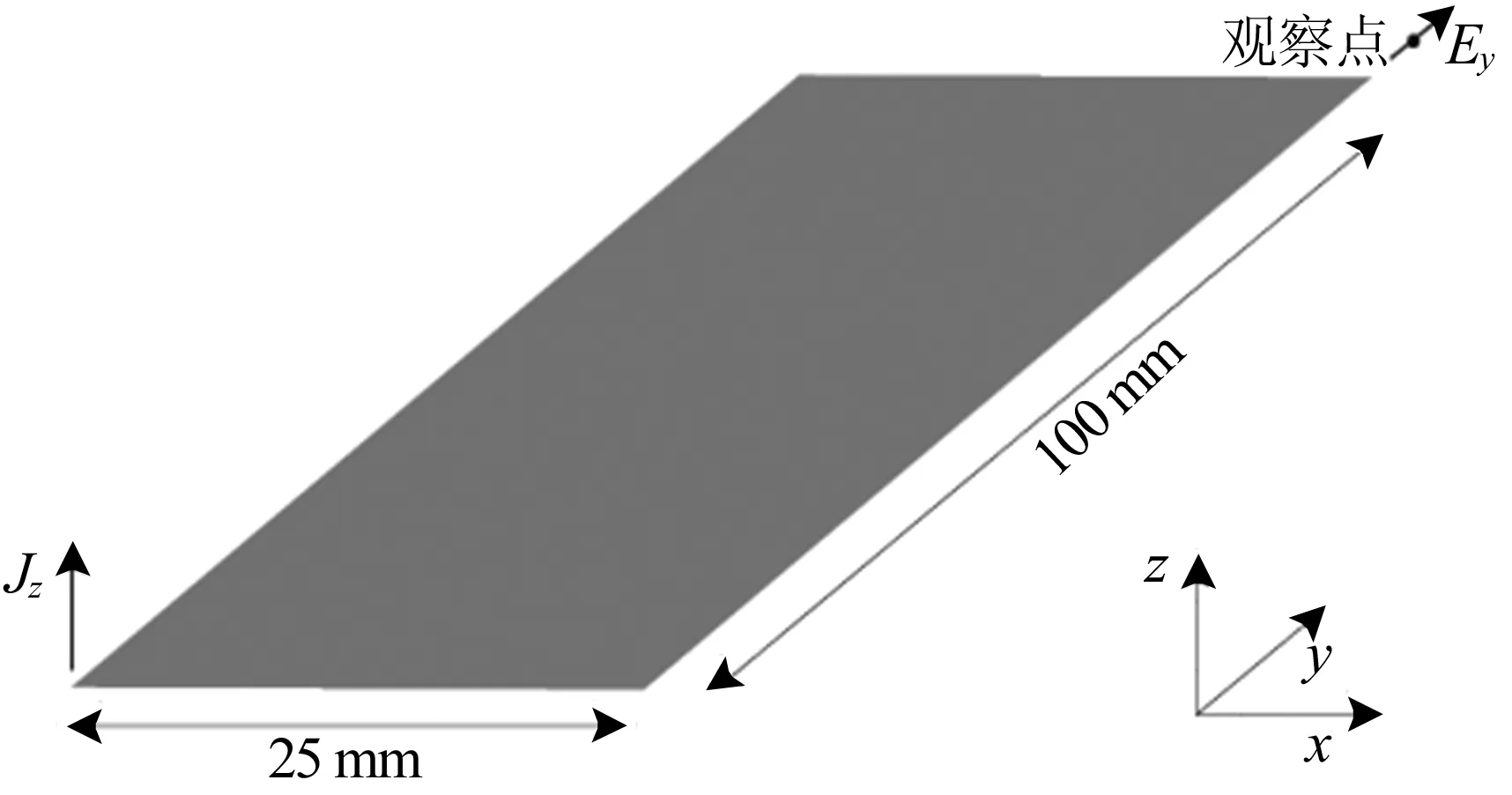
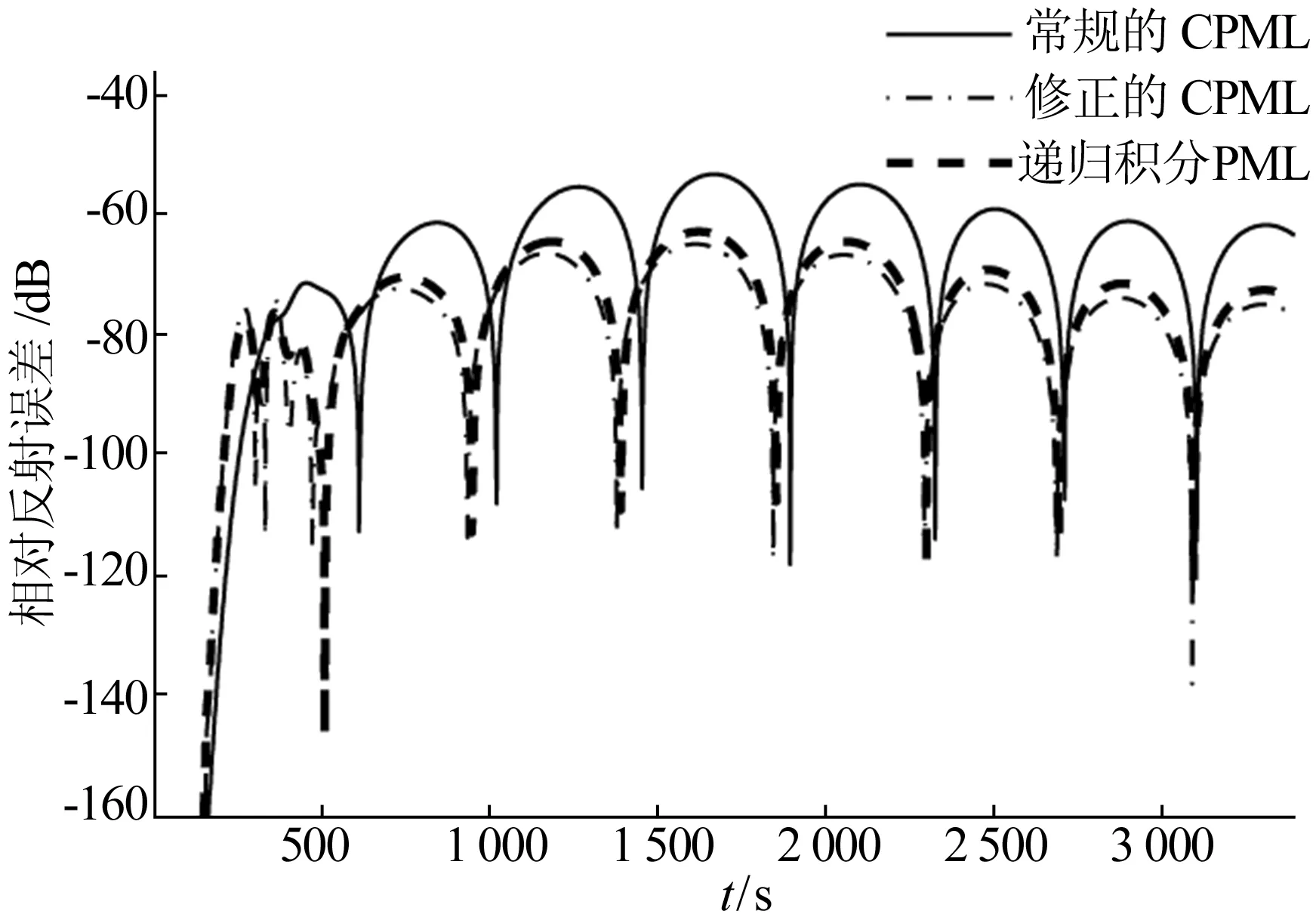
图3 三维数值几何模型图4 算例2不同PML在观察点的相对反射误差
3种方法的计算内存及CPU执行时间(迭代1 600步)对比见表1所列。从表1可知,修正的CPML在计算内存不增加的情况下,其计算时间最短,比传统的CPML计算时间减少了约47%。

表1 3种方法计算内存与计算时间对比
3 结 论
常规的CPML与FDTD之间存在的时间不同步现象对其吸波性能有一定的影响,本文采用时间平均近似方法对CPML进行修正,使其吸波性能与其他具有相同数值计算精度的PML吸波性能相当。该方法简单易于理解,应用时在传统的CPML代码基础上进行简单的修改即可,同时,计算时间大大缩减,为CPML在FDTD算法中的应用提供了重要依据。
[1] BERENGER J P.A perfectly matched layer for the absorption of electromagnetic waves[J].Journal of Computational Physics,1994,114(2):185-200.
[2] GEDNEY S D.An anisotropic PML absorbing media for the FDTD simulation of fields in lossy and dispersive media[J].Electromagnetics,1996,16(4):399-415.
[3] FENG N X,LI J X,ZHAO X M.Efficient FDTD implementations of the higher-order PML using DSP techniques for arbitrary media[J].IEEE Transactions on Antenna and Propagation,2013,61(5):2623-2629.
[4] 葛德彪,闫玉波.电磁波时域有限差分算法[M].3版.西安:西安电子科技大学出版社,2011:99-106.
[5] TAFLOVE A,HAGNESS S C.Computational electrodynamics:the finite-difference time-domain method[M].3nd ed.Boston:Artech House,2005:302-310.
[6] LIU J F,FANF Y,XI X L.A new effective SC-PML implementation for WLP-FDTD method[J].IEEE Microwave and Wireless Components Letters,2015,25(8):499-501.
[7] KUZUOGLU M,MITTRA R.Frequency dependence of the constitutive parameters of causal perfectly matched anisotropic absorbers[J].IEEE Microwave and Guided Wave Letters,1996,6(12):447-449.
[8] RODEN J A,DEDNEY S D.Convolutional PML (CPML):an efficient FDTD implementation of the CFS-PML for arbitrary media[J].Microwave and Optical Technology Letters,2000,27(5):334-339.
[9] GIANNOPOULOS A.An improved new implementation of complex frequency shifted PML for the FDTD method[J].IEEE Transactions on Antennas and Propagation,2008,56(9):2995-3000.
[10] FENG N X,YUE Y Q,LIU Q H.DirectZ-tranform implementation of the CFS-PML based on memory-minimized method[J].IEEE Transactions on Microwave Theory and Techniques,2015,63(3):877-882.
[11] GEDNEY S,ZHAO B.An auxiliary differential equation formulation for the complex-frequency shifted PML[J].IEEE Transactions on Antennas and Propagation,2010,58(3):838-847.
Modifiedconvolutionalperfectlymatchedlayertechnique
XIE Guoda, SONG Kaihong, HUANG Zhixiang
(School of Electronics and Information Engineering, Anhui University, Hefei 230039, China)
The numerical computation time is not consistent between the complex frequency-shifted convolutional perfectly matched layer(CPML) and the recursive formula of the finite-difference time-domain(FDTD) method. It is found that the absorption effect of CPML does not reach the absorption effect of some perfectly matched layers(PMLs) with the same second-order accuracy in many numerical examples. In this paper, the time average approximation method is applied to modifying the traditional CPML, making sure that its absorption effect nearly has the same performance with other PMLs which have the same numerical accuracy. The validity of this method is verified by two representative examples. The presented method based on the simple modification to the traditional CPML code can greatly reduce the computation time, which is of significance for the efficient application of CPML in the FDTD algorithm.
finite-difference time-domain(FDTD) algorithm; convolutional perfectly matched layer(CPML); absorption effect; time average approximation method; computation time
2016-09-28;
2017-09-03
国家自然科学基金资助项目(61471001;51277001)
谢国大(1991-),男,安徽亳州人,安徽大学博士生;
宋开宏(1969-),男,安徽合肥人,安徽大学副教授,硕士生导师,通讯作者,E-mail:sk-hong@sina.com;
黄志祥(1979-),男,安徽合肥人,博士,安徽大学教授,博士生导师.
10.3969/j.issn.1003-5060.2017.12.027
O441.4
A
1003-5060(2017)12-1725-05
(责任编辑张淑艳)

