土壤斥水性影响土壤水分运动研究进展

王秋玲，施凡欣，刘志鹏，熊云武



土壤斥水性影响土壤水分运动研究进展

王秋玲1，施凡欣1，刘志鹏2※，熊云武3

（1. 阜阳师范学院物理与电子工程学院，阜阳 236037；2. 南京农业大学资源与环境科学学院，南京 210095； 3. 中国农业大学水利与土木工程学院，北京 100083）

土壤斥水性广泛存在于各类土壤，是影响植物生长、土壤水分运动以及土壤侵蚀等水土过程的重要因素。该文阐述了土壤斥水性的基本概念，介绍了几种常用的斥水性强度测定方法及适用范围。在此基础上，论文对土壤斥水性如何影响土壤水力性质以及水分运动特征等研究现状作了全面评述，重点讨论了近年来该领域的研究热点，如土壤斥水性影响下的指流观测和理论模拟以及斥水性土壤蒸发过程等。最后，提出了相关研究中亟待解决的若干关键科学问题，主要包括确定土壤斥水性影响指流现象和蒸发过程的物理机制的揭示；考虑土壤斥水性参数的土壤水分运动数学模型的构建；以及对新模型的求解及对数值解的理论分析。由于土壤斥水性对土壤水分运动有重要的关联效应，相关问题的深入研究对进一步认识土壤水分运动的内在物理机制具有重要理论意义，也将为掌握和有效利用土壤斥水性提供实践指导。

土壤；水分；蒸发；土壤斥水性；土壤水力性质；指流

0 引 言

早在19世纪，人们就注意到森林里的蘑菇群或原野上的草坪会出现一种神秘的环形圈，沿圈植物长势格外茂盛，而圈内外则明显较差，人们称之为“仙人圈”。后来人们发现，“仙人圈”的形成与土壤的某种物理性质有关。圈内放射状生长的菌丝或草本植物所形成的斥水有机物使表层土壤很难被水湿润，降雨时雨滴不能入渗土壤而富集到边缘环状区域，使得环状区域的植物生长格外茂盛[1]。土壤颗粒表面不能或很难被水分湿润的物理性质称为土壤斥水性，具有斥水性的土壤称为斥水性土壤[2]。斥水性土壤并非少数特定环境下的特殊存在，它可以在不同土壤质地、土地利用方式和气候条件下广泛存在，世界各地均有关于土壤斥水性的报道[3-7]。Tillman等[8]还发现，即使通常认为的亲水性土壤，当干燥至低于某一临界含水率时，也会表现出一定的斥水性。Tillman指出，土壤斥水性是土壤的一种常态性质，即大部分土壤既非完全斥水，也非完全亲水[8]。

土壤斥水性影响土壤水力特性，对包气带甚至地下水的大范围物理过程具有直接或潜在的影响。主要体现在：1）斥水性土壤入渗能力较低，表层易积水，易产生地表径流和坡面径流，降雨较大时易形成大小细沟，加速土壤侵蚀过程，引起土壤质量退化[9-11]； 2）水分入渗时容易产生不稳定和不规则的湿润锋，入渗常常通过指流等优先流完成，导致土壤水分的不均匀分布，引起养分流失，加快农业化学物的淋洗，增加了地下水污染[9-12]； 3）抑制土壤蒸发，极大地影响田间土壤水分循环[9,13]。因此，土壤斥水性研究不仅涉及土壤科学，而且与生态、水文、地质、微生物和环境等学科密切相关，研究土壤斥水性有助于人们提高农业生产效率、促进资源环境的可持续性发展。

自20世纪60年代以来，有关土壤斥水性的研究一直是土壤学研究的热点[9-10]。国内自从杨邦杰等首次阐述土壤斥水性的概念及由此引起的土壤退化问题以来[2]，开展土壤斥水性相关的研究团队逐渐增多。针对中国土壤，商艳玲等[14]开展了再生水灌溉对土壤斥水性的影响研究，杨昊天等[15]对腾格里沙漠土壤斥水特性开展了研究、孙琪琪等[16]发现沂蒙山区桃园和玉米地棕壤斥水性表现强烈，以及郭成久等[17]对黄土高原苔藓结皮斥水性的研究等。这些相关研究表明，斥水性土壤在中国同样广泛存在。然而，现阶段中国有关土壤斥水性的研究方向还比较分散，系统的研究还比较少，尤其是土壤斥水性相关的指流理论模拟研究方面，国内文献中较少出现。本文在总结国内外斥水性土壤水分运动研究基础上，重点阐述土壤斥水性影响指流研究中涉及的相关物理问题，有望为中国斥水性土壤相关研究的深入开展提供一定参考。

1 土壤斥水性强度的表征

土壤斥水性强弱的表征方法主要有滴水渗透时间法、酒精液滴摩尔浓度法和进水阈值法等，通过定量测量土壤斥水的持久度、强烈度或使水分入渗土壤所需施加的正水压等来作为衡量土壤斥水强弱[18-19]。以上3种方法简单实用，被广泛应用于土壤分类等定性研究中。如试验上常采用的土壤斥水性分类标准[9-10]，即是根据滴水渗透时间法测量的滴水渗透时间将土壤斥水性分为5个等级：不斥水（<5 s），轻微斥水（5～60 s），强烈斥水（60～600 s），严重斥水（600～3 600 s）和极端斥水（>3 600 s）。一般情况下，以5 s作为斥水与不斥水的分界线。

上述方法虽然能够简单直观地表征土壤斥水性强度，却不适合用于理论模拟研究。在理论模拟研究时，一般采用水-固界面接触角（）这一物理参数来表征土壤的斥水强度。90°的土壤可定义为斥水性土壤；反之，则称为亲水性土壤。试验上测量土壤接触角参数的方法主要有固着滴液法[20]和毛管上升法[21]等。固着滴液法是由Bachmann等[20]提出的，将双面胶的一面粘在显微镜载玻片上，将过筛的土壤颗粒均匀地压在双面胶的另一面，形成一层均匀土壤颗粒层。在室温（20 ℃）下用显微镜和量角器测出滴水后颗粒层-水的接触角的值。毛管上升法是则是分别测量水和参照液体（如酒精）在测量土壤中的毛管上升高度，分别对2种液体应用毛管上升公式[21]

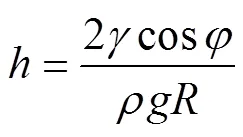
式中为表面张力系数，为液体密度，为重力加速度，为等效毛管半径。在参照液体接触角已知的情况下，如酒精的接触角可视为0°，通过比值法消去试验中很难测定的等效半径，求得水对测量土壤的接触角

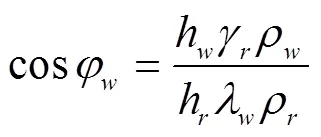
式中下标和分别代表水和参照液体。

无论是固着滴液法还是毛细上升法所测定的接触角均是宏观意义上的接触角，称为等效接触角φ。这与表面物理中常常用来表征材料表面亲疏水性质的接触角概念不同，表面物理中的接触角通常指的是内禀接触角φ，只具有微观意义。等效接触角φ不仅与内禀接触角φ有关，还与土壤孔隙的几何形状有关[22-24]。研究发现，由于土壤孔隙几何形状的非均匀性，当内禀接触角φ为50°左右时，相应的等效接触角φ往往已经大于90°，即已属于斥水性土壤[22,24]；而通常认为完全亲水的土壤（φ<5°），相应的等效接触角也不能忽略。Aminzadeh等[25]应用毛管上升法测得完全亲水性沙土的等效接触角φ介于30°～35°之间。这些结果进一步证实了Tillman所指出的大部分土壤都会表现一定的斥水度，即斥水性是土壤的一种常态[8]。

2 土壤斥水性对土壤水分运动的影响

土壤斥水性对土壤水分运动过程具有重要影响，使得其中的水分入渗、再分布以及蒸发过程均与亲水性土壤明显不同。

土壤斥水性降低土壤渗透系数，降低土壤导水能力，这是斥水性对土壤水分运动影响的最明显特征。DeBano[26]对比了加热后具有斥水性的土壤与未加热的亲水性土壤的水平和垂直入渗，发现斥水性土壤的水平稳定入渗率仅有亲水性土壤的二十五分之一；Wallis等[27]报道斥水性土壤稳定入渗率仅有相邻地块亲水性土壤的六分之一，而且在测量的前5 min，斥水性土壤的最大导水率仅有不到亲水土壤的1%。由于斥水性土壤中水分入渗受到阻滞，土壤表面很容易积水，当降雨充分时，斥水性土壤比亲水性土壤更易出现地表径流和坡面径流。Hosseini等[28]报道了火灾后土壤变得斥水的松树林地表径流增加，导致土壤中的氮磷流失严重。值得注意的是，土壤的斥水性与土壤湿润状况密切相关，土壤湿润后斥水性强度普遍降低[29]。Ritsema和Dekker研究了德国北部的一块斥水性田地土壤斥水性随季节的变化关系，发现干燥季节里将近90%的表层土壤表现出明显斥水性，而湿润季节仅有30%的较深层土壤表现出斥水性[30]。因此，土壤斥水性导致的土壤入渗能力下降这一影响，在较长的干旱周期内会更为明显。Burch等报道澳大利亚尤加利林地土壤在旱季时入渗率仅有0.75～1.9mm/h，而雨季时则有7.9～14.0mm/h，入渗率相差10倍[31]。

土壤斥水性不仅使土壤入渗能力降低，还容易引起非均匀入渗。在非均质土壤中，如土壤基质存在大孔隙、裂隙、根孔、动物洞穴等，水分入渗是湿润锋往往绕过大部分土壤基质仅沿一些优势通道运动，形成优先流。尽管优先流并不仅局限于斥水性土壤，但土壤斥水性会阻滞或延迟水分向土壤基质入渗，从而迫使水流借助大孔隙、裂隙等优先通道运动，从而加剧优先流的形成。如1993年3月在荷兰的一场降雨量达75 mm的大雨后，Ritsema等在斥水土壤中观测到非均匀渗润的优先流现象，而临近的亲水性土壤中则是均匀的入渗模式[32]。他们还发现，当斥水性土壤表面覆盖薄层亲水性土壤时，水流往往先在表层土壤中形成横向径流，进而通过优先流穿透下层斥水性土壤[33]。在均质土壤中，土壤斥水性使水分入渗时容易产生不稳定和不规则的湿润锋，进而形成“指流”[34-37]。Wallach等采用化学处理的方法调节供试土壤的接触角参数，进行了一系列不同接触角土壤在二维玻璃平板夹层中间的点源和面源入渗试验[34-36]。结果表明，当接触角较小时（如48°），土壤湿润区域呈现圆形结构的典型稳定入渗特征。当土壤接触角增大到56°时，土壤湿润区域呈现出明显的指流入渗特征。Annaka等在干燥沙土中进行的非积水入渗试验中，也发现当接触角大于72°时土壤入渗通过指流模式进行[37]。这一结果也说明单纯地用土壤接触角大于90°这一标准来判断土壤斥水性与否有待商榷，也进一步印证了非零固液接触角在影响土壤水分运动中扮演的不可忽视的作用。

有关斥水性土壤蒸发的研究相对较少，但研究结果较一致，即均发现土壤斥水性对土壤蒸发具有不同程度的抑制效应。Bachmann等对不同斥水性强度的砂土分别进行了等温及非等温条件下的土柱蒸发试验，试验结果表明，两种条件下的土壤累积蒸发量均随土壤斥水性强度的增加而降低[38]。李毅等进行了覆膜开孔条件下斥水性层状土壤蒸发试验，结果表明随着土壤斥水性强度增加，累积蒸发量有所减小[39]。Gupta等利用土壤斥水性抑制蒸发的原理，在亲水性土壤表层覆盖斥水性土壤薄层，达到降低水分散失的目的。他们的对比试验结果表明，表层覆盖2 cm厚的斥水性土壤薄层，即可让下层亲水性土壤保持90%的含水量达83 h[40]。Rye等在田间试验土箱中进行的原位测量，结果表明4 d内斥水性土壤的累积蒸发量比亲水性土壤低40%～80%[13]。

3 土壤斥水性对土壤水力特性的影响

斥水性直接影响土壤孔隙的毛管作用力，使得斥水土壤的水力特性与一般亲水性土壤有很大差异。Wang等应用非正弦毛细管束模型模拟土壤结构，研究了土壤接触角对土壤水分特征曲线的影响[22]。正弦毛细管束模型中，土壤孔隙结构被描述为周期性变化的正弦毛细管，孔径函数为

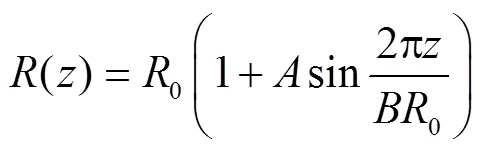
其中为孔隙半径，沿水分入渗方向的位移坐标，0为基础半径，为孔径变化振幅，为变化周期。根据Laplace定理，半径为的毛细管对应的毛细力为

其中，φ=φ+φ；φ为等效接触角，(°)；φ为内禀接触角，(°)；φ为由毛细管壁非均匀性引起的接触角增加。从公式（4）可以看出，土壤接触角是决定土壤毛管吸力的重要参数，非零接触角与土壤微观孔隙非均匀性的耦合作用将进一步放大土壤的滞后效应，使斥水性土壤阻滞水分运动效应更为明显。这一结论与Czachor等的模拟结果[23]和Bauters等的试验结果一致[41]。图1为Bauters等通过混合土壤法获得不同斥水强度土壤，分别测量的不同斥水度土壤在湿水/脱水过程的水分特征曲线（如图1所示）。从图1a可以看出，土壤斥水性对土壤水分特征曲线的吸湿曲线影响显著，斥水性强度增加，同等含水量对应的土壤毛管吸力增加，当接触角大于90°时，毛管吸力由普遍的负值转为正值；而图1b中不同斥水性强度土壤的曲线基本重叠，表明斥水性对特征曲线的脱水分支影响很小。

值得注意的是斥水性土壤的进水阈值h在水分特征曲线的位置与亲水性土壤不同。进水阈值对应的是土壤基质中孔径最大的孔隙所具有的毛管吸力（斥力或吸力）[42]。斥水性土壤中，进水阈值等于吸湿曲线中空气含量接近饱和端的拐角处（图1a的A点）的压力值，且h>0表明需施加一个正水头迫使水分进入土壤。对<90°的亲水性土壤，孔径最大的孔隙最后开始进水，进水阈值等于脱湿曲线中水分含量接近饱和端的拐角处（图1a的B点）的压力值，且h<0，表明负压状态下水分即可进入土壤孔隙。

图1 不同斥水强度土壤的水分特征曲线（试验数据取自文献[41]）

土壤斥水性不仅影响土壤毛管吸力大小，还影响土壤入渗时水分进入孔隙的先后顺序，使得斥水性土壤的非饱和导水率曲线对土壤含水量的响应关系也与亲水性土壤有很大区别。土壤主要通过水分充填的孔隙导水，因此土壤的非饱和导水率主要取决于水分充填部分孔隙所占总孔隙度的比例[42]。亲水性土壤基质势起吸水作用，孔径越小的孔隙吸力越强，水分入渗时首先进入孔径较小的孔隙；与之相反，斥水性土壤基质势起斥水作用，孔径越大的孔隙排斥力越小，水分入渗时先进入孔径较大的孔隙。土壤含水量较低时，亲水性土壤中水分首先被分配给孔径最小的部分孔隙，起导水作用的通道孔径较小，由于导水率与孔径的平方成正比，此时土壤导水率也较低。随着土壤含水量增加，较大孔径的孔隙被水分充填并参与导水，土壤导水率迅速增加，研究发现导水率随含水量增加呈指数递增。斥水性土壤中，孔径越大的孔隙越早被水分充填。土壤水量较低时，水分首先被分配给孔径较大的部分孔隙，起导水作用的通道孔径较大。因此在低含水量条件下，斥水性土壤的导水率比亲水性土壤的要高。随着含水量的增加，较小孔径的孔隙被水充填并参与导水，土壤导水率随之增加，但增加速度较亲水性土壤要慢得多。DiCarlo等测量了原油污染的斥水性土壤的导水率曲线，发现其非饱和导水率随含水量增加呈线性递增，比亲水性土壤的指数递增要慢的多[43]。另外，相同土壤含水量条件下，斥水性土壤在吸湿和脱湿过程的导水率也不同，这也是由于不同过程水分充填起导水作用的孔隙不同引起的。Diamantopoulos 等对比研究了不同斥水性强度土壤在吸湿和脱湿2个动态过程的导水率曲线，发现随着土壤斥水性强度的增加，土壤导水率曲线的滞后效应越发明显[44]。

4 土壤斥水性影响土壤水分运动模拟研究

4.1 土壤入渗模拟

准确模拟并预测斥水性土壤水分运动在农业生产和环境保护中具有重要意义。然而，斥水性土壤水分入渗时经常发生的指流现象及其特征，给经典的多孔介质水分运移理论带来了巨大的挑战[45-47]。

DiCarlo[48]应用光透射法测量土壤剖面含水率分布时发现，紧随湿润锋后的“指尖”含水率较高甚至接近饱和，而上方的“指尾”含水量较低（如图2b）。这种土壤含水量分布沿入渗深度在“指尖”处呈现凸起的现象被称为非单调性饱和度分布（如图2b所示）。指流的这一特征与经典土壤水分运动方程描述的稳态流的土壤含水量随入渗深度增加单调递减的现象明显不同（如图2a所示）。另外，Gerger等[49]测量入渗过程的毛管吸力分布时发现，指流发生时伴随非单调性饱和度分布的还有毛管吸力分布的非单调性凸起，由此产生的压力梯度反转使得湿润锋不稳定，很容易分裂成数个“指状”前锋，并不断发育推进。具有这种非单调性特征的水分入渗也被称为“非稳态流”。科学解释非稳态流的非单调性特征，对探明指流发生机制至关重要。

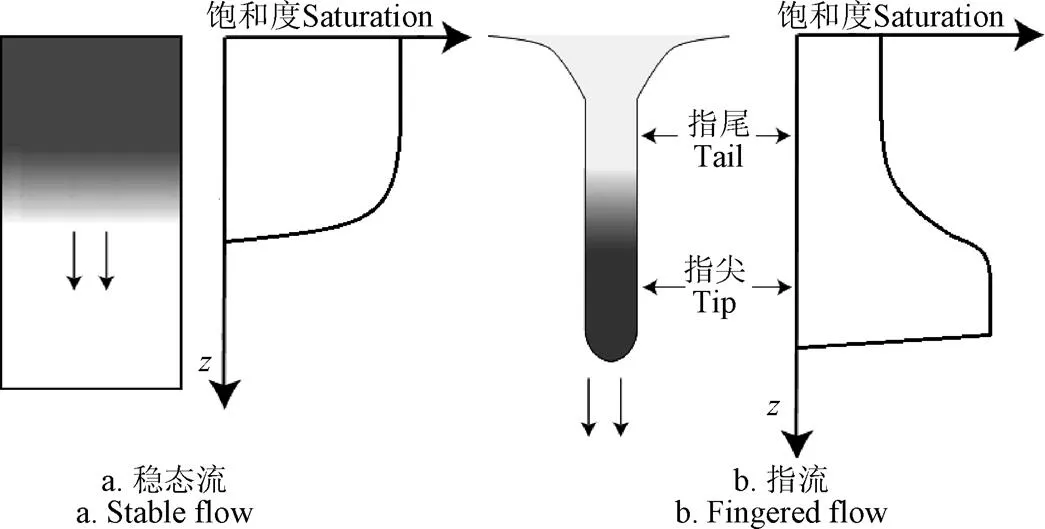
图2 均匀入渗和指流的饱和度分布示意图

经典的多孔介质水分运移理论Richards方程，是一种基于连续介质假设的理论模型。Richards方程在模拟均匀入渗时取得了巨大成功，被广泛应用于各种土壤的饱和及非饱和入渗过程的模拟。Richards方程是基于白金汉-达西定理和连续方程建立的偏微分方程，即

其中为土壤含水率，为土壤基质势，()为土壤非饱和导水率，为时间，为坐标。在给定的土壤水力特性（土壤特征曲线()和导水率曲线()或()）条件下，结合初始条件和边界条件，数值求解方程（5）可获得土壤含水率的时空分布(,)。

然而，研究发现，Richards方程的双曲型特性决定了方程（5）在给定土壤的单调性()关系前提下只能给出单调性解，与指流饱和度分布的非单调性特征明显不符，因此不能用于描述指流现象[50]。人们尝试了各种方法修正Richards方程。Eliassi和Glass提出“阻滞-堆积效应”这一物理概念[51]，认为流体的某种物理性质会轻微阻止水分进入干燥孔隙内，宏观效果上就导致湿润锋前进被阻滞,而后续输运的水分只能在湿润锋后形成堆积，这种堆积效应形成了较高含水量的“指尖”区域。为此，人们提出多种物理机制解释湿润锋被阻滞的原因，如Hilpert等提出的动态接触角机制[52-53]，Hilfer等提出的毛管滞后效应[54-55]等。与这些物理机制相对应，需要在Richards微分方程中增添一定的高阶项。修正后的Richards方程在某些条件下能够模拟指流的饱和度凸起特征，但是不足之处在于引入了过多的经验参数，而这些参数值往往偏离实验允许的合理范围。

除修正的Richards方程外，Cueto-Felgueroso和Juanes将曾在模拟二维流室中粘滞力驱动的指流时取得成功的相场理论应用于非饱和土壤入渗过程，建立了四阶偏微分方程[56]，即

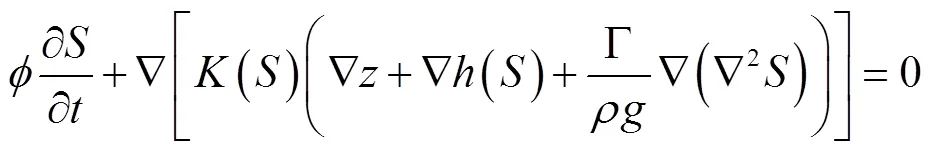
除连续模型外，人们还尝试应用其他非连续模型来模拟指流。Dicarlo等[57]应用网格模型，结合微观孔隙尺度上的“活塞式”和“阶跃式”2种孔隙水分充填机制，对石英砂介质入渗过程中的水饱和度分布进行了模拟。但他们的模型对所有供水率条件都给出饱和度凸起，这与试验观测到的饱和度凸起仅在某些供水率范围内出现的结果不一致。为此，人们在网格模型的基础上考虑各种细微效应，比如考虑粘滞力引起压力消减的动态网格模型等[58]。但模型预测结果与试验测量值之间仍有较大差距。

除上述以土壤水力特性为输入参数的数学物理模型外，Xiong等应用矩分析法模拟斥水性土壤中的非稳态水分运动，使用湿润区中心距和二阶矩这2个变量随时间的变化特征，定量描述亲水土壤和斥水土壤的水分垂直入渗过程[59]。模拟获得的斥水性土壤湿润区的二阶距随时间变化曲线能够较好反应出实验观测到的湿润区边缘含水量急剧降低、湿润锋后的饱和度凸起等非稳态流特征，表明矩分析法在定量描述斥水性土壤水分运动过程具有一定有效性。此外，他们还尝试应用人工神经网络模拟亲水性土壤和斥水性土壤的水分运动过程[60]，进行了3种人工神经网络模型（self-organizing maps，SOM；multilayer perceptrons， MLP 和modular neural networks， MNN）的模拟应用研究，发现后2种人工神经网络模型可以通过预测湿润区域的空间矩，获得具有非稳态流特征的模拟结果。

4.2 土壤蒸发模拟研究

土壤蒸发过程的模拟研究，主要有连续介质模型和非连续介质模型2类。前者主要见杨邦杰等[61]和Bachmann等[38]的研究，两者都是基于Philip-de Vries理论建立水热耦合运动控制方程，数值求解偏微分方程获得蒸发率和累积蒸发量，这方面工作李毅等[62]已作详细介绍，本文不再赘述。

非连续介质模型主要是基于侵入渗流理论（IP invasion percolation）的网格模型。Chapuis和Prat[63]应用二维方形孔道构成的网格模拟多孔介质孔隙结构，在侵入渗流理论基础上考虑接触角参数对孔隙充填机制的影响（如表1所示），数值模拟了不同接触角参数条件下的蒸发过程。模拟结果表明，亲水性介质的干燥时间远小于斥水性介质。

表1 不同接触角参数范围适应的孔隙充填机制

无论试验观测还是理论模拟，研究结果均表明土壤斥水性抑制土壤水分蒸发，但土壤斥水性如何抑制土壤水分蒸发的物理机制尚未明确。Lehmann等[64]应用基于IP理论的三维网格模型模拟研究多孔介质干燥过程特征，发现干燥特征长度对累积蒸发量具有重要影响。Shokri等[65]比较了亲水性和斥水性均匀土柱蒸发试验，发现斥水性土壤的特征干燥长度仅17 mm，而亲水性土壤则达到130 mm。试验初始斥水性土壤的干燥锋深度未达到特征长度之前，2种土壤的累积蒸发量相近；当斥水性土壤的干燥锋深度达到17 mm后，斥水性土壤稳定蒸发阶段结束，蒸发率迅速下降。与之相反，亲水性土壤的稳定蒸发阶段一直持续至干燥锋到达130 mm深度，因此亲水性土壤的累积蒸发量远高于斥水性土壤。基于这一结果，Shokri等[66]进一步提出，土壤中斥水性颗粒的存在使得附着在土壤颗粒表面的薄膜水减少，降低了土壤孔隙内水分分布的连续性，切断了深层水分通过毛管吸力向上输运的连续通道，水分输运只能通过扩散作用完成，蒸发过程由稳定蒸发阶段转为蒸发率持续下降阶段。由这一猜想出发，Shokri等应用团簇模型，考虑不同比例的斥水性和亲水性团聚体组成的团簇，计算团簇的等效接触角，并根据毛管吸力与重力相平衡原理，计算不同组分团簇的特征干燥长度，计算得到的特征干燥长度值与试验测量值相符。然而，Kim等[67]将混合后的亲水性和斥水性砂土进行X-射线扫描，结果却显示亲水性沙土附着的水膜已足够保持水力通道的连续性，使得干燥锋进一步推进。因此土壤斥水性对土壤蒸发过程的影响机制，还有待更多的研究。

5 总结

综上所述，尽管学术界对土壤斥水性的研究已有近百年的历史，大量科学家从不同角度探索了其发生物质来源，建立了多种定性定量地表征土壤斥水性强度的方法，并揭示了土壤斥水性对土壤水分运动的重要影响。然而，由于土壤结构的复杂性，微生物、有机质、气候、温度和土壤含水率等都对土壤斥水性有显著影响，且土壤斥水性具有高度的时空异质性，有关土壤斥水性特征、斥水性土壤水分运动及模拟方面的研究中仍存在许多亟待解决的问题：

1）需要进一步明确斥水性对土壤水力性质的影响机理，并建立包含土壤斥水性参数（接触角）的土壤水力性质函数模型。土壤水力性质不仅与土壤孔隙结构相关，也与土壤斥水性密切相关。然而，现有的土壤水力性质函数模型（如van Genuchten模型、Brooks-Crey模型等）均不包含表征土壤斥水性的参数，不能直接反映土壤斥水性对土壤水力性质的影响。通常的处理方法是忽略土壤斥水性的作用，即认为土壤水力特性仅由土壤孔隙结构决定。这种处理方法容易低估斥水性对土壤水分运动的影响。特别是对一些具有较强斥水性的土壤，容易导致模型预测与实际情况出现较大偏差。

2）土壤斥水性影响土壤水分入渗、再分布及蒸发过程的物理机制仍不明确。目前描述土壤水分运动的理论模型都是以土壤水力特性（如土壤水分特征曲线、非饱和土壤渗透系数曲线等）作为模型输入条件。然而，斥水性土壤与亲水性土壤的水力特性具有本质区别，且土壤水力特性函数并不包含土壤接触角参数，这些模型不能用来模拟斥水性土壤中的水分运动过程。因此，需要从微观孔隙尺度的物理过程着手[68-70]，借助恰当的尺度上升模型，结合理论预测与试验观测，探明土壤斥水性影响水分运动的作用机制，并建立包含土壤斥水性参数的水分运动理论模型，进而定量分析土壤斥水性对水分运动过程的影响。

3）预测指流发生并定量描述和模拟指流现象一直是土壤物理学领域研究热点和难点。土壤斥水性是引发指流的一个重要因素。今后的研究中需进一步揭示土壤斥水性调控指流发生发展的物理机制，并构建和求解相应的数学模型，改进对指流中土壤水分含量时空分布的模拟精度。

针对斥水性土壤研究中存在的科学问题，有针对性的开展深入研究，有望进一步揭示土壤水分运动的微观物理机制，并在指流的理论模型及数值模拟方面取得突破，不仅对土壤物理学的理论基础本身，而且对其他相关学科如土壤水文学、农业生态学、土壤环境学和应用数学等具有重要的推动作用。

[1] Bayliss J S. Observations on Marasmius oreades and Clitocybegiganteaas parasitic fungi causing fairy rings[J]. Journal of Economic Biology, 1911, 6: 111－132.

[2] 杨邦杰，Blackwell P S，Nicholson d F. 土壤斥水性引起的土壤退化、调查方法与改良措施研究[J]. 环境科学，1993，15(4)：88－90.

Yang Bangjie, Blackwell P S, Nicholson D F. Soil degradation caused by soil water repellency, investigation methods and improvement measures[J]. Environmental Science, 1993, 15(4): 88－90. (in Chinese with English abstract)

[3] Voelkner A, Holthusen D, Ellerbror H, et al. Quantity of hydrophobic functional CH-groups-decisive for soil water repellency caused by digestate amendment[J]. International Agrophysics, 2015, 29: 247－255.

[4] Alanis N, Hernandez-Madrigal V M, Cerda A, et al. Spatial gradients of intensity and persistence of soil water repellency under different forest types in central Mexico[J]. Land Degradation and Development, 2017, 28(1): 317－327.

[5] Keesstra S, Wittenberg L, Maroulis J, et al. The influence of fire history, plant species and post-fire management on soil water repellency in a Mediterranean catchment: The Mount Carmel range, Israel[J]. Catena, 2017, 149: 857－866.

[6] Keck H, Felde V, Drahorad S, et al. Biological soil crusts cause subcritical water repellency in a sand dune ecosystem located along a rainfall gradient in the NW Negev desert, Israel[J]. Journal of Hydrology and Hydromechanics, 2016, 64(2): 133－140.

[7] Heydari M, Rostamy A, Najafi F, et al. Effect of fire severity on physical and biochemical soil properties in Zagros oak (Quercus brantii Lindl.) forests in Iran[J]. Journal of Forest Research, 2017, 28(1): 95－104.

[8] Tillman R W, Scotter D R, Wallis M G, et al. Water repellency and its measurement using intrinsic sorptivity[J]. Australian Journal of Soil Research , 1989, 27: 637－644.

[9] Doerr S H, Shakesby R A, Walsh R P D. Soil water repellency: Its causes, characteristics and hydro-geomorphological significance [J]. Earth-Science Reviews, 2000, 51: 33－65.

[10] Hallett P D, Lichner L, Kodesova R, et al. A brief overview of the causes, impacts and amelioration of soil water repellency-a review[J]. Soil and Water Research, 2008, 3: S21－S29.

[11] Cawson J G, Nyman P, Smith H G , et al. How soil temperatures during prescribed burning affect soil water repellency, infiltration and erosion[J]. Geoderma, 2016, 278: 12－22.

[12] Bughici T, WallachR. Formation of soil-water repellency in olive orchards and its influence on infiltration pattern[J]. Geodema, 2016, 262: 1－11.

[13] Rye C F, Smettem K R J. The effect of water repellent soil surface layers on preferential flow and bare soil evaporation[J]. Geoderma, 2017, 289: 142－149.

[14] 商艳玲，李毅，朱德兰. 再生水灌溉对土壤斥水性的影响[J]. 农业工程学报，2012，28(21)：89－97.

Shang Yanling, Li Yi, Zhu Delan. Effects of reclaimed water irrigation on soil water repellency[J]. Transactions of the Chinese Society of Agricultural Engineering, 2012，28(21)：89－97. ( in Chinese with English abstract)

[15] 杨昊天，刘立超，高艳红，等. 腾格里沙漠沙丘固定后土壤的斥水性特征研究[J]. 中国沙漠，2012，32(3)：675－682.

Yang Haotian, Liu Lichao, Gao Yanhong, et al. Characteristics of soil water repellency in fixed sand dunes in the Tengger Desert[J]. Journal of Desert Research, 2012, 32(3): 675－682. ( in Chinese with English abstract)

[16] 孙琪琪，刘前进，于兴修，等. 沂蒙山区桃园和玉米地棕壤斥水性空间分布及影响因素[J]. 陕西师范大学学报，2013，41：80－87.

Sun Qiqi, Liu Qianjin, Yu Xingxiu, et al. Spatial distribution and influencing factors of brown soil water repellency between peach orchard and corn field in Yimeng mountainous Area[J]. Journal of Shaanxi Normal University, 2013, 41: 80－87. (in Chinese with English abstract)

[17] 郭成久，陈乐，肖波，等. 黄土高原苔藓结皮斥水性及其对火烧时间的响应[J]. 沈阳农业大学学报，2016，47(2)：212－217.

Guo Chengjiu, Chen Le, Xiao Bo, et al. Soil water repellency of moss-dominated biological soil crust and their response to fire duration on the Loess Plateau of China[J]. Journal of Shenyang Agricultural University, 2016, 47(2): 212－217. (in Chinese with English abstract)

[18] Hallett P D, Bachmann J, Czachor H, et al. Hydrophobicity of soil[J]. Encyclopedia of Earth Sciences, 2011: 378－384.

[19] Wang Z, Wu L, Letey J. Indices for characterizing soil-water repellency and wettability[J]. Journal of Hydrology, 2000(231/232): 76－83.

[20] Bachmann J, Horton R, Ploeg R R, et al. Modified sessile drop method for assessing initial soil-water contact angle of sandy soil[J]. Soil Science Society of America Journal, 2000, 64(2): 564－567.

[21] Latey J, Osborn J, Pelishek R E. Measurement of liquid-solid contact angles in soil and sand[J]. Soil Science , 1962, 93: 149－153.

[22] Wang Q, GraberER, Wallach R.Synergisticeffects of geometry,inertia, and dynamic contact angle on wetting and dewetting of capillaries ofvarying cross section[J]. Journal of Colloid and Interface Science2013,396: 270－277.

[23] Czachor H, Doerr S H, Lichner L. Water retention of repellent and subcritical repellent soils: New insights from model and experimental investigations[J]. Journal of Hydrology, 2010, 380(1/2): 104－111.

[24] Shirtcliffe N J, Mchale G, Newton M I, et al. Critical conditions for the wetting of soils[J]. Applied Physics Letters, 2006, 89: 094101.

[25] Aminzadeh B, Dicarlo D A, Wallach R. The Effect of contact angle on saturation overshoot[J]. Vadose Zone Journal, 2011, 10: 466－468.

[26] Debano L F. The effect of hydrophobic substances on water movement in soil during infiltration[J]. Soil Science Society of America Journal, 1971, 35(2): 340－343.

[27] Wallis M G, Horne D J, McauliffE K W. A study of water repellency and its amelioration in a yellow brown sand:1. Severity of water repellency and the effects of wetting and abrasion[J]. New Zealand Journal of Agriculture Research , 1990, 33: 139－144.

[28] Hosseini M, Geissen V, Gonzalez-Pelayo O, et al. Effects of fire occurrence and recurrence on nitrogen and phosphorus losses by overland flow in maritime pine plantations in north-central Portugal[J]. Geoderma, 2017, 289: 97－106.

[29] Vogelmann E S, Reichert J M, Prevedello J, et al. Threshold water content beyond which hydrophobic soils become hydrophilic: The role of soil texture and organic matter content[J]. Geoderma, 2013, 209-210(11): 177－187.

[30] Ritsema C J, Dekker L W. Distribution flow: A general process in the top layer of water repellent soils[J]. Water Resources Research , 1995, 31: 1187－1200.

[31] Burch G J, Moore I D, Burns J. Soil hydrophobic effects on infiltration and catchment runoff[J]. Hydrological Processes, 1989, 3: 211－222.

[32] Ritsema C J, Dekker L W, Hendrickx J M H, et al. Preferential flow mechanism in a water repellent sandy soil[J]. Water Resources Research ,1993, 29: 2183－2193.

[33] Ritsema C J, Dekker L W. Distribution flow: A general process in the top layer of water repellent soils[J]. Water Resources Research , 1995, 31: 1187－1200.

[34] Wallach R,JortzickC. Unstable finger-like flow in water-repellent soils duringwetting and drainage-the case of a point water source[J]. Journal of Hydrology, 2008, 351: 26－41.

[35] Wallach R. The effect of soil water repellency on moisture distribution from asub-surface point source[J]. Water Resources Research,2010,46(8):863.

[36] Wallach R, Margolis M, Graber E R. The role of contact angle on unstable flow formation during infiltration and drainage in wettable porous media[J].Water Resources Research, 2013, 49(10): 6508－6521.

[37] Annaka T, Hanayama S. Effects of contact angle on fingered flow during non-ponding infiltration into dry sand layers[J]. Soil Science and Plant Nutrition,2010, 56: 366－370.

[38] Bachmann J, Horton R, Ploeg R R. Isothermal and nonisothermal evaporation from four sandy soils of different water repellency[J]. Soil Science Society of America Journal, 2001, 65: 1599－1607.

[39] 李毅，任鑫. 覆膜开孔条件下斥水性层状土壤蒸发实验[J].农业机械学报，2012，43(1)：68－75.

Li Yi, Ren Xin. Evaporation experiments on layered water-repellency soil under perforated plastic mulch[J]. Transactions of the Chinese Society for Agricultural Machinery, 2012, 43(1): 68－75. (in Chinese with English abstract)

[40] Gupta B, Shah D O, Mishra B, et al. Effect of top soil wettability on water evaporation and plant growth[J]. Journal of Colloid and Interface Science, 2015, 449: 506－513.

[41] Bauters T W J, Steenhuis T S, Dicarlo D A, et al. Physics of water repellent soils[J]. Journal of Hydrology, 2000(231/232): 233－243.

[42] Jury W A, Gardner W R, Gardner W H. Soil Physics[M], Wiley, New York, 1991.

[43] Dicarlo D A, Bauters T W J, Darnault C J G, et al. Lateral expansion of preferential flow paths in sands[J]. Water Resources Research, 1999, 35: 427－434.

[44] Diamantopoulos E, Durner W, Reszkowska A, et al, Effect of soil water repellency on soil hydraulic properties estimated under dynamic conditions[J]. Journal of Hydrology, 2013, 486: 175－186.

[45] Dicarlo D A. Stability of gravity-driven multiphase flow in porous media: 40 years of advancements[J]. Water Resources Research, 2013, 49: 4531－4544.

[46] Hilfer R, Steinle R. Saturation overshoot and hysteresis for

two phase flow in porous media[J]. European Physics Journal Special Topics, 2014, 223 (11):2323－2338.

[47] Xiong Y. Flow of water in porous media with saturation overshoot: A review[J]. Journal of Hydrology, 2014, 510: 53－362.

[48] Dicarlo D A. Experimental measurements of saturation overshoot on infiltration [J].Water Resources Research, 2004, 40: W04215.

[49] Geiger S L, Durnford D S. Infiltration in homogeneous sands and a mechanistic model of unstable flow[J].Soil Science Society of America Journal, 2000, 64(2): 460－469.

[50] Furst T, Vodak R, Sir M, et al. On the incompatibility of Richards’ equation and finger-like infiltration in unsaturated homogeneous porous media[J]. Water Resources Research, 2012, 45: W03408.

[51] Eliassi M, Glass R J. On the porous-continuum modeling of gravity-driven fingers in unsaturated materials: Extension of standard theory with a hold-back-pile-up effect[J]. Water Resources Research, 2002, 38(11): 1234.

[52] HilperT M. Velocity-dependent capillary pressure in theory for variably-saturated liquid infiltration into porous media[J]. Geophysics Research Letters, 2012, 39: L06402.

[53] Baver C E, Parlange J Y , Stoof C R, et al. Capillary pressure overshoot for unstable wetting fronts is explained by Hoffman’s velocity-dependent contact-angle relationship[J]. Water Resources Research, 2014, 50: 5290－5297.

[54] Doster F, Hilfer R. A comparison between simulation and experiment for hysteretic phenomena during two-phase immiscible displacement[J]. Water Resources Research, 2014, 50: 681－686.

[55] Hoenig O, Zegeling P A , Doster F, et al. Non-monotonic travelling wave fronts in a system of fractional flow equations from porous media[J]. Transport Porous Media, 2016, 114: 309－340.

[56] Cueto-Felgueroso L, Juanes R. Nonlocal interface dynamics and pattern formation in gravity-driven unsaturated flow through porous media[J]. Physical Review Letters, 2008, 101(24): 244504.

[57] Dicarlo D A, Aminzadeh B, Dehghanpour H. Semicontinuum model of saturation overshoot and gravity-driven fingering in porous media[J]. Water Resources Research, 2011, 47: W03201.

[58] Joekar-Niasar V, Hassanizadeh S, Dahle H. Non-equilibrium effects in capillarity and interfacial area in two-phase flow: Dynamic pore-network modeling[J]. Journal of Fluid Mechanics, 2010, 655: 38－71.

[59] Xiong Y, Furman A, Wallach R. Moment analysis description of wetting and redistribution plumes in wettable and water-repellent soils[J]. Journal of Hydrology, 2012(422/423): 30－42.

[60] Xiong Y, Wallach R, Furman A. Modeling multidimensional flow in wettable and water-repellent soils using artificial neural networks[J]. Journal of Hydrology, 2011, 410: 92－104.

[61] 杨邦杰，Blackwell P S，Nicholson D F. 斥水土壤中的水热运动规律与数值模型[J]. 土壤学报，1996，33(4)：351－359.

Yang Bangjie, Blackwell P S, Nicholson D F. Modeling water and heat movement in a water-repellent sandy soil[J]. Acta Pedologica Sinica, 1996, 33(4): 351－359. (in Chinese with English abstract)

[62] 李毅，商艳玲，李振华，等. 土壤斥水性研究进展[J]. 农业机械学报，2012，43(1)：68－75.

Li Yi, Shang Yanling, Li Zhenhua, et al. Advance of study on soil water repellency[J]. Transactions of the Chinese Society for Agricultural Machinery, 2012, 43(1): 68－75. (in Chinese with English abstract)

[63] Chapuis O, Prat M. Influence of wettability conditions on slow evaporation in two-dimensional porous media[J]. Physical Review E, 2007, 75: 046311.

[64] Lehman N P, Assouline S, Or D. Characteristic lengths affecting evaporative drying of porous media[J]. Physical Review E, 2008, 77: 056309.

[65] Shokri N, Lehman P, Vontobel P, et al. Characteristics of evaporation from partially wettable porous media[J]. Water Resources Research, 2009, 45: W02415.

[66] Shokri N, Lehman P, Vontobel P, et al. Drying front and water content dynamics during evaporation from sand delineated by neutron radiography[J]. Water Resources Research, 2008, 44: W06418.

[67] Kim D H, Yang H J, Kim K Y, et al. Experimental investigation of evaporation and drainage in wettable and water-repellent sands[J]. Sustainability, 2015, 7(5): 5648－5663.

[68] Nisson A, WanG Q, Wallach R. Kinetics of gravity-driven slug flow in partially wettable capillaries of varying cross section[J]. Water Resources Research, 2016, 52: 8472－8486.

[69] Schluter S, Berg S, Rucker M, et al. Pore-scale displacement mechanisms as a source of hysteresis for two-phase flow in porous media[J]. Water Resources Research, 2016, 52: 2194－2205.

[70] Brindt N, Wallach R. The moving-boundary approach for modeling gravity-driven stable and unstable flow in soils[J]. Water Resources Research, 2017, 53: 344－360.

Review on soil water movement affected by soil water repellency

Wang Qiuling1, Shi Fanxin1, Liu Zhipeng2※, Xiong Yunwu3

(1.,,236037,; 2.,,210095,; 3.,,100083,)

Soilwater repellency (SWR) is a normal property with major repercussions for plant growth, surface and subsurface hydrology, and for soil erosion. Important advances have been made since the late 1960s in identifying the range of environments affected by SWR, its characteristics and its hydro-geomorphological impacts. In this review, we outlined the concept of SWR, summarized the commonly used methods of soil water content (SWC) measurement and classification criterion, but focused particularly on recent advances in identifying the impacts of SWR on water movements, and indicated the existing research gaps. Significant advances relating to the impacts of SWR on the hydraulic properties as well as the dynamics of water infiltration and evaporation in these unique systems were discussed. SWR affected the matric potential through the contact angle, and shifts the water entry values. The wetting branch of water retention curves is strongly affected by the contact angle, in contrast, effects for the drying branch are minimal, SWR can resist or retard surface water infiltration. Besides the retardation or resistance of surface water infiltration, water repellent soils have been associated with fingered flow. Fingers are known to have a distinctive nonmonotonic saturation profile, with water accumulation behind the wetting front (tip) and lower saturation above it (tail). This nonmonotonic saturation profile is known as saturation overshoot. Saturation overshoot is associated with capillary pressure overshoot and has been confirmed to be the cause for gravity driven fingering. However, the saturation overshoot cannot be described by the Richards equation, the primary unsaturated flow equation. Richards’ equation in its basic form, along with the standard (monotonic) pressure-saturation relations is incompatible with the saturation overshoot for fingered flow. Modifications of Richards’ equation and other approaches have been proposed to account for and describe the nonmonotonicity of the saturation field. In comparison with numerous work on infiltration, studies on evaporation are relatively less but show uniform results, namely SWR suppresses soil evaporation. Percolation-based morphological pore network modeling of evaporation confirms the results. Experimental and modeling results suggest that water repellency affects liquid phase continuity in partially wettable porous media and reduces the evaporation characteristic length relative to capillarity effects. Major research gaps, however, remain in (a) identifying the exact role of, and the interactions between the variables controlling the development and effectiveness of flow pathways through repellent soils; (b) establishing and improving the models with new mechanisms with consideration of the effects of SWR in controlling fingers, and proposing the relevant analytical and numerical methods for solving these new models. Improved understanding of effects of SWR will enable its overall roles in surface and subsurface hydrological and erosion processes to become more clearly defined.

soils; moisture; evaporation; water repellency; soil hydraulic properties; finger flow

10.11975/j.issn.1002-6819.2017.24.013

S152.7

A

1002-6819(2017)-24-0096-08

2017-08-28

2017-12-05

国家自然科学基金项目（41701254,41771258），安徽省国际科技合作项目（1403062027），阜阳市政府-阜阳师范学院横向合作项目（XDHX2016008）

王秋玲，女（汉族），广东梅州人，副教授，博士，主要从事土壤水分运移研究。Email：qiulingwangql@163.com

刘志鹏，男（汉族），讲师，博士，主要从事土壤水分运移、土壤性质空间变异等方面研究。Email：zpliu0306@126.com

王秋玲，施凡欣，刘志鹏，熊云武. 土壤斥水性影响土壤水分运动研究进展[J]. 农业工程学报，2017，33(24)：96－103. doi：10.11975/j.issn.1002-6819.2017.24.013 http://www.tcsae.org

Wang Qiuling, Shi Fanxin, Liu Zhipeng, Xiong Yunwu. Review on soil water movement affected by soil water repellency[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2017, 33(24): 96－103. (in Chinese with English abstract) doi：10.11975/j.issn.1002-6819.2017.24.013 http://www.tcsae.org