基于LH-OAT的推理公式法参数敏感性分析

孙 毅

(中水北方勘测设计研究有限责任公司，天津300222)

基于LH-OAT的推理公式法参数敏感性分析

孙 毅

(中水北方勘测设计研究有限责任公司，天津300222)

为定性了解不同洪水频率下汇流参数m，平均比降J两个参数对推理公式法进行无资料地区产流模拟的影响，利用LH-OAT全局敏感度分析方法对推理公式法进行参数敏感性分析。以两个不同分区的小流域(山西省方山县圪洞沟和孝义市下堡河流域)汇流为例，研究确定不同洪水频率下推理公式法参数的敏感性，确定参数敏感程度和变化规律，为模型参数率定提供数值参考。研究表明，推理公式法参数对洪峰值敏感性排序为m>J；m和J的敏感性随着洪水频率的减小呈现减弱趋势，两个参数随洪水频率变化的速率为Vm>VJ。

敏感性分析；洪水频率；推理公式法；LH-OAT模型

0 概 述

1 推理公式法

从1956年开始，中国水利水电科学研究院就研究小流域暴雨洪水计算方法，于1958年提出了推理公式，现行《水利水电工程洪水计算规范》中有关小流域设计洪水就是利用该院推理公式计算的。推理公式法是从暴雨形成洪水的成因出发。即由暴雨推求流域设计洪峰流量，属于成因推理方法，是半理论半经验公式，是无资料小流域计算洪水的主要方法。公式分为部分产流和全面产流两部分。即

tc>τ时，为全面产流情况，则

(1)

tc≤τ时，为部分产流情况，则

(2)

式中，A为计算单元面积，km2；L为主河道长度，km；J为主河道比降， ‰；m为汇流参数，Sp为设计雨力，mm/h;τ为汇流时间，h；tc为产流历时，h；n为暴雨衰减系数；μ为平均入渗率，mm/h。

2 公式中各参数不确定性的初步分析

从式(1)、式(2)可知，只要知道参数A、L、J、n、μ、m、Sp便可求出推理公式的洪峰。现分别对上述7个参数进行不确定性分析。其中，A与L通过高精度的DEM数据提取可以较准确提取，具有很强的确定性，误差很小。n与μ一般采取当地水文手册提供数据，确定性也较强。Sp=H24/241-n，24 h地区平均降雨量由其多年平均值推求，根据《山西省水文手册》中数据进行计算，精度较高，可靠性强。J由分段加权来确定，分段点和分段距离因人而异会有很大不同，造成了J的不确定性。不同地类m各不相同，m=∑cimi(ci表示各地类的权重系数)，m范围较广，取值具有很强的不确定性。

3 LH-OAT全局敏感性分析方法

LH-OAT是水文模型中参数定性全局敏感度的分析方法，由拉丁超立方抽样(Latin-Hypercube)和随机OAT方法组成[3- 4]。LH-OAT方法的原理是通过微小改变水文模型参数来观察目标函数数值的变化程度，最终通过一个无量纲数来表示该参数对目标函数的敏感度[4]。假设水文计算模型有P个参数，运用LH-OAT方法对其进行全局敏感性分析，具体计算步骤如下：第一，将每个参数在其取值区间均等分成n层，要求每个参数的分层数相同；第二，运用拉丁超立方抽样法在每个分层上抽取一个采样点，共抽取n个采样点；第三，将采样点参数值带入目标函数进行计算，然后分别对P个参数进行微小变化并计算，每次计算只改变一个参数值，改变方向随机。对于n个分层P个参数，LH-OAT模型共进行了n×(P+1)次运算。每个参数的相对敏感度由公式(3)计算得到

Si，j=200×

(3)

式中，j为拉丁超立方抽样采样点标识j∈[1，n]；αi为参数ei极小变化程度，eiαi值一般占区间的5%～10%；Si，j为参数ei在j采样点的相对敏感度，Mj为j采样点对应的目标函数。参数ei的最终敏感性指标Si为各采样点ei的相对敏感度平均值

(4)

4 模型敏感性分析

4.1 小流域概况

流域1——山西方山县圪洞沟流域属于黄河支流北川河流域，位于山西省西北部山区、省水文西区，属大陆性季风气候。流域2——山西孝义市下堡河流域属于黄河支流汾河流域，位于山西省中部平原区、省水文中区，属于温带大陆性气候。两小流域内没有水文站及相关水文资料，属于无资料地区，用推理公式法对其进行5、10、20、50、100年设计洪水计算。两流域面积及其各汇流地类面积见表1。

4.2 参数范围确定

在圪洞沟与下堡河两个小流域对推理公式法各参数进行敏感性分析，分析参数主要为m和J。根据m=∑cimi，考虑圪洞沟下垫面情况，在表2中选取上下限值，得出m的取值范围为0.147～0.241。针对圪洞沟的具体情况，通过不同分段点的划分，确定J的取值范围为26.5‰～34‰。考虑下堡河下垫面情况和河道比降不同的划分，在表3中选取上下限值，得出m的取值范围为0.122～0.263，确定J的取值范围为21.5‰～30.5‰。

表1 流域内各汇流地类面积及河长

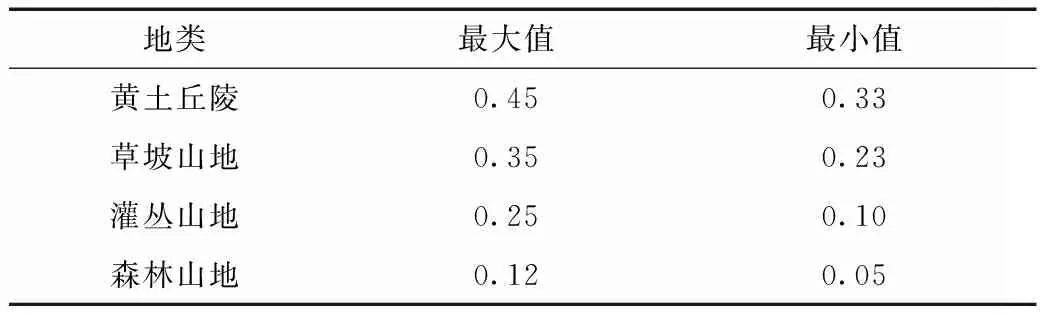
表2 流域各汇流地类参数取值范围[5]

表3 两流域参数敏感性指标数值

4.3 模型参数敏感性计算

利用LH-OAT对双曲正切模型产流计算进行敏感性分析：首先，将推理公式法的参数m、J均分成3份及4层，1%、2%、5%、10%和20%设计洪水频率，共确定5个独立计算模块；然后，利用拉丁超立方抽样法进行取样组合，每种洪水频率确定4种组合，共确定20种不同组合；最后按照OAT分析计算方法，利用式(1)对每种组合和组合每个参数微小变化(保持1个参数不变，对剩余一个参数进行微小变化，本次变化值为10%)后数据进行计算，每种组合计算3次，每种洪水频率计算12次，5种频率共计算60次；利用式(2)对每种降雨频率的计算结果进行均值处理，最终得到5组反映不同降雨频率的两个参数m、J敏感性的无量纲数值(见表3)。同降雨频率下三个参数敏感性程度和参数在不同降雨频率在敏感程度变化规律见图1与图2。

图1 圪洞沟流域不同洪水频率参数敏感指标

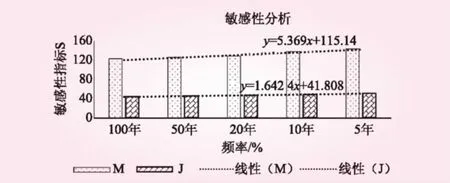
图2 下堡河流域不同洪水频率参数敏感指标

4.4 敏感性结果分析

通过表3和图1、图2可以得出如下结论：

(1)同洪水频率情况下，推理汇流模型两个参数中汇流参数m最为敏感，且随着洪水频率的变化，推理汇流模型两个参数的敏感性程度排序不会发生变化，始终为m>J。

(2)推理汇流模型的m、J敏感性随着洪水频率的减小呈现减弱趋势，洪水频率越小参数对推理汇流模型洪峰结果影响越小。

(3)由图1与图2不同洪水频率下推理汇流模型的两个参数线性趋势线方程可以看出，m的敏感性随着洪水频率减小，其减弱速度加快；J的敏感性随着洪水频率的减小，其减弱速度比m减弱速率小，推理汇流模型两个参数的敏感性随降雨频率减小变化速率为Vm>VJ。

(4)因为圪洞沟小流域属于山西西部山区，山西水文西区；下堡河流域属于山西中部平原区，山西水文中区；两个流域的主雨型都不相同，通过对比图1与图2可以看出两个不同分区的小流域汇流参数m与J的敏感性变化趋势一致，规律相同。

5 结 论

推理汇流模型模型中参数m十分敏感，参数J较为敏感，两者皆随降洪水频率成线性变化。不同地区两个参数敏感性变化趋势一致，规律相同，具有一定的推广性，有借鉴意义。在实际工程中，用推理汇流模型计算无资料地区小流域洪峰时，由于小流域一般计算的设计洪水频率较大，m与J敏感性变大，微小的变化对结果影响很大；所以，应仔细研究流域情况，有针对性地调整参数m和J，以期反映无资料小流域地区最真实产汇流情况，从而提高模型可靠性。

[1] 叶守泽, 詹道江. 工程水文学[M]. 北京： 中国水利水电出版社, 2005: 264- 265．

[2] 晁锐, 郭建清, 冯晓旭. 推理公式法计算参数的不确定性和灵敏性[J]. 人民珠江, 2015(4)： 29- 31．

[3] GRIENSVEN A, MEIXNERT, GRUNWALD S, et al. A global sensitivity analysis tool for the parameters of multi-variable catchment models[J]. Journal of Hydrology, 2006, 324(1- 4): 10- 23．

[4] 徐会军, 陈洋波, 李昼阳, 等. 基于LH-OAT分布式水文模型参数敏感性分析[J]. 人民长江, 2012, 43(7)： 19- 23．

[5] 山西省水利厅. 山西省水文计算手册[M]. 郑州： 黄河水利出版社, 2011．

ParameterSensitivityAnalysisofReasoningFormulaMethodBasedonLH-OATSensitivityAnalysis

SUN Yi

(China Water Beifang Investigation, Design & Research Co., Ltd., Tianjin 300222, China)

In order to analyze the influences of confluence parametermand average gradientJat different flood frequency on runoff simulation in regions without data, the LH-OAT sensitivity analysis is used to analyze the parameter sensitivity of reasoning formula method. Taking two different small basins in Gedong Ditch, Fangshan County, Shanxi Province and Xiabao River, Xiaoyi County, Shanxi Province as examples, the parameter sensitivity of reasoning formula method at different flood frequency are analyzed and the level of parameter sensitivity and change rule are determined to offer numerical reference for parameter rating of model. The analysis shows that the rank order of parameter sensitivity to flood peak value in reasoning formula method ism>J, the sensitivities ofmandJhave a weak trend with the reduction of flood frequency, and the velocity change of two parameters with flood frequency isVm>VJ．

sensitivity analysis; flood frequency; reasoning formula method; LH-OAT sensitivity analysis

TV214

A

0559- 9342(2017)09- 0023- 03

2016- 12- 01

山西省国际科技合作计划项目(2013081034)；山西省水利厅水利技术项目研究与推广项目；2015年度山西省研究生教育创新项目(2015SY18)

孙毅(1990—)，男，山西吕梁人，硕士，研究方向为水文及水资源．

(责任编辑陈 萍)