基于有限元极限平衡法的锚固边坡稳定性分析

种记鑫

（济南轨道交通集团有限公司，山东 济南 250101）

基于有限元极限平衡法的锚固边坡稳定性分析

种记鑫

（济南轨道交通集团有限公司，山东 济南 250101）

在平面应变条件下，采用极限平衡和有限元法对锚固边坡稳定性评价过程的关键问题进行研究。将条分法对锚固边坡安全系数的定义推广到有限元法中，通过弹塑性有限元分析计算结构整体应力场，再结合虎克-捷夫法完成最危险滑动面的优化搜索。以天然边坡、渗流作用下锚固边坡及开挖锚固边坡为例，对比分析了条分法、有限元极限平衡法及有限元强度折减法三者在安全系数大小、滑动面形状、位置及对锚固作用处理上的差异。结合工程实例分析发现：同条分法相比，有限元方法所得到的安全系数更大，滑动面也更深，其中，有限元极限平衡法具有良好的计算精度，而条分法在一定程度上削弱了锚固效应，有限元强度折减法在一定程度上会放大了锚固结构的稳定效果。

锚固边坡；有限元极限平衡法；有限元强度折减法；稳定性

P315.69；TU 457

A

10.13693/j.cnki.cn21-1573.2017.04.006

1674-8565（2017）04-0032-07

2017-06-12

2017-09-15

种记鑫（1984-），男，山东省聊城市人，2006年毕业于山东理工大学，本科，工程师，现主要从事基坑工程技术、隧道工程技术、地图建设管理方面的工作。

0 引言

边坡安全性问题一直是土木、水利学科中的重点研究课题，针对一般边坡问题，最有效且最经济的加固措施是采用锚杆加固。锚杆加固边坡自身参数决定了其安全性的本身数值，但计算模型及理论方法决定了安全系数的范围。在边坡锚固设计时需要对锚固后边坡稳定性改善情况进行准确评价，通过理论分析寻找真实的安全系数。在传统边坡计算方法中，条分法[1-2]概念清晰，物理意义明确，实践经验丰富，但局限性同样明显：由于将潜在滑动土体视为刚体，其锚固作用仅体现在结构抗剪力对力或力矩平衡上，实际潜在滑动土体受应力二次分配影响，更加无法反映地层与锚固结构共同加固的效果。

有限元强度折减法自动满足平衡条件及相容性条件，较条分法的理论体系更加严格，且无需假定滑动面的形状和位置。因此，自1975年Zienkiewicz等人提出之后受到广泛关注，随后Matsui与San从理论与数值计算两方面证明了采用有限元强度折减法进行边坡稳定性分析的合理性。郑颖人等[3]采用有限元强度折减法对预应力构锚索作用下的边坡安全系数进行了探究，但仅对土体参数采取了变换，并没有对锚索参数是否同时换算进行研究；韦立德等[4-5]在前人研究的基础上，考虑了在对锚杆强度进行折减的同时锚杆持力层也进行强度折减；施建勇等[6]在折减地层参数的前提下，提出切向弹性模量的折减算法，并将潜在滑动区域能量积分面积与换算参数关系交点所得到的相关系数定义为边坡参考系数；白冰等[7]将经典强度折减法纳入双折减法的计算过程，并从理论与数值模拟两方面证明了双折减法几乎总是小于经典强度折减法；Isakov和Moryachkov[8]通过建立了综合安全系数和强度折减路径之间的关系，提出了基于最短应力路径原则的最小综合安全系数计算公式；薛海滨等[9]基于土体材料强度参数线性衰减假定，将内聚力折减系数与内摩擦角折减系数之间的非等比例相关关系引入传统的有限元强度折减法中，提出（以）抗剪强度参数对抗滑力的贡献为权重的综合安全系数。但这些研究对于非均质边坡的不同土层是否采用同一折减系数和带有加固结构的边坡加固结构的强度是否折减等问题没有进行深入的研究与讨论。

有限元极限平衡有机结合了条分法与有限元法的优点，又能够避免使用强度折减法而引起诸多争议，近年来在各类边坡安全性分析及土工构件性能相关参数的研究中被大量应用[10-12]，并取得了良好的工程效果。本文利用有限元极限平衡法直接评价锚固边坡的稳定性，并对其中的一些关键问题进行了探索，所得规律可为相关研究提供借鉴与参考。

1 锚固边坡稳定分析方法

1.1 极限平衡条分法

极限平衡法的缺点：极限平衡条分法假定土体是散性刚体，联合静力平衡原理及摩尔库伦准则共同推导边坡的抗滑系数。两种理论均是在宏观角度上判断土体状态，未考虑土体单元应力状态对边坡稳定性的贡献值，无法根据土体应力应变等微观状态上推算边坡的危险位置。极限平衡法的优点：极限平衡条分法假设条件中，很大程度上减少了未知参数的数目，其安全系数依据瑞典圆弧法计算，如图1所示。锚固结构对抗滑力（力矩）的贡献可表示为单变量的离散函数式：

式中，Tk为第k排锚杆锚固段最大抗力，Shk为第k排锚杆水平间距，βi为第k根锚固体与圆弧切线夹角，ϕi为土条i的内摩擦角。则考虑支护结构作用的边坡整体稳定安全参数FS计算方法为：

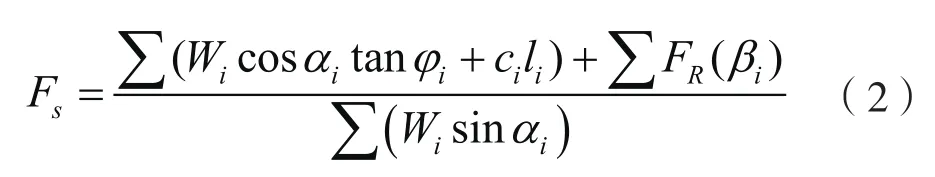
式中，Wi为土条i的自重和地面荷载，li为滑动面的长度；iα为第i土条圆弧破坏面切线与水平面的夹角，ci为土条i的内聚力。

图1 土质锚固边坡条分计算模型Fig.1 Stability analysis for anchored soil slope using slice method

1.2 有限元强度折减法

在使用强度折减法分析锚固边坡稳定时，采取稳定性系数FS通过式（3）对地层的抗剪强度参数C和φ换算折减，并根据非关联流动准则，采用经典弹塑性破坏模型和摩尔库伦屈服准则，反复迭代，当数值迭代计算一直无法趋于某一稳定值时，可判断结构发生失稳破坏。

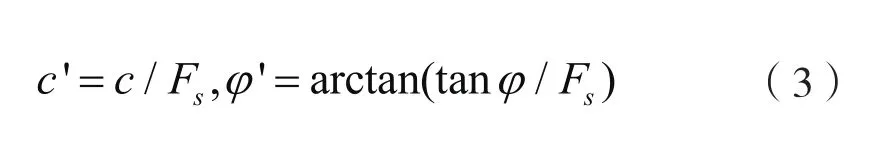
有限元轻强度折减法在工程应用中存在缺陷：边坡土体未发生塑性破坏之前，内粘聚力、内摩擦角与重力、边坡自身尺寸参数有关，但在土体出现塑性区之后，内粘聚力和内摩擦角与滑裂面的正应力、剪应力密切相关，且在sinϕ≥1−2ν塑性区会出现失真。有限元强度折减法的优点：有限元强度折减法通过不断降低岩土体强度使边坡达到极限破坏状态，从而可以直接计算得到边坡的破坏滑动面和强度储备安全系数，十分贴近工程设计。

1.3 有限元极限平衡法

边坡破坏具有联动效应，微小单元的塑性破坏会迅速扩展到临近单元，引发大面积土体失稳。某范围土体应力应变状态根据判断准侧达到极限值时，即可判断边坡发生失稳破坏。该方法的优点：有限元极限平衡法通过探寻程序搜索假设滑裂面上的应力应变值，按照公式（4）计算各滑裂面的安全系数。该方法无需假定土条间的相互作用力状态，且不存在应力反复迭代和不收敛的情况，计算简单方便。

1.3.1 安全系数定义

借鉴条分法对锚固边坡稳定性分析的思路，并结合有限元应力分析，锚固边坡整体稳定性系数FS可定义为：

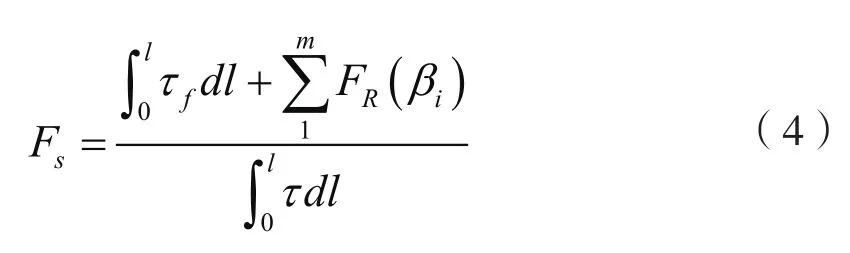
式中，fτ为滑动面的安全抗剪强度，τ为滑动面剪应力值。

1.3.2 最危险滑动面搜索

边坡有限元安全计算可看作是带有限制边界的广义数学计算。其具体的计算流程可用文字描述为：在给定的应力场中，对一水平坐标值确定的点，根据相应条件求解该点竖向坐标，并结合下一点的双向坐标，根据某一关系使一系列点的连线组成的曲线得到的Fs值最小，该曲线即最危险滑裂面。其计算程序如图2所示。

图2 极易发生滑动面探寻程序Fig.2 Searching flow chart of the most dangerous sliding surface

但极限平衡法没有考虑应力应变关系，难以给出一定受力条件下的边坡受力关系，且在分析对应于边坡处于极限受力平衡状态时，所得的土条间内力或土条底部的反力与实际工作条件下对应的物理量存在区别。

2 锚固边坡有限元稳定性分析

2.1 普通边坡稳定结果对比分析

该边坡为土质边坡，周边无超载，无孔隙水。坡高为10m，坡高比值为1:2，为降低模型边界条件效应对计算结果的影响，坡脚及坡顶各横向延伸20m。模型边界条件为：坡体底部为固定铰支座，四周边界为水平链杆约束，顶部为自由面。地层体材料力学参数如表1所示。

表1 地层体材料力学参数

依据设计相关要求，自坡面下1m处起，按水平角15o，竖向间距2m，水平间距1m，布设5排总长20m、锚固段长5m、直径0.1m的锚杆。锚固段注浆采用M30水泥砂浆，注浆体抗剪强度约47kPa。

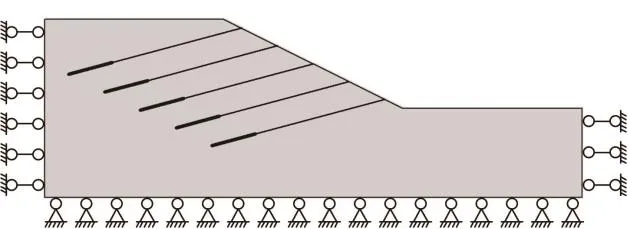
图3 锚杆及约束条件模型Fig.3 Schematic diagram of anchorage and constraint condition

2.1.1 天然边坡稳定性分析

首先取不考虑锚固结构作用的天然边坡作为分析对象，分别根据极限平衡条分法、有限元极限平衡法及有限元强度折减法进行安全性计算，安全系数值见表2。从表中可以看出，这几种方法所得安全系数高度相似，极限差值仅为1.6%，其中毕肖普法假定各土条底部滑动面上的抗滑系数均相同，忽略了底部土体的自稳性，得出的结果相对较低。

表2 无锚固结构的安全系数

图4给出了极限平衡条分法、有限元极限平衡法的滑动面及采用剪应变增量表征的有限元强度折减法所得滑动面。图中橘黄色条纹代表剪应变增量表征的有限元强度折减法所得滑动面，可以看出，三个滑动面的滑入、滑出位置以及滑动面的形状基本一致，两类有限元方法所得滑动面较极限平衡条分法略深。

图4 天然边坡滑动面位置Fig.4 Sliding surface of natural slope

2.1.2 锚固边坡稳定性分析

针对上述天然边坡进行锚固处理，采用极限平衡条分法、有限元极限平衡法及有限元强度折减法计算得到的安全系数见表3。从表中可以看出，有限元强度折减法所得安全系数较毕肖普法增大约6.38%，有限元极限平衡法较毕肖普法增大约4.25%。

表3 考虑锚固结构的安全系数

如图5所示，锚固后两类有限元方法所得的滑动面位置同毕肖普法相比，明显向土体深处移动，而有限元强度折减法所得滑弧的终止位置略微向坡脚处移动。

图5 锚固边坡滑动面位置Fig.5 Sliding surface of anchored soil slope

2.2 渗流作用下锚固边坡稳定结果对比分析

某回填土质边坡分两级填筑，自下往上坡高比分别为1: 0.8和1: 0.75，由于渗流作用导致结构稳定性下降，从而需要进行加固处理。土地层力学参数如表4所示。

表4 地层力学参数

自坡面下6m处起，按水平角30o，竖向间距6m，水平间距1m，布设2排锚固段直径0.3m、非锚固段截面积0.00109m2的锚杆。第一排锚杆总长为18m，其中锚固段长6m。第二排锚杆总长为15m，锚固段长5m，结构尺寸及锚固情况如图6所示。

图6 边坡剖面计算简图Fig.6 Computational profile of slope

2.2.1 渗流作用下无锚固边坡稳定性分析

考虑渗流场影响后，锚固前边坡安全系数值如表5所示。有限元法给出的安全系数略大于毕肖普法，但最大相差仅4.3%，所得滑弧的起始与终止位置同毕肖普法基本一致（图7）。

表5 渗流作用下无锚固结构的安全系数

图7 渗流作用下无锚固结构边坡滑动面位置Fig.7 Sliding surface without anchoring under seepage

2.2.2 渗流作用下锚固边坡稳定性分析

采用锚杆支护后土体安全系数如表6所示，从中可以看出，两种有限元方法计算得到的安全系数值虽均高于条分法，但相差不大，同锚固前基本一致，最大相差值仅为4.36%。

表6 渗流作用下有锚固结构的安全系数

但与之对应的最危险滑动面则相差较大，如图8所示，同毕肖普法相比，有限元法所得滑弧更深；相对于算例4.1，有限元强度折减法所得滑弧的终止位置向坡脚处移动更加明显。

图8 渗流作用下锚固边坡滑动面位置Fig.8 Sliding surface with anchoring under seepage

2.3 开挖边坡稳定结果对比分析

选用开挖深度为4m的建筑边坡为算例，对本文方法进行深入分析验证。算例开挖面坡高比为1:0.3，分两次进行开挖，每次开挖2m，具体开挖过程如图9所示。边坡土体分上下两层，其物理力学参数见表7。

图9 边坡几何形状及开挖过程Fig.9 Geometric model of slope and excavation process

表7 土体材料力学参数

2.3.1 无支护边坡开挖稳定性分析

该基坑开挖完成后的安全系数值汇总于表8。其中有限元极限平衡法及有限元强度折减法考虑两步开挖。极限平衡条分法无法考虑开挖影响。有限元法安全系数的计算依赖于单元应力场，而随着坡度的增大，坡脚处容易产生应力集中现象，对计算精度造成一定影响。从安全指数的分析数值中也可以看出，三种方法得出的安全系数差别略大。同毕肖普法结果相比，有限元极限平衡法增大约5.7%，有限元强度折减法增大约8.9%。

表8 无支护边坡开挖的安全系数

由图10可以看出，两类有限元方法的结果吻合较好，极限平衡条分法所得滑动面的滑入位置相对更加靠近开挖面，滑出位置及滑面形状与有限元方法结果高度吻合。

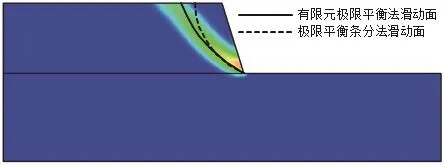
图10 无支护边坡开挖滑动面位置Fig.10 Sliding surface of excavation slope without anchoring

2.3.2 锚固支护边坡开挖稳定分析

在开挖过程中使用一排锚杆进行支护，杆体注浆强度等级为M30的水泥砂浆。锚固段长4m，直径0.4m，自由段长5m，纵向间距1.0m，距地表竖直距离为1.0m，倾角15o。第一步开挖后打孔，打入锚杆，注入水泥砂浆并假设锚杆立即受力，在施工时间间隔不长的情况下，这种假设对计算结果的影响可以忽略不计。

表9列出了锚杆支护后三种方法的安全系数计算结果，从中可以看出，两种有限元方法计算得到的安全系数值均高于条分法；同未支护开挖基坑一样，不同方法所得安全系数之间的差距也进一步增大，同毕肖普法结果相比，有限元极限平衡法增大约12.07%，有限元强度折减法增大约14.41%。

表9 支护作用下边坡开挖的安全数值

如图11所示，三个最危险滑动面位于坡后位置的部分基本一致，而由于应力释放、坑底隆起等原因，位于坡脚附近的部分则差别较大。两类有限元法所得滑动面向土体深处移动，而同算例相比，随着坡度的增大，有限元强度折减法所得滑弧的终止位置向坡脚处移动愈加明显。

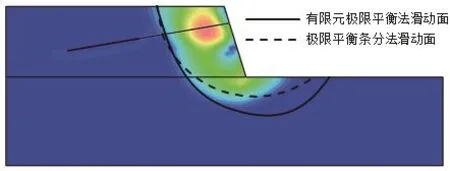
图11 支护边坡开挖滑动面位置Fig.11 Sliding surface of excavation slope with anchoring

2.4 条分法与有限元法锚固效应的差异分析

极限平衡法、有限元极限平衡法和有限元强度折减法在锚固边坡进行稳定性评价时考虑锚固结构的作用，但三者对锚固作用的处理存在着本质区别。

锚固力在极限平衡法和有限元极限平衡法计算安全系数时，均被当作集中荷载力来处理。但不同的是，在极限平衡法中锚固结构的作用局限于式（4）中项；而在有限元极限平衡法中，锚固结构参与了有限元应力场的计算，改变了土体的应力分布，其作用不仅限于式（4）中项，式（4）中滑裂面上的土体剪应力项及抗剪力项都反映了锚固结构和和土体共同作用的结果。

由式（3）可以看出，在有限元强度折减法安全系数的计算中，仅对地层的抗剪强度指标C和φ值用安全指数FS持续收敛，以有限元计算中力和位移无法趋于某一稳定值视为失稳发生的条件。即锚杆参与了整个有限元分析过程，而有限元强度折减法并没有对锚固结构自身的强度进行换算，因此锚固结构发挥了比土体强度不折减时更大的加固作用，导致在一定程度上高估了锚固结构的加固效果。

因此，上述原因在稳定性评价的结果上表现为：两类有限元计算所得滑动稳定系数较大，滑裂面也更深。

3 结论

（1）研究分析表明，结合极限平衡条分法对锚固边坡滑动安全系数的定义，采用有限元极限平衡法对锚固边坡进行稳定性评价是行之有效的。

（2）采用极限平衡条分法进行锚固边坡稳定分析时，由于条间力假设的存在以及对锚固结构加固效应考虑不全面，从而导致同有限元方法相比，安全系数较小且滑裂面较浅。

（3）有限元强度法对锚固边坡进行稳定分析时，由于仅考虑土体强度参数的折减，未对锚固结构强度进行折减，同另外两种方法相比，或导致在一定程度上高估了锚固结构的加固效应，在三种方法所得稳定性分析结果上则表现为，有限元强度折减法的安全系数最大且滑裂面也最深。

[1]钱家欢, 殷宗泽. 土工原理与计算[M]. 北京: 水利水电出版社, 1993.

[2]陈祖煜. 土质边坡稳定分析[M]. 北京: 中国水利水电出版社, 2003.

[3]郑颖人, 赵尚毅. 用有限元强度折减法求边（滑）坡支挡结构的内力[J]. 岩石力学与工程学报, 2004, 23（20）: 3552-3558.

[4]韦立德, 叶志华, 陈从新, 等. 一种锚杆计算模型及其在岩坡锚杆支护中的应用[J]. 岩土工程学报, 2008, 30（5）: 732-738.

[5]刘文连, 韦立德. 强度折减有限元法中锚杆计算模型研究[J]. 岩土力学, 2010, 31（12）: 4021-4026.

[6]施建勇, 曹秋荣, 周璐翡. 修正有限元强度折减法与失稳判据在边坡稳定分析中的应用[J]. 岩土力学,2013,34（2）: 237-241.

[7]白冰, 袁维, 石露, 等. 一种双折减法与经典强度折减法的关系[J]. 岩土力学, 2015, 36（5）: 1275-1281.

[8]薛海斌,党发宁,尹小涛,等. 边坡强度参数非等比例相关联折减法研究[J]. 岩土力学与工程学报, 2015, 34（2）: 4005-4012.

[9]A.Isakov, Y. Moryachkov. Estimation of slope stability using two-parameter criterion of stability[J]. International Journal of Geomechanics，2014，14（3） : 1–3.

[10]邵龙潭,唐洪祥,韩国城. 有限元边坡稳定分析方法及其应用[J]. 计算力学学报，2001，18（1）: 81-87.

[11]于斯滢,邵龙潭,刘士乙. 基于有限元极限平衡法的尾矿坝坝体稳定分析[J]. 岩土力学，2013，34（4）:1185-1190.

[12]邵龙潭,刘士乙. 极限平衡条件的拓展与土工结构稳定分析 [J]. 岩土力学，2015，36（1）： 71-75.

Stability Analysis of Anchored Soil Slope Based on Finite Element Limit Equilibrium Method

CHONG Ji-xin

（Jinan Rail Transit Group Co.,Ltd., Shandong Jinan 250101, China）

Under the condition of plane strain, the finite element limit equilibrium method has been used studying some key question of stability analysis for anchored slope. The definition of slices method’ s safe factor is generalized to FEM. The“ true” stress field of integral structure can be got by elastic-plastic finite element analysis, then finish the optimal search for most dangerous sliding surface with Hooke-Jeeves optimized searching method. Three examples of stability analysis of natural slope, anchored slope with seepage and excavation anchored slope are proposed. The difference of safety factor quantity, shape and location of slip surface, anchoring effect among slices method, strength reduction finite element method (SRM) and finite element limit equilibrium method are contrastive analyzed. The safety factor given by the FEM was greater than that of the slice method and the unfavorable slip surface was deeper.The finite element limit equilibrium method has great calculation accuracy, and to some extent, the slice method underestimates the effect of anchor, on the contrary, the SRM overrates.

anchored slope; finite element limit equilibrium method; strength reduction FEM; stability