基于实测资料的南海海浪波高和周期联合分布研究
黄必桂, 金嘉萌, 胡 琴, 谢波涛
(中海油研究总院,北京 100028)
基于实测资料的南海海浪波高和周期联合分布研究
黄必桂, 金嘉萌, 胡 琴, 谢波涛
(中海油研究总院,北京 100028)
海浪波高和周期联合分布关系是海洋工程设计的重要参数,尤其对浮式结构设计更加重要。目前波高和周期的联合分布已有大量理论模型和经验模型。基于南海北部海区长达1年的实测波高和周期数据,对多种波高和周期联合分布理论模型和经验模型进行适应性分析。研究结果表明:Longuet-Higgins模型、C.N.E.X.O.模型、孙孚模型和郑桂珍改进模型等理论模型与实测数据相比存在一定偏差;Bitner-Gregersen波高和周期的经验模型较为适用于南海北部海域。同时还通过参数拟合得到南海波高周期联合分布曲线,该结果可为南海海洋工程设计提供参考。
波高;周期;联合分布;概率密度函数
0 引 言
海浪波高和周期的联合分布对海洋学研究和海洋工程设计具有理论和实用价值,可以用波高和周期的联合分布去推导获得其他联合分布(如波高和坡度的联合分布)[1],也可以为海洋工程结构计算提供波高和周期的联合分布关系,以保障设施安全。在海洋浮式设施设计中,波高周期联合分布关系成为海洋浮式平台等设施的重要设计参数。
针对海浪波高与周期联合分布关系开展过广泛的研究,并随着理论研究的进步和观测资料的增加,研究成果逐渐完善。早期因理论水平和资料的限制,认为波高和周期是两个相互独立的随机变量,在该假定下提出过波高与周期的联合概率密度为波高概率密度和周期概率密度的乘积。但在实际观测中发现波高和周期不完全独立,尤其在波高和周期较小的条件下,相关性很高[2]。
随后从理论出发推导得到的波高与周期联合概率分布函数也取得较为丰富的研究成果。1975年Longuet-Higgins[3]在窄谱假定下,首先提出与谱宽参量ν有关的波高与周期的联合分布,该分布相对于无因次周期t=1对称。1978年Goda[4]依观测资料绘出了窄谱条件下波高与周期的联合分布图,结果表明波高与周期联合分布是不对称的,从而证明1975年Longuet-Higgins提出的分布模型不准确。随后,1983年Longuet-Higgins[5]对其早期提出的模型进行了修正,引入归一化因子对,提出了波高与周期非对称的联合分布函数。1976年Cavanié等[6]也从理论上提出了非对称性的波高周期分布函数,此时的分布函数与谱宽参数有关。1987年中国学者孙孚[7—8]在线性海浪模式及波动的射线理论基础上推导出一种波高与周期的联合分布。此后的学者在上述理论的基础上开展了大量研究工作,提出了一些改进的波高周期联合分布模型[9]。
与此同时,有一些学者应用概率定理建立了波高与周期的联合分布经验函数,并利用实测资料或者实验室资料进行验证[10—11]。其中一些成果已被海洋工程的规范所引用[12]。
关于波高周期联合分布关系在外海和近岸已开展了较多的研究[13—14],但在南海开阔海域,研究海浪波高和周期联合分布的成果还较少。本文利用南海北部油气田区长达1年的海浪波高周期观测数据,研究了南海北部海域波高周期联合分布关系,为海洋工程开发设计提供参考。
1 海上观测数据介绍
“863”计划课题(2008AA09A401)在南海北部海域进行了波浪观测,观测设备为波浪骑士,观测站位于南海某油气田区(见图1)。观测区域水深约200m,有效数据时间为2011年6月—2012年5月。
波浪骑士观测的数据涵盖本文所使用的全部数据,包括有效波高、多种波浪周期和波浪谱宽参数等。详细的波浪骑士参数可参见“基于实测资料的南海海浪周期关系研究”一文[15]。
数据观测期间涵盖了2个台风过程和冬季风过程,数据较为全面。
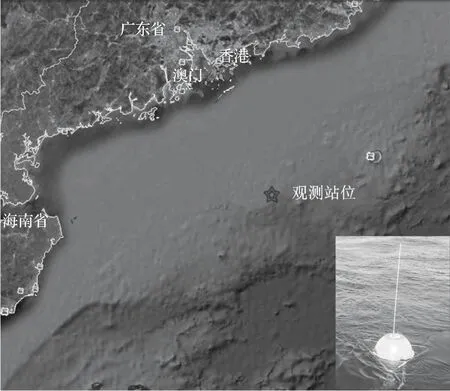
图1 观测站位及观测设备示意图[15]Fig.1 Sketch map of the observation site and the buoy
2 波高周期联合分布理论模型分析
2.1 Longuet-Higgins模型
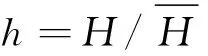
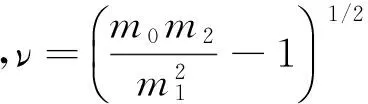
随后1983年Longuet-Higgins[5]引入归一化因子,对上述模型进行了修正,提出新的无因次波高和无因次周期的联合分布函数:
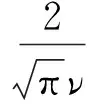
(2)
式中:L(ν)为正则因子,L(ν)=2/[1+(1+ν2)-1/2],h=H/Hrms。
本文利用南海海上观测数据,对Longuet-Higgins模型进行验证。图2为观测谱宽参数ν的柱状图,从中可以看出,ν主要分布于0.3~0.5之间,均值为0.42。
图3为Longuet-Higgins1983年提出的波高周期分布与海上观测波高周期数据散点分布。从图中可以看出,Longuet-Higgins模型与实际观测存在一定的差异,在小波高处,周期分布范围过宽。
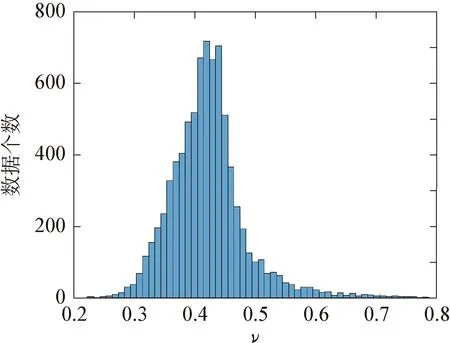
图2 观测期间谱宽参数ν柱状图Fig.2 Histogram of spectrum width ν during the observation period
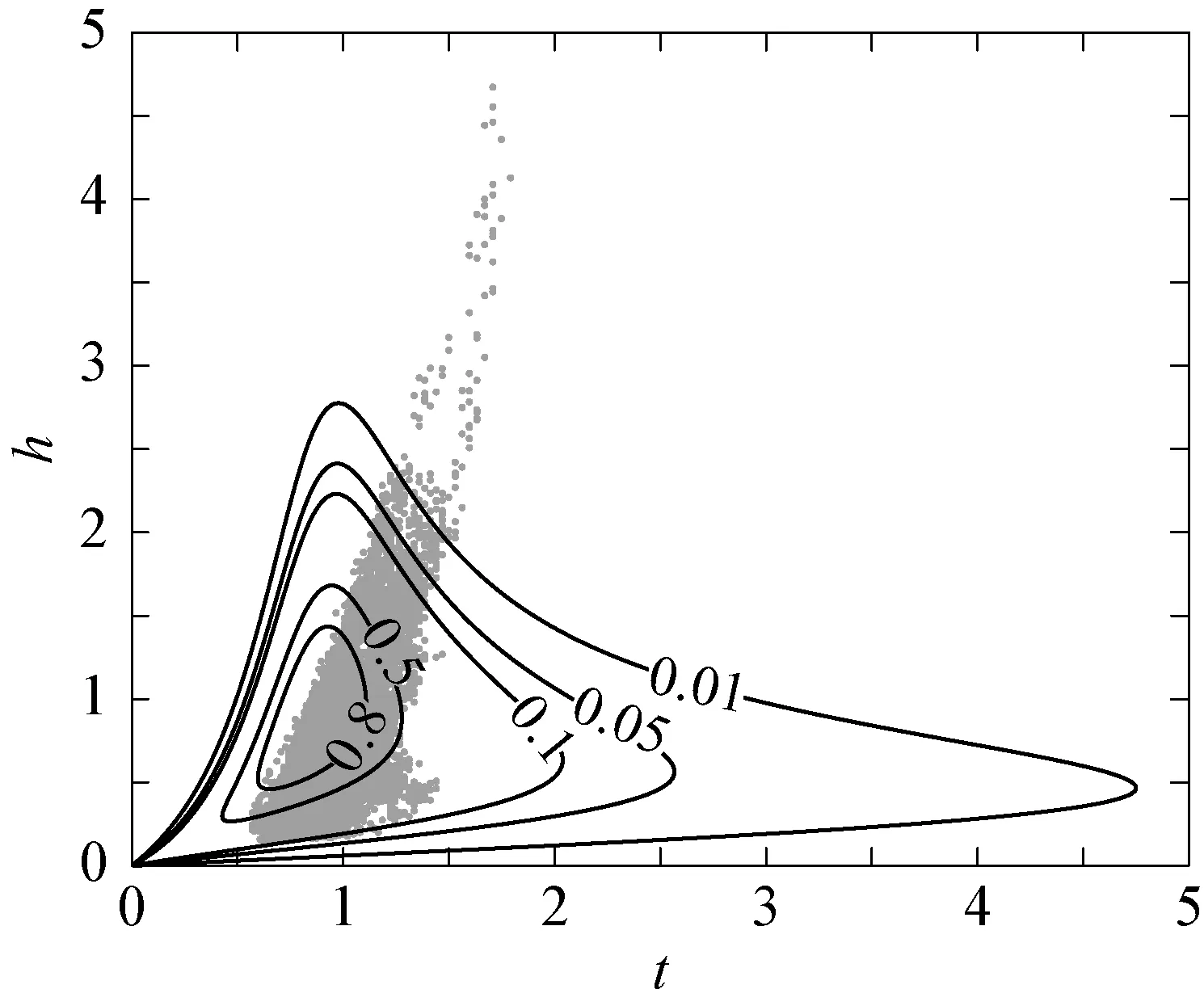
图3 Longuet-Higgins模型与实测数据的散点分布Fig.3 Comparison of Longuet-Higgins model and scatter diagram of measured data
2.2 C.N.E.X.O.模型
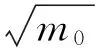
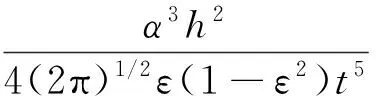
(3)
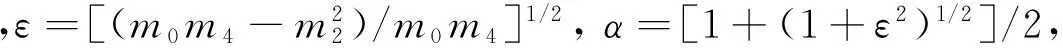
图4为观测期间谱宽参数ε的柱状图,从中可以看出,ε主要分布于0.6~0.8之间,均值为0.71。
图5为C.N.E.X.O.模型的波高周期分布与海上观测波高周期数据散点分布。从图中可以看出,C.N.E.X.O.模型与观测总体趋势较为一致,克服了Longuet-Higgins模型在小波高处周期过宽的问题,但是C.N.E.X.O.模型存在总体偏左问题,而且周期最宽位置过高。
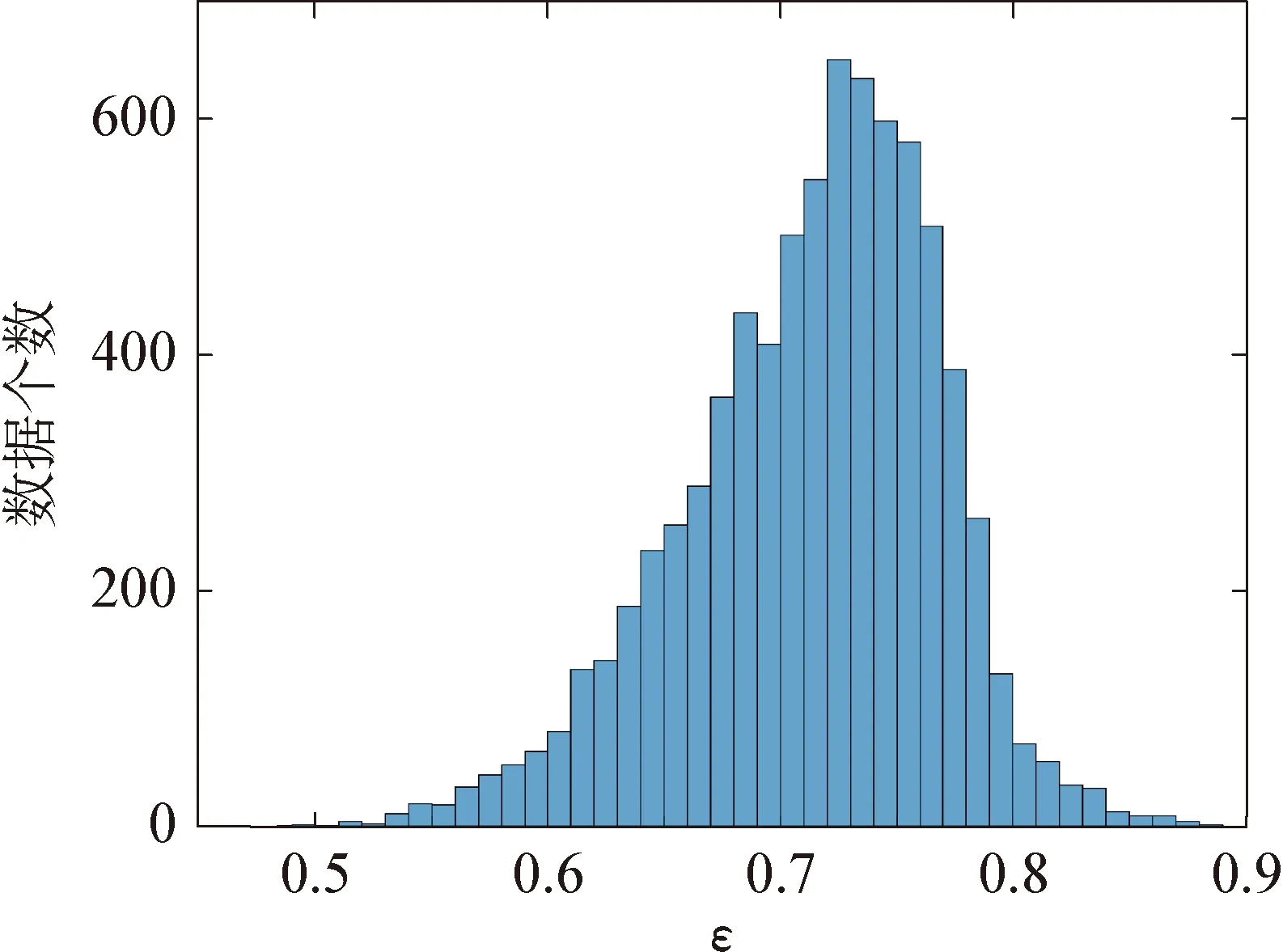
图4 观测期间谱宽参数ε柱状图Fig.4 Histogram of spectrum width ε during the observation period
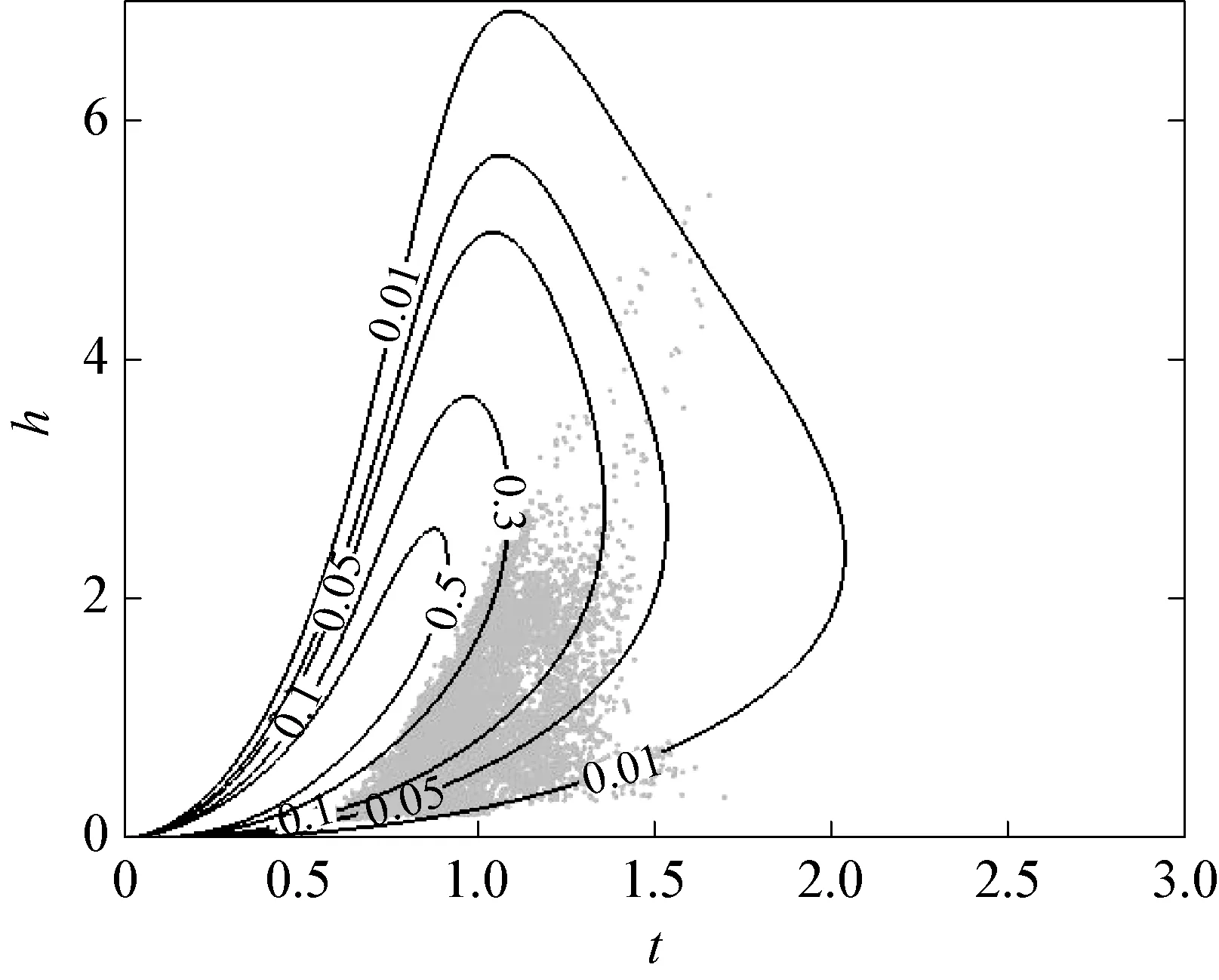
图5 C.N.E.X.O.模型与实测数据的散点分布Fig.5 Comparison of C.N.E.X.O. model and scatter diagram of measured data
2.3 孙孚模型
1987年孙孚[7]对1983年的Longuet-Higgins模式进行了改进,提出新的无因次波高h=H/(2πm0)1/2与无因次周期t=T/2π(m0/m1)的联合概率密度函数:
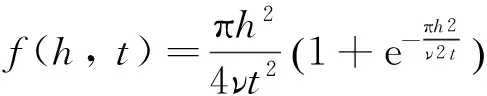
(4)
图6为孙孚模型的波高周期分布与海上观测波高周期数据散点分布,从图中可以看出,孙孚模型存在与Longuet-Higgins模型类似的问题,即在小波高处周期分布过宽的问题。
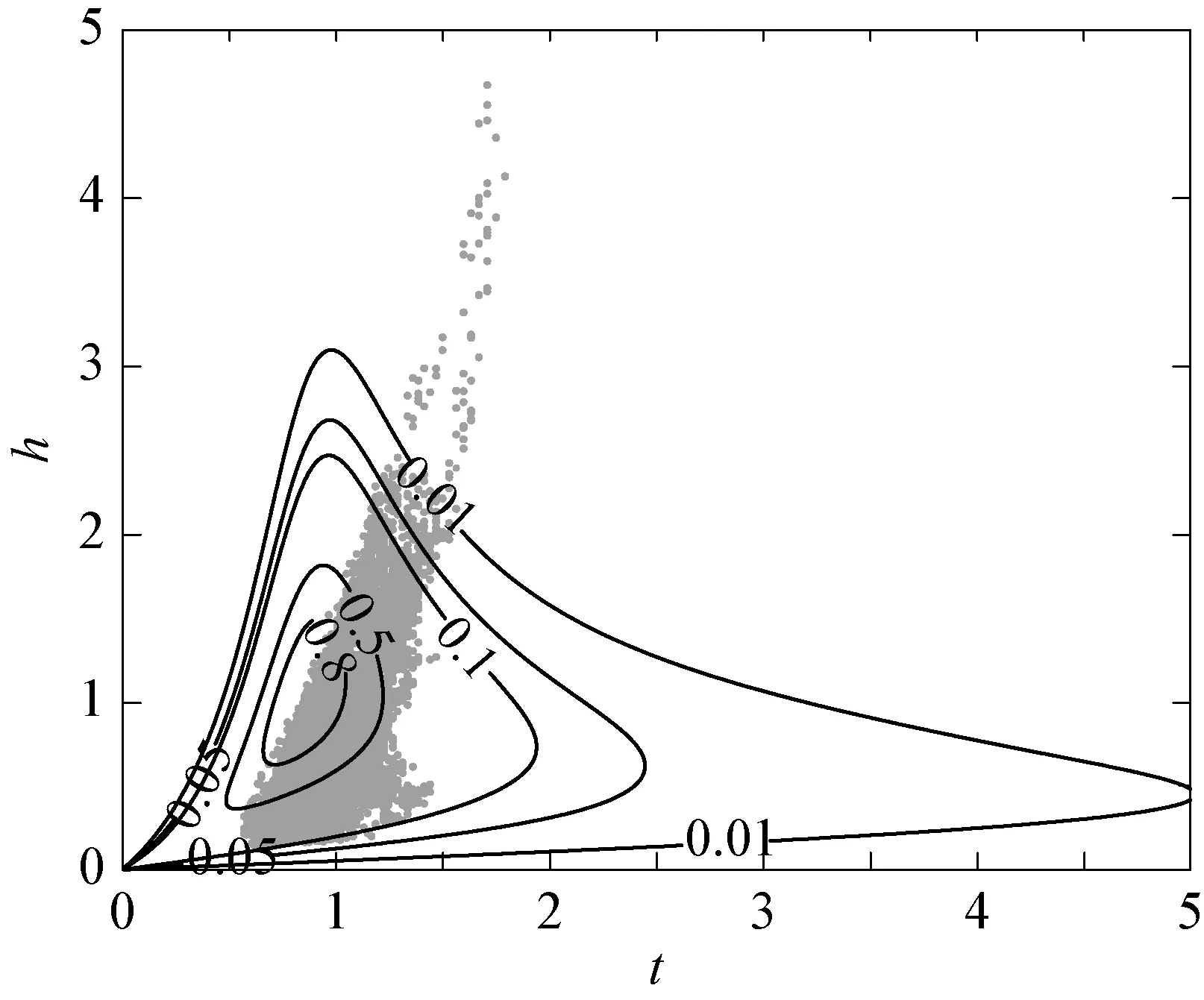
图6 孙孚模型与实测数据的散点分布Fig.6 Comparison of Sun model and scatter diagram of measured data
2.4 其他改进理论模型
2004年郑桂珍等[9]在Longuet-Higgins和孙孚模型的基础上,进行理论研究,提出了改进的无因次波高与无因次周期的概率密度模型,其概率密度函数为
(5)
式中:h=H/(8m0)1/2;无因次周期t=T/2π(m0/m1)。
图7为郑桂珍改进模型的波高周期分布与海上观测波高周期数据散点分布。从图中可以看出,该模型对Longuet-Higgins和孙孚的问题有了较大的改进,避免了在小波高处周期过宽的问题,但是总体上还存在曲线偏左的问题。
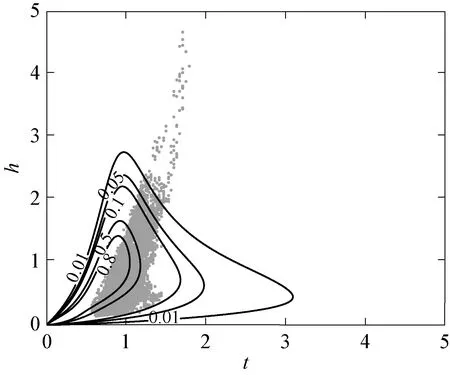
图7 郑桂珍改进模型与实测数据的散点分布Fig.7 Comparison of Zheng model and scatter diagram of measured data
3 波高周期联合分布经验模型分析
一些学者应用概率定理建立了波高与周期的联合分布函数,提出波高与周期联合概率密度函数为波高概率密度函数与周期的条件概率密度函数的乘积,即f(h,t)=f(h)·f(t|h),但对波高概率密度和周期条件概率密度分布有不同的结论[10—12]。
关于波高的概率密度函数,大量学者经过研究和观测数据检验,大都认为波高服从Rayleigh或者三参数Weibull分布。周期条件概率密度函数服从高斯分布或者对数正态分布。
图8为本次观测的有效波高的概率密度分布与三参数Weibull分布和Rayleigh分布对比,从图中可以看出,该海区的有效波高服从三参数Weibull分布,即
(6)
图9为本次观测的周期条件概率密度分布(hs=1~2m)。从图中可以看出,周期条件概率密度与高斯分布和对数正态分布的符合度都很高(概率密度曲线几乎重合),通过K-S检验,结果表明对数正态分布的符合度更高。对数正态分布的概率密度函数如下:
(7)
对上式中的μ和σ, Bitner-Gregersen[16]经过实测资料研究,推荐了以下关系:
μ=E[lnt]=a0+a1ha2,
(8)
σ=std[lnt]=b0+b1eb2h.
(9)
针对Bitner-Gregersen提出的波高周期关系,利用实测数据进行参数拟合,得到的波高周期联合分布曲线与散点图见图10。从图中可以看出,波高周期联合分布等值线与实测波高周期散分布非常接近。
在图10的曲线拟合过程中,首先用式(6)对波高进行三参数Weibull拟合,得到波高的概率密度函数,其次借助式(8)和式(9),利用波高和周期的实测数据,拟合出式(8)和式(9)中的各参数,从而可得到式(7)的周期条件概率,最后用式(6)和式(7)相乘得到波高和周期的联合分布。
同时,图10中的波高周期联合分布曲线是在该海区连续1年的观测数据条件下拟合得到的,观测数据包含了冬季季风海况、夏季台风海况以及其他一般海况等条件,因而图10中的曲线能适用该海区的多种海况条件。
此外,Bitner-Gregersen的波高周期联合分布经验模型还可针对实测的有效波高和实测周期进行拟合,不用对实测数据进行无因次化,从而更方便应用于工程设计。
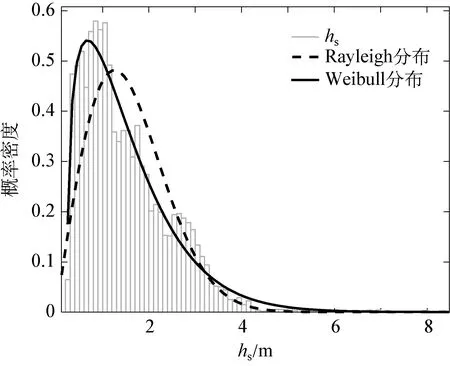
图8 有效波高概率密度分布Fig.8 Probability density distribution of significant wave heights
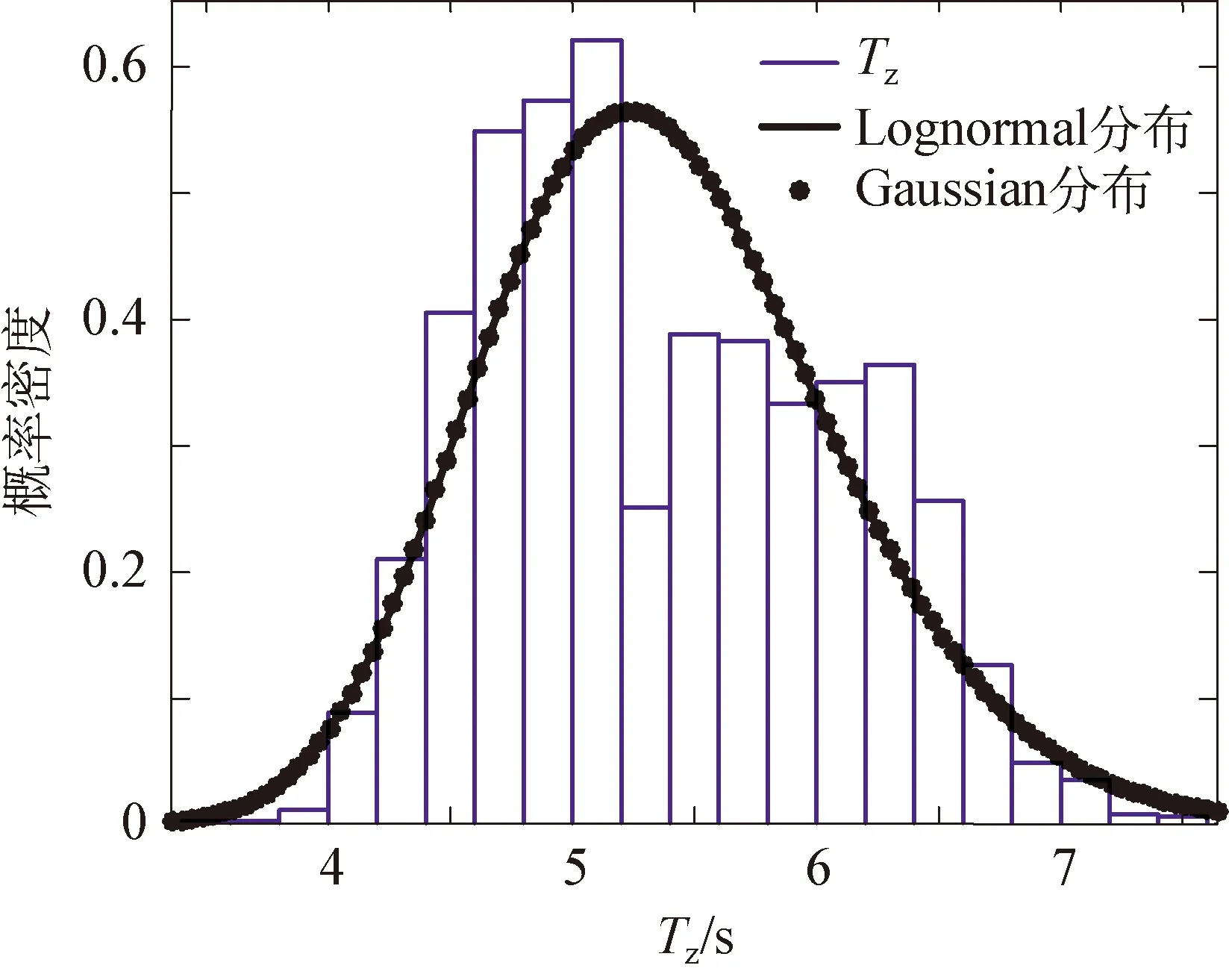
图9 跨零周期条件概率密度分布Fig.9 Conditional probability density distribution of zero crossing periods
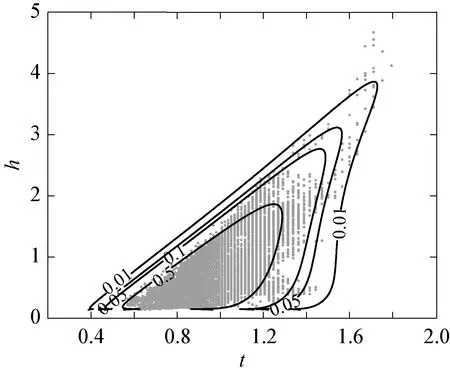
图10 Bitner-Gregersen模型与实测数据的散点分布Fig.10 Comparison of Bitner-Gregersen modeland scatter diagram of measured data
4 结 语
本文借助南海北部海区实测的波浪数据,分析了该海区波高周期散点分布和谱宽参数,同时对多种海浪波高周期联合分布模型进行了分析和检验。结果表明:
(1) 南海北部海区,谱宽参数ν主要分布于0.3~0.5之间,均值为0.42;谱宽参数ε主要分布于0.6~0.8之间,均值为0.71。
(2) 在海浪波高周期联合分布理论模型中,与实测数据相比,Longuet-Higgins模型和孙孚模型在小波高处,存在周期分布范围过宽问题;C.N.E.X.O.模型存在总体偏左(波高偏小),而且周期最宽位置过高问题;郑桂珍模型存在总体偏左(波高偏小)问题。这些模型不推荐直接应用于海洋工程设计。
(3) Bitner-Gregersen波高周期联合分布经验模型通过参数拟合,能较好地反映南海北部海区波高周期联合分布关系,经过实测数据拟合得到的波高周期联合分布曲线,可为海洋工程设计提供参考。
[1] Doering J C, Donelan M A.浅水波波高和周期的联合分布[J].海岸工程,1997,16(3): 63.
Doering J C, Donelan M A. The joint distribution of heights and periods of shoaling waves [J]. Coastal Engineering, 1997,16(3): 63.
[2] Chakrabarti S K, Cooley R P. Statistical distribution of periods and heights of ocean waves [J]. Journal of Geophysical Research Atmospheres, 1977,82(9): 1363.
[3] Longuet-Higgins M S. On the joint distribution of wave periods and amplitudes of sea waves [J]. J. Geophys. Res. 1975,80: 2688.
[4] Goda Y. The observed joint distribution of periods and heights of sea waves [C]. Proc. 16th Int. Conf. on Coastal Eng., 1978: 227.
[5] Longuet-Higgins M S. On the joint distribution of wave periods and amplitudes in a random wave field [J]. Proceedings of the Royal Society of London A, 1983,389: 241.
[6] Cavanié A, Arhan M, Ezraty R.A statistical relationship between individual heights and periods of storm waves [C]. Proc. Conf. on Behav. Offshore Struct., 1976,2: 354.
[7] Sun F. On the joint distribution of the periods and heights of sea waves [J]. Acta Oceanologica Sinica, 1987,6(4): 503.
[8] 孙孚.海浪周期与波高的联合分布[J].海洋学报,1988,10(1): 10.
Sun Fu. Study on the joint distribution of wave periods and heights [J]. Acta Oceanologica Sinica, 1988,10(1): 10.
[9] Zheng G, Jiang X, Han S. The difference between the joint probability distributions of apparent wave heights and periods and individual wave heights and periods [J]. Acta Oceanologica Sinica, 2004,23(3): 399.
[10] 吴秀杰,郭洪梅,赵炳来,等.浅水海浪周期与波高联合分布函数的确定[J].海洋学报,1981,3(4): 517.
Wu Xiu-jie, Guo Hong-mei, Zhao Bing-lai, et al. Determination of joint distribution function of wave periods and heights of the shallow sea [J]. Acta Oceanologica Sinica, 1981,3(4): 517.
[11] 葛明达.连云港波高周期统计分布[J].海洋工程,1984(1): 40.
Ge Ming-da. Distributions of wave heights and periods in Lianyun Harbour [J]. Ocean Engineering, 1984(1): 40.
[12] Det Norske Veritas. DNV-RP-C205. Environmental conditions and environmental loads [S]. 2014.
[13] GuedesSoares C, Carvalho A N. Probability distributions of wave heights and periods in combined sea-states measured off the Spanish coast [J]. Ocean Engineering, 2012,52: 13.
[14] 潘锦嫦,陈志宏.海浪波高与周期联合概率密度分布的研究[J].海洋通报,1996,15(3): 1.
Pan Jin-chang, Chen Zhi-hong. Study of the joint probability density distribution of wave heights and periods [J]. Marine Science Bulletin, 1996,15(3): 1.
[15] 黄必桂,石新刚,谢波涛,等.基于实测资料的南海海浪周期关系研究[J].海洋学研究,2016,34(3): 6.
Huang Bi-gui, Shi Xin-gang, Xie Bo-tao, et al. Study on the relationships of ocean wave periods in the South China Sea based on the observed data [J]. Journal of Marine Sciences, 2016,34(3): 6.
[16] >Bitner-Gregersen E M. Joint probabilistic description for combined seas [C]. ASME 2005 International Conference on Offshore Mechanics and Arctic Engineering, 2005: 169.
StudyontheJointDistributionofWaveHeightsandPeriodsintheSouthChinaSeaBasedonObservedData
HUANG Bi-gui, JIN Jia-meng, HU Qin, XIE Bo-tao
(CNOOCResearchInstitute,Beijing100028,China)
The joint distribution of wave heights and periods is an important design basis of ocean engineering design, especially for floating structure design. Many theoretical models and empirical formulae for joint distribution of wave heights and periods have been proposed. In this paper, 1-year measured wave heights and periods data in north of the South China Sea are applied to examine the joint distribution models of wave heights and periods. The results show that the theoretical models of Longuet-Higgins, C.N.E.X.O., Sun and Zheng are not suitable to the South China Sea, while the empirical model of Bitner-Gregersen is suitable to this area. Additionally, the parameters of the Bitner-Gregersen formula are calibrated, and the contour of wave height and period is plotted. The results can be applied to the ocean engineering design in the South China Sea.
wave height; wave period; joint distribution; probability density function
P731.22
A
2095-7297(2017)04-0187-06
2017-03-31
国家“863”计划(2008AA09A401);南海油气区海洋工程设计中的风谱及风速时距关系研究课题(2017-JZKT-15);海上油气田开发海洋环境影响研究(YXKY-2016-ZY-07);新型高重现期设计方法工程应用程序(2016OT-GC58);海洋大功率往复式压缩机总体方案研究课题;多点系泊FPSO装置CTV卸油方式研究课题
黄必桂(1984—),男,硕士,高级工程师,主要从事海洋工程环境条件及设计标准方面的研究。

