TA误差分段拟合算法的分段点选取方法

周雪青，张岩坡，李铁成，李安昌

(1.国网河北省电力有限公司电力科学研究院，石家庄 050021；2.国网河北省电力有限公司检修分公司，石家庄 050071)

TA误差分段拟合算法的分段点选取方法

周雪青1，张岩坡2，李铁成1，李安昌1

(1.国网河北省电力有限公司电力科学研究院，石家庄 050021；2.国网河北省电力有限公司检修分公司，石家庄 050071)

介绍三次样条插值和指数函数分段拟合算法，针对算法中存在分段点选择的不同直接影响TA传变误差计算精度的问题，提出利用斜率系数法实现三次样条插值和指数函数拟合时分段点选择的方法，通过实例验证，说明该方法可提高算法的拟合精度，更加准确的描述线性区和饱和区伏安特性。

电流互感器；分段拟合；分段点；斜率

电网发生短路故障，电流互感器可能发生饱和，饱和后TA的一、二次电流已非正常的线性关系，传变误差将超过相关规程规定的允许值，误差过大将导致继电保护在原设定保护范围内误动或拒动[1-5]。因此通过电流互感器的伏安特性数据，验算电流互感器误差是否满足要求，具有重要意义。TA误差分段拟合算法是利用三次样条插值和指数函数综合解析表达式拟合伏安特性曲线[6]，可计算出TA一次侧大短路电流，特别是越限短路电流时的精确误差值、10%误差曲线和二次最大允许负载。然而算法中利用现场伏安特性试验数据时，由于试验数据只能做到TA饱和点附近，无法直接得到短路故障时对应的励磁电流。因此算法中由于分段点选择的不同使伏安特性曲线呈现不同的拟合趋势，从而对应不同的励磁电流数值，使计算结果误差较大。因此通过大量现场试验数据计算比对，以下提出斜率系数法来确定拟合算法的分段点，可准确描述线性区和饱和区伏安特性，计算结果准确，具有广泛的工程应用价值。

1 三次样条插值和指数函数分段拟合算法

三次样条插值(Cubic Spline Interpolation)是通过一系列值点的光滑曲线，数学上通过求解三弯矩方程组得出曲线函数组的过程。实际计算时还需要引入边界条件才能完成计算，只能保证各小段曲线在连接点的连续性，曲线在边界点外拟合趋势不准确，即在伏安特性饱和区的曲线趋势不能满足工程计算要求。指数函数如式(1)。

(1)

两边取对数可转化为一次方程形式y=ax+b。以y和x绘制的散点图呈直线趋势时，可考虑采用指数函数来描述U2和I2间的非线性关系。指数函数能很好地拟合伏安特性饱和区的曲线趋势，但是其函数本身的特点决定不能描述伏安特性的完整过程。为了克服三次样条插值法在伏安特性饱和区的曲线趋势和指数函数不能描述伏安特性的完整过程两类局限性，考虑到TA大短路电流时励磁绕组的饱和特性，而工程实际中又想得到完整的伏安特性曲线，采用基于三次样条插值和指数函数分段拟合的算法，综合解析表达式拟合伏安特性曲线，可计算出当流过TA一次侧短路电流时的误差值和10%误差曲线。

2 分段拟合算法分段点选取存在的问题

2.1 TA伏安特性数据

以河北省南部电网某220 kV变电站内220 kV断路器TA为例，TA型号为LB9-220W2，其中铭牌参数为5P30，2 500/5，30 VA，一次侧短路电流为30.36 kA。归算到75°的二次直阻为1.35 Ω，二次负载为1.67 Ω。 根据现场测试数据获取TA伏安特性试验数据，如表1所示。

表1 TA伏安特性试验数据

I2/AU2/VI2/AU2/V0.12823.02950.32835.03000.5284103051.028615307

根据表1中数据可知，二次侧电流与电压一一对应，二次电流值越大，TA饱和程度越高。

2.2 随机选取分段点

利用三次样条插值和指数函数分段拟合的算法对表1中试验数据进行分段拟合，若随机选取第3个点(0.5 A，284 V)作为分段点，即第1至第3个点使用三次样条插值算法拟合，第3至第8个点使用指数函数拟合算法，其拟合的伏安特性曲线如图1所示。

图1 伏安特性曲线(分段点为3)

根据图1可知，由于拟合点选取不当，从第3个点开始，TA的伏安特性曲线还未进入饱和区，指数函数不能很好的拟合伏安特性非饱和区的曲线趋势，导致第7和第8个点严重脱离拟合曲线，不符合伏安特性拟合要求。TA误差值计算如下式：

(2)

式中：If表示系统发生短路故障时TA的励磁电流，m10表示短路电流倍数，I2N表示二次额定电流。其中，m10的值等于短路故障时一次电流I1与一次额定电流为I1N的比值。

由式(2)求出以第3个点作为分段点时的TA误差值为31.22%，二次最大允许负载为1.27 Ω。

若随机选取第7个点(10 A，305 V)作为分段点，进行曲线拟合，其拟合的伏安特性曲线如图2所示。

图2 伏安特性曲线(分段点为7)

由图2可知，当电流增加至50 A时电压增加的过大，拟合的曲线末端过高，不能准确描述TA的饱和特性。这是由于在第7个点之前，TA的伏安特性曲线已经进入饱和区，而三次样条插值算法不能很好的拟合出饱和区的曲线趋势，不符合伏安特性拟合要求。同理，可求出以第7个点作为分段点时的TA误差值为26.7%，二次允许负载为1.35 Ω。

而且，在工程实际中现场试验可能会出现“坏点”现象，即某个电压电流点离散度较大，偏离预定轨迹，不符合TA的伏安特性。这样在进行分段拟合求取误差值时可能会出现图3所示情况。

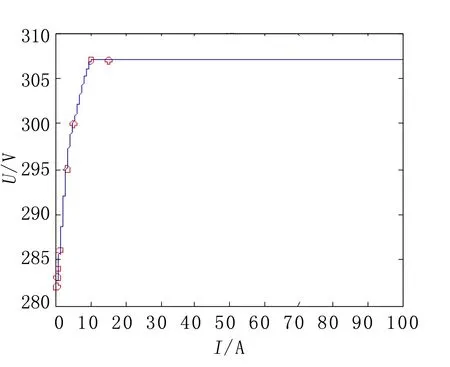
图3 伏安特性曲线(坏点)

由图3可知，由于第7个点出现“坏点“现象，而随机选择的分段点导致拟合效果非常不合理。

根据以上分析，随机选取分段点，可能会使非饱和区的试验数据参与指数函数算法拟合，也可能会使饱和区的数据参与三次样条插值算法拟合，导致拟合效果不理想，TA误差值不准确。

另外，在进行河北省南部电网220 kV以上TA伏安特性分析和误差校核时，需要面对数以千计的TA和大量试验数据。如何从每组TA数据中准确的选取分段点进行分段拟合，使误差校核工作快速精准，是我们亟待解决的问题。

3 分段点选取方法

3.1 斜率系数法的提出

针对以上问题，通过分析大量的伏安特性试验数据发现，相邻数据的斜率会在某一点处发生较大变化，由伏安特性导致的斜率会由较大数值突变为较小数值，据此可作为伏安特性线性区域与饱和区域的分界点。引入方差的概念如下式：

D(X)=(X-E(X))2

(3)

式中：X表示随机变量，E(X)表示期望，D(X)表示方差，用来表示数据的偏离程度，描述数值波动情况。根据现场伏安特性数据进行相邻点斜率计算，对斜率这组数据逐步进行方差计算，数值越小说明越稳定，当数值突变较大时说明与均值离散程度变高，TA开始呈现饱和特性，可由此得到分段点。

3.2 利用斜率系数法选取分段点

对表1中每2个相邻数据进行斜率计算和方差计算，如表2所示

表2 斜率和方差

KDKD5.002.51.0755.001.02.5674.00.3330.43.6634.50.229//

通过表2可看出，不论是斜率K值还是方差D值，在第5个点都有了很大变化，前后比值变高，K4/K5=1.8 ，D4/D5=4.69 ，说明该TA的伏安特性在第5个点开始进入饱和状态，即选择第5个点为分段点，如图4所示。

由图4可知，选择合适的分段点使伏安特性的线性区和饱和区都得到了很好的描述，拟合程度高，能够准确拟合伏安特性走向，反应TA饱和趋势和程度。此时TA误差值为28.44%，二次最大允许负载为1.30 Ω。

由以上可知，选择分段点不同，不仅伏安特性曲线有偏差，而且TA的误差值和二次允许负载值也会有变化。所以正确选择分段点对于TA的误差校核是至关重要的。通过对河北南网大量试验数据进行比对计算，提出斜率系数：

图4 伏安特性曲线

Kn/Kn+1≥1.5

(4)

Dn/Dn+1≥3

(5)

当斜率系数首次满足如上2个条件时，对应的伏安特性试验数据可以作为分段点，这样拟合精度高，误差计算快速准确。

4 应用情况及效果

目前，按照《国网河北省电力有限公司关于加强TA应用管理的通知》相关要求，河北省南部电网TA误差校核工作需每年开展完成。基于三次样条插值和指数函数分段拟合算法中利用斜率系数法实现分段点的选择可以精确计算TA传变误差，其计算方法已在河北省南部电网得到广泛应用，能够很好拟合实测数据。通过对TA短路情况下的误差计算，可对TA进行是否超差评估，加强对TA的管控能力，提高该运行设备状态水平，增加保护的可靠性。当评估出TA超差时，应予以措施解决，包括限值一次系统短路水平、增大保护TA变比、减小TA二次负载、更换抗饱和特性较好的TA等措施，为河北省南部电网各供、发电企业TA的整改和更换提供依据。

5 结束语

以上针对TA误差计算时的三次样条插值和指数函数分段拟合算法存在的弊端，提出斜率系数法对算法中的分段点自动进行选择，可准确描述TA的伏安特性，计算出不同短路故障情况下的精确误差值和二次最大允许负载，有效评估TA的超差水平。该算法已应用于河北省南部电网多个变电站的TA误差分析工作中，计算快速、准确，能够提高工作效率，在工程应用方面具有推广价值。

[1] 袁季修，盛和乐，吴聚业．保护用电流互感器应用指南[M]. 北京: 中国电力出版社, 2004.

[2] Q/GDW 690-2011，电子式互感器现场校验规范[S].

[3] 陈丽艳,何奔腾,钱国明,等.基于二次电流下降的电流互感器饱和判别方法[J]. 电力系统自动化, 2008, 32(14): 59-63.

[4] 郭耀珠,石 光,刘 华,等.保护用电流互感器10%误差曲线现场测试及其二次负载校核[J]. 电力系统保护与控制, 2008, 36(23): 101-104.

[5] 张健康, 粟小华,胡 勇,等.智能变电站保护用电流互感器配置问题及解决措施[J].电力系统保护与控制, 2014,42(7): 140-145.

[6] 周雪青，郝晓光，张岩坡，等．基于分段拟合算法的电流互感器误差研究[J]．电力系统保护与控制，2017，45(3)：139-143．

Segmented Point Selection Method of TA Error Subsection Fitting Algorithm

Zhou Xueqing1,Zhang Yanpo2,Li Tiecheng1,Li Anchang1

(1.State Grid Hebei Electric Power Research Institute, Shijiazhuang, 050021 China;2.State Grid Hebei Electric Power Maintenance Company, Shijiazhuang 050071,China)

This paper introduces the subsection fitting algorithm of three spline interpolation and exponential function.Aiming at the difference of the segmentation selection in the algorithm directly affecting the calculation accuracy of TA transmission error,this proposes the slope coefficient method to realize the segmented point selection of three spline interpolation and exponential function algorithm,After improves the fitting accuracy and more accurately describe the linear and saturation regions of I-V character through.

current transformer;subsection fitting;segmentation point;slope coefficient

2017-07-29

周雪青(1987-)，女，工程师，主要从事电力系统继电保护工作。

TM452

B

1001-9898(2017)06-0048-04

本文责任编辑：王丽斌