数形结合 发展学生数学思维
陈 波
(浙江省宁波市鄞江中学,浙江宁波 315100)
引 言
高中学习知识和以前学习的知识有所差别,在以前的基础上上了很大的一个台阶,这尤其体现在高中数学上,其中复杂的解题思路更是成了数学中的难题。在数学教学中,函数换元思想是一种非常重要的数学解题方法。函数换元就是将复杂的数学表达或复杂的数学思想进行替换,通过替换转换了一种思想,一种解题思路,从而让学生对学习数学产生兴趣,只要巧用一些数学思想,学习高中数学会变得简单些。
一、以形助数,联结数与式
一直以来,数形互变就是所有老师最为提倡的一种解题方法,这种方法在高中数学中更是体现得淋漓尽致。教师应该采取适当的方法设计课程,寓数于形,以形于数来帮助学生解决抽象的数学问题,从而提高学生学习兴趣,将高中数学学习到极致。
1.转化斜率,求最值
数与形是数学中的两个最古老,也是最基本的研究对象,它们在一定条件下可以相互转化。中学数学研究的对象可分为数和形两大部分,数与形是有联系的,这个联系称之为数形结合,或形数结合。在解题的时候,如何运用图形来更快更准确地解决数学题,是好多学生不能感受到的解题思路。
为了让学生能深刻地体会与掌握数形结合这种数学思路,我设计了这样的课程。例如,已知:图1有向线段PQ的起点P与终点Q坐标分别为P(-1,1),Q(2,2)。若直线l∶x+my+m=0与有向线段PQ延长相交,求实数m的取值范围。在求解这道题的时候直线l的方程x+my+m=0可化为点斜式:y+1=-1/m(x-0),易知直线l过定点M(0,-1),且斜率为-1/m。
因为:l与PQ的延长线相交,由数形结合可得:当过M且与PQ平行时,直线l的斜率趋近于最小;当过点M、Q时,直线l的斜率趋近于最大。在给同学们讲解题方法的时候,比如说上面的例子,可以巧妙地根据题目已知条件,常常可以根据数形结合的思路,转化为求解斜率的问题,有效地把复杂问题进行简单化,将抽象的问题进行具体化,在解决高中生数学题的时候具有较为重要的指导意义。
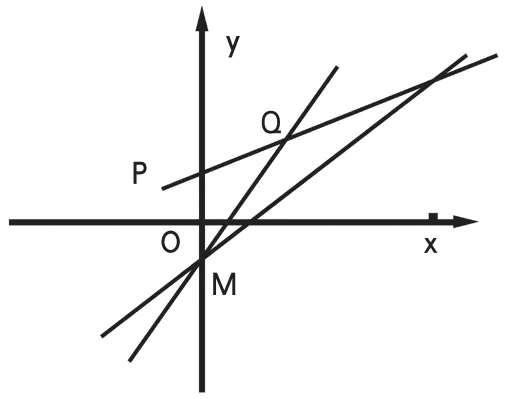
图1
2.构造函数,解方程
同学们在解一些高中函数题目的时候,常常可以根据题目已知条件结合自己所学的知识,画出题目所给的函数的图像,然后将函数转化为方程或者方程组,通过构造函数解方程或方程组。
比如在给同学们讲解这道题的时候,题目是:若关于x的方程||x-2|-1|=a有三个整数解,则a的值是[ ]首先我让同学们画了图像如图2所示:
其中:方程||x-2|-1|=a的解是函数y=||x-2|-1|的图像与y=a的图像交点的横坐标,所以原方程有三个整数解的条件,即转化为函数y=||x-2|-1|的图像与y=a的图像有三个公共点。作y=||x-2|-1|的图像。因为y=a的图像是平行于x轴的直线,从图像知,当y=a的图像过点(0,1)时,两图像才有三个交点(其横坐标是整数),此时a=1。
构造函数或者构造方程,结合图像可以很轻松地解决掉数学问题中的一些疑难杂症,比如说在所给问题中本质上是关于学过的函数问题,或者是学过的方程,可以考虑构造辅助函数和方程,使得问题得以解决。
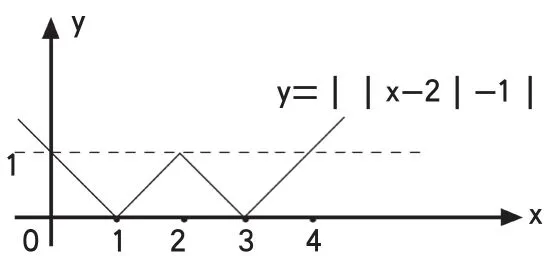
图2
二、以数辅形,解决几何题
在数学这门科学中,数学理论形式可以通过一定的图形将数学理论展现出来,从而将有些数学问题简单化。同样的,有时将图形数字化也会起到简化数学的作用,将图形从形象化到数据的定量分析,会在解决实际问题起到事半功倍的效果。
1.分析数据,证中有算
高中数学,无疑在以前数学学习的基础上上了一个台阶,这使许多学生立马感到学习的难度,遇到图形题时更是无从下手。这时,以形变数,将图形问题定量化分析,会使学习数学不那么困难。
比如我就此观点设计了这样一道例题,让学生深深地体会到以形变数的重要性。f(m)=m2-2nm+2,条件当m在[-1,+∞],f(m)>n恒成立,求n的取值范围。通过分析可以发现f(m)>n恒成立,即可以写成m2-2nm+2-n>0恒成立。令g(m)=m2-2nm+2-n,此时画出g(m)的图形在m在[-1,+∞]的情况下都是大于0都在x轴的上方。此时,运用图形显然不能解决这道题,于是换个角度讲,如此时利用判别式这个数学方法来做,问题就迎刃而解了。通过这题的解答可以看出,虽然图形可以直观地展示出来,让我们直观地看出来,但对于一些涉及量化的知识图形就做不到了,此时借助一些特有的数字公式或结论,会使问题变得无比简单。
2.建坐标系,测量距离
在数学中,数学家笛卡尔发明了坐标。它具有重大的研究意义,主要在于使数学的基本研究对象:数和形得到统一。所以利用坐标系集合数形结合的思想,既可以用运算这种处理数的方法,方便地处理图形,也可以用图形的特性,直观地解释函数的性质,所以说,坐标系是数形结合的利器。
比如说在讲解关于空间直角坐标系这道题的时候,如果直接给学生讲解答案,他们可能会一下子反应不过来,但如果以图形作为载体,在图形上直观地表现出已知条件以及尽可能地画出所要求的答案,同学们就可以很容易地理解了。这道选择题是这样的:以棱长为1的正方体ABCD-A1B1C1D1的棱AB、AD、AA4所在的直线为坐标轴,建立空间直角坐标系,则平面AA1B1B对角线交点的坐标为( )。
A.(0,0.5,0.5) B.(0.5,0,0.5)
B.(0.5,0.5,0) D.(0.5,0.5,0.5)
在给同学们讲解的时候,我首先指导同学们画出由已知条件所给的空间直角坐标系,然后根据所要求的,先将答案在图上标出来,所画的图形如图3所示。
由这个图形可以很直观地看出平面AA1B1B对角线交点是横坐标为AB的中点值,竖
坐标为AA1的中点值,纵坐标为0,所以平面AA1B1B对角线交点的坐标为(0.5,0,0.5)。故选 B。
“数形转换”就是根据“数”与“形”既对立又统一的特征,通过观察图形的形状,分析数与式的结构,引起联想,适时将它们相互转换,化抽象为直观并提示隐含的数量关系。从而更好地应用在数学解题中的一种方法。

图3
三、数形串联,突出综合性
以数化形是数学解题中最常用的一种方法,学生在理解那些抽象性比较高的数量关系时可能有一定的难度,无法形成深刻的理解和认识,学习效果不理想。此时若引入“形”这一解题思路,通过直观的图形将数学难题展现出来,那么学生学习就不再感到有压力了。
1.深度观察,寻找互变条件
作为数学一种较为重要的思想方法,数形结合的应用大致又可分为两种情形:或者借助于数的精确性来阐明形的某些属性;或者借助形的几何直观性来阐明数之间某种关系。
在数学解题中,遇到难的数字化太强的题目,无从下手时,不妨试着换个思路,将数字转化为图形,说不定就柳暗花明了。“以数解形”就是有些图形太过于简单,直接观察却看不出什么规律来,这时就需要给图形赋值,如边长、角度等。
2.梳理关系,明晰解题缺口
数形结合,可以深度梳理题目中的相关关系,准确地抓住题目的解题缺口,比如:从一些题目的解题过程可以看出,有时候综合使用“数形转换”,理解数形转换的实质,遇到实际问题从数形转换着手,就一定在有限的时间解出问题。
例如在给同学们讲解下面这道例题的时候,就运用了数形结合的方法,利用图形深度梳理题目中的已知条件,将已知与未知联系起来。这道题是这样的:已知点(3,5)M,在y轴和直线y,x上分别找一点P和N,使得MNP△的周长最小。
我给同学们在讲解这道题目前的时候,画了直角坐标系,将已知条件和未知条件都尽可能用图形表示出来,图形如图4所示。在图像上,作点(3,5)M,关于y轴和直线y=x的对称点 12M1M2,则点 12 M1M2的坐标分别为 (-3,5),(5,3)。

图4
根据已知条件,可以整理式子得:x+4y-17=0,即是直线M1M2的方程,它与y轴和直线y=x的交点分别可以得到(0,17/4),(17/5,17/5),即可以得到△MNP周长最小的点P和N的坐标分别为(0,17/4),(17/5,17/5)。
这道题,主要利用了数形结合的思想,梳理了题目中的已知条件,并且利用“对称关系”,几种思想相互结合,明确这道题到底在考什么,将问题转化为两点之间线段最短的问题,巧妙地解开了问题。
结 语
总而言之,数形结合思想作为一种重要的数学思想,在高中数学解题中起到了至关重要的作用,学生灵活地使用它可以将抽象复杂的数学知识生动、形象地展示出来,从而降低了学生理解数学题的难度,拓展了学生的思维,也提升了学生的解题能力。因此,教师在教学中,要积极合理地引入数形结合思想,积极培养同学们的数学发散性思维,让数形结合在教育道路上越走越远!
[1] 徐先荣.谈初中数学数形结合的教学策略[J].考试周刊,2007(04).
[2] 冉正伟.浅谈在高中数学教学中如何渗透数形结合思想[J].科学咨询,2012(06).
[3] 杨云美.数形结合的高中数学教学策略及实现[J].语数外学习,2013(07).
[4] 张福庆.例谈高中数学数形结合解题法教学的有效策略[J].高中数理化,2013(16).

