面向供水管网水力模型自动校核问题的改进遗传算法①

刘佳明,王 宁,徐浩广

1(中国科学院 沈阳计算技术研究所,沈阳 110168)

2(中国科学院大学,北京 100049)

面向供水管网水力模型自动校核问题的改进遗传算法①

刘佳明1,2,王 宁1,徐浩广1,2

1(中国科学院 沈阳计算技术研究所,沈阳 110168)

2(中国科学院大学,北京 100049)

水力模型自动校核旨在提高供水管网智能化管理中模型的准确性,目前广泛使用遗传算法进行自动校核.针对标准遗传算法收敛速度慢,并且容易陷入局部最优解的问题,本文对标准遗传算法进了改进,利用模拟退火法对适应度函数进行了拉伸,采用轮盘赌和最优保留策略相合的方法代替传统的选择方法,在交叉操作中加入了相似度函数避免了近亲杂交,并且使用双重收敛判断准则减少不必要的计算时间. 引入G市某区域供水管网水力模型为案例,使用改进后的遗传算法进行自动校核. 结果表明,改进的遗传算法求解效率和求解精度都有较大的提高.

水力模型自动校核; 遗传算法; 改进遗传算法; 供水管网

随着供水管网智能化管理的普及,各城市开始投入大量人力和财力构建或完善管网水力模型. 供水管网水力不仅可以用于水厂优化运营管理、供水调度,还可以成为其它相关研究的基础,如管网水质模拟、突发性水质污染事件预警与定位等. 水力模型自动校核是指通过程序自动调整模型中预先设置的水力参数,使模型计算值与监测值匹配的过程,其目的在于使构建的水力模型能更准确的模拟管网的真实运行状态,达到预期使用的目的. Preis等[1]提出使用遗传算法进行水力模型自动校核,并得到普遍应用.

遗传算法是借鉴生物进化理论和群体遗传学思想,演变发展起来的一种具有应用性广泛、快捷方便的随机搜索技术的优化算法. 其编码技术和遗传操作比较简单,对优化问题的限制性条件要求低,具有很强的鲁棒性和内在的并行计算机制. 但它容易出现早熟现象和收敛速度慢的问题,导致不能获得全局最优解[2].

近年来国内外学者对遗传算法的改进做了很多研究工作. Kuo[10]提出了具有破坏性选择的遗传算法,通过使用最优策略选择出优秀的个体和淘汰低劣的个体,能加快了种群的进化速度. De Jong[11]则使用自适应交叉和变异算子使算法能朝全局最优解的方向进行搜索.Goldberg等人[12]则将在简单的遗传算法中加入局部搜索机制——贪心算法,用来解决模糊寻优问题. 国内也很多学者对遗传算法进行了改进研究,陈长征、王楠[13]对变异和交叉概率进行改进,能够克服算法的早熟问题. 杨旭东[14]设计了自适应选取适应度函数的方法,避免了算法的局部收敛. 这些研究工作对遗传算法的发展有着重要意义,为本文的研究奠定了良好的基础.

本文结合供水管网水力模型自动校核问题,针对标准遗传算法收敛速度慢,并且容易陷入局部最优解的问题,对标准遗传算法进行了改进,利用模拟退火法对适应度函数进行了拉伸,采用轮盘赌和最优保留策略相合的方法代替传统的选择方法,在交叉操作中加入了相似度函数避免了近亲杂交,并且使用双重收敛判断准则减少不必要的计算时间. 最终引入G市某区域供水管网水力模型为案例,使用改进后的遗传算法进行自动校核. 结果表明,改进的遗传算法求解效率和求解精度都有较大的提高.

1 管网水力模型自动校核原理及问题建模

1.1 影响供水管网水力模型准确性的因素

(1) 管网基础数据的准确性

在供水管系统模型中,要进行水力计算,那么就必须要以大量的数据作为基础,比如管网布置图; 管道的长度、直径、材料; 节点的方位、高低; 阀门的类别、大小、开启程度、位置; 水库或者水塔的大小、水位等都包括在内. 除此之外,水泵的运行曲线、停启情况都包括在内. 管网水力模型的好坏与庞大而精准的数据有直接的关系,并在此基础上创建水力模型. 其中所涉及到的数据是大而全面的,供水企业要将如此大量的数据进行管理是非常困难的,一般情况下,在进行数据的存储时,使用数据库或是GIS系统,这样就能够让数据的管理变得简便.

(2) 管网拓扑图形的完善性

管网拓扑图实际上并没有将所有的管段都包含在内,一些直径教小的,不会过多的影响到水力条件的小管段都会在管网拓扑图中进行相应的减少或者是合并.但是,考虑到部分关键性小管段进行减少或者是合并后,在一定程度上影响到下游压力,那么这样做就是不合适的. 并且,有些管段的改变还会对水流的方向产生一定的影响,这些也是不能够简化的.

(3) 管网节点流量的不确定性

在计算管网的水力时,会进行虚拟节点流量的设计,这也是为了简便出发的. 通常节点的流量就是管段流量的随机集中,这样就使得计算分配具有一种随机性. 在进行计算时,采用这一方法可以说大大的简化了程序,但是从实际的情况看来,还是有很大差距的,也会对管网的计算产生很大的影响,这样所设计的模型是与实际的管网不相符合的. 假如出现流量用户与节点分配错误的情况,那么将会非常严重的影响到局部的压力分布以及管段流量分布.

(4) 管段摩阻系数的不确定性

对于供水管网管段的摩阻系数进行测量时,通常实际测量只是能够将一些具有代表性以及易于测量的部分进行准确的测量,很多的管段都是不能够进行有效测量的,一般对于不能测量的管段,会通过管段自身的属性来进行进一步的摩阻值估算. 估算的结果实际上是不精确的.

1.2 供水管网水力模型自动校核问题建模

利用建模软件EPANET2.0建立供水管网水力模型[3],并手工核实基础数据后,利用管网上的压力监测点的实测值与模型的计算进行比较,对水力模型中的不确定参数(节点流量和管段摩阻系数)进行调整,使得误差满足要求为止. 建立数学模型如下:

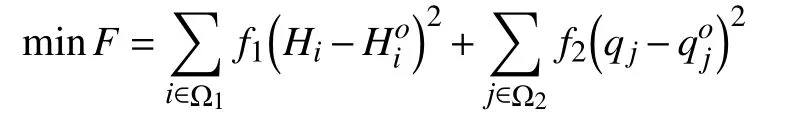
约束条件为:

f1,f2——分别为节点压力和节点流量的量纲影响系数;

Ω1,Ω2——压力监测点和管段监测点的集合;

q——管段流量转置矩阵;

q=(q1,q2,...,qn)T,单位为 m3/s;

Q——节点流量转置矩阵,Q =(Q1,Q2,...,Qn)T,单位为m3/s;

h——管段水头损失转置矩阵,h= (h1,h2,...,hn)T,单位为m;

Qr——管段总供水量,单位为m3/s;

A,L——连续性方程和能量方程系统矩阵;

C——海曾-威廉系数;

K——节点流量变化系数;

Hmin——各节点的最低水压要求,单位为m;

n,P——分别为节点数和管段数.

F表示的水力模型的误差,用遗传算法求解时,作为目标函数. 遗传算法流程图如图1所示.

随着经济科技的发展,供水管网上安装了大量的传感器并引入SCADA系统,水力模型的更新周期也就大大缩短,用传统的遗传算法进行校核已满足不了实时性. 所以提高算法效率是非常必要的.

2 改进遗传算法设计

文献[3]中采用标准遗传算法对该模型进行求解,标准遗传算法对参数要求高,收敛速度慢且容易陷入局部最优解中,下面则结合该模型的特点对标准遗传算法进行了改进.

2.1 染色体编码

在水力模型校核中,每个节点流量和管段C值为一个基因,全体基因(所有节点流量和管段C值)构成一个染色体,若干个染色体组成一个种群,遗传操作以种群为单位进行,最终选出种群中最优的染色体就作为问题的最优解. 原有的二进制编码用双精度实数编码进行取代,这样就能够改善由于海明距离的影响而造成二进制编码表达困难的问题,从而整体上将编码解码的效率提升,无论是在精度上,还是在速度上,交叉与变异都得到了提升,实数编码通过如下的方式实现.

2.2 初始化群种

在解空间内随机生成N个染色体作为初始种群,每个染色体表示供水管网中所有不确定的管段摩阻系数C值和用户节点的流量的编码组合,N为种群的规模. 理论上种群规模越大包含的信息越丰富,更容易生成最终的优良个体,但是种群规模越大,算法计算的代价也越大,因此一般取变量个数的线性级别,如有10个变量则N的取值范围为10～100.

2.3 适应度函数

遗传算法中,适应度是体现个体在生存环境中的适应程度,表征个体的优劣性,适应度高的个体将会获得更多的机会去产生后代,反之会在进化中逐渐灭绝.在本文模型中,适应度f可以由目标函数值F转化而来,目标函数值表示水力模型的误差,值越小说明水力模型越精确. 而遗传算法是努力将基因的适应度函数最大化,因此将适应度函数设定为目标函数的倒数即:f=1/F. 然后在遗传算法后期,当算法趋于收敛时,由于种群中个体适应度差异较小,继续优化的潜能降低,常有可能获得局部最优解. 为此,本文利用模拟退火法(SA)对适应度函数进行拉伸[4],避免个体的早熟现象.

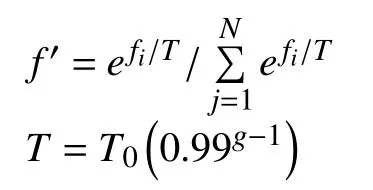
式中:fi——第i个个体的适应度;

g——遗传代数序号;

N——种群个体数;

T——温度;

T0——初始温度.

T值随着进化次数g的增加而减少,当g<30时,T=1.5×0.9g,否则T=0.01.

2.4 遗传操作

2.4.1 选择操作

选择操作是种群进行过程中优胜劣的手段,个体适应度大的个体,其被选择的概率越高,反之更可能被淘汰[5]. 标准的遗传算法一般使用轮盘赌方式进行行选择操作,但是在算法执行过程中,若初始群体中存在一些适应度比较好的个体,用轮盘赌方式这部分个体会繁殖更多的后代,占据了后代种群的主要部,而对于一些适度度较差的个体则会陷入灭绝的境地,如此就会破坏了种群的多样性,导致算法陷入早熟收敛. 本文采用轮盘赌方式和最优保留策略相结合的方法,步骤如下:

1) 首先求种群的平均适应度以及每个个体的适应度.

2) 如果个体的适应度大于种群的平均适应度,则保留下来,否则使用轮盘方法进行选择.

3) 比较保留下来的适应度最好的个体与截止目前找到的最好个体的适应度值,比较大的那个个体作为新的截至目前最好的个体.

4) 将上一步找到的最好的个体不参与交叉和变异操作直接放到子代种群的第一位,其余的保留的个体进行交叉和变异操作.

这样,不仅没破坏种群的多样性,而且还会向着最优解的方向搜索,提高了运算效率.

2.4.2 交叉操作

如果其值小于阀值0.001p,说明双亲为近亲. 这样就避免了由于近亲杂交而产生不良个体,保证遗传操作的正常进行.

2.4.3 变异操作

变异操作是模拟生物进化过程的基因突变现象,用来保证种群的多样性,防止早熟[7]. 在遗传算法中,变异一般被看作为辅助算子,它作用在染色体上以较小概率Pm随机改变染色体上的某个基因. 本文在算法初期加大变异概率,使搜索空间更广阔,在算法后期降低变异概率,防止算法变成随机搜索不会收敛.

2.5 双重收敛判断准则

在设计遗传算法的收敛准则时,一般采用设定总的进化次数I为收敛依据,一旦进化次数达到I,就可以终止程序的运行. 但是,如果在算法执行的过程中,初始群体以及其它参数选取非常理想的情况下,那么遗传算法可以很快的搜寻到最优解. 这种情况下,如果再采用总的进化次数I为收敛准则,就增加了不必要的计算时间[8]. 因此在算法执行过程中,本文采用双重收敛判断准则:

(1) 总的进化次数I;

(2) 连续多次进化的优化结果不变,或优化结果小于某一提前设定的固定的小数ε.

在遗传算法进化过程中,满足上述两个条件中的任何一个,都视为满足收敛条件. 这样的收敛准则就可以适当减少不必要的计算时间.

3 案例应用与结果分析

以G市某区域供水管网为例,建立相应的水力模模型,引入SCADA数据库中监测值. 供水管网GIS图见图2,供水管网中有13压力监测点和6个流量计,在校核之前水力模型在24个时间段的平均压力和流量误差情况为表1所示.

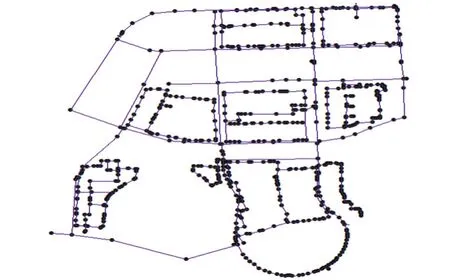
图2 G 市某区域供水管网 GIS 图

表1 水力模型压力误差统计

用标准遗传算法和本文设计的改进遗传算法分别对水力模型进行自动校核,调整供水管网水力模型中不确定的管段摩阻系数C值和用户节点流量. 算法的各个参数设置如下: 初始种群大小N为300,迭代次数I为 100,ε为 0.1,交叉概率Pc为 0.8,变异概率Pm为0.05. 校核后,水力模型精度分别如表2 和表3 所示,算法的运行情况如图3.

改进的遗传算法相比于标准遗传算法对水力模型自动校核结果更精确,另外标准遗传算法难收敛到某一解,运行的时间也较长,而改进后的算法能跳出局部最优,找到更好的解,并且运行的时间也有较大的提高.

为证明改进算法的通用性,本文还选取了10个管网水力模型分别用和标准遗传算法和改进的遗传算法进行自动校核. 方法过程与G市相同,结果统计如图4和图5所示.

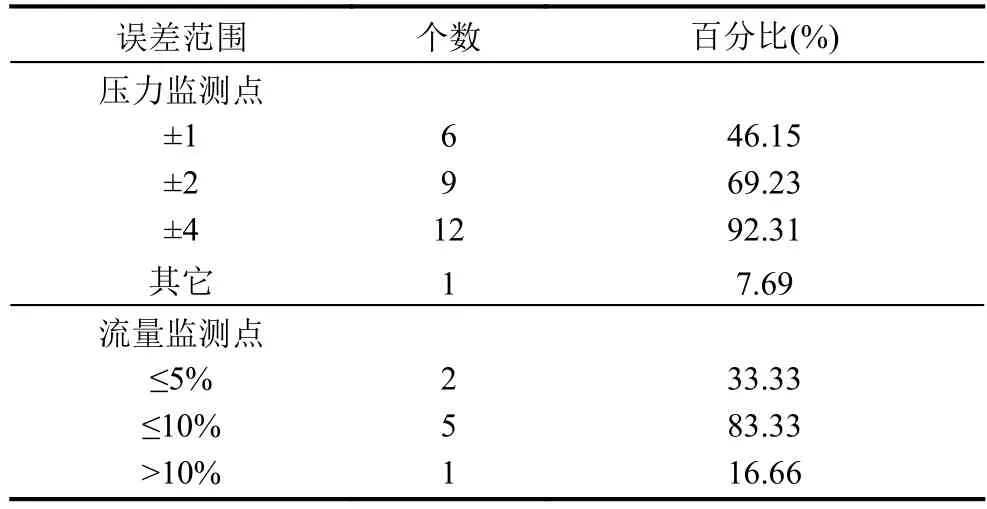
表2 标准遗传算法校核后水力模型误差统计

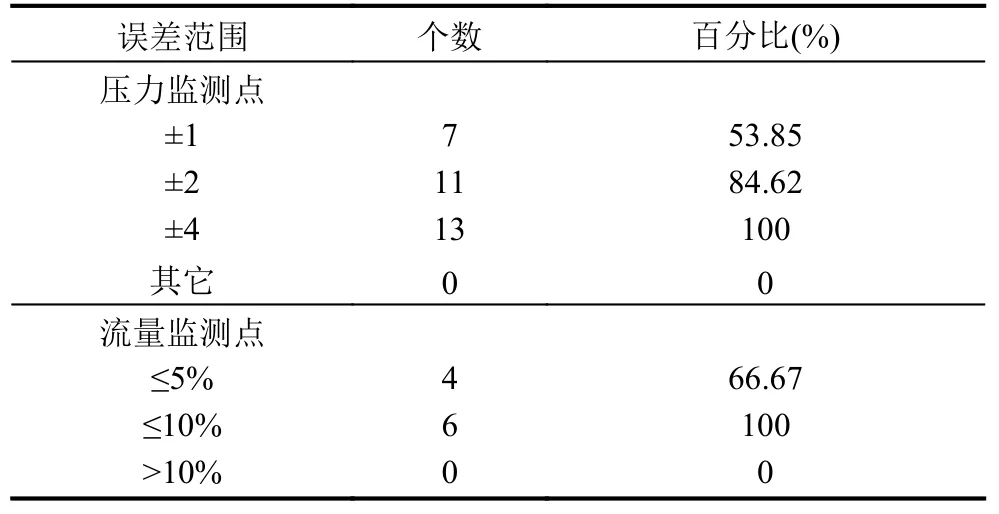
表3 本文改进遗传算法校核后水力模型误差统计

图3 两种算法的运行情况

图4 10 次测试收敛次数比较

由对比图可以发现,改进的算法无论在收敛次数还是在收敛时间方面都有较大的提高.

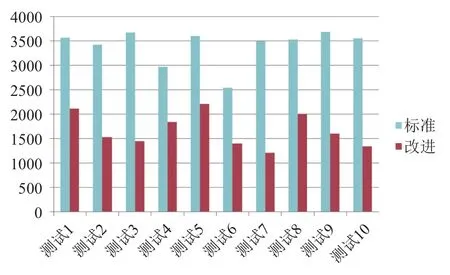
图5 10 次测试收敛耗时比较 (单位: s)

4 结论

本文对供水管网水力模型自动校核问题进行了描述,并建立了问题模型,针对标准遗传算法求解效率低并且容易陷入局部最优解的情况,采用改进的适应度函数、选择操作、交叉操作、变异操作以及使用双重判断收敛准则重新设计了算法,最后引入实际案例分别用标准遗传算法和改进算法进行求解,并对结果进行了比较分析,验证了改进的效果. 但用本文改进的遗传算法对大型供水管网水力模型自动校核需要数小时,对要求实时进行校核的供水管网水力模型仍难以满足,因此如何大幅度提高遗传算法的运行时间有待下一步研究.

1Preis A,Allen M,Whittle AJ. On-line hydraulic modeling of a water distribution system in Singapore. Proc. of the 12th Annual Conference on Water Distribution Systems Analysis(WDSA). Singapore. 2012. 1336–1348.

2曳永芳,杜永清,行小帅. 一种抑制早熟收敛的改进遗传算法. 山西师范大学学报 (自然科学版),2010,24(2): 24–28.

3孙柏. 供水管网水力水质模型及其校核研究[硕士学位论文].长沙: 湖南大学,2012.

4姚明海,王娜,赵连朋. 改进的模拟退火和遗传算法求解TSP 问题. 计算机工程与应用,2013,49(14): 60–65. [doi:10.3778/j.issn.1002-8331.1211-0133]

5史明霞,陶林波,沈建京. 自适应遗传算法的改进与应用.微计算机应用,2006,27(4): 405–408.

6吉根林. 遗传算法研究综述. 计算机应用与软件,2004,21(2): 69–73.

7琚洁慧. 改进适应度函数的遗传算法. 电脑知识与技术,2005,(15): 80–83.

8李书全,孙雪,孙德辉,等. 遗传算法中的交叉算子的述评.计算机工程与应用,2012,48(1): 36–39.

9周松儒. 遗传算法的混合改进研究及其应用[硕士学位论文].南宁: 广西大学,2014.

10Glodberg DE,Kuo CH. Genetic algorithms in pipeline optimization. Computing in Civil Engineering,1987,1(2):128–141.

11Jong KAD. An analysis of the behavior of a class of genetic adaptive systems. University of Michigan,1975.

12Goldberg DE. Genetic Algorithms in Search,Optimization,and Machine Learning. Massachusetts: Addison-Wisley,Reading,1989.

13陈长征,王楠. 遗传算法中交叉和变异概率选择的自适应方法及作用机理. 控制理论与应用,2002,19(1): 41–43.[doi: 10.3969/j.issn.1000-8152.2002.01.007]

14杨旭东,张彤. 遗传算法应用于系统在线识别研究. 哈尔滨工业大学学报,2000,32(1): 102–105. [doi: 10.3321/j.issn:0367-6234.2000.01.027]

Improved Genetic Algorithm for Automatic Calibration of Water Supply Hydraulic Model

LIU Jia-Ming1,2,Wang Ning1,XU Hao-Guang1,2

1(Shenyang Institute of Computing Technology,Chinese Academy of Sciences,Shenyang 110168,China)
2(University of Chinese Academy of Sciences,Beijing 100049,China)

The automatic calibration of hydraulic model aims to improve the accuracy of the model of water supply network intelligent management. Currently,the genetic algorithm is widely used for automatic of hydraulic model. In view of problems that the standard genetic algorithm has slow convergence and can be easily trapped in local optimal,the paper makes some improvements of this algorithm. Simulated annealing algorithm is used to stretch the fitness function and the roulette wheel selection method combining elitism strategy is replacing the traditional selection method. Besides,the similarity function is added to avoid the breeding with closest relatives in cross operator and the double convergence criteria is used to reduce unnecessary computation time. The improved genetic algorithm is used to calibrate the water supply hydraulic model of G. The results show that the improved genetic algorithm has better efficiency and accuracy.

automatic calibration of hydraulic model; genetic algorithm; improved genetic algorithm; water supply network

刘佳明,王宁,徐浩广.面向供水管网水力模型自动校核问题的改进遗传算法.计算机系统应用,2017,26(12):104–109. http://www.c-sa.org.cn/1003-3254/6069.html

辽宁省科技计划-环境预警项目(20150303)

2017-03-03; 修改时间: 2017-03-20; 采用时间: 2017-03-27