蜂窝铝冲击波形数值计算及分析

曹 杰,葛建立,王 浩,杨国来

(南京理工大学 机械工程学院,江苏 南京 210094)

蜂窝铝冲击波形数值计算及分析

曹 杰,葛建立,王 浩,杨国来

(南京理工大学 机械工程学院,江苏 南京 210094)

为分析蜂窝铝结构参数以及弹丸参数对冲击波形的影响,利用LS-DYNA有限元软件建立了弹丸侵彻蜂窝铝模型,模拟了侵彻波形的发生过程。比较了蜂窝铝相对密度、胞孔角度,侵彻初速和弹头形状对冲击加速度波形的影响。结果表明,增大蜂窝铝相对密度、减小胞孔角度可以引起加速度峰值的提高和冲击脉宽的减小;提升初始侵彻速度可以同时引起加速度峰值与脉宽的提升;弹丸形状影响冲击波形,使用卵形弹可以获得较平缓的加速度波形。研究结果对以蜂窝铝为缓冲材料的冲击试验参数选择具有重要参考价值。

蜂窝铝;胞孔构型;弹丸;冲击波形;峰值;脉宽;有限元

在航空航天领域,大量的内部器件、二次仪表面临不同的加速度环境考核。尤其当飞机失事出现坠机,飞行记录仪会经历强冲击载荷。在设备的研制过程中,迫切需要一个高过载值且宽脉冲的加速度来模拟环境,来考核“黑匣子”等关键仪器的工作状态与抗冲击能力,研究其受冲击时的动态响应与可靠性。目前英、美等国家针对飞行记录仪抗冲击需求,研发出了基于炮射方式的冲击试验,来提供宽脉冲、强冲击的冲击环境。根据国际通用ED-112标准,机载事故记录仪需要在幅值3 400g,脉宽6.5 ms的半正弦波冲击环境下检验抗冲击性能,保证飞行数据完整保存,本文中g=9.80 m/s2。因此,对于冲击试验的设计,加速度峰值与脉冲宽度是重要的考量指标。

跌落冲击试验机是常用的冲击试验设备,被测试件可以受到一个近似半正弦的加速度脉冲作用,但产生的峰值加速度量级较小,大致范围为10g～2 000g。马歇特锤通过锤头击打刚性面产生脉冲,调节锤头速度可获得20 000g～30 000g的加速度脉冲幅值,然而脉宽只有十几微秒,主要用于集成电路、加速度计等轻质物体的冲击考核。与马歇特锤相比,Hopkinson杆以压缩空气作为动力源,模拟的过载值更高,可达104g～106g,但持续时间与马歇特锤相当。王文军等[1]以此方法进行了传感器标定与校准研究。以上冲击试验方式能量较低,在轻质试件强度考核中作出了重大贡献,但不能应用于能量较大的子系统、组部件等的工作状态考核。徐鹏等[2]以一级空气炮为载体,研究大能量冲击试验方法,让弹丸撞击加速度存储装置,以毛毡为缓冲获得了高过载的冲击环境,然而此种方法以试件加速的方式获得载荷,并未模拟出运动物体受撞击减速的真实情况,且其脉宽时间只能持续微妙级别。陈刚等[3]也采用空气炮的方式进行冲击试验的研究,以物体减速度的方式受载,虽然试件质量达到了5 kg,获得了20 000g的冲击幅值,然而其冲击脉宽过短,只有1.6 ms。

冲击试验中,缓冲材料的性能直接影响冲击载荷。蜂窝铝是一种良好的轻质缓冲吸能材料,在结构上属于二维多胞材料,具有密度低、压缩应变大、比刚度和比强度高等特性,在动态冲击过程中吸收大量的能量,因而广泛应用于结构减冲击设备。多年来国内外学者深入研究了蜂窝结构受冲击行为。文献[4]中对不同几何结构的金属蜂窝进行了能量吸收和坍塌强度的比较研究。文献[5]中进行了蜂窝的异面冲击试验,研究了材料应变率效应以及空气压缩造成的强度提高效应。孙德强等[6]采用数值计算,以不同速度冲击不同厚跨比和角度的蜂窝进行了平台应力的研究。文献[7]中进行了蜂窝动态压缩试验,在大变形基础下分析了蜂窝剪切和T方向的撕裂。以上研究表明,蜂窝相对密度、胞孔几何构型对其力学性能有重要影响,并且加载方式不同也会影响多胞材料的动态响应。因此,研究蜂窝的相对密度、胞孔构型、冲击速度对蜂窝宏观力学性能的影响对冲击试验设计有重要意义。

为克服冲击试验载荷持续时间过短的缺点,本文以炮射冲击试验为研究对象,数值模拟了试件减速方式的冲击波发生过程,总结了以蜂窝为缓冲材料的相对密度、胞孔构型、冲击速度以及弹丸形状对冲击加速度载荷的影响,剖析了蜂窝变形过程以及动态力学性能,得到相对密度以及弹丸形状对冲击波形的具体作用规律。在此基础上获得了大于3 400g且脉宽接近6.5 ms的冲击载荷,为高过载宽脉冲冲击试验方法提供参考。

1 蜂窝结构异面特性

常用的六边形商业蜂窝铝采用扩展法加工成形,称为双壁厚蜂窝,其蜂窝芯结构如图1所示,x1、x2方向称为面内方向,x3方向称为面外方向,蜂窝胞孔结构可由单壁厚边长l,双壁厚边长h,壁厚δ,双壁厚T,胞孔角度θ(0°<θ<90°)以及孔深b来描述。

相对密度定义为蜂窝铝密度ρ*与基材密度ρs的比值,对于双壁厚蜂窝相对密度ηρ可表示为

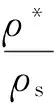
(1)

蜂窝结构异面方向性能通常优于共面方向。x3法向方向上的弹性模量E3与基材模量Es、承载截面面积有关,对于双壁厚六边形蜂窝弹性模量可以表示为

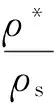
(2)

x3法向方向泊松比ν≈0。

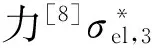
(3)

式中:νs为蜂窝基材泊松比。

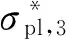
(4)

式中:σys为基体材料的屈服应力。

Wierzbicki[9]通过超叠单元理论得到均匀壁厚六边形蜂窝塑性屈曲应力估算式为

(5)

对于双壁厚正六边形蜂窝,塑性屈曲坍塌应力可以简化为

(6)

2 异面侵彻模型

为分析炮射试验中弹丸侵彻靶板受到的冲击,采用LS-DYNA有限元软件建立了弹丸异面侵彻蜂窝铝有限元模型,如图2所示,将蜂窝铝放置在刚性板前,刚性板为固定约束,忽略弹丸行进中空气阻力的影响,以一定初速向蜂窝铝芯块异面方向侵彻。蜂窝铝块截面为正方形,其边长为2倍弹丸直径,竖直方向胞孔数量大于30个,以避免尺寸效应。蜂窝胞孔为双壁厚等边六边形结构,采用BWC壳单元建模,为保证精度,壳单元厚度方向采用3个积分点,为考虑侵彻过程中的应变率效应以及蜂窝材料失效,采用Johnson-Cook本构模型描述基材,其数据如表1所示。表中:G为剪切模量;A,B,n,C,m为输入常数;Tm为基材熔化温度;Tr为室温,D1～D5为材料失效参数。弹丸采用八节点六面体单元,由于刚度远大于蜂窝铝,采用刚体描述。计算采用基于罚函数法的侵蚀接触算法,弹丸与蜂窝铝之间设置为单面接触以提高计算效率,蜂窝铝之间采用自动接触。为节约计算成本,采用1/2模型进行计算,在对称面施加位移和转角的对称约束。

ρs/(g·cm-1)G/GPaA/MPaB/MPanCm2.78283696840.730.00831.7Tm/KTr/KD1D2D3D4D57752930.1120.1231.50.0070

3 计算结果与分析

为研究弹丸及蜂窝参数对冲击过程的影响,首先选取相对密度为0.077、胞孔角度为30°的等边(正六边形)蜂窝铝作为基准模型进行冲击过程的分析研究,选取质量为4.75 kg的圆头弹丸以138 m/s初速进行冲击。图3为弹丸侵彻蜂窝铝的数值计算结果。可以看出,弹丸侵彻过程中,与弹丸接触的蜂窝孔壁先发生弹性弯曲,随着弹丸进一步运动,轴向应力超过材料的屈服强度,孔壁产生屈曲进而发生塑性坍塌。靠近弹身侧壁的蜂窝胞孔因剪切作用而产生撕裂,除了轴向力作用外,径向力作用将断裂的胞孔推向两侧,产生压缩层。图4为弹丸的冲击加速度a曲线,可以分为3个阶段:上升阶段、中间阶段和下降阶段。上升阶段是弹头侵入阶段,随着接触面积的增大弹丸加速度上升,0.45 ms时刻弹头完全没入蜂窝铝内,加速度达到峰值。在中间阶段,弹丸所受蜂窝反作用力比较稳定,加速度轻微降低。在下降阶段,弹丸速度趋近于0,弹头表面不再挤压蜂窝铝,使加速度迅速降低,弹性压缩得到释放。

为研究蜂窝结构参数对冲击波形的影响,在基础模型上改变相对密度和胞孔角度进行侵彻的数值计算。相对密度取0.058,0.077,0.096,0.115共

4个水平,胞孔角度取15°,30°,45°,60°共4个水平,进行了全参数计算。

图5(a)为弹丸以初速140 m/s侵彻胞孔角度为30°的不同相对密度蜂窝铝的冲击时程曲线,图5(b)为弹丸以初速140 m/s侵彻相对密度为0.077且不同胞孔角度蜂窝铝的冲击时程曲线。由图5可以看出,冲击波形始终为一梯形波,均有明显的3阶段特征,不因为密度和胞孔角度变化而改变基本的形状。图6统计了相对密度和胞孔角度对冲击波形的影响。加速度峰值随相对密度增加而增加,随胞孔角度增加而减小。这表明相对密度增加或在同一密度下减小胞孔角度都可以提高蜂窝铝在异面方向的抗冲击能力。分析认为,在相同胞孔角度下,由式(3)和式(5)可知,相对密度的增大提高了蜂窝铝弹性屈曲应力和塑性坍塌应力，进而使单位面积承载能力提升。由空腔膨胀理论可知,弹丸侵彻过程所受阻力由准静态力和动态力组成,其中准静态力与材料的屈服强度成正比,对于蜂窝铝与它的坍塌应力成正比;动态力与弹丸速度以及靶体密度呈正相关。相对密度的增大最终导致弹丸所受阻力增大,从而使侵彻时的加速度峰值增大,在初始动能相同的情况下,冲击脉宽减小。

由图5(b)可以看到,改变蜂窝胞孔角度对冲击波形的影响与改变相对密度对冲击波形的影响类似。当胞孔角度由0°增加到90°时,蜂窝孔截面从长方形逐渐变为线形,在折角处与坍塌模式相匹配的塑性铰增加量以及孔角处的孔壁延伸量减小,坍塌应力随之减小,蜂窝铝力学性能降低,弹丸侵彻所受阻力减小,加速度峰值减小,冲击脉宽增大。定义相对胞孔角度ηθ=θ/90°,以四阶多项式:

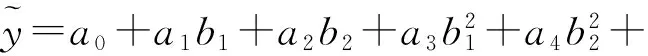
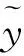
其确定系数R2=0.968,大于0.95,满足精度要求。由拟合结果可知,在中低速侵彻情况下,蜂窝胞孔角度不变时,加速度峰值与相对密度呈线性正相关。当相对密度不变时,加速度峰值为相对胞孔角度的三次函数,即可以用调整相对密度的方式较精确地改变加速度峰值,当靶体质量受限制时,改变胞孔角度以获得所需的冲击加速度峰值。

为研究不同侵彻速度对冲击波形的影响,在基准模型上改变弹丸初速进行数值计算。图7(a)为弹丸冲击速度vi分别为120 m/s,130 m/s,140 m/s,150 m/s,160 m/s时的冲击时程曲线。图7(b)统计了不同弹丸侵彻初速的冲击波加速度峰值和脉宽。由图7(a)可知,速度变化对冲击波形的基本形状影响较小;图7(b)揭示了弹丸速度对加速度峰值和脉宽的影响,弹丸速度从120 m/s升高到160 m/s的过程中,冲击峰值提升了9.4%,脉宽提升了21.9%。由空腔膨胀理论分析得,弹丸所受轴向阻力中的动态阻力与侵彻时的速度平方成正比,速度的提升导致弹丸受到的阻抗升高进而冲击加速度增大。

为研究不同弹丸形状对冲击波形的影响,在基准模型的基础上,分别以相同质量的平头弹、锥形弹(锥角45°)、卵形弹(CRH为2)进行了侵彻计算。图8为不同形状弹头侵彻冲击时程曲线,表2统计了不同形状弹头冲击时程曲线的加速度峰值和脉宽。由图8可以看出,弹头形状对冲击波形有明显的影响。平头弹侵彻时,加速度曲线出现了较大的脉冲,随后迅速回落,表明蜂窝结构的弹塑性屈曲对平头弹侵彻波形作用明显。比较图8中的冲击波形,弹头形状主要影响冲击波上升阶段和下降阶段。在上升阶段,弹丸弹头开始侵入,当弹头完全嵌入靶板时,达到冲击加速度峰值,上升阶段结束。在这一阶段圆头弹、锥形弹、卵形弹母线斜率依次降低,加速度上升速率也依次降低,符合文献[10]弹丸表面所受轴向阻力与弹头母线斜率成正比的规律。在下降阶段,冲击幅值变化速率也受弹头母线斜率影响。卵形弹母线斜率小,其上升和下降阶段较平缓,获得的冲击波形较为平缓。表2展示了弹头形状对加速度峰值和脉宽的影响,平头弹、圆头弹、锥形弹、卵形弹的加速度峰值依次降低,脉宽依次增大,与其他弹头相比,卵形弹侵彻时所受轴向阻力更小。

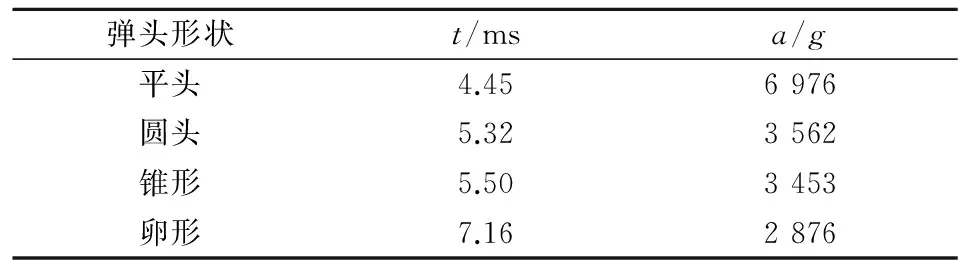
弹头形状t/msa/g平头4.456976圆头5.323562锥形5.503453卵形7.162876

根据蜂窝材料参数和弹丸参数对冲击波形的影响,选择卵形弹,选取相对密度、胞孔构型、冲击速度为设计变量,以脉冲峰值3 400g和脉宽6.5 ms为目标进行了波形设计,流程如图9所示。

设计结果:采用150 m/s的卵形弹冲击胞孔角度为45°、相对密度为0.081 6的蜂窝铝,可以获得目标冲击峰值和脉宽。为验证结果的正确性,将参数代入有限元模型中进行数值计算,结果如图10所示,加速度峰值为3 420g,脉宽为6.44 ms,误差分别为0.59%和0.92%,满足冲击波形设计考量指标。

4 结论

通过对弹丸侵彻蜂窝铝的数值计算与分析,研究了蜂窝材料参数和结构、弹丸冲击速度和弹头形状对冲击波形的影响,并设计获得了满足要求的冲击波形,得到了以下主要结论:

①改变蜂窝铝相对密度和改变胞孔角度都可以改变蜂窝异面力学性能,从而影响冲击加速度峰值和脉宽。其中,提高蜂窝相对密度、减小胞孔角度可以提高加速度峰值。在中低侵彻初速下,冲击峰值近似与相对密度线性正相关,可以通过改变相对密度的方式获得所需的冲击加速度峰值。

②提升冲击初速能够同时提高加速度峰值和脉宽;弹头形状影响冲击波的上升速度和下降速度,决定了冲击波形;弹头母线斜率越小,冲击波形越平缓。

③采用质量4.75 kg、速度150 m/s的卵形弹冲击胞孔角度为45°、相对密度为0.0816的蜂窝铝可以获得符合考量指标的冲击加速度载荷。

由于冲击模型建立在一定假设的基础上,模型具有近似性,本文计算结果有待于试验的进一步验证。

[1] 王文军,胡时胜.高g值加速度传感器的标定[J].爆炸与冲击,2006(6):568-571.

WANG Wen-jun,HU Shi-sheng.Calibration of high shock acceleration sensors[J].Explosion and Shock Waves,2006(6):568-571.(in Chinese)

[2] 徐鹏,祖静,范锦彪.高g值加速度冲击试验技术研究[J].振动与冲击,2011,30(4):241-243.

XU Peng,ZU Jing,FAN Jing-biao.Acceleraton shock test technology with higher values ofg[J].Journal of Vibration and Shock,2011,30(4):241-243.(in Chinese)

[3] 陈刚,胡文军,李思忠,等.高g值宽脉冲冲击实验研究[C]//四川省第二届实验力学学术会议论文集.四川:四川力学学会实验力学专委会,2011:14-23.

CHEN Gang,HU Wen-jun,LI Si-zhong.Acceleraton shock test with higher values ofgand wider pulse width[C]//Proceedings of the Second Academic Conference of Experimental Mechanics in Sichuan.Sichuan:Sichan Society in Mechanics Experimental Mechanics Committee,2011:14-23.(in Chinese)

[4] JEYASINGH V M A.Analytical modeling of metallic honeycomb for energy absorption and validation with FEA[D].Wichita,USA:Wichita State University,2005.

[5] XU S,BEYNON J H,RUAN D,et al.Strength enhancement of aluminium honeycombs caused by entrapped air under dynamic out-of-plane compression[J].International Journal of Impact Engineering,2012,47(4):1-13.

[6] SUN D,ZHANG W,WEI Y.Mean out-of-plane dynamic plateau stresses of hexagonal honeycomb cores under impact loadings[J].Composite Structures,2010,92(11):2 609-2 621.

[7] ZHOU Q,MAYER R R.Characterization of aluminum honeycomb material failure in large deformation compression,shear,and tear-ing[J].Transactions-American Society of Mechanical Engineers Jour-nal of Engineering Materials and Technology,2002,124(4):412-420.

[8] GIBSON L J A A,ASHBY M F.Cellular solids:structure and properties[M].Britain:Cambridge University Press,1998.

[9] WIERZBICKI T.Crushing analysis of metal honeycombs[J].International Journal of Impact Engineering,1983,1(2):157-174.

[10] 蒋志刚,曾首义,周建平.刚性尖头弹侵彻有限厚度金属靶板分析模型[J].兵工学报,2007,28(8):923-929.

JIANG Zhi-gang,ZENG Shou-yi,ZHOU Jian-ping.An analytical model for penetration into finite thickness metallic target struck by rigid sharp-nosed projectiles[J].Acta Armamentarii,2007,28(8):923-929.(in Chinese)

NumericalSimulationonShockWaveformofAluminumHoneycombs

CAO Jie,GE Jian-li,WANG Hao,YANG Guo-lai

(School of Mechanical Engineering,Nanjing University of Science and Technology,Nanjing 210094,China)

In order to analyze the effect of projectile with different structures and aluminum honeycomb target with different material parameters on acceleration response,a nonlinear dynamic finite-element model of projectile penetrating target was established,which was simulated by LS-DYNA software.The influences of different parameters on impulse response were compared including relative density and cell wall angle of aluminum honeycomb,and the initial velocity and the shape of projectile.The results show that the peak acceleration increases,and the pulse width reduces by increasing relative density and reducing cell wall angle.The peak value and the pulse width of the acceleration increase with the increase of initial speed of bullet.The shape of bullet affects the shock waveform,and a smooth acceleration waveform can be obtained by using an oval projectile.The obtained results offer an important reference to selection of parameters in the design of impact experiment with honeycomb aluminum as cushioning material.

aluminum honeycomb;cell configuration;projectile;shock wave;peak value;pulse width;finite element

O39

A

1004-499X(2017)04-0058-06

2017-07-10

国家自然科学基金项目(11572158);国家重大科学仪器设备开发专项(2013YQ470765);中央高校基本科研业务费专项资金资助(30915118825);十三五预研重点项目(30107040705)

曹杰(1993- )男,硕士研究生,研究方向为非线性有限元、冲击试验。E-mail:525508987@qq.com。

葛建立(1980- )男,副教授,博士,研究方向为非线性有限元、虚拟样机、等几何分析研究。E-mail:gejianli@njust.edu.cn。