飞行器可达性问题的统一求解方法研究

乔 浩,李曾浩,李新国,孙 鹏

(西北工业大学 航天学院 陕西省空天飞行器设计重点实验室,陕西 西安 710072)

飞行器可达性问题的统一求解方法研究

乔 浩,李曾浩,李新国,孙 鹏

(西北工业大学 航天学院 陕西省空天飞行器设计重点实验室,陕西 西安 710072)

针对飞行器的可达性问题,研究了可达域与可返回窗口2个子问题。前者着眼于飞行器在现有条件下对地面目标的覆盖范围,后者则更关注于飞行器在返回过程中的空间上界。对描述飞行器可达性问题的2种方法进行深入研究,提出一种统一框架下的飞行器可达性数值求解方法。通过研究与可达域相对应的终端优化问题以及与可返回窗口相对应的初值优化问题,形成了一套完整的求解流程。仿真结果表明,利用所提求解方法能够快速获得飞行器完整的可达性信息,为飞行器的总体设计、任务规划等提供设计参考。

可达性;可返回窗口;逆向优化;再入返回

飞行器的可达性是描述飞行器对于指定目标到达能力的重要手段。现有研究主要包括始于飞行器现有飞行状态的可达域问题,以及始于指定目标的可返回窗口问题。可达域问题已有较多研究,而可返回窗口问题的研究较少。可达域的求解方法主要分为优化方法以及沿最大约束边界飞行方法2种,前者又细分为直接优化方法和间接优化方法。

文献[1]详细介绍了可达域的间接优化方法。文献[2]在此基础上将攻角由程序攻角改为4段参数化攻角,由路径约束决定分段点,对不同方向上的最大航程进行优化,从而获得可达域轮廓。间接法在求解过程中一般以准平衡滑翔条件等假设为基础,与实际动力学模型差距较大,因此仅适用于前期的理论分析,对于高精度求解并不适用。

直接法是一种直接将最优控制问题离散为非线性规划问题进行求解的优化方法。文献[3]采用伪谱法对滑翔式再入飞行器最大航程问题进行了研究,文献[4～5]以此为依据采用加权的经纬度信息进行可达域描述,分别求解了亚轨道飞行器与多脉冲导弹的可达域问题。直接法求解可达域的缺陷在于求解速度较慢,而可达域的出发点在于飞行器的当前状态,无法满足在线计算要求。

文献[6]介绍了一种依据再入走廊沿最大约束边界飞行的可达域快速计算方法。文献[7]在此基础上引入倾侧角反向策略,并对阻力加速度曲线插值方式进行了改进。由于该类方法中攻角与倾侧角相对固定,可达域生成速度较快,但由于引入了较多假设以及经验设计,所生成的可达域并不能完全反映真实情况。

相较于可达域,可返回窗口的研究较少。文献[8]在分析X-38的返回问题时首次提出再入界面窗口概念,在求解过程中利用直接多重打把法进行最大纵程优化。文献[9]将再入界面窗口进一步扩展为再入走廊,通过集合的方法详细给出了可达域、再入窗口界面、三维来路走廊与去路走廊的数学描述方法。由于整个描述过程中引入的来路映射函数与去路映射函数在非线性问题中并不存在,无法以一一对应的形式完成天、地状态之间的映射,因此无法在实际中应用。

本文在总结前人对可达域及可返回窗口研究的基础上,分析二者之间的异同,提出与现有优化问题不同的一类初值优化问题。之后分析了利用伪谱法进行双向优化的可能性,并给出基于该方法的飞行器可达性问题统一数值求解框架,使可返回窗口问题的解算可以脱离在线计算的要求,实现地面的独立规划。通过一系列仿真校验,研究了飞行器可达性问题中可达域、可返回窗口这2个子问题在空间上的相通性。

1 再入问题描述

1.1 动力学模型

再入问题的研究对象一般具有较高的飞行速度,整个再入过程持续时间较短,可忽略地球自转带来的影响。假设地球为非旋转均质圆球,描述飞行器运动状态的变量包括地心距r、经度φ、纬度θ、速度v,以及航迹倾角γ与航向角ψ。其中航迹倾角以当地水平面为参考,速度矢量在上为正;航向角以正北方向为0°参考,速度矢量顺时针旋转为正。飞行器无动力再入三自由运动方程[10]为

(1)

升力加速度aL和阻力加速度aD大小分别为

(2)

式中:ρ为大气密度;S为飞行器参考面积;m为飞行器质量;σ为倾侧角;g为当地引力加速度;CL,CD分别为升、阻力系数,与攻角α有关。

1.2 飞行约束

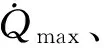
(3)

式中:k为与材料相关的常数;g0为海平面处的引力加速度。

路径约束主要考虑禁飞区、落点位置等的约束。本文在研究中不考虑禁飞区约束,仅对终端速度vf、高度rf加以限制。

控制量取α与σ,其约束为

α∈[αmin,αmax],σ∈[σmin,σmax]

(4)

2 可达性问题求解原理

可达域与可返回窗口是立足于不同出发点的2种可达性描述方法。前者是从飞行器当前状态出发,研究飞行器能够到达的地面范围;后者是从地面的角度出发,探讨飞行器从何处飞来能够符合进场条件并安全着陆。

无论是直接法还是间接法,可达域本质上是一种按照时间过渡、多条边界轨迹的快速规划,并由轨迹末端在地面的投影范围确定出实时能够到达的区域。

相对地,可返回窗口的求解本质上是一种与时间过渡方向相反的轨迹求解,即飞行器的终端位置已知,需要求解其可返回来路在空间的分布区间。如采用间接法或沿最大约束边界飞行方法,求解方向将与时间过渡方向矛盾。

本文在求解过程中采用间接法中较为常用的伪谱法。分析表明,该方法与时间过渡方向无关,是一种全局离散求解的方法。定义初始条件已知,求解终端可达域的问题为终端优化问题;而终端已知,求解初始可返回窗口的问题为初值优化问题。

伪谱法在求解过程中,首先将时域问题转换到[-1,1]区间,之后以N阶Legendre多项式的根作为离散点对状态量、控制量进行离散,离散后状态变量的微分值在相应离散点上与原微分方程组在一定精度上相匹配,从而将微分方程组转化为代数约束。结合状态约束、控制约束以及边界条件构成非线性规划问题。由于非线性规划问题与时间过渡方向无关,只与离散后的各种约束有关,因此伪谱法在理论上可用于初值优化。

由拉格朗日积分可得终端状态X(τf)与初始状态X(τ0)关系如下:

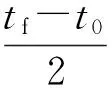
(5)

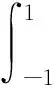
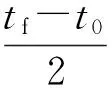
(6)

而对于初值优化问题,此时相当于对初始状态有约束,初始端的状态约束可表示为

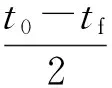
(7)

其表达形式与式(6)一致,可知在离散方式上初始与终端状态的数值约束形式相统一,伪谱法本身具有求解初值优化的能力。

3 基于伪谱法的可达性问题求解框架

可达域问题一般可以描述为不同纵程条件下的横程最大问题,可达域边界点的最大横程可由纬度描述:

J=min{cosθf}

(8)

式中:θf为终端纬度。可达域描述方法如图1所示。

同理,可返回窗口问题可以描述为从终端位置出发,求解不同纵程情况下横程最大问题。飞行器再入返回时初始位置一般在终端位置的一侧,并有一最小距离。采用文献[5]中的坐标系描述方法,规定飞行器初始位置在终端位置西侧,并令终端经、纬度都为0,此时优化目标为

J=min{cosθ0}

(9)

式中:θ0为初始纬度。可返回窗口描述方法如图2所示。

可达域与可返回窗口的统一求解框架如图3所示。

4 仿真校验

本文采用文献[10]所给出的飞行器参数进行仿真校验,分别求取可达域及可返回窗口。

可达域问题与再入过程相对应,其初始点固定,终端点不定。终端约束:hf=24.38 km,vf=762 m/s,γf=-5°;初始条件:h0=79.25 km,经、纬度均为0°,v0=7 802.88 m/s,γ0=-1°。

可返回窗口问题与之相反,其终端点固定,初始点位置不定,因此初始点的待优化信息为初始经纬度。初始条件:h0=79.25 km,v0=7 802.88 m/s,γ0=-1°。为保证可返回窗口位于终端位置的左侧,规定初始最大经度为-20°;终端条件:hf=24.38 km,vf=762 m/s,γf=-5°,ψf=90°,对应经、纬度均为0°。可达域、可返回窗口的三维边界轨迹包络分别如图4、图5所示。

对于飞行器而言,处于可达域或可返回窗口内的轨迹是可行的。可达域与可返回窗口的边界轨迹在空间形成一个区域, 对于确定型号飞行器及相对固定的初始高度、速度,飞行器的可达域及可返回窗口具有唯一性。航向角对比如图6所示。

可见,航向角的过渡过程呈相反趋势,即:可达域问题中,航向角由90°逐渐向增大、减小过渡;可返回窗口问题中,飞行器由不同初始航向角最终过渡至90°,即指向着陆场。其余状态量及攻角、倾侧角对比如图7～图11所示。

图7～图11中,除航向过渡相反外,各变量呈一定的一致性。其原因可归结为:2种描述方式均是由飞行器在空间的最大飞行边界定义,而同一飞行器的边界轨迹反映了飞行器各个方向的最大机动能力,在初始高度、速度(即初始能量)确定的条件下,其在空间中的机动能力随之确定,因此飞行轨迹在空间中具有一定的对应关系。而攻角与倾侧角演变的对应性更进一步反映了对于初始能量确定的问题,初值优化与终端优化具有统一性。由于最大航程问题在初始优化与终端优化中具有典型对应关系,以此为算例对可达性问题的统一解法进行验证,如图12所示。可达域问题初始经、纬度均为0,可返回窗口问题终端经、纬度均为0。

可知,二者轨迹形态相似,飞行器基本沿纵向飞行。所对应的攻角及倾侧角指令如图13所示。

图13中攻角与倾侧角的变化趋于一致,攻角后期基本处于最大升阻比附近;倾侧角基本处于0°附近,仅有10-5量级的微小波动。二者的对应性说明,可达域与可返回窗口这2个不同出发点的问题具有良好的空间对应性,采用本文所提出的统一求解方法,可以方便地获得飞行器完整的可达性描述。

5 结束语

本文在分析可达域与可返回窗口问题关系的基础上,提出了可达性问题统一求解方法,研究表明:

①伪谱法在离散寻优过程中,终端约束与初始约束表示形式一致,反映到算法中即初值优化问题与终端优化问题均可利用该方法进行寻优。

②对于初始能量固定的飞行器,其在空间中的最大机动能力是一定的。而飞行器的机动能力反映了空间中的边界飞行轨迹,当初始位置及航向固定时为可达域问题,不定时为可返回窗口问题。

③数值优化方法求解可达域问题分为问题离散与非线性规划两部分,前者区分了不同的数值优化算法。当采用对寻优方向不敏感的非线性规划算法时,相应的优化方法亦可用于初值优化问题。

[1] LU P,XUE S B.Rapid generation of accurate entry landing footprints[J].Journal of Guidance,Control,and Dynamics,2010,33(3):756-765.

[2] LI H F,ZHANG R,LI Z Y,et al.Footprint problem with angle of attack optimization for high lifting reentry vehicle[J].Chinese Journal of Aeronautics,2012,25(2):243-251.

[3] 丁洪波,蔡洪,张士峰,等.高超声速滑翔式再入飞行器最大航程飞行轨迹分析[J].国防科技大学学报,2009,31(6):67-72.

DING Hong-bo,CAI Hong,ZHANG Shi-feng,et al.The maximum-range trajectory analysis of hypersonic glide-reentry vehicle[J].Journal of National University of Defense Technology,2009,31(6):67-72.(in Chinese)

[4] 解永锋,唐硕.亚轨道飞行器再入可达域快速计算方法[J].飞行力学,2011,29(4):72-75.

XIE Yong-feng,TANG Shuo.Rapid calculation of entry footprint of suborbital launch vehicle[J].Flight Dynamics,2011,29(4):72-75.(in Chinese)

[5] 明超,孙瑞胜,梁卓,等.多脉冲导弹可达域优化方法设计与分析[J].国防科技大学学报,2016,38(1):143-149.

MING Chao,SUN Rui-sheng,LIANG Zhuo,et al.Design and analysis of footprint optimization method for multiple-pulse missile[J].Journal of National University of Defense Technology,2016,38(1):143-149.(in Chinese)

[6] SARAF A,LEAVITT J A,MEASE K D.Landing footprint computation for entry vehicle[C]//Proceedings of AIAA Guidance,Navigation,and Control Conference and Exhibit.Rhode Island:AIAA,2004:1-14.

[7] 常松涛,杨业,王永骥,等.计算再入可达区域的快速算法[J].华中科技大学学报:自然科学版,2012,40(7):1-5.

CHANG Song-tao,YANG Ye,WANG Yong-ji,et al.A rapid algorithm for generating landing footprint for entry vehicles[J].Journal of Huazhong University of Science and Technology:Nature Science,2012,40(7):1-5.(in Chinese)

[8] KINDLER J T,SCHOETTLE U M,WELL K H.Entry interface window of landing site coober pedy for the experimental vehicle X-38 V201:AIAA-2000-4117[R].2000.

[9] 李洪波,余梦伦,肖业伦.升力式再入的三维再入走廊与再入界面窗口[J].宇航学报,2010,31(9):2 059-2 066.

LI Hong-bo,YU Meng-lun,XIAO Ye-lun.Three-dimensional entry flight corridor and entry interface window about lifting reentry[J].Journal of Astronautics,2010,31(9):2 059-2 066.(in Chinese)

[10] BETTS J T.Practical methods for optimal control and estimation using nonlinear programming[M].Philadelphia:SIAM Press,2009.

AUnifiedNumericalMethodforAircraftAccessibilityProblems

QIAO Hao,LI Zeng-hao,LI Xin-guo,SUN Peng

(Shanxi Aerospace Flight Vehicle Design Key Laboratory,College of Astronautics,Northwestern Polytechnical University,Xi’an 710072,China)

Aiming at the reachability problem of vehicle,two sub-problems of footprint and entry interface were studied.The former focused on the coverage of ground targets under the existing conditions,while the latter focused on determining the upper bound during the return process.The methods for describing the reachability problem of aircraft were studied,and a united numerical method for aircraft accessibility was presented.By studying the terminal optimization problem and the initial optimization problem,a complete solution process was formed.Simulation results show that by the proposed method,a complete reachability information for aircraft can be obtained,which provides reference for designing and mission planning of the aircraft.

accessibility;entry interface window;reverse optimization;reentry

V448.2

A

1004-499X(2017)04-0009-06

2017-05-04

乔浩(1989- ),男,博士研究生,研究方向高超声速导弹弹道设计,制导与控制。E-mail:1030483026@qq.com。