基于双谱综合特征提取的距离-速度同步拖引干扰识别方法研究
袁功霖,侯 静,陈 义,张 诚
(1.南京电子技术研究所,江苏 南京 210039; 2.西北工业大学 电子信息学院,陕西 西安 710072;3.上海机电工程研究所,上海 201109)
基于双谱综合特征提取的距离-速度同步拖引干扰识别方法研究
袁功霖1,侯 静2,陈 义3,张 诚3
(1.南京电子技术研究所,江苏 南京 210039; 2.西北工业大学 电子信息学院,陕西 西安 710072;3.上海机电工程研究所,上海 201109)
为有效对抗距离-速度同步拖引(R-VGPO)欺骗干扰,提出了一种综合的双谱特征提取方法用于识别真实目标回波信号和欺骗干扰。建立了拖引干扰信号模型,基于双谱分析良好的抗噪性能,分别对真实回波信号和欺骗干扰作双谱变换。根据双谱估计的结果,用围线积分双谱与辅对角积分双谱提取特征作为一次特征向量;为降低特征维数并消除交叉项干扰,用信息熵和基于Fisher准则的特征选择方法进行二次特征提取,建立特征数适中的综合特征参数集,在保留最具区分度的特征向量的同时,避免信息损失,突出优秀特征值的作用。仿真结果表明:与基于特征选择和基于熵的单一特征提取方法相比,提出的双谱综合特征提取方法可获得更高的识别准确率和更好的抗噪性能,能有效对抗距离-速度同步拖引欺骗干扰。
距离-速度拖引欺骗干扰; 双谱; 围线积分; 对角积分; 特征提取; 特征选择; 信息熵; 支持向量机
0 引言
随着数字射频存储器(DRFM)技术的不断发展,雷达有源欺骗干扰技术获得了广泛应用。DRFM可通过截获、存储、转发敌方雷达信号,瞬时精确模仿雷达波形,在真实目标附近产生时域、频域和空域特征均十分相似的欺骗干扰。这种高逼真度的欺骗干扰可迷惑和扰乱雷达对真实目标的探测和跟踪,甚至造成目标丢失。
目前的欺骗干扰主要分为距离欺骗、速度欺骗、角度欺骗和组合欺骗[1]。其中:距离-速度同步拖引干扰是一种针对多普勒雷达的组合欺骗干扰,能同时对距离和速度信息进行欺骗,是跟踪雷达的一种主要威胁。目前的抗干扰方法主要分为两类:一类是通过设计复杂的发射波形对抗干扰;另一类是通过提取欺骗干扰信号与真实目标回波的特征差异,对欺骗干扰信号进行识别[2-3]。如文献[4-5]通过提取归一化一维小波变换系数谱的能量比参数和频域-慢时域的积谱矩阵的二维分布特征,对欺骗干扰进行了识别。文献[6]用原子分解理论选取合适的过完备字典集进行真假目标特征提取。文献[7]用双谱理论提取特征因子,实现了对不同欺骗干扰方式的识别。但上述研究针对的是单一欺骗方式,未涉及组合欺骗干扰,且在信干比较低时其识别准确率会受到较大影响。
由于高阶统计量固有的抗噪优势,本文选择双谱分析法对信号进行处理。双谱分析方法具平移不变性,并能有效保留信号的幅值和角度信息,理论上可完全抑制高斯噪声及对称分布的非高斯噪声,因此广泛用于信号分类识别[8-10]。但双谱变换导致数据量的急剧增加,需作降维处理,目前较常用的降维方法是对双谱进行积分处理。文献[11]提出了径向积分双谱,积分路径为过双谱平面原点的直线,但该方法损失了信号的幅值信息。文献[12]提出了轴向积分双谱,积分路径为平行于任意频率轴的直线,但该方法损失了部分相位信息。文献[13]提出了围线积分双谱,积分路径为以原点为中心的正方形,具优良的抗高斯噪声性能。文献[14]提出了对角积分双谱,积分路径为平行于对角线的直线,并利用双谱的对称性省略了部分冗余数据点。但单一形式的积分双谱可能不足以描述信号的全部特征,而二维双谱又会导致信息冗余和计算量的增加。针对上述问题,本文提出一种双谱综合特征提取方法对抗距离-速度同步拖引干扰(R-VGPO)。先用矩形围线积分和辅对角积分对双谱阵列作降维处理,再基于Fisher准则进行特征选择,同时结合信息熵完成二次特征提取,进一步降低特征维数,最后通过支持向量机(SVM)完成分类识别。本文方法综合了多种特征提取方法,具特征维数低、识别准确率高等优点。用仿真对该方法在对距离-速度同步拖引这类组合欺骗干扰的识别效果及在低信干比环境中的高识别准确率进行了验证。
1 拖引干扰信号模型
设雷达发射机的脉冲信号以线性调频信号(LFM)表示,则雷达发射信号可表示为
s(t)=A×exp[j2π(f0t+μt2/2)]×
rect(t/τ)
(1)
式中:A为信号幅值;f0为中心频率;τ为一个理想脉冲的持续时间;μ为线性调制斜率;rect(t/τ)为矩形脉冲。则目标回波信号可表示为
sr(t)=Ar×exp[j2π(f0(t-tr)+
μ(t-tr)2/2)]×rect((t-tr)/τ)
(2)
式中:Ar为目标回波幅值;tr为回波延时,且tr=2R0/c;R0为雷达与目标的距离。
当对雷达进行距离-速度联合拖引欺骗时,干扰信号可表示为
Jd(t)=AJ×exp{j2π[f0(t-tr-ΔtJ)+
μ(t-tr-ΔtJ)2/2]}exp(j2πΔfJt)×
rect((t-tr-ΔtJ)/τ)
(3)
式中:AJ为干扰调制幅度;ΔtJ(t),ΔfJ(t)分别为R-VGPO调制的距离时延和多普勒频移。为实现同步干扰,ΔtJ(t),ΔfJ(t)应满足
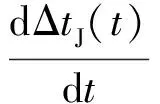
则,当R-VGPO实施匀速拖引时,ΔtJ(t),ΔfJ(t)分别为
(4)
当R-VGPO实施匀加速拖引时,ΔtJ(t),ΔfJ(t)分别为
(5)
式中:t1为拖引开始的时间;v,a分别为拖引的速度及其加速度。
2 双谱域特征提取
鉴于双谱分析法良好的抗噪性能,本文分别对真实回波信号和欺骗干扰作双谱变换,用围线积分法和辅对角线积分法对双谱做一次特征提取;再用Fisher准则和信息熵运算进行二次特征提取,构建特征数适中的综合特征参数集。
2.1 双谱估计
因双谱分析在保留信号幅值与相位信息的同时,还能有效抑制高斯噪声对信号处理的影响,可用于信号的特征表示,故本文对真实信号与欺骗信号进行双谱变换。
设干扰信号的三阶累积量为

Jd(t+τ2)}
(6)
式中:τ1,τ2为滞后时间。对三阶累积量作傅里叶变换,可得干扰信号双谱为
Bd(ω1,ω2)=
(7)
式中:ω1,ω2为频率。
同理可得雷达真实回波信号的双谱。但双谱的精确解析解一般难以获得,需根据有限的数据进行信号的双谱估计。本文用直接法对真实回波信号及欺骗干扰进行双谱估计。
2.2 积分双谱特征
双谱虽较好地保留了信号的幅值与相位信息,但数据量过大,需对其进行特征提取实现降维。同时,双谱虽然理论上可抑制高斯噪声的影响,但实际处理中由于信号序列长度有限,不可能完全抑制高斯噪声,而围线积分双谱在保留信号的尺度信息和部分相位信息的同时,对噪声有较强的抑制效果;辅对角线积分充分利用双谱特殊的对称性对计算进行化简,减少了特征提取的时间。因此,本文采用围线积分和辅对角线积分两种方法进行特征提取[13-14]。
2.2.1 围线积分双谱
假定双谱变换所得为n×n维矩阵,围线积分是沿以原点为中心的正方形进行积分,由内而外,设积分路径为0,1,2,…,L,如图1(a)所示。图1中:每个点代表一个双谱值,该积分方法不会遗漏任一双谱值。
2.2.2 辅对角线积分双谱
辅对角线法的积分路径为在双谱的六边形有效区域内,从左上角开始,沿平行于辅对角线的方向进行积分,直至右下角,如图1(b)所示。该方法的积分结果包含极丰富的信号幅值与相位信息。
2.3 二次特征提取
2.3.1 基于Fisher准则的特征选择
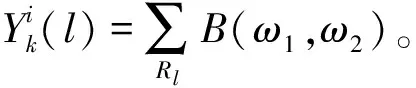
J(l)=(m1-m2)2/(S1+S2)
(8)
式中:l为围线积分所得的数据序号;m1,m2为两类信号的双谱积分均值;S1,S2为两类信号的双谱积分均方误差。此处:
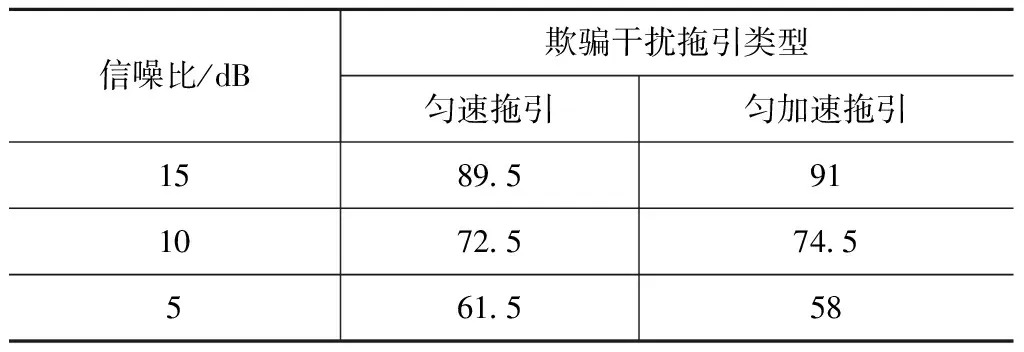
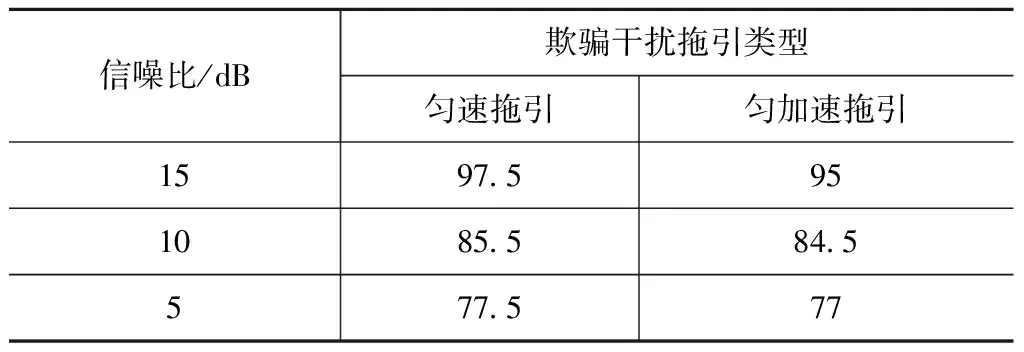
J(l)较大,表明两类目标间具较大的类间可分性和类内聚集性。因此,本文按一定的准则设定阈值Th,当J(l)>Th时,保留对应的积分双谱特征向量;当J(l) 2.3.2 信息熵 熵的概念来自热力学,是表示系统混乱度的物理量。在电子信号领域,可用于衡量信息量的大小。本文用此概念,将二次提取积分双谱的双谱熵和波形熵作为特征向量。 (9) (10) 式(10)可用于计算围线积分双谱及辅对角线积分双谱的波形熵。 信息熵将所有的特征值作相同处理,这会使部分特别有区分度的特征量和无区分度的特征量产生相同的作用,分类能力变差;特征选择算法虽可提取最具区分度的特征值,突出其作用,但摒弃了其余的全部向量,可能造成信息损失。因此,单独采用上述任何一种特征提取方法,都会带来一定程度的性能损失。 为满足高类聚、低耦合和高区分度的分类特征要求,提高识别准确率,本文综合上述两种特征提取方法,在围线积分和辅对角积分双谱组成的统一特征值集合中,利用特征选择算法保留最具区分度的特征向量,并与双谱熵、围线积分均值、围线积分波形熵、对角积分均值、对角积分波形熵共同组成特征参数集,在避免信息损失的同时,突出了优秀特征值的作用,从而实现对欺骗干扰的有效识别。 生成真实目标回波和距离-速度欺骗干扰样本各200个,每类信号随机选择样本100个作为训练集,样本100个作为测试集。设干信比为实际对抗中常见的4 dB[6]。用直接法对生成的样本进行双谱估计,再用不同的特征提取算法进行特征提取,最后用SVM对信号进行分类识别。通过对比不同的特征提取算法的识别率验证本文算法的性能。 在双谱估计的基础上用围线积分或辅对角积分进行一次特征提取,再依据Fisher准则进行特征选择,选取出最具区分度的特征值。设信噪比10 dB,取特征向量1~30个,仿真所得不同特征数下不同特征选择的识别准确率如图2所示。 由图2可知:当特征数较少时,识别的准确率会随特征数增加而明显提高;当特征数达到15后,识别准确率不再明显增长,而是呈平稳波动状态。在匀速拖引欺骗干扰中,辅对角积分双谱的识别效果略好于围线积分双谱,识别准确率会最终稳定于73%左右;在匀加速拖引欺骗干扰中,围线积分双谱的稳定性与准确率都与辅对角积分双谱接近,当特征数足够多时,识别准确率可达约78%。这可能是由于围线积分双谱与辅对角积分双谱分别在抗噪性能与保留信号信息方面各具优势。因此,针对不同类型的信号,识别的效果会略有差异。 在不同的信噪比条件下,针对两种积分方法,分别用特征选择算法选择出特征值15个作为特征向量,识别准确率见表1。 表1 不同信噪比下经特征选择后积分双谱识别准确率 由表1可知:随着信噪比的下降,围线积分与辅对角积分的识别准确率均明显降低;当信噪比较高时,识别结果较好,但当信噪比较低时,识别效果较差,故该方法的抗噪性能较差。 在双谱估计基础上计算双谱熵、围线积分均值、围线积分波形熵、对角积分均值,以及对角积分波形熵,作为5个特征向量,对真假信号进行分类识别。在不同信噪比下针对不同拖引类型的欺骗信号,仿真所得识别准确率见表2。 由表2可知:识别准确率随信噪比减小而降低,识别结果与基于特征选择的特征提取算法中的特征选择方法相近,主要缺点是抗噪性能过差,但该方法的特征值数仅为5个,少于特征选择方法(15个)。 表2 在不同信噪比下基于熵的特征提取算法的识别准确率 本文提出的综合特征提取算法将双谱熵、围线积分均值、围线积分波形熵、对角积分均值、对角积分波形熵予以保留,在此基础上添加经特征选择算法所选择的积分双谱。因围线积分有较好的抗噪性能,而辅对角积分又可较好地保留信号的幅值与相位信息,故综合算法将两种积分方法获得的初步特征向量组合,基于Fisher准则从中选择最具区分度的特征值10个(实验表明7个来自围线积分双谱,3个来自对角积分双谱),共计特征值15个,与基于特征选择的特征提取算法中特征选择方法的特征值数保持一致。仿真所得不同信噪比下本文算法的识别准确率见表3。 表3 综合特征提取算法在不同信噪比下的识别准确率 比较表1~3可知:在三种信噪比下,本文的综合特征提取算法的识别准确率均明显高于其他单一提取方法,且抗噪性能更好,即使在低信噪比条件下,也能保证识别准确率约80%。 SVM的分类识别准确率会受多种因素的影响。由表1~3可知:信噪比会对实验结果产生较大的影响,各种算法的识别准确率都会随信噪比增大而提高;特征选择的数据量也会对结果产生影响,由图1可发现当特征数不足15时,随着数量的减少,识别准确率会降低,而选取15个特征值不仅可获得较好的识别效果,而且不会导致分类器的计算复杂度过高,故其他算法的特征值数量也控制为15;特征选择方法亦会对实验结果产生影响。实验发现,与传统方法相比,本文提出的综合特征提取算法的识别效果有明显优势。 综合特征特征提取算法在运算量没有明显增加的前提下,提高了针对欺骗干扰的识别准确率,并提升了抗噪性能。但该算法目前只适于距离-速度同步拖引欺骗干扰,针对其他类型欺骗干扰方式的识别还有待进一步研究。 针对距离-速度同步拖引欺骗干扰,本文研究了基于双谱变换的特征提取算法。分析了面向整体的熵运算提取算法和面向单个特征值的特征选择算法,提出了保持上述两种方法优点的综合特征提取算法,并比较了不同欺骗类型、不同信噪比下的识别准确率。仿真结果表明:本文提出的综合提取算法在对距离-速度同步拖引这类组合欺骗干扰的识别中具有良好效果且在信干比低的环境中仍能保持较高的识别准确率,抗噪性能强,可有效对抗距离-速度同步拖引欺骗干扰。 [1] 赵国庆. 雷达对抗原理[M]. 西安: 西安电子科技大学出版社, 1999. [2] 单凉, 张剑云, 周青松, 等. 基于拟合优度的欺骗干扰识别方法[J]. 探测与控制学报, 2016, 38(2): 98-102. [3] AKHTAR J. Orthogonal block coded ECCM schemes against repeat radar jammers[J]. IEEE Transactions on Aerospace and Electronic Systems, 2009, 45(3): 1218-1226. [4] 田晓, 唐斌. 基于归一化小波分解能量比的雷达有源欺骗干扰识别[J]. 数据采集与处理, 2013, 28(4): 416-420. [5] TIAN X, TANG B, GUI G. Product spectrum matrix feature extraction and recognition of radar deception jamming[J]. International Journal of Electronics, 2013, 100(12): 1621-1629. [6] 孙闽红, 唐斌. 基于原子分解理论的雷达欺骗式干扰信号特征提取[J]. 电波科学学报, 2008, 23(3): 550-554. [7] 李建勋, 唐斌, 吕强. 双谱特征提取在欺骗式干扰方式识别中的应用[J]. 电子科技大学学报, 2009, 38(3): 329-332. [8] CHITTORA A, PATIL H A. Classification of normal and pathological infant cries using bispectrum features[C]// 2015 23rd European Signal Processing Conference (EUSIPCO). Nice: [s. n.], 2015: 639-643. [9] SHAHID S, SINHA R K, PRASAD G. A bispectrum approach to feature extraction for a motor imagery based brain-computer interfacing system[C]// 2010 18th European Signal Processing Conference. Aalborg: [s. n.], 2010: 1831-1835. [10] LAING K, HUANG Z, HU D, et al. An individual emitter recognition method combining bispectrum with wavelet entropy[C]// 2015 IEEE International Conference on Progress in Informatics and Computing (PIC). Nanjing: IEEE, 2015: 206-210. [11] CHANDRAN V, ELGAR S L. Pattern recognition using invariants defined from higher order spectra: one dimensional inputs[J]. IEEE Trans on S P, 1993, 41(1): 205-212. [12] TUGNAIT J K. Detection of non-Gaussian signals using integrated polyspectrum[J]. IEEE Trans on S P, 1994, 42(12): 3137-3149. [13] 陈韬伟, 金炜东, 李杰. 基于围线积分双谱的雷达辐射源信号个体特征提取[J]. 计算机工程与应用, 2013, 49(8): 209-212+252. [14] 肖乐群, 张玉灵, 赵拥军. 基于对角积分双谱的雷达辐射源信号识别[J]. 信息工程大学学报, 2012, 13(1): 95-99. [15] 周绍磊, 廖剑, 史贤俊. 基于Fisher准则和最大熵原理的SVM核参数选择方法[J]. 控制与决策, 2014, 29(11): 1991-1996. IdentificationofRange-VelocityGatePullOffJammingBasedonIntegratedFeatureExtractionofBispectrum YUAN Gong-lin1, HOU Jing2, CHEN Yi3, ZHANG Cheng3 (1. Nanjing Research Institute of Electronics Technology, Nanjing 200139, Jiangsu, China;2. College of Electronic and Information, Northwestern Polytechnical University, Xi’an 710072, Shaanxi, China;3. Shanghai Institute of Electromechanical Engineering, Shanghai 201109, China) In order to counteract range-velocity gate pull off deception jamming effectively, the integrated bispectrum extraction method was put forward to identify real echo and deception jamming. The pull off jamming model was established. Based on the good anti-noise performance of bispectrum estimation, the initial eigenvector was extracted by surrounding-line integral bispectrum and secondary diagonally integral bispectrum. To reduce feature dimension and eliminate the cross disturbance, the second feature was extracted by information entropy and feature selection based on Fisher criterion. The integrated feature set with suitable feature number was obtained, which could avoid the information loss while keeping the feature vector with the most distinguish degree. So the excellence features were emphasized. The simulation results show that the proposed integrated bispectrum feature extraction method can obtain higher identification accuracy and counteract range-velocity gate pull off deceptive jamming effectively compared to a single feature extraction based on feature selection or entropy. range-velocity-gate-pull-off (R-VGPO) deception jamming; bispectrum; surrounding-line integral; diagonally integral; feature extraction; feature selection; information entropy; support vector machine 2017-05-25; 2017-07-10 航空科学基金资助(2016ZC53033);上海航天科技创新基金资助(SAST2015011) 袁功霖(1993—),男,硕士生,主要研究方向为雷达信号处理等。 1006-1630(2017)06-0109-06 TN974 A 10.19328/j.cnki.1006-1630.2017.06.017

2.4 综合特征参数集构建
3 仿真实验与结果
3.1 基于特征选择的特征提取算法仿真验证
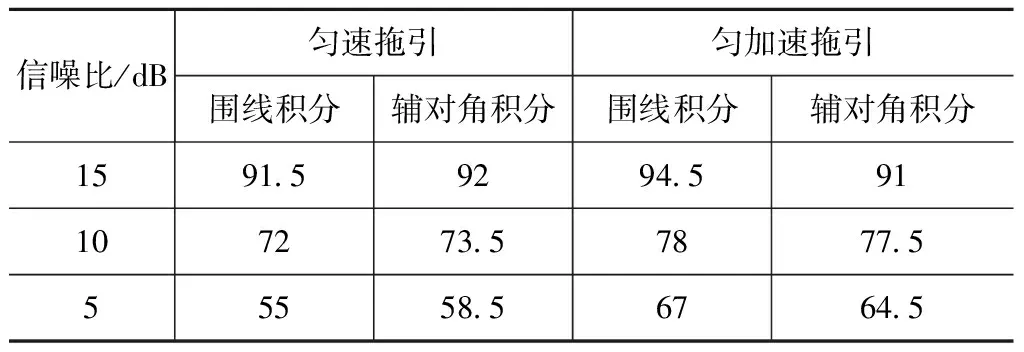
3.2 基于熵的特征提取算法仿真验证
3.3 综合特征提取算法仿真验证
3.4 仿真结果分析与讨论
4 结束语

