单透镜望远镜及其成像参数的研究
潘开欣 刘怡然 潘志民
(南京外国语学校,江苏 南京 210008)
单透镜望远镜及其成像参数的研究
潘开欣 刘怡然 潘志民
(南京外国语学校,江苏 南京 210008)
本文为作者在研究第30届国际青年物理学家竞赛(IYPT2017)第3题的基础上形成,按题目要求设计用小孔光阑替代目镜,自制出简易单透镜望远镜。根据几何光学和波动光学相关理论,作者比较全面地探讨了孔径和透镜焦距等装置参数对单透镜望远镜成像放大率、清晰度和亮度等成像参数的影响。在此基础上作者通过实验对这些参数进行定量研究,借助于Matlab、ToupView等计算机软件对实验数据进行了详细的分析。本文发现理论和实验具有良好的自洽性,从而得到了一般性结论。文末对研究中可能导致误差的因素进行了分析,并对不足之处进行了展望。
小孔成像;单透镜望远镜;放大率;分辨率;对比度;亮度
自1608年荷兰人汉斯·利伯希制作出第一架望远镜以来,望远镜一直被应用于人们的生活观察和学术研究。对于一般的望远镜,多是由双透镜甚至更多透镜组成。本文提出一种用小孔成像代替目镜成像的方案,建立了简单的光学模型,自制出由一个透镜组成的的单透镜望远镜,并对其性能加以研究。
1 单透镜望远镜的理论研究
1.1 普通望远镜与单透镜望远镜

图 1 (a) 用开普勒望远镜观察非无穷远物体; (b) 单透镜望远镜基本光路
在日常生活中,开普勒望远镜是最经常使用也是最广为人知的。如图1(a)所示,它由两块凸透镜组成,远处的物体首先经物镜Lo在近处成一倒立的中间实像S1,目镜Le的作用则相当于放大镜,中间像经它折射后最终成一放大的倒立虚像S2。
在单透镜望远镜中,如图1(b)所示,我们使用一个小孔A代替目镜,借助小孔成像的原理对中间像进行放大。严格说来,小孔成像并没有“成像”,只是通过几何关系实现“放大”功能。除此之外,小孔的大小决定了物平面上一点发出的光束通过时的孔径,从而影响成像的清晰程度。
对于一个观察远处物体的望远系统,常见的参数指标包括图像放大率、分辨率、对比度和照度(亮度)等。下面,我们将逐一讨论这些参数的相关理论与实验。
1.2 视角放大率
望远镜所要观察的物体一般离望远镜本身有一定的距离。在通常情况下可以近似认为物体在无穷远处,中间像近似成在物镜的焦平面上。当观察远处的物体时我们常用视角放大率来表征望远镜的放大功能。视角放大率M定义为最后成的像对人眼(瞳孔)的张角ω′与物体在实际位置对人眼所张视角ω的比值,即:
M=ω′/ω
(1)

图 2
如图2所示,在单透镜望远镜中假定光线傍轴条件近似成立,并假设物体到物镜的距离u远大于物镜焦距f,人眼靠近屏幕观察。我们可以导出单透镜望远镜视角放大率为

(2)
式中,s、t分别为小孔成像的“物距”与“像距”;s0为光屏P到观察者的距离。
由此可知,单透镜望远镜的视角放大率与小孔位置密切相关,并与物镜焦距呈正相关。
1.3 分辨率
1.3.1 几何光学理论
小孔的尺度会导致物平面上的点在像平面成像时产生模糊。当像平面两个光斑之间恰好没有重叠(即恰好相切)时,可以视为能够分辨。若物平面上相距δH的两个点,在单透镜望远镜的像平面上成的光斑恰好没有交叠,则从几何光学可以导出(过程略)

(3)
式中d为小孔直径,其余参量如图2所示。
据此可以得出,单透镜望远镜可以分辨的最小距离δH与小孔直径d呈正比,与小孔到屏幕距离t呈负相关关系。
1.3.2 衍射理论
实际上,在小孔尺寸较小时,需要考虑光的衍射带来的影响。设小孔直径为d,透镜直径为D,其他参数如图2所示。
首先我们考虑物镜(透镜)衍射的影响。因为u≫v,可以近似为平行光入射。由夫琅禾费衍射的相关结论,可得透镜衍射导致的最小分辨距离为

(4)
代入实验参数:D=50mm,u≈5m,波长λ取550nm,可估算出δH≈0.1mm。故我们可以忽略透镜衍射对分辨率的影响。


(5)
作出最小分辨距离δH与小孔直径d关系的趋势示意图如图3所示。从图中我们可以看到:当孔径较大的时候,几何光学对分辨率的影响占主要地位;当孔径较小的时候,主要的限制因素则为衍射。可知当小孔直径取适当值时,该望远镜的分辨能力最强。图中的“总体效果”综合两种因素定性地反映出总体变化趋势,其具体函数关系可由小孔菲涅尔衍射推导。

图 3

图 4
如图4所示,“点光源”Q发出的球面波在小孔所在平面A的复振幅可以写为
(6)

(7)

(8)
而P点的光强为
(9)
我们很难给出这个积分的解析表达式,故转而使用计算机数值模拟的手段,画出光强分布的函数图像,如图5(a)所示。该图展示的是一组实验典型数值:s=50mm,t=250mm,d=500μm的模拟结果,波长取为550nm,透镜焦距取200mm。

图 5 (a) 典型数值下的屏上光强分布; (b) 最小分辨距离随小孔直径变化的理论图线
按照惯例,我们将峰的半高全宽对应物平面上的距离作为最小分辨距离。然而,对于菲涅尔衍射,某些情况下光斑中心为暗区或有复杂的光强起伏,为“恰好能够分辨”的确定造成了一定的困难。例如,对于图5(a)中的情况,我们取外侧峰高度一半的位置作为参考计算最小分辨距离。由此,保持s=50mm,t=250mm不变,画出最小分辨距离δH随小孔孔径d的变化曲线如图5(b)所示。当然,这样的处理在某些情况下可能引起一定的偏差。
可以看到,图线总的趋势与之前的理论推导(近似)相符。曲线在特定的位置出现极小值,对应分辨最为清楚时的小孔直径。
1.4 对比度
当观察一个间隔透光的栅栏状分辨率板(如图6)时,成像黑白区域之间的深浅差别被称为对比度,或称衬比度。实际测试中,我们使用公式

(10)

图 6
表示图片的对比度。式中ILight为分辨率板透光区域的光强计数值,Idark为分辨率板不透光区域的光强计数值。理想情况下对比度为1,如果明暗条纹完全不能分辨,则对比度为零。通常图像的对比度需要达到0.4以上人眼才能够清晰分辨。
无论是图像的对比度还是分辨率,均反映了单透镜望远镜成像的清晰程度。
1.5 亮度
亮度往往指的是光源的亮度,而这里所考虑的亮度实际上是像面的光照强度,简称照度。其定义为单位面积上所接受可见光的能量,用于指示光照的强弱和物体表面被照明的程度。设面元dS上的光通量为dФ,则此面元上的照度E为
E=dΦ/dS
(11)
显然小孔越大通过的光就越多,即成像面上的照度与小孔尺寸成正相关关系。
2 单透镜望远镜实验研究
2.1 实验器材和参数
直径为25mm,焦距为100mm,125mm,150mm,175mm,200mm的凸透镜
直径为50mm,焦距为200mm的凸透镜
直径为50μm, 100μm,200μm, 500μm定径小孔和800μm以上变径小孔
CMOS照相系统(包含CMOS相机,0.6倍远心镜头)
被观测物体: 白炽灯,黑胶带(可裁剪),分辨率板(自加工)
毛玻璃(用作光屏)
配件: 光学平台、元件支架、实验手套等
2.2 实验过程与内容
如图7(a)所示,将CMOS照相系统,毛玻璃屏,针孔和透镜根据理论光路组装,调节各元件共轴等高,并对准用作物体的分辨率板(如图7(b)所示)。仔细调整小孔与照相系统的前后位置,使得通过CMOS照相系统可以清晰观察毛玻璃屏上的图像并将其呈现在电脑屏幕上,如图7(c)所示。我们先后改变了小孔到屏幕距离t、小孔直径d、透镜直径D,透镜的焦距f等参数,对每次实验获得的图像截图,再利用Matlab、ToupView等计算机软件对图像的各项参数作进一步分析。

图 7
远心镜头在使用时,图像上的像素距离与实际距离的比为一个已知的定值。通过软件我们可以测量图片上任意两点的距离,利用镜头的放大倍数和CMOS相机芯片像素的尺寸计算出图像中条纹之间的实际间距(像的大小H2),从而可以与分辨率板相比较,计算出望远镜实际的放大率M的值。
接着将图片输入Matlab,提取图像中心一列像素的光强计数值,呈现其明暗趋势,如图8所示。在图中读取相邻峰谷的差值,并除以峰谷数据的平均值,根据公式(10)计算其对比度。

图 8
在每次实验中,我们选取图像中的一小块区域,利用ToupView自动调节相机的曝光时间和增益,使其灰度保持在一个定值。由此我们可以用曝光时间与增益乘积的倒数衡量亮度的相对大小。
2.3 实验数据研究分析
实验过程中,固定透镜与屏的距离为300mm,物体(分辨率板)距望远镜约4.8m。
2.3.1 放大率M与小孔到屏幕距离t以及透镜焦距f的关系
在研究放大率M随小孔到屏幕距离t关系的实验中,我们使用直径为50mm,焦距为200mm的透镜,小孔直径100μm。根据实验数据,作出放大率M随小孔到屏幕距离t关系如图9(a)所示。
在研究放大率M随透镜焦距f的关系的实验中,我们分别选用焦距为100mm、125mm、150mm、175mm、200mm的透镜,直径为100μm的小孔,设置小孔到屏幕的距离为67mm。根据实验数据,作出放大率M随小孔到屏幕距离t关系如图9(b)所示。
通过实验发现,单透镜望远镜的视角放大率与小孔到屏幕距离呈正相关关系,与透镜焦距呈正相关关系,与之前的理论预测相符。
2.3.2 清晰度与小孔到屏幕距离t以及小孔直径d的关系
在研究对比度φ随小孔到屏幕距离t关系的实验中,我们使用直径为50mm,焦距为200mm的透镜,小孔直径100μm。测出分辨率板透光区域和不透光区域的光强计数值,代入公式(10)计算出对比度φ,作出对比度φ随小孔到屏幕距离t关系如图10(a)所示。
在研究对比度φ随小孔直径d的关系的实验中,我们使用直径为50mm,焦距为200mm的透镜,设置小孔到屏幕的距离为67mm,分别选用直径为50μm、100μm、200μm、500μm的小孔,根据实验数据,作出对比度φ随小孔直径d的关系如图10(b)所示。

图 9 (a) 放大率M与小孔到屏幕距离t关系; (b) 放大率M随透镜焦距f的关系

图 10 (a) 对比度φ与小孔到屏幕距离t关系; (b) 对比度φ与小孔直径d的关系
在研究最小分辨距离δH随小孔直径d的变化的实验中,我们用自行加工的不同间距的栅栏状铝板作为简易的分辨率板(如图11(a)所示),大致测定了单透镜望远镜的分辨能力。实验结果与理论值的比较如图11(b)所示。由于加工能力的限制,我们仅使用了整数毫米间距的分辨率板,而无法得到最小分辨间隔δH更为精确的值。图中每个实验值竖线上端表示能够分辨的最细板子的间距,下端表示不能够分辨的最粗板子的间距,实际的准确值在二者之间。从图中可以看出,实验与理论值的变化趋势吻合的很好。在小孔较大时,望远镜的实际分辨能力低于预期,这可能是理论中判断“恰好分辨”的判据不够准确造成的。

图 11 (a) 自行加工的分辨率板; (b) 最小分辨距离δH与小孔直径d的关系
对比度和分辨率(最小分辨距离)都反映了单孔望远镜成像的清晰程度。通过实验发现:单孔望远镜成像的清晰程度与小孔距屏幕距离呈正相关关系;小孔的直径过大或过小,单孔望远镜的成像均不清晰。这一结论对望远镜性能的改进有重要的指导意义,如小孔的选择。
2.3.3 亮度与小孔直径d以及小孔到屏幕距离t的关系
在研究成像亮度与小孔直径d关系的实验中,我们使用直径为50mm,焦距为200mm的透镜,设置小孔到屏幕的距离为67mm,灰度值为200,分别选用直径50、100、200、500μm的小孔, 作出相对亮度B与小孔直径d的关系如图12(a)所示。

图 12 (a) 相对亮度B与小孔直径d的关系; (b) 相对亮度B与小孔到屏幕距离t的关系
在研究亮度与小孔到屏幕距离t关系的实验中,我们使用直径为50mm,焦距为200mm的透镜,选用100μm小孔,设置灰度值为150, 作出相对亮度B与小孔到屏幕距离t的关系如图12(b)所示。
通过实验发现,单透镜望远镜成像的亮度与小孔到屏幕距离呈负相关关系,亮度与小孔直径呈正相关,与理论预测一致。
3 误差分析
3.1 理论研究过程中存在的误差
在理论推演过程运用光的傍轴近似;使用程序模拟确定最小分辨距离时,因计算精度与判断恰能分辨不准确导致的误差。
3.2 实验研究过程中存在的误差
实验中光路调节引起的误差;各长度量(如小孔到屏幕的距离等)测量的误差;即使在黑暗环境中实验,仍可能由于墙壁或杂散光产生噪声信号导致误差;图像分析时由于图像清晰度有限,像素点选取与测量有误差;尽管实验中使用高质量的粘合消色差透镜,但实际上透镜的色差与像差依然存在。
4 结论及展望
4.1 结论
本文提出一种用小孔成像代替目镜成像的方案,建立了简单的光学模型,自制出简易的单透镜望远镜。通过理论分析和实验研究发现了单透镜望远镜成像放大率、清晰度和亮度等成像参数与孔径和焦距等透镜参数的关系,并且理论与实验有着较好的自洽性。
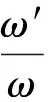
在实验研究层面,我们发现该望远镜放大率与小孔到屏幕的距离的数据,与理论公式(2)符合
得较好,且放大率与透镜焦距呈正相关关系;对比度和分辨率(最小分辨距离)都能反映成像的清晰程度,实验表明该望远镜成像的清晰度和小孔距屏幕距离呈正相关关系,且小孔的直径过大或过小,该望远镜的成像均不清晰;该望远镜成像的亮度与小孔到屏幕距离呈负相关关系,与小孔直径呈正相关,这与理论分析一致。
4.2 展望
突破实验仪器限制,下一步可以利用更多直径及焦距的透镜,以及更多直径的小孔进行大量的实验研究。少受机械加工能力的限制,更精细的测量将考虑用专业的分辨率板进行更精细的研究。多次测量实验,减少不必要的人为操作误差,以提高实验的精准度。进一步从理论和实验定量研究关于清晰度、亮度与相关参数的关系。考虑除放大率,分辨率以及亮度,对比度以外,进一步研究更多参量对望远镜成像性能的影响。
5 结语
在本文中,我们从几何光学和波动光学全面地入手,搭建了一架单透镜望远镜,定量地分析了各个参量对其放大率、清晰度、亮度的影响,经过实验的进一步验证,发现了理论和实验具有良好的自洽性,从而得到了一般的结论并对研究中的误差进行分析,不足之处进行了展望。希望我们研究能给中学生朋友们从事研究性学习提供一些帮助和思考,希望得到更多的批评与指正。
最后在此感谢南京迈塔光电Metalab创新实验室提供实验装置和场地,感谢蒋尚池博士提供宝贵意见。
[1] Young M. Pinhole Optics[J]. Applied Optics, 1971, 10(12): 2763-2767.
[2] Young M. The pinhole camera: Imaging without lenses or mirrors[J]. Physics Teacher, 1989, 27(27): 648-655.
[3] 张三慧.大学物理学.热学、光学、量子物理[M].3版.北京:清华大学出版社,2009:209-294.
[4] 钟锡华.现代光学基础[M].北京:北京大学出版社,2012:61-76.
RESEARCHONTHESINGLE-LENSTELESCOPEANDITSIMAGINGPARAMETERS
PANKaixinLIUYiranPANZhimin
(Nanjing Foreign Language School, Nanjing Jiangsu 210008)
In this paper, we have designed a simple single-lens telescope based on the problem No.3 in International Young Physicist Tournament (IYPT2017). According to theories of geometric optics and physical optics, we systematically explored the influences of aperture and focal length on the magnification of the telescope, the contrast and brightness of the image and so on. We have experimentally conducted quantitative studies by varying these parameters and elaborated analysis of data with software including Matlab and ToupView. As the experimental results are consistent with our theory, a generic conclusion has been drawn. Besides, possible origination of errors in the studies has been discussed and an outlook has been proposed.
pinhole imaging; single lens telescope; magnification; resolution; contrast; brightness
2017-06-18;
2017-08-02
潘开欣,女,高中在读,1372716936@qq.com;刘怡然,男,高中在读,yysflyr@126.com;潘志民,男,中学高级教师,主要从事高中物理教学和竞赛工作,研究方向是中学物理教育,njwxpzm@139.com。
潘开欣,刘怡然,潘志民. 单透镜望远镜及其成像参数的研究[J]. 物理与工程,2017,27(6):116-122.
■

