自动驾驶车辆LQR轨迹跟踪控制器设计

（湖北汽车工业学院，湖北 十堰 442002）

自动驾驶车辆LQR轨迹跟踪控制器设计

陶冰冰，周海鹰，王思山

（湖北汽车工业学院，湖北 十堰 442002）

为了提高智能车的控制精度，以碰撞中心（Center of Percussion，COP）为参考点建立前馈-反馈控制模型，并用该控制模型求解LQR（Linear Quadratic Regulator）问题，获得状态反馈控制率，实现最优控制。在双移线工况和8字形工况下，使用Matlab/Simulink和Carsim对LQR轨迹跟踪控制器进行联合仿真。结果表明：与固定增益前馈-反馈控制器相比，LQR轨迹跟踪控制器的控制精度更高。

自动驾驶；轨迹跟踪；LQR控制器；Carsim/Matlab仿真

人均汽车占有量的不断上升引发了例如车辆拥堵、交通事故、环境污染、能源消耗等一系列问题，其中交通事故尤为突出。自动驾驶智能车的出现为解决交通事故的发生提供了一种新的解决办法。高精度的轨迹跟踪控制器是实现自动驾驶车辆安全稳定行驶的前提，也是智能车实现智能化、商用化的必要条件［1］。目前主要采用的轨迹跟踪控制方法有PID（Proportion Integration Differentia⁃tion）控制、前馈-反馈控制、线性二次型调节器LQR跟踪控制［2］。PID控制器是一种在工程上广泛应用的线性控制器，其优点是无需建立系统模型，控制参数可通过试凑法得出；其缺点是试凑控制参数耗时，需大量试验工作［3］。前馈-反馈跟踪控制［4-5］是近年来采用较多的一类跟踪控制方法，前馈控制主要进行参考路径曲率变化的干扰量补偿，反馈控制主要根据车辆状态反馈调整控制输入使得扰动和模型误差对跟踪的影响最小化，使车辆保持稳定。但该方法在高速情况下误差会不断放大，无法跟踪弯曲道路［6］。LQR控制器通过将非线性控制系统简化成线性控制系统，并对该系统通过求解LQR问题获得状态反馈控制率，实现轨迹跟踪［7-8］，LQR控制器适合于高速公路上的无人驾驶和大部分城市场景下的路径跟踪［7］。文中在二轮自行车模型的基础上，以COP［9］为参考点建立控制模型，并结合LQR算法设计LQR轨迹跟踪控制器，最后分别针对双移线与8字形2个典型工况进行仿真，对设计的轨迹跟踪控制器进行效果验证。

1 LQR控制器设计

1.1 前馈控制器设计

为了消除道路曲率变化对智能车轨迹跟踪精度的影响，采用前馈控制器在干扰曲率作用的瞬间进行抵消。要实现预期跟踪控制效果，需对被控系统的动力学特性和外部扰动特征进行建模。文中以COP为参考点设计控制模型，以消除与后轮侧偏力相关的影响因素，此方法产生的前馈转向控制命令对后轮侧偏力的干扰有很强的鲁棒性，也简化了控制器结构的设计。二轮自行车模型［4］见图1：a为前轴距，b为后轴距；Fyf为前轮侧偏力，Fyr为后轮侧偏力；ψ为汽车头指向，ψr为道路指向；Δψ为头指向误差；xp为投影距离常量；e为横向偏差。

图1 二轮自行车模型

假设只有小的偏转角并忽略纵向力，二轮自行车动力学模型以及轨迹跟踪状态变量为

式中：ay为横向加速；Uy为横向速度；Ux为纵向速度；r为横摆角速度；m为小车质量；Izz为车辆的偏航惯性矩。

以轨迹跟踪能力为目的，车辆的动态状态变量Uy与r需要转变为与期望路径相关的状态变量。结合式（1）～（2）对式（3）～（4）进行微分得到：

式中：k为曲率；s为运动距离。

在已知车轮侧偏力与车轮侧偏角以及车轮侧偏角与方向盘转角关系的前提下，前轮驱动汽车通过转向执行机构控制Fyf，但不能直接控制Fyr，Fyr产生于前驱汽车车体运动引起的后轮侧偏角αr，与汽车转弯时的离心力平衡，因此Fyr会随汽车的动态性还有在极限情况下的非线性而不断改变。选择适当的参考距离xCOP使Fyr的影响被忽略，同时避免计算Fyr，此参考点被称为COP。

对式（7）变形得到：

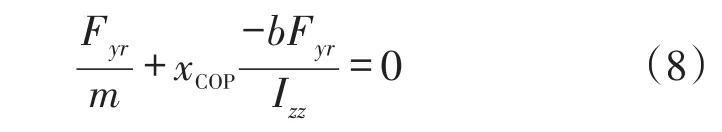
将式（8）代入式（6）中：

式中：eCOP为以COP为参考点的横向误差；L为车长，L=a+b。

从式（9）中可以看出：eCOP仅仅依赖Fyf，Fyf可以直接通过转向输入控制。为了消除道路曲率的影响，将式（9）中的取零，得到Fyf如式（10）所示，此时Fyf称为前轮前馈侧偏力。

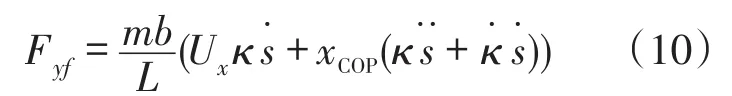
1.2 反馈控制器设计

外部环境的干扰和模型的不准确性，导致智能车在实际运行中会出现寻迹误差。为了消除误差、提高轨迹跟踪控制精度，文中通过增加Fyf的反馈改进策略来消除误差。

将式（11）代入式（5）和式（9）得到：

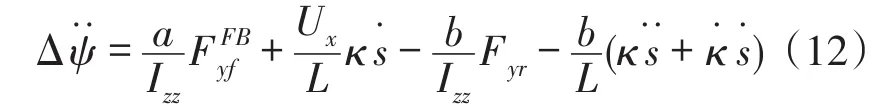
式（12）中有后轮侧偏力的影响，后轮侧偏力由汽车动态运动而产生，是后轮侧偏角αr的函数。为了提高模型准确性，采用非线性轮胎模型。轮胎力与轨迹状态变量关系可以描述为

式中：COP近似等于L，由于Izz能够近似为mab(Izz≈mab)，意味着xCOP≈a。将式（14）代入式（12），即可消除Fyr对 Δ的影响。将上述模型转变为状态空间形式，通过对式（15）采用最优线性二次型调节器LQR求得反馈增益K=[k1k2k3k4]，再基于车辆的实时状态便得到消除误差影响的前轮侧偏力，此时得到的前轮侧偏力称为前轮反馈侧偏力。

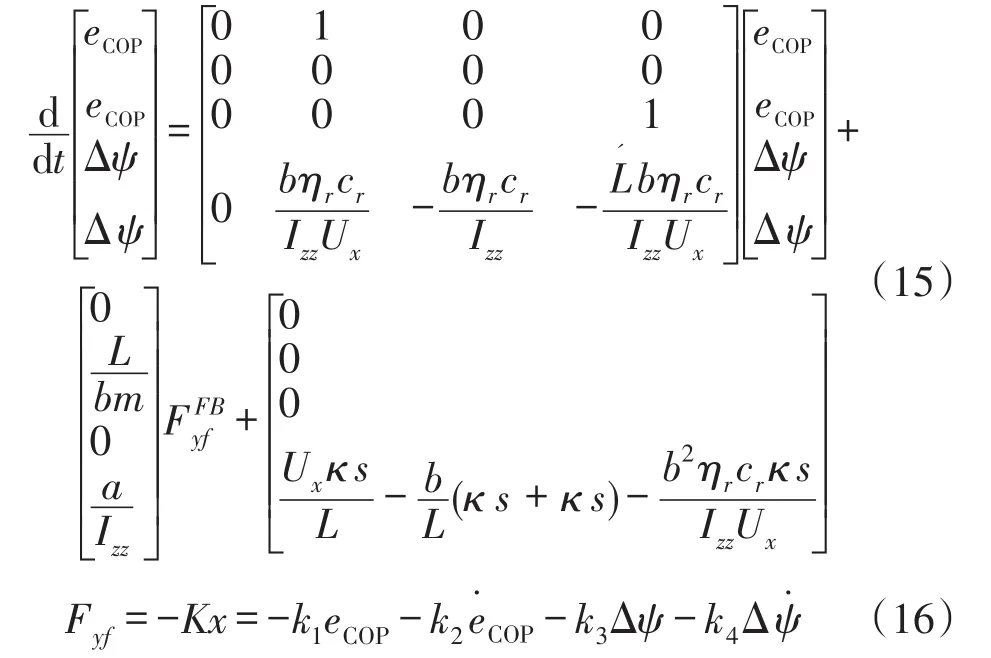
1.3 LQR控制器设计

线性二次型控制理论已成为反馈系统设计的一种重要工具。LQR最优问题为：对于文中的线性系统，确定反馈控制律U*(t)=-KX(t)的最优解，使得如下性能指标最小化：

最优反馈控制律中的状态反馈量为

式中：P可以通过求解代数黎卡提方程（Riccati equation）得到：

由此可见，最优控制器的设计的关键是选取合适的加权矩阵Q和R，并计算出黎卡提矩阵代数方程中的P，求出反馈增益K。

基于所建控制模型，采用最优线性二次型调节器LQR，求得反馈增益并确定出最优反馈控制率。前轮侧偏力Fyf由前轮前馈侧偏作用力与前轮反馈侧偏作用力所确定。前轮侧偏力Fyf通过式（20）被转变为前轮转角输入δ：

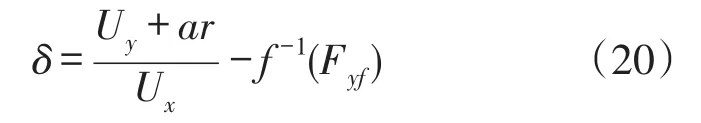
式中：f-1(Fyf)为轮胎力与轮胎滑移相关的逆轮胎模型（轮胎侧偏角与轮胎侧偏力的关系），见图2；r为横摆角速度；Uy为横向速度与Ux为纵向速度。

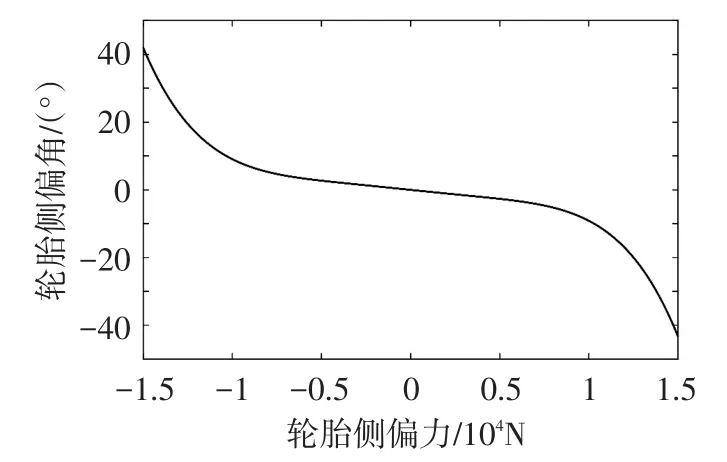
图2 逆轮胎模型

2 Carsim/Simulink联合仿真

2.1 仿真模型建立

Carsim提供了与Simulink联合仿真的接口，通过S函数实现两者的连接通信；可以将Carsim里设置的动力学模型导入到Simulink中，便于在Simu⁃link中设计控制器进行优化仿真。Carsim与Simu⁃link联合仿真模型如图3所示。模块的输入输出在Carsim软件联合仿真界面Import Channel和Export Channel中设置；其中Export代表输出被控制量，即从Carsim输出车辆状态到Simulink控制模块中，实现状态反馈，文中Export channels分别是纵向车速（VxBf_Sm）、横向车速（VyBf_Sm）、道路曲率（Rho_Road）、行驶路径（Station）、横向偏差（lat_A1）、道路头指向（Yaw_CamR）、横摆角速度（AV_Y）、汽车横摆角（Yaw）；Import代表车辆模型的输入，表示车辆状态经过控制器控制后得到一个适合的控制量输入到车辆模型中，实现一个闭环控制，文中Import channels是汽车前左右轮转角（IMP_STEER_L1、IMP_STEER_R1）。

图3 整体仿真模型

整体仿真模型主要由3个模块组成：前馈控制器模块、LQR控制器模块和转角输入模块。前馈控制器模块以道路环境及车身实时运动状态为输入，以前轮前馈侧偏力为输出，如图4a所示；LQR控制器模块以车辆实时状态

为输入，以最优线性二次型调节器LQR确定出的最优反馈控制率为输出，如图4b所示；转角输入模块（corner input）基于转角模型得到，如图4c所示；逆轮胎模型是修正过的轮胎模型，轮胎模型的精确性是实现精确轨迹跟踪控制的关键。

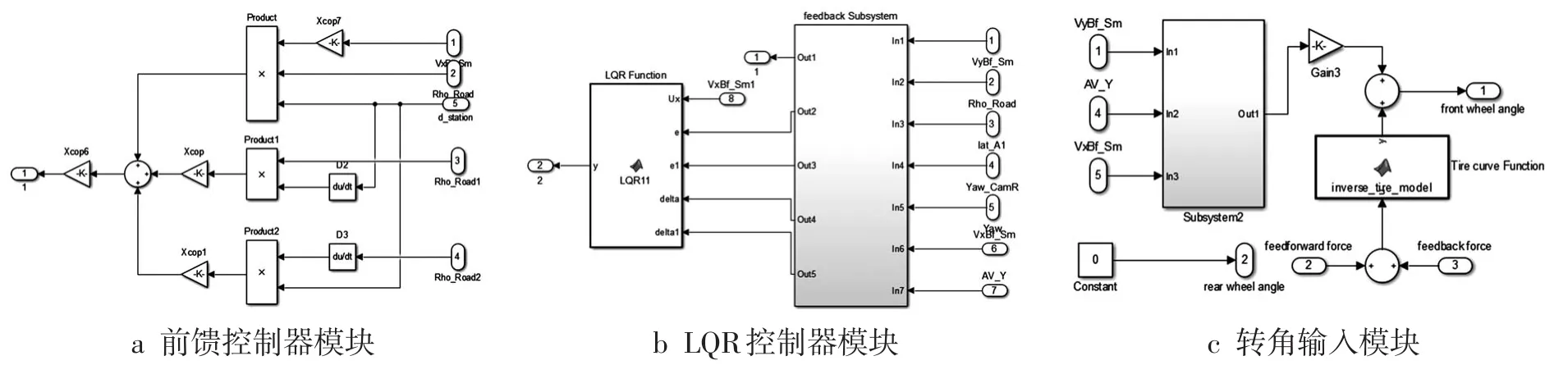
图4 仿真模型的3个模块

2.2 计算头指向误差

自动驾驶车辆轨迹跟踪控制的目标是减少跟踪误差，包括横向偏移和头指向误差。车辆运动时，横向偏移与头指向误差实时反馈到LQR控制器中，确定出的最优反馈控制率来消除误差。横向偏移由Carsim接口横向偏差确定，头指向误差由道路头指向与汽车横摆角确定。如图5所示，θp为道路头指向，θ为汽车头指向（汽车横摆角），头指向误差表示同式（3）。头指向误差根据头指向定义的范围计算，Carsim中头指向被定义为0°～±180°，正方向是从北向东旋转，负方向是从北向西旋转。将实时得到的汽车头指向和道路头指向转换到以正北与正东方向建立的坐标系中，得到道路头指向与汽车头指向所在的坐标象限，再基于头指向实际大小综合得到头指向误差。

图5 头指向误差

2.3 仿真工况设计

1）双移线工况

双移线工况［10］是使用频率较高的一种测试路段，国内外有较多学者以双移线轨迹进行无人驾驶车辆轨迹跟踪能力测试。文中基于双移线工况，对所设计的LQR轨迹跟踪控制器进行仿真测试。

双移线期望横摆角如图6a所示，由参考横向位置Y和参考横摆角φ构成：

图6 双移线工况和8字形工况下的期望横摆角曲线

2）8字形工况

8字形工况由2个圆形路径相切于一点组成，是Carsim自带仿真工况，该工况在日常生活中不常见，但是能对轨迹跟踪控制器的重要特性提供有价值的参考。8字形工况在2个圆相切处有非连续性曲率，当汽车运动到该处时根据运动效果来表明轨迹跟踪控制器的跟踪性能。8字形工况期望横摆角如图6b所示。

3 仿真分析

首先对基于固定增益的前馈-反馈跟踪控制器进行仿真分析。基于固定增益的前馈-反馈跟踪控制器与LQR跟踪控制器的区别在于前轮反馈侧偏力中的反馈增益是基于实验给定的固定值，它不随汽车运行状态的改变而改变。

通过仿真对比LQR控制器，以实际轨迹与期望横摆角跟踪精度来评价上述跟踪控制器的性能。文中以60 km·h-1、70 km·h-1、80 km·h-1的双移线工况与8字形工况进行仿真，路面附着系数为0.8。

当反馈控制模型A矩阵中的参量（纵向速度）变化时，在线LQR根据参数估计结果在线调整反馈控制增益，使系统一直运行在最优控制模式下，在双移线工况下的实时反馈控制增益如图7所示。

图7 反馈控制增益

图8是双移线工况和8字形工况下的轨迹跟踪，图中包含理想跟踪路径与各车速下的实际运动路径。从图8 a～b可以看出：在双移线工况下，固定增益前馈-反馈控制器在高速大曲率转弯时横向偏差会增大，并且在80 km·h-1时有震荡现象，而LQR控制器虽然随车速提高跟踪精度有所下降，但仍能保持高的跟踪精度。由图8 c～d同样可以看出，8字形工况下LQR控制器在各车速下的跟踪精度更高。2种工况下的轨迹跟踪最大横向偏移（理想路径与实际运动路径在同一位置点的横向偏差）如表1所示。在相同工况、相同车速下，LQR控制器有更小的最大横向偏移。车速达到80 km∙h-1时，固定增益前馈-反馈控制器在8字形工况下最大横向偏移达到3.21 m，已偏离理想轨迹。

图8 双移线工况和8字形工况下的轨迹跟踪

表1 轨迹跟随最大横向偏移 m

期望横摆角跟踪即是汽车运动时头指向尽可能跟踪道路头指向（期望道路横摆角），并使跟踪误差最小化。智能车轨迹跟踪能力的评价不仅仅是横向偏移，还要包括期望横摆角跟踪。从图9a和图9c可以看出：在上述2种工况下，LQR控制器的期望横摆角跟踪偏差较小，如表2所示，在80 km·h-1工况下最大横摆角偏差小于4°。与LQR控制器相比，固定增益的前馈-反馈控制器的跟踪偏差较大，并且在拐角过大处出现震荡现象，如图9b所示。固定增益的前馈-反馈控制器在车速60km·h-1和70km·h-1时期望横摆角跟踪误差在4°以下，在80km·h-1工况下跟踪效果急剧变差，难以跟踪期望轨迹。由上述对比可以看出：LQR控制器的横摆角跟踪误差更小，也没有出现震荡现象，说明在高速过弯时有更好的跟踪能力。

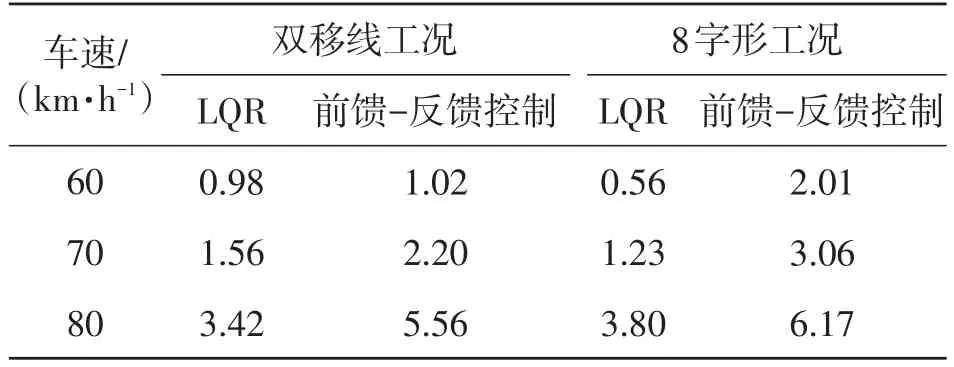
表2 轨迹跟随最大横摆角误差 （°）

图9 双移线工况和8字形工况下的期望横摆角跟踪

4 结论

设计了自动驾驶车辆LQR轨迹跟踪控制器。以二轮自行车模型为基础，以COP为参考点建立控制模型，并将其转变为状态空间形式，对其求解LQR问题获得状态反馈控制率，实现基于LQR控制器的轨迹跟踪控制。在Carsim中设计双移线仿真工况、设置8字形仿真工况，基于LQR控制器需要的控制信号设置信号接口。在Matlab/Simulink中搭建前馈-反馈控制模型，并编写LQR控制算法进行联合仿真。仿真结果显示：设计的LQR轨迹跟踪控制器与固定增益的前馈-反馈控制器相比，在轨迹跟踪控制精度上都有显著的提高，能够满足高速非连续性道路曲率工况下的轨迹跟踪。

［1］余如.无人驾驶车辆的自动转向控制［D］.长春：吉林大学，2016.

［2］陈慧岩，张玉.军用地面无人机动平台技术发展综述［J］.兵工学报，2014，35（10）：1696-1706.

［3］姜岩，龚建伟，熊光明，等.基于运动微分约束的无人车辆纵横向协同规划算法的研究［J］.自动化学报，2013，39（12）：2012-2020.

［4］Nitin R Kapania，J Christian Gerdes．Design of A Feed⁃back-feedforward Steering Controller for Accurate Path Tracking and Stability at The Limits of Handling［J］.Ve⁃hicle System Dynamics，2015，53（12）：1687-1704．

［5］Ziegler J，Bender P，Schreiber M，et al.Making Bertha Drive An Autonomous Journey on A Historic Route［J］.IEEE Intelligent Transportation Systems Magazine，2014，6(2)：8-20．

［6］尹晓丽，李雷，贾新春.无人驾驶汽车路径跟踪模糊预测控制［J］.中北大学学报（自然科学版），2011，32（2）：135-138.

［7］Levinson J，Askeland J，Becker J，et al.Towards Fully Au⁃tonomous Driving:Systems and Algorithms［C］∥ 2011 IEEE Intelligent Vehicles Symposium（IV）.Spain:IEEE，2011：163-168.

［8］赵寿华，永磁同步电机高性能控制系统研究［D］.杭州：浙江大学，2015.

［9］Kritayakirana K，Gerdes J C.Using The Centre of Percus⁃sion To Design A Steering Controller for An Autonomous Race Car［J］.Vehicle System Dynamics，2012，50（S1）：33-51．

［10］龚建伟，徐威.无人驾驶车辆模型预测控制［M］.北京：北京理工大学出版社，2014：129-130.

Design of LQR Trajectory Tracking Controller for Autonomous Vehicle

Tao Bingbing,Zhou Haiying,Wang Sishan
（Hubei University of Automotive Technology,Shiyan 442002,China）

To improve the control precision of the intelligent vehicle,the feedforward-feedback control model was established with the Center of Percussion（COP）as the reference point.The LQR（Linear Quadratic Regulator）problem was solved with the control model,and the rate of the state feedback con⁃trol was obtained to achieve the optimal control.Under the double-shift condition and 8-gauge condi⁃tion,the LQR trajectory tracking controller was simulated with Matlab/Simulink and Carsim.The result shows that the LQR trajectory tracking controller has higher control precision,comparing with the fixed gain feedforward-feedback controller.

automatic driving;trajectory tracking;LQR controller;Carsim/Matlab simulation

TP273；U463.6

A

1008-5483（2017）04-0001-06

10.3969/j.issn.1008-5483.2017.04.001

2017-06-06

湖北省自然科学基金项目（2015CFB686）；湖北省技术创新专项重大项目（2017AAA027）；

湖北省教育厅科学研究指导性项目（B2015121）

陶冰冰（1990-），男，湖北孝感人，硕士生，从事无人驾驶智能车纵横向控制方面的研究。E-mail:1477416188@qq.com