舰载雷达天线电子稳定方程在三轴稳定转台雷达上的应用分析

吕向阳

(中国船舶重工集团公司第七二四研究所，南京 211153)

舰载雷达天线电子稳定方程在三轴稳定转台雷达上的应用分析

吕向阳

(中国船舶重工集团公司第七二四研究所，南京 211153)

通过对平台罗经和雷达稳定转台的结构分析，说明大地极坐标系与雷达稳定转台极坐标系之间的二阶电子稳定方程与实际设备空间运动情况比较符合。通过剩余误差法和二阶电子稳定方程的对比分析，在三轴稳定转台雷达的补偿修正中，当纵、横摇剩余误差的瞬时值<1°时，采用舰载雷达天线电子稳定方程的剩余误差法可以直接作为二阶电子稳定方程的替代方案应用。

舰载雷达;电子稳定方程；平台罗经；三轴稳定转台

0 引 言

采用三轴稳定转台(纵摇轴、横摇轴和方位轴)的舰载雷达一般安装在舰船主桅杆区。受到质量、体积的限制，同时受到风载荷的影响，易导致一次稳定后的平台剩余误差大，不利于雷达整体精度的提高。为了提高精度，可以将平台剩余误差引入舰载雷达天线电子稳定方程进行二次修正，也可以应用大地极坐标系与稳定转台极坐标系之间的二阶电子稳定方程进行直接修正。

1 姿态角的定义与设备的机械结构

1.1 姿态角的定义

(1) 纵摇角 舰艏艉线与其在水平面内的投影线在铅垂面内的夹角，舰艏抬高为正，记为P；

(2) 横摇角 舰甲板平面绕舰艏艉线轴线旋转的角度，舰右舷向下为正，记为R；

(3) 航向角 舰艏艉线在水平面内的投影与正北之间的夹角，自正北算起，顺时针方向为正，记为H。

(4) 雷达稳定转台纵摇角 框架横摇轴线与其在舰船甲板平面内的投影线在垂直舰船甲板面内的夹角，指向舰艏，轴线下降为正，记为P′；

(5) 雷达稳定转台横摇角 横摇框架平面绕框架横摇轴线旋转的角度，舰右舷向上为正，记为R′；

(6) 雷达稳定转台航向角 框架横摇轴线在舰船甲板平面内的投影与舰艏艉线之间的夹角，自舰艏算起，顺时针方向为正，记为H′。

1.2 平台罗经的机械结构[1]

平台罗经由机械平台和陀螺仪组成。机械平台包含基座、横摇稳定框架、纵摇稳定框架和台体。机械平台的基座就是船体。横摇稳定框架的轴线与舰船艏艉线平行，安装在基座上的一对轴承上，受横摇稳定回路控制，产生绕框架横摇轴线的运动保持纵摇稳定框架和台体的稳定。纵摇稳定框架的轴线与横摇稳定框架的轴线在横摇框架平面内保持垂直，安装在横摇稳定框架上的一对轴承上，受纵摇稳定回路控制，产生绕框架纵摇轴线的运动保持台体的稳定。通过横摇稳定框架和纵摇稳定框架，机械平台的台体可以始终处于水平位置。

1.3 雷达稳定转台的机械结构

雷达稳定转台的机械结构包含基座、横摇稳定框架、纵摇稳定框架和方位转台。稳定转台的基座就是船体。横摇稳定框架的轴线与舰船艏艉线平行，安装在基座上的一对轴承上，受横摇稳定回路控制，产生绕框架横摇轴线的运动保持纵摇稳定框架和方位转台的稳定。纵摇稳定框架的轴线与横摇稳定框架的轴线在横摇框架平面内保持垂直，安装在横摇稳定框架上的一对轴承上，受纵摇稳定回路控制，产生绕框架纵摇轴线的运动保持方位转台的稳定。方位转台在空间的位置姿态由横摇稳定框架和纵摇稳定框架决定。

1.4 相互间的运动关系

1.4.1 从设备结构分析

从平台罗经的机械结构可以看出，罗经送出的舰船姿态角(纵摇角、横摇角和航向角)满足姿态角的定义，即台体始终处于水平面内，纵摇角始终在大地铅垂面内，航向角始终在大地水平面内，横摇角由于横摇稳定框架的位置决定始终在舰船肋骨面内。由于罗经纵横摇框架控制误差极小，在分析时可以忽略。根据一个姿态角对其他姿态角影响关系的判断依据是指该姿态角是否影响其他姿态角在空间中的运动走向，可以得到横摇角变化不影响纵摇角和航向角。纵摇角的变化不影响航向角，但影响横摇角。航向角的变化影响纵摇角和横摇角[2]。

从雷达稳定转台的机械结构可以看出，雷达稳定转台姿态角(纵摇角、横摇角和航向角)的运动平面不全部与舰船姿态角的运动平面重合。只有雷达稳定转台横摇角受到结构位置的决定，其运动平面与罗经送出的舰船横摇角的运动平面始终重合。雷达稳定转台横摇角的运动平面由于横摇稳定框架的结构位置决定始终在舰船肋骨面内。

雷达稳定转台纵摇角在垂直于舰甲板平面的平面内，不能始终保持在大地铅垂面内。实际使用中雷达稳定转台纵摇角的运动平面在大地铅垂面左右摆动，因此不满足舰船姿态角的定义。在大地铅垂面内的等效纵摇角是雷达稳定转台纵摇角在大地铅垂面内的投影。投影夹角为横摇角与雷达稳定转台横摇角的差，即(R-R′)，如图1所示。

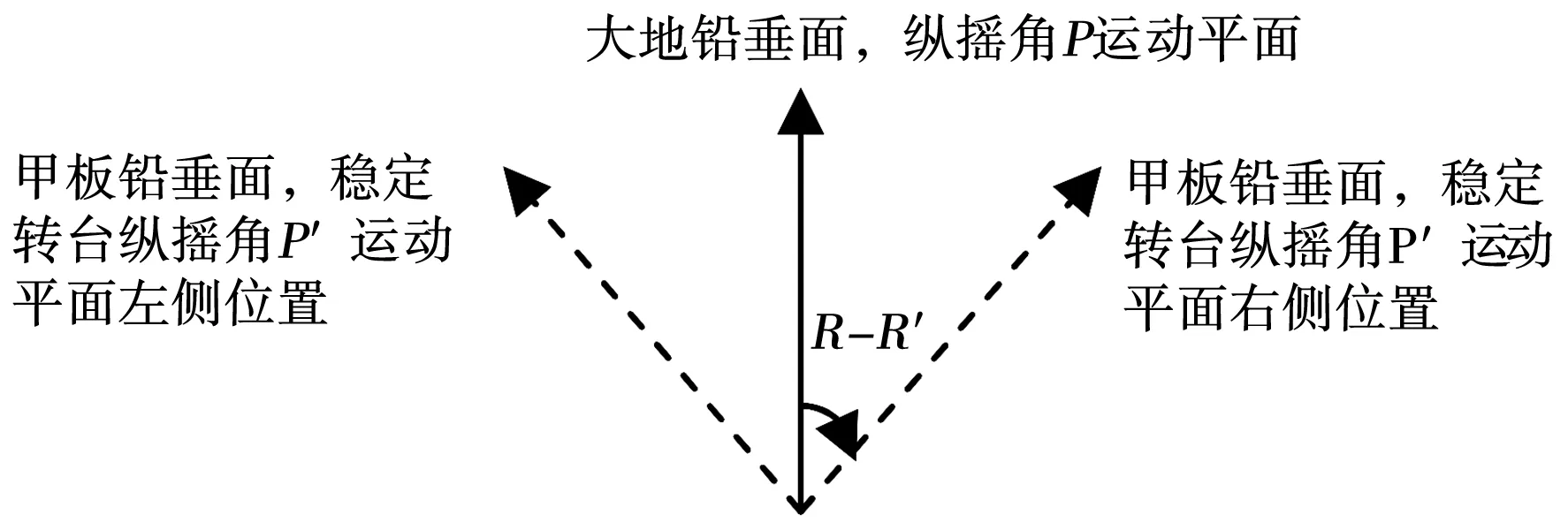
图1

由于雷达稳定转台寄生在舰船甲板平面上，因此雷达稳定转台航向角是在舰船甲板平面内，也不能始终在大地水平面内。根据一个姿态角对其他姿态角影响关系的判断依据可以看出，稳定转台纵摇角变化不影响稳定转台横摇角和稳定转台航向角，稳定转台横摇角变化不影响稳定转台航向角而影响稳定转台纵摇角，稳定转台航向角变化影响稳定转台横摇角和稳定转台纵摇角。

1.4.2 通过二次电子稳定分析

通过观察大地极坐标系与舰船甲板极坐标系之间的二次电子稳定方程也可以发现以上现象。方程揭示了横摇角对纵摇角的影响，即当横摇没有完全克服舰船摇摆时(R≠R′)，即使P′=P，此时也不能表示完全克服舰船纵摇摇摆，消除了舰船纵摇的影响。这也提示舰船纵摇和稳定平台纵摇不是总在一个平面内。在采用三轴稳定转台的雷达上，完全克服舰船纵摇的前提是首先必须完全克服舰船的横摇影响。

2 两种电子稳定方程在雷达上的应用

2.1 剩余误差法

如果在实际使用中不考虑舰船纵摇角与雷达稳定转台纵摇角不总在一个面内的影响，直观认为二者始终在一个平面内，即始终在大地铅垂面内，则可以直接利用大地极坐标系与舰船甲板极坐标系之间的电子稳定方程进行二次修正，提高雷达精度。将纵摇剩余误差(P-P′)、横摇剩余误差(R-R′)作为纵摇、横摇代入方程，得到大地极坐标系向雷达稳定转台极坐标转换：

XP1=cosE[sin(R-R′)sin(P-P′)cos(A-H)+

cos(R-R′)sin(A-H)]-sinEsin(R-R′)cos(P-P′)

(1)

YP1=cosEcos(P-P′)cos(A-H)+sinEsin(P-P′)

(2)

ZP1=cosE[sin(R-R′)sin(A-H)-cos(R-R′)sin(P-P′)·cos(A-H)]+sinEcos(R-R′)cos(P-P′)

(3)

得

Ap1=tan-1(XP1/YP1)

(4)

Ep1=sin-1(ZP1)

(5)

雷达稳定转台极坐标系向大地极坐标系转换：

X1=sinECsin(R-R′)+cosECcos(R-R′)sinAC

(6)

Y1=cosEC[cos(P-P′)cosAC+sin(P-P′)sin(R-R′)·sinAC]-sinECsin(P-P′)cos(R-R′)

(7)

Z1=cosEC[sin(P-P′)cosAC-cos(P-P′)sin(R-R′)·sinAC]+sinECcos(P-P′)cos(R-R′)

(8)

得

A1=tan-1(X1/Y1)+H

(9)

E1=sin-1(Z1)

(10)

2.2 二次电子稳定方程

将舰船甲板看成是大地，将机械稳定转台看成舰船甲板，将电子稳定方程进行两次坐标转换，推导出大地极坐标与雷达天线稳定转台极坐标之间的转换方程。

大地极坐标系向雷达稳定转台极坐标转换：

Xp=cosE[sinPsin(R-R′)cos(A-H)+cos(R-R′)sin(A-H)]-sinEcosPsin(R-R′)

(11)

Yp=cosE[cosP′cosPcos(A-H)+sinP′sinPcos(R-R′)cos(A-H)-sinP′sin(R-R′)sin(A-H)]+

sinE[cosP′sinP-sinP′cosPcos(R-R′)]

(12)

Zp=cosE[sinP′cosPcos(A-H)-cosP′sinPcos(R-R′)cos(A-H)+cosP′sin(R-R′)sin(A-H)]+

sinE[sinP′sinP+cosP′cosPcos(R-R′)]

(13)

得

Ap=tan-1(Xp/Yp)

(14)

Ep=sin-1(Zp)

(15)

雷达稳定转台极坐标系向大地极坐标系转换：

X=cosEcosAC[-sinP′sin(R-R′)]+cosECcos(R-R′)·sinAC+sinEC[cosP′sin(R-R′)]

(16)

Y=cosECcosAC[cosPcosP′+sinPsinP′cos(R-R′)]+cosECsinAC[sinPsin(R-R′)]+

sinEC[cosPsinP′-sinPcosP′cos(R-R′)]

(17)

Z=cosECcosAC[sinPcosP′-cosPsinP′cos(R-R′)]-cosECsinAC[cosPsin(R-R′)]+

sinEC[sinPsinP′+cosPcosP′cos(R-R′)]

(18)

得

A=tan-1(X/Y)+H

(19)

E=sin-1(Z)

(20)

2.3 两种算法对比分析

通过剩余误差法和二阶电子稳定方程对比，将Ap与Ap1、Ep与Ep1、A与A1、E与E1进行比较分析。为了便于推导计算将其转换为tan(Ap)与tan(Ap1)、 sin(Ep)与sin(Ep1)、tan(A)与tan(A1)、 sin(E)与sin(E1)，然后再作三角函数逆变换。推导得出

│sin(ΔEp)│=│sin(Ep1)-sin(Ep)│<

sin(R)(1-cosP′)

(21)

│tan(ΔAp)│=│tan(Ap1)-tan(Ap)│<

sin(P)sin(R-R′)

(22)

│sin(ΔE)│=│sin(E)-sin(E1)│<

sin(R)(1-cosP′)

(23)

│tan(ΔA)│=│tan(A1)-tan(A)│<

sin(P)sin(R-R′)

(24)

从式(21)、(22)、(23)和(24)推导结果得出

│sin(ΔE)│=│sin(ΔEp)│

=│sin(Ep1)-sin(Ep)│<

sin(R)(1-cosP′)

(25)

│tan(ΔA)│=│tan(ΔAp)│

=│tan(Ap1)-tan(Ap)│<

sin(P)sin(R-R′)

(26)

通过式(25)、(26)估算出Ap与Ap1、Ep与Ep1、A与A1、E与E1之间的差异大小：

(1) 当雷达稳定转台克服舰船摇摆后，即机械平台稳定一次后，此时纵、横摇剩余误差瞬时值最大可达±1°。取横摇剩余误差R-R′的瞬时最大值1°、纵摇角P最大值5°、横摇值R最大值20°、稳定转台纵摇角P′最大值5°进行估算：

│sin(ΔE)│=│sin(ΔEp)│

=sin(20°)(1-cos5°)=0.00137

│tan(ΔA)│=│tan(ΔAp)│

=sin(5°)sin(1°)=0.00153

得

ΔE

ΔA

计算结果可看出，对于采用三轴稳定转台的舰载雷达，机械平台进行一次稳定后，即纵摇剩余误差的瞬时值<1°、横摇剩余误差的瞬时值<1°)时，可以采用剩余误差法，直接将平台剩余误差(纵摇误差、横摇误差)作为纵摇值和横摇值引入舰载雷达天线电子稳定方程进行二次修正，也可以直接应用大地极坐标系与稳定转台极坐标系之间的二阶电子稳定方程进行修正。在这种情况下，由于采用的修正方程不一致所引入的俯仰角误差ΔE和方位角误差ΔA相差不大，处于可以接受的范围。也就是说，当纵、横摇剩余误差的瞬时值<1°时，在采用三轴稳定转台雷达的补偿修正中，采用舰载雷达天线电子稳定方程的剩余误差法可以直接作为二阶电子稳定方程的替代方案应用。

(2) 当雷达稳定转台在某一方位区域下倾时，方位转台相对于大地的纵摇剩余误差瞬时值可达±5°，横摇剩余误差瞬时值可达±20°。取横摇剩余误差R-R′的瞬时最大值20°、纵摇角P最大值5°、横摇值R最大值20°、稳定转台纵摇角P′最大值5°进行估算。

│sin(ΔE)│=│sin(ΔEp)│

=sin(20°)(1-cos5°)=0.00137

│tan(ΔA)│=│tan(ΔAp)│

=sin(5°)sin(20°)=0.0298

得

ΔE

ΔA

计算结果可看出，由于采用的修正方程不一致，引入的俯仰角误差ΔE还是在可以接受的范围内，但方位角误差ΔA会明显变大，最大可达到1.71°，不可忽略其影响。因此，为了不引入由于采用的修正方法不同而带来的系统误差，此时最好直接应用大地极坐标系与雷达稳定转台之间转换的二阶电子稳定方程来进行雷达的修正。

3 结束语

本文对剩余误差法和二阶电子稳定方程在舰载雷达稳定转台上的应用进行了对比分析，并初步对两种算法所引入的误差进行了估算，希望能给电子稳定方程的应用提供一些有益的参考。

[1] 谢韶旺,陈其廉,李庆芬.平台罗经框架结构的动力响应分析[J].哈尔滨工程大学学报, 2006,27(5).

[2] 冯同玲,陈龙潭. 舰载雷达天线电子稳定方程的推导与分析[J].火控雷达技术,2001(30).

[3] 方成一，王振旺. 舰载雷达天线电子稳定方程的推导方法[J].雷达与对抗,1999(2).

[4] 曹正才. 舰载雷达常用稳定方式坐标变换[J].雷达与对抗,2010(1).

[5] 张润逵.雷达结构与工艺(上册)[M].北京：电子工业出版社，2007.4

[6] 张志远，罗国富. 舰船姿态坐标变换及稳定补偿分析[J].舰船科学技术,2009,31(4).

Application of electronic stabilization equation of shipborne radar antenna in radars with three-axis stabilizing rotary platform

LYU Xiang-yang

(No.724 Research Institute of CSIC, Nanjing 211153)

By analyzing the structure of the platform gyrocompass and the radar stabilizing rotary platform, it is shown that the two-order electronic stabilization equation between geodetic polar coordinate system and radar polar coordinate system of the stabilizing rotary platform is in good agreement with the actual space motion of the equipment. With the comparison and analysis of the residual error method and the two-order electronic stabilization equation, in the compensation and correction of the radars with the three-axis stabilizing rotary platform, when the instantaneous pitch and roll residual error values are less than 1°, the residual error method of using the electronic stabilization equation for the shipborne radar antenna can be directly used as an alternative solution of the two-order electronic stabilization equation .

shipborne radar; electronic stabilization equation; platform gyrocompass; three-axis stabilizing rotary platform

TN820.3

A

1009-0401(2017)04-0054-04

2017-08-10；

2017-08-22

吕向阳(1975-)，男，高级工程师，研究方向：雷达伺服。