光学侦察卫星任务时效性评估研究

赵程亮，张占月，赵 双，刘 瑶

(1.装备学院 研究生管理大队，北京 101416；2.装备学院 航天指挥系，北京 101416)

光学侦察卫星任务时效性评估研究

赵程亮1，张占月2，赵 双1，刘 瑶1

(1.装备学院 研究生管理大队，北京 101416；2.装备学院 航天指挥系，北京 101416)

卫星任务时效性直接影响卫星的任务效益,针对光学侦察卫星任务流程，详细分析任务相关环节并建立了数学模型;从时间链上对侦察卫星姿态调节时间、过境时间、数据下传时间三个任务环节进行了仿真计算，并比较了多颗卫星对具体观测任务的相关时效差异以及相关影响因素，有效反映了侦察卫星任务效能，为光学侦察卫星任务时效性分析及效能评估提供了依据，对卫星观测任务方案时间任务效能分析预评估有重要的应用价值。

光学侦察卫星；任务流程；时效性；效能评估

0 引言

在现代战争中，侦察卫星发挥的作用越来越重要，其作战应用的深度不断加深，广度不断拓展，是获取信息情报来源的重要侦察工具[1]。战场上的争分夺秒对侦察卫星的观测时间有着极为严格的时间要求，信息情报获取的时间每一秒都极为宝贵。因此，分析光学侦察卫星从接收任务指令到完成观测数据下传这样一个任务流程时间有重要的应用指导意义，更方便的供指挥员斟酌参考、决策指挥[2]。

光学侦察卫星是通过卫星星载照相机或摄像机等侦察观测设备，从轨道对目标实施侦察、监视以及搜集地面信息。本文以光学侦察卫星为研究对象，从卫星接收任务指令开始到卫星数据下传完毕对卫星任务观测过程时效性进行详细分析与评估。因卫星在接收指令后，卫星任务期间的在轨飞行时间与具体任务、卫星轨道参数有关，在此不再建模求解。主要考虑建立卫星姿态调整、卫星过境成像、卫星数据下传等卫星任务流程相关数学模型，最后结合具体任务实例对卫星的观测任务时效进行仿真验证。

1 卫星载荷侧摆调节时间计算模型

1.1 侦察目标在地固系下的坐标

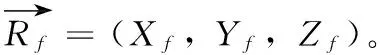
(1)

由于地球的形状并不是规则圆球体，所以上式中Re取地球平均半径会引起较大误差，考虑地球形状下的地球半径[4]为：

(2)

Rα、Rα为地球的赤道半径与极半径。

1.2 侦察卫星在地固系下的坐标

上一下小节计算给出了侦察目标在地心固连坐标系下的坐标计算数学模型，在本小节将建立侦察卫星在地心固连坐标系下的坐标，由此计算卫星侧摆角度。其主要思路是首先求得卫星在地心惯性坐标系下的坐标，然后由地心惯性坐标系与地心固连坐标系的转换关系求得卫星在地心固连坐标系下的坐标。卫星在任意时刻的地心距r为：

(3)

式中，a为轨道半长轴，e为偏心率，f为真近地点角。

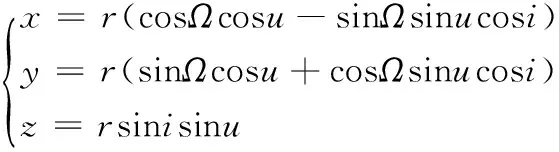
(4)

式中,Ω为升交点赤经，u为纬度幅角，r为地心距，i为轨道倾角

设Φ0为初始时刻t0地球惯性坐标系与地球固连坐标系的夹角，ω为地球自转角速度，则t时刻地惯系与地固系的夹角为：

Φ(t)=Φ0+ω(t-t0)

(5)

由地心固连坐标系与地心惯性坐标系的转换关系[5]可知卫星在地心固连坐标系下的坐标

(6)

由此便知道了地面观测目标与卫星任意时刻在地固系下的坐标，并求得卫星的侧摆角度θ。设卫星侧摆角速度为ω，则卫星侧摆时间为：

(7)

2 卫星单次过境观测时间计算模型

卫星单次过境观测时间[6]指的是卫星接收任务指令开机并调整好姿态后对观测目标地点进行观测的时间窗口。观测时间与卫星的轨道参数和目标区域的大小有关。当前大多数光学侦察卫星观测都是以扫描方式进行成像[7]，由于卫星的在轨高速运动，卫星过境时间非常短暂。卫星单次过境如图1所示，卫星由A点飞往D点，当卫星与目标区域仰角为φ时开始观测，卫星观测时间窗口为AD段，B、C为卫星在目标区域正上方的位置。目标区域EF的纬度跨度为Φ。

图1 卫星单次过境观测

由于卫星的观测时间非常短暂，在此认为卫星在成像时间窗口内速度与轨道高度为定值，卫星在成像窗口内轨道高度为：

(8)

当前时刻卫星速度大小为：

(9)

式中,μ为地球引力常数，f为真近地点角。R为地球半径，a为轨道半长轴，e为轨道偏心率。

由于目标区域两侧仰角φ相同，所以AD段长度计算公式为：

AD=AB+BC+CD=2AB+EF

(10)

将△ABE近似看做直角三角形，则：

(11)

EF=ΦR

(12)

则卫星单次过境观测时间为：

(13)

3 卫星数据下传时间计算模型

卫星在完成观测任务并调整好姿态以后，需要到达地面站接收范围将观测数据进行数据下传[8]。如图2所示，卫星在到达T1时刻时，地面站开始准备进行数据接收。在T2时刻地面站可以捕捉到卫星信号，但此时信号强度不足以完成传输。在T3时刻，地面站可以稳定捕获到卫星并完成稳定跟踪与数据传输，传输时间为T3到T4时刻的这段时间。T5时刻脱离地面站控制范围并完成任务。

由此计算卫星数据下传时间以确定卫星是否能够在数传时间T3-T4这段时间内完成数据传输具有重要参考意义。卫星数传时间与数据信息量大小和数传速率有关，数据信息量主要与卫星观测成像面积以及成像分辨率有关。

3.1 卫星观测覆盖区域面积计算

侦察卫星在经过目标区域进行过境观测时开始进行观测成像，在顺着星下线以某一侧摆角度形成一条观测条带，观测条带的信息即为初始成像数据信息。卫星观测条带面积与卫星遥感器性能、轨道特性、侧摆情况有直接关系，成像面积是计算卫星成像信息量的基础。如图3所示，卫星在t1时刻星下点为N点，侧摆角度为θ，在观测时间内卫星扫描过的面积为矩形ABA1B1。因此，若想求得卫星观测的覆盖面积，便首先需要求出观测条带扫描距离[9]。

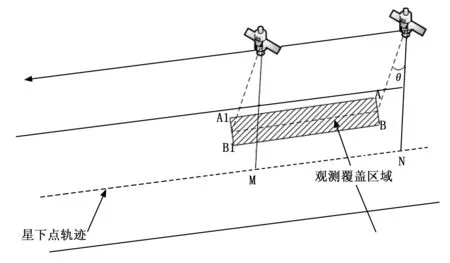
图3 卫星单次过境覆盖区域

由于卫星的观测条带平行于卫星的星下点轨迹，所以AA1=BB1=MN，故只需要计算出卫星过境观测条带的长度。卫星观测条带的长度与卫星在开始观测与结束观测的两个时间节点的星下点有关。侦察卫星在地心轨道坐标系中的坐标为(r，0，0)，由地心轨道坐标系到地心惯性坐标系之间的转换可知卫星在地心惯性坐标系下的坐标为：

式中,Ω为升交点赤经，i为轨道倾角，u为纬度幅角，由地心惯性坐标系到地心固连坐标系下转换为：

(14)

θ为当前时刻地心固连坐标系与地心惯性坐标系下的夹角。

由卫星星下点在地心固连坐标系中的坐标可以求得星下点的经纬度[10]：

(15)

如图4所示，已知AB两点的经纬度坐标A(λ1,φ1)B(λ2,φ2)，N为北极点，O为地球半径。在球面三角形NAB中：

(16)

AB对应的弧长为：

r=arcAB·RE

(17)

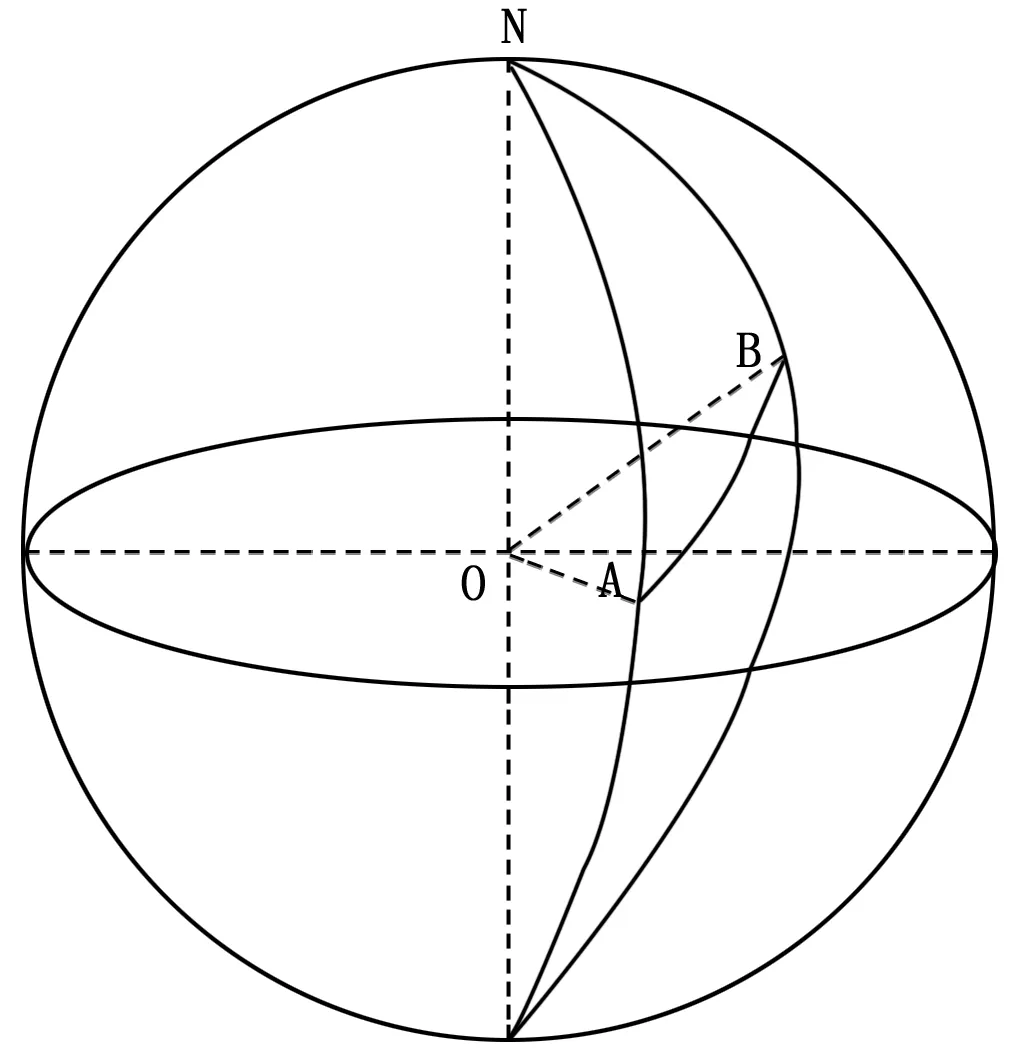
图4 地球任意两点球面距离

计算卫星观测条带宽度如图5所示，s为卫星在t时刻位置，A为卫星星下点轨迹，θ为卫星载荷侧摆角度，Δg为卫星视场角，LR长度即为卫星观测条带的宽度。

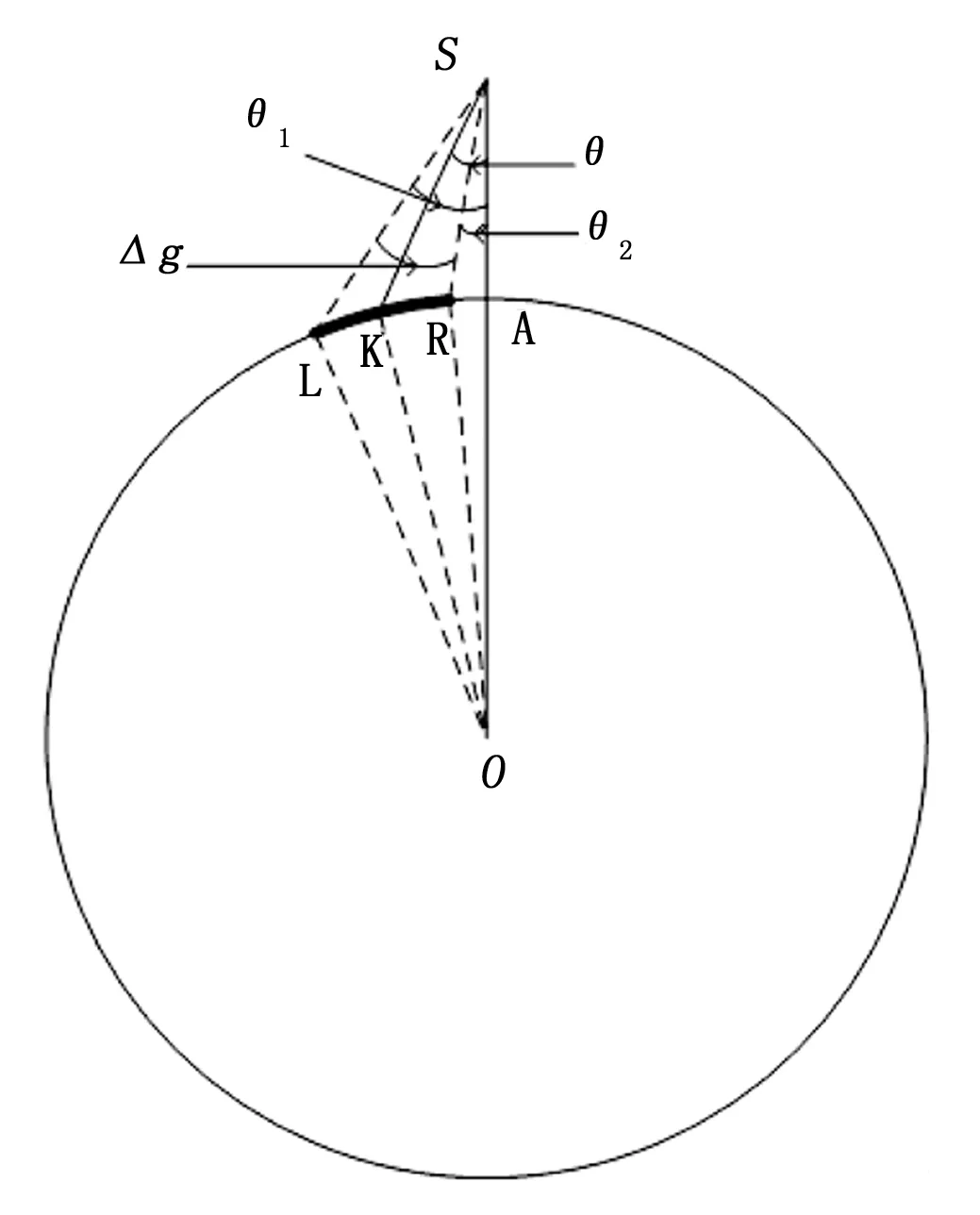
图5 侦察卫星成像侧视图

在△SRO中：

(18)

(19)

(20)

H为卫星当前轨道高度，RE为地球半径同理可求得SL。

将LR视为直线，在△SLR中：

(21)

3.2 地面站对侦察卫星可见性判断计算模型

侦察卫星沿着预定轨道高速运行，受限于地球的遮挡和地面站设备性能参数，对于地面某一地面站来说，侦察卫星在某个圈次，对于地面站的可见性只有两种情况，不可见或者一段可见，并且可见弧段的长短与卫星的轨道参数、地面站位置、及测控设备相关。地面站与航天器之间的可见性取决于地面站与航天器之间的仰角。当卫星与地面站大于最小仰角临界值αmin与最大仰角临界值αmax的时候，地面站与卫星可见，此时可以进行数据传输。

设地面站经纬度坐标为(λ,φ)，则由式(1)可得地面站在地心固连坐标系下的坐标(xt,yt,zt)。根据卫星的轨道根数以及式(6)，便可得出卫星在地心固连坐标系下的直角坐标(xs,ys,zs)，此时由航天器与地面站之间的距离d、地球半径Re、以及地心距r可计算得出地面站与航天器连线和地面站与地心连线之间的张角α1，仰角与张角之间相差90°即：

(22)

显然，如果αmin≤α1-90°≤αmax，则此时卫星与地面站之间可进行数据传输，否则两者之间不可见，不能进行数据传输以及相应的跟踪控制。

3.3 光学侦察卫星信息下传时间计算

光学侦察卫星在获取地面影像信息后，一般先将成像信息进行存储，在与地面站或中继卫星满足可传输条件的情况下，进行数据下传。因此卫星信息数据下传时间为：

Trd=Tw+Td

(23)

式中,Tw为卫星侦测信息后数据等待下传时间，Td为与地面站满足可传输条件后信息下传时间。

卫星侦测信息后数据等待下传时间Tw主要根据卫星与地面站可见性来确定，在此采用仿真计算方法，具体实现步骤如下：

1)根据地面站可用数量确定推进步长和仿真周期，其中步长根据具体任务精确度来确定，仿真周期为对信息延迟的最大忍受时间。

2)推进步长，由3.2节所述方法判断卫星与地面站的可见性，若可见则跳出循环，反之继续。

3)判断是否达到仿真周期，未达到则继续推进步长，反之返回，Tw超过最大限定时间，判定无效。

信息下传时间Td主要与成像信息数据量大小以及数据下

表1 卫星相关性能指标

表2 仿真计算结果

传速率来决定。数据信息量大小与卫星成像面积，卫星影像分辨率有关。光学成像侦察卫星获取的信息量I(单位为bit)[8]计算公式为：

(24)

kp为图像压缩比；kb为波段数；Ag为成像面积；rg为地面分辨力；Cn为每象元灰度数；Bn为每象元亮度数。

卫星信息传输速率为v,则卫星影像信息传输时间为：

Td=I/v

(25)

4 仿真计算实例

卫星观测目标区域纬度范围为[37°N,38°N]，经度范围为[119°E,120°E]。地面站坐标(122°，49°)仿真时间为2017年3月20日04:00至2017年3月21日04:00，卫星参数参照美国”数字全球”公司商业遥感系列卫星[11]，相关卫星性能参数如表1所示：

利用表1卫星性能指标，结合所建立卫星姿态调节时间计算模型、卫星过境时间模型、数据下传时间模型，同时基于卫星的星历参数及地球椭球模型，仿真计算结果如表2所示。

仿真计算结果从卫星侧摆角度、侧摆时间、卫星过境时间、成像面积、信息等待下传时间、数传时间、执行任务时间七个方面进行比较分析。由计算结果可知，卫星针对同一目标区域的侧摆角度相差不大，由此所需要的侧摆调节时间小有差异。在卫星过境成像时间上，过境时间长短主要与目标区域大小以及卫星轨道高度有关，由于四颗卫星轨道高度之间相差不大以及在轨高速飞行，使得仿真结果中过境时间非常接近。卫星成像条带面积与卫星的成像扫描宽度以及成像时间有关，在不考虑实时数据下传的情况下(侦察同时进行数据下传)，同时又会受限于最大成像条带距离以及卫星星上存储容量。WorldView-2在针对同一任务中具有最大观测条带，其主要原因为拥有最大的成像扫描幅宽(17.6km)，其他卫星成像扫描幅宽分别为16.4km、16.5km、15.2km。QuickBird-2卫星在成像面积上与其他观测卫星具有较大偏差，这是由于QuickBird-2号卫星单次观测条带最高为165km。信息等待下传时间方面，该时间主要受限于卫星轨道要素以及地面站的地理位置分布，会因具体任务具体可用卫星资源以及地面站约束条件变化，因此要具体任务具体分析，找出最适合本次观测任务的方案。GeoEye-1卫星在数传时间上明显高于其他卫星，其原因是因为GeoEye-1卫星具有较高地面分辨率，影像质量较高，信息量大。故GeoEye-1卫星在任务时效性上有较大差异。总任务时间是最能反应卫星任务执行时效性的重要因素，在观测任务满足分辨率约束条件以及覆盖性等约束条件基础上上，卫星任务时效性是最能反映任务效率的评估指标。在本次仿真结果中可以看出GeoEye-1卫星在执行本次观测任务中具有最优任务时效性能。

5 结论

本文针对成像侦察卫星任务应用流程，从卫星接收指令上传开始至卫星数据下传结束。对卫星任务流程各个环节进行详细分解并建立相关数学模型，对卫星的各个任务环节时效性进行了仿真分析。并比较了多星对具体观测任务的完成能力，详细分析了影响任务时效性的各个约束条件。为成像侦察卫星时效性评估提供依据。但在模型细节上仍然有待完善，比如在卫星姿态调节模型上没有建立卫星姿态稳定相关模型，有待于更深一步研究。

[1] 李 智，张占月，孙 琰.现代太空战[M]. 北京：国防大学出版社，2016.

[2] Nielsen P E. 太空武器[M]. 张占月，张志威，唐立文,译. 北京：国防工业出版社，2014.

[3] 郭 浩，邱涤珊，黄 维. 调姿时间对敏捷成像卫星任务规划影响仿真[J]. 装备指挥技术学院学报，2012，23(1)：70-74.

[4] 仲惟超. 航天器轨道和姿态参数对光学成像的影响分析[D].哈尔滨:哈尔滨工业大学，2009.

[5] 盛卫东. 天基光学监视目标跟踪技术研究[D]. 长沙:国防科学技术大学，2011.

[6] 郝会成. 敏捷卫星任务规划问题建模及求解方法研究[D]. 哈尔滨:哈尔滨工业大学，2013.

[7] 徐一帆. 天基海洋移动目标监视的联合调度问题研究[D].长沙:国防科学技术大学,2011.

[8] 赵和鹏. 多地面站卫星数据接收任务规划问题研究[D]. 电子科技大学，2013.

[9] 贺仁杰，李菊芳，姚 锋. 成像侦察卫星任务规划技术[M]. 北京：科学出版社，2010.

[10] 曹裕华，冯书兴，管清波. 航天器军事应用建模与仿真[M]. 北京：国防工业出版社，2010.

[12] 李 颖，杨 庆，卢 雪.国外典型航天系统手册[M]. 北京：国防工业出版社，2016.

Evaluation for Mission Timeliness of Optical Reconnaissance Satellite

Zhao Chengliang1，Zhang Zhanyue2，Zhao Shuang1，Liu Yao1

(1.Department of Graduate Management，Equipment Academy，Beijing 101416，China;2.Department of Space Command，Equipment Academy，Beijing 101416，China)

The timeliness of satellite mission directly affects the efficacy of satellite. Aiming at the task process of optical reconnaissance satellite, detailed analysis of the relevant aspects of the task and established mathematical model. The simulation calculation of reconnaissance satellites' attitude adjustment time, transit time and data transmission time is carried out, and compared the relative difference of the multi-satellite to the specific observation task, effectively reflected the reconnaissance satellite mission efficacy, which provides a basis for the timeliness analysis and efficacy evaluation of optical reconnaissance satellite missions.

optical reconnaissance satellite；task process；timeliness of mission；efficacy evaluation

2017-05-14；

2017-05-26。

赵程亮(1991-)，男，河北衡水人，硕士研究生，主要从事天基信息支援方向的研究。

张占月(1973-)，男，河北吴桥人，硕士，教授，博士研究生导师，主要从事航天任务设计与分析方向的研究。

1671-4598(2017)12-0291-04

10.16526/j.cnki.11-4762/tp.2017.12.075

V474

A