视觉物质点跟踪方法在柔索模型验证中的应用

鄂薇，魏承,，谭春林，张大伟，赵阳

1.哈尔滨工业大学 航天学院，哈尔滨 150001 2.中国空间技术研究院 总体部，北京 100094

视觉物质点跟踪方法在柔索模型验证中的应用

鄂薇1，魏承1,*，谭春林2，张大伟2，赵阳1

1.哈尔滨工业大学 航天学院，哈尔滨 150001 2.中国空间技术研究院 总体部，北京 100094

空间柔性绳索在航天航空领域有着广泛的应用，柔性绳索具有结构大、刚度低、大变形的特t点，在做大范围运动时位移、转动与弹性变形相互耦合，增大了其动力学建模的难度。为验证柔性绳索动力学模型的准确性，采用非接触式的视觉测量方法进行实验验证，利用背景建模、差分、平滑与二值化一系列图像预处理方法提取绳索目标区域，并基于距离变换的多尺度连通骨架算法计算出绳索中心线，通过求解相机外参数矩阵计算出绳索中心线的平面位置。由于柔索自身灰度均匀，图像特征不明显，无法对绳索上特定位置进行跟踪，现有方法都在测量对象上粘贴或喷涂特征点，对于质量轻、弯曲刚度小的柔索，这种方法会影响柔索自身的动力学特性，因此提出一种适应绳索弯曲及纵向弹性形变的物质点跟踪算法，能够不借助外加特征的情况下，对绳索上任意给定物质点进行跟踪计算。以基于绝对节点坐标方法建立的柔索动力学模型为例验证其模型的准确性，结果表明，该绳索动力学模型仿真结果与实验结果具有较强的一致性。相比于其他测量方法，物质点跟踪算法能够降低柔索测量过程中的外干扰因素，为动力学模型验证提供准确的实验参考结果。

柔性绳索；物质点跟踪；动力学建模；绝对节点坐标；视觉测量

空间绳系结构在航天器轨道转移、在轨目标捕获、绳系卫星编队、绳系发电等空间任务中具有广阔的应用前景，在微重力环境中，绳系结构会产生横向振动、纵向振动、跳绳运动等，并且在空间展开、状态维持与回收时会发生复杂的动力学行为[1]。为解决上述问题需要建立能够准确描述绳系结构运动的动力学模型，但是对于大结构、低刚度、大变形的柔性绳索，基于小变形、小转动的传统建模方法已不满足其建模精度，而绝对节点坐标法[2-4]突破了有限元中对小变形、小转角的限制，适用于大变形的绳索动力学建模。

文献[5-13]都基于绝对节点坐标方法建立了索梁单元的动力学模型，但这些工作主要集中于数值仿真上，为了验证基于绝对节点坐标方法所建立的柔性绳索动力学准确性，需要采用实验手段进行验证，但是空间绳系结构属于柔性体，它在运动过程中会呈现出复杂的形态，传统的接触式测量法主要采用力传感器、电阻应变仪等，虽然可以得到某一点小变形的可靠数据，但对于绳索大变形、大范围运动不能有效测量，同时传统的接触式测量方法一般需要在绳索上安装传感器，会影响绳索本身的动力学特性，从而为空间绳系结构的测量增加了难度。

基于视觉的非接触式测量方法避免了在测量对象表面安装传感器的缺点,并且具有测量视场大、对测量环境要求较低等优点,在工程测量中有着广泛的应用前景,并正日益成为国内外研究热点。Irvine和Caughey[14]最早采用摄影方法对图像中绳索振动形态与动力学模型进行对比，没有量化绳索的运动速度与位移变化。Yoo等[15-17]利用单目相机测量柔性杆、薄片的大变形，通过在测量目标末端上粘贴反光特征点，能够测量出杆与薄片末端的大尺度振动的运动状态。Jung等[18]也利用单目相机测量柔性杆，但在杆上粘贴多个特征点，将所有特征点进行拟合描述整个臂杆的运动状态。Kawaguti等[19]利用双目相机测量柔性绳索，同样采取在绳上粘贴多个特征点的方式测量出柔性绳索的运动状态。以上方法都在测量目标上粘贴特征点，特征点是由反光材料制作的具有特殊形状的贴纸，虽然相对于传感器来说质量较轻，但对于质量轻、弯曲刚度小的柔索，尤其对于直径为0.5～2 mm的纤维绳，在表面上粘贴特征点会对目标的运动状态产生极大影响，无法测量出真实的运动状态。刘检华等[20-21]提出了一种基于中心线匹配法的双目视觉运动检测方法，该方法利用极线与绳索中心线进行相交来确定匹配点对，该方法能够在一定范围内测量出绳索的运动，但当绳索进行大范围运动中心线运动到与极线平行情况下，无法进行点对匹配。综上所述，单目测量与双目测量都有自身的局限性，由于本文的目标是验证动力学模型的准确性，能够约束绳索在平面范围内运动，因此采用单目视觉系统对绳索目标进行测量，避免双目视觉在绳索匹配过程中出现的错误，同时本文提出一种绳索物质点跟踪算法，能够在避免粘贴特征点的情况下实现对绳索上任意点运动状态的测量。

本文首先基于绝对节点坐标法建立绳索的动力学模型，根据该模型能够通过数值微分求解出绳索的运动状态，然后通过一系列的图像处理方法，提取出运动绳索的中心线，并求解相机外参数矩阵计算出绳索中心线的平面位置，进而提出物质点跟踪算法，能够避免在绳索上粘贴或喷涂特征的情况下跟踪绳索上任意点的运动状态，最后对基于绝对节点坐标法建立的柔索模型进行实验验证，分析模型建立的准确性与测量方法的可行性与合理性。

1 基于绝对节点坐标方法的绳索动力学模型

绝对节点坐标方法是Shabana于20世纪90年代提出的一种动力学建模方法[2]，主要用于解决大变形柔性体的动力学问题。柔性绳索结构长细比较大，其结构具有较强的变形能力，并且内部剪切效应几乎没有体现，根据Euler-Bernoulli梁理论建立动力学方程，将连续柔索离散为有限个横截面刚性无变形且始终与中心轴线垂直的一维两节点索梁单元。柔索的绕轴扭转影响也很小，可以进一步简化梁单元，仅考虑轴向拉伸和纯弯曲变形，在绝对参考系下的节点坐标作为广义变量建立动力学方程组[22]。

1.1 索梁单元位移场

图1显示了三维两节点索梁单元模型未变形与变形状态下的两种构型，绳索的运动与形变都以单元节点坐标进行描述[13]。

选取两端节点位移、位置梯度向量作为梁单元的广义坐标q，即

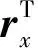
(1)

式中：L为梁单元长度;位置向量r由物质坐标的插值多项式表示为

(2)

图1 绝对节点坐标法索梁单元模型
Fig.1Absolute nodal coordinate formulation model of cable element

位置向量与广义节点坐标的关系为

r(x,t)=S(x)q(t)

(3)

其中，形函数可表示为

(4)

式中：ξ=x/L;I3为3阶单位矩阵。

1.2 索梁单元动能与质量矩阵

对单元内所有物质点的动能在体积上积分得到单元动能，沿索梁轴线上物质坐标的积分为

(5)

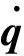
(6)

式中：绝对节点坐标方法得到的质量矩阵M为常数矩阵。

1.3 索梁单元应变能与广义弹性力

本文研究的索梁为理想的保守系统，应力应变仅与位置相关，与速度无关。索梁结构的变形程度由主轴应变ε与曲率κ进行描述，表达式为[7]

(7)

式中：ε为Green-Lagrange应变张量的第1个主对角线元素。轴向弯曲引起的应变由曲率表示，曲率表达式为

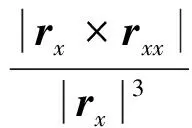
(8)

式中：rxx为位置向量对物质坐标的二阶导数。

根据应变能密度的体积积分计算轴向应变能Uel，可得：

(9)

式中：E为弹性模量。同理得到弯曲应变能为

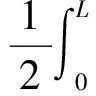
(10)

式中：I为梁横截面惯性矩。

总单元应变能为轴向、弯曲两部分之和，即

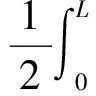
(11)

广义弹性力Qe为应变能对广义变量的偏导，轴向与弯曲广义弹性力Qel和Qet分别表示为

(12)

1.4 索梁单元空气阻力

在绳索的地面实验中，外力来源为重力与空气阻力，索梁单元受到的空气阻力为

(13)

式中：Ff为空气阻力；ρa为空气密度；CD为空气阻力系数；Sa为单元的受力面积；v为单元的运动速度。将空气阻力写成广义力Qf的形式为

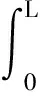
(14)

因此广义外力Qa可以写为

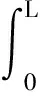
(15)

式中：Qg为重力的广义外力；Fg为重力。

综合以上内容，最终得到了绝对节点坐标系下的柔性绳索动力学模型为

(16)

2 单目视觉测量原理

2.1 坐标系定义

定义空间坐标系Owxwywzw，空间内任意一点在空间坐标系下表示为Pwi(xwi,ywi,zwi)，摄像机坐标系Ocxcyczc，Pwi在摄像机坐标系下表示为Pci(xci,yci,zci)，图像坐标系Oxy，Pwi投影到图像坐标系上的图像坐标为Pi(ui,vi)，如图2所示。

图2 视觉测量坐标系
Fig.2 Coordinates of visual measurement

空间坐标系与摄像机坐标系通过式(17)进行转换，摄像机坐标与图像坐标系通过式(18)进行转换。

(17)

(18)

式中：Mw为相机外参数矩阵；n=[nx,ny,nz]T、o=[ox,oy,oz]T与α=[αx,αy,αz]T分别为空间坐标系Owxwywzw中xw、yw、zw这3个轴在摄像机坐标系Ocxcyczc中的方向向量；p=[px,py,pz]T为空间坐标系Owxwywzw坐标原点在摄像机坐标系Ocxcyczc中的位置；Mi为相机内参数矩阵；kx和ky为等效焦距；u0和v0为相对于成像平面的主点坐标。

2.2 外参数矩阵求解

在相机内参数已经精确标定的情况下，给定图像中n个特征点的图像坐标以及相对应的空间坐标，能够求解出摄像机坐标系与空间坐标系之间的转换关系[23]，本文在绳索的运动平面上粘贴一张棋盘格标定板，共有位置已知的56个角点作为特征点，根据特征点计算出相机坐标与该平面坐标系之间的转换矩阵。

由于Pwi(i=1,2,…,n)在同一平面上时，其z轴值都为0，式(17)可以表示为

(19)

将式(19)代入到式(18)中可得

(20)

式中：x1ci=(ui-u0)/kx,y1ci=(vi-v0)/ky对于n个点可以得到n组如式(20)的方程组，整理为

A1H1+A2H2=0

(21)

式中：

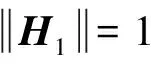
H2=[ox,oy,oz,px,py,pz]T

构造指标函数：

(22)

将式(21)的求解问题转换为优化问题，即在任意λ条件下保持指标函数F最小，能够得到H1和H2的优化解为

(23)

2.3 计算测量点平面坐标

该测量平面上的任意一点Pwi在测量平面上的齐次坐标可以表示为Pwi(xwi,ywi,zwi, 1)，其中zwi为已知量，该点与图像坐标系之间的投影关系为

(24)

式中：

si=m31xwi+m32ywi+m33zwi+m34

则

(25)

3 绳索物质点匹配与跟踪

在绳索运动过程中，能够通过一系列图像处理算法从单帧图像中提取出单像素宽度的绳索目标，从而根据2.3节内容计算出绳索的位置信息，但是在图像序列中，绳索上任意点的特征匹配却因为灰度均匀特征不明显而无法实现，而通过喷漆人工增加散斑的方法，对于半径为0.5～2 mm进行大范围运动的绳索也并不适用，从而无法实现在绳索上任意点的运动状态跟踪。因此提出一种物质点跟踪算法来实现对绳上任意点的跟踪。

3.1 绳索目标提取

运动绳索从图像序列中提取需要对图像进行一系列的预处理操作，将嘈杂的背景去除只在图像中保留绳索目标的图像，图像预处理包括背景建模、背景差分、图像平滑与图像二值化4个部分。首先采用平均背景法对背景进行建模，在对绳索运动之前对运动环境进行拍摄获取一定帧数的图像，将图像的均值作为背景模型；然后用式(26)将绳索运动的图像序列与背景模型进行差分获取前景图像。

(26)

式中：If(x,y)为差分后图像If像素坐标为(x,y)处的灰度值；Io(x,y)为原始图像Io像素坐标为(x,y)处的灰度值；Ib(x,y)为背景图像Ib像素坐标为(x,y)处的灰度值；g为图像灰度差分阈值。

差分后可以得到包含绳索以及一定噪声的粗糙前景图像，进而对前景图像进行平滑操作，本文采用窗口大小5×5，σ=1的高斯平滑算子来平滑图像，最后计算每张图像的Otsu最佳全局阈值，以该阈值对平滑后的图像进行二值化，得到只包含绳索目标的二值图像。

为展示绳索目标的图像提取过程，选取图像序列中的一帧进行计算，实验所用的软绳提取效果如图3所示。为清晰显示出绳索，将图像进行反色处理。

图3 绳索原始图像与二值化图像
Fig.3 Original image and binary image of cable

3.2 绳索中心线计算

图像提取后的绳索目标具有一定像素宽度，通常使用绳索的中心线对绳索进行等效，本文采用文献[24]中提出的基于距离变换的多尺度连通骨架算法来计算绳索的中心线，算法流程如下：

1) 对具有一定像素宽度的绳索二值图像进行距离变换，距离变换值为目标点到背景的最近距离。

2) 选择距离变换图中值最大的点作为种子点，以该点作为圆心，距离变换值作为半径对图像进行覆盖。

3) 覆盖后会产生n个连通域，n对应分支个数，找出距离新连通域最近的一点作为骨架延伸的候选点s，然后计算上一次前沿点8个邻域中与候选点s相邻的两点，计算这3点的下降梯度，选择下降梯度最缓慢的点作为新的延伸点。

对单像素宽度的绳索中心线进行链码标记，按照链码的顺序利用式(25)求解出每个像素点对应的平面坐标，检测像素点的斜率，将每条绳索链码中斜率相同的像素点去除，只保留关键节点，得到简化的绳索序列。由于链码是按照像素连通顺序进行标记的，其链码序列的最后一点为绳索末端点，检测每一帧图像中链码序列中最后一点，能够实现对绳索末端点运动轨迹的跟踪。图4为从初始时刻开始每隔84 ms所绘制的4条绳索完整位形图像，末端点用圆圈标记。

至此，能够获取整条绳索的位形，以及对绳索末端点的跟踪，但是在图像序列中无法对绳索上任意点进行一一对应，跟踪其运动状态。

图4 不同时刻绳索位形与末端点
Fig.4 Shape and endpoint of cable at different time

3.3 绳索物质点匹配算法

绳索在无受力情况下长度是固定值，在不考虑弹性形变时，绳索上的任意点距离绳索起始端的长度是不发生改变的，根据该原理通过判断长度能够跟踪绳索上任意点的运动状态。当考虑弹性形变时，在运动过程中绳索长度会伸长或缩短，假设这种长度的变化体现在绳索单元上是均匀的，因此当整条绳索从Lc0拉伸到Lc时，距离绳端为l的点会变成距离绳端为l(Lc/Lc0)，如图5所示。

图5 弹性形变下的绳索物质点匹配
Fig.5Cable element corresponding with elastic deformation

绳索物质点跟踪算法流程如下：

1) 在3.2节中已经计算出每一时刻绳索序列上的关键点，这些关键点按照顺序从绳索的起始端排列到绳索的末端点，将绳索点平面坐标表示为点集合{pci}(i=1,2,…,n)，并设置跟踪点距离绳端的长度l。

2) 利用式(27)将点集{pci}中所有点的间距累加，求解出当前时刻绳索的长度Lc，绳索在无弹性形变情况下的长度为Lc0，因此在当前时刻跟踪点距离绳端的长度l′=l(Lc/Lc0)。

(27)

3) 对点集{pci}从第1个点开始累加，直到累加到第j点，使

而第j+1点，使

此时所跟踪的点在pcj与pc(j+1)之间。

4) 利用式(28)计算出所跟踪点pt的平面坐标位置。

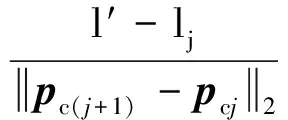
(28)

利用上述算法流程，能够跟踪到任意时刻在初始状态距离绳索端长度为l的点，获取其运动状态。

4 仿真与实验数据对比分析

4.1 视觉测量误差

实验选用德国AVT公司Manta-G223C CMOS传感器，图像采用帧频为119 frame/s，采集图像尺寸为544 pixel×1 024 pixel，测量对象是长为411 mm、直径为1 mm的凯夫拉纤维软绳，软绳一端固定在距离背景平面17 mm的位置，另一端由水平位置自由释放，软绳始终保持在黑色背景板范围内运动。

绳索运动的空间坐标系建立在背景板上，软绳的固定端为坐标系原点，沿重力方向为y轴，沿软绳水平释放方向为x轴，在背景板上粘贴棋盘格标定板，根据这些坐标已知的角点，能够计算出空间坐标系与相机坐标系之间的坐标转移矩阵Mw，如图6所示。

本实验的误差来源分为两个部分：一部分是采用56个空间位置已知的特征点来计算外参数矩阵Mw所产生的误差；另一部分是绳索中心线提取过程中产生的误差。

外参数矩阵是由背景板上提取的56个角点计算得来，这些角点的空间位置已知，但角点的坐标位置提取会存在误差，所计算出的外参数矩阵也会随之产生偏差。为验证平面测量的精度，采用实验背景板中56个已知空间位置的特征点进行计算，通过对真实值与测量值进行对比，可以得到平面测量的误差范围。测量偏差如图7所示，x方向的平均偏差为0.075 1 mm，最大偏差为0.265 4 mm，y方向的平均偏差为0.080 3 mm，最大偏差为0.246 5 mm。

图6 视觉测量设备
Fig.6 Experiment equipment of visual measurement

图7 平面位置测量偏差分布
Fig.7 Error distribution of position measurement

由于绳索中心线提取到的是单像素宽度的图像，当绳索真实中心线位于两个相邻像素之间时，所产生的误差最大，最大提取误差为±0.5 pixel。原坐标点(u,v)产生误差后的坐标点变为(u±0.5,v±0.5)，利用式(23)计算出该像素点空间位置的最大变换范围，作为图像提取产生的误差。通过计算得到x方向的平均偏差为0.487 9 mm，最大偏差为0.559 5 mm，y方向的平均偏差为0.477 3 mm，最大偏差为0.523 4 mm。

将两部分误差来源进行线性累加可得本实验测量误差x方向上的平均偏差为0.563 1 mm，最大偏差为0.824 9 mm，y方向上的平均偏差为0.557 6 mm，最大偏差为0.769 9 mm。

4.2 位形对比

实验帧频为119 frame/s，相当于仿真步长为8.4 ms，从绳索初始释放时刻，以84 ms为间隔取7个时刻，分别绘制仿真数据与视觉实验数据整条绳索的位形图像，如图8所示。从图中可以看出绳索的动力学仿真数据与实验数据基本吻合。

由于绳索的仿真单元与实验所测量绳索点尺度不同，不能直接量化出绳索仿真数据与实验数据之间的误差，因此取10 mm间隔作为单元点，利用物质点跟踪算法统一两组数据的单元尺度。并计算出在同一时刻整条绳索位形仿真数据与实验数据之间的差值，如表1所示。

结合图8和表1可以看出，仿真结果与实验结果之间整体趋势一致，在某些时刻差值较大，如t=168 ms时刻仿真与实验结果的差距较大，并且仿真模型中的绳索相对实验结果来说弯曲刚度较小。

图8 不同时刻绳索位形对比
Fig.8 Comparison of cable shape at different time

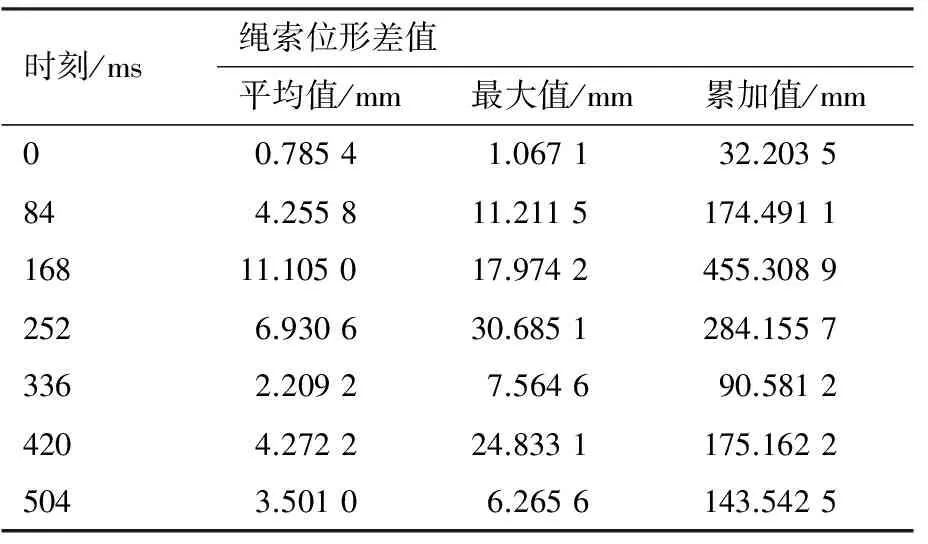
时刻/ms绳索位形差值平均值/mm最大值/mm累加值/mm00．78541．067132．2035844．255811．2115174．491116811．105017．9742455．30892526．930630．6851284．15573362．20927．564690．58124204．272224．8331175．16225043．50106．2656143．5425

4.3 不同物质点运动对比分析

选取距绳端不同距离的物质点进行跟踪，并将仿真数据与实验数据进行对比，图9与图10分别为l=200，300，411 mm的物质点在x轴与y轴方向的运动轨迹，其中l=411 mm的物质点也是实验绳索的末端点。

图9 绳索不同物质点在x轴方向的运动对比
Fig.9 Comparison of positions of different material points on cable in x axis direction

由于实验数据的时间步长是由相机硬件所确定，因此为了统一实验数据与仿真数据的步长，对实验数据进行插值，进而实现对仿真数据与实验数据之间的数据对比，并计算出所跟踪的3个点在连续时间段内仿真数据与实验数据之间的距离差，如表2所示。其中，平均相对误差与最大相对误差分别为平均误差与最大误差除以跟踪点距离固定端的长度。

图10 绳索不同物质点在y轴方向的运动对比
Fig.10 Comparison of positions of different material points on cable in y axis direction

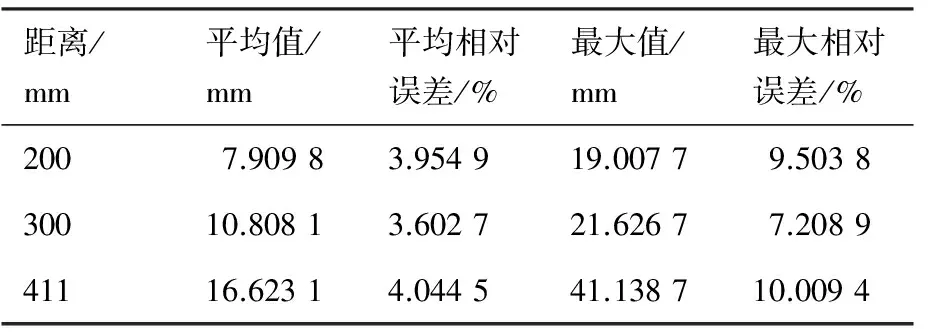
距离/mm平均值/mm平均相对误差/%最大值/mm最大相对误差/%2007．90983．954919．00779．503830010．80813．602721．62677．208941116．62314．044541．138710．0094

通过以上3个物质点视觉实验数据与模型仿真数据之间的对比结果，可以看出动力学模型仿真结果与实验结果具有一致性，距离绳索固定点位置越远的物质点误差越大，不同距离的跟踪点相对误差相近。通过实验对比分析，基于绝对节点坐标法建立的柔性绳索动力学模型能够描述绳索真实的运动状态，但是由于用梁单元等效编织绳的结构，忽略了编织绳内部相互耦合作用，还不能精准地描述真实绳索的运动状态，该模型与实验结果最大误差可以控制在10%以内。

5 结 论

1) 利用图像预处理算法提取绳索目标区域，并基于距离变换的多尺度连通骨架算法计算出绳索中心线，通过求解相机外参数矩阵计算出绳索中心线的平面位置，单目测量精度在x方向的平均偏差为0.563 1 mm，最大偏差为0.824 9 mm，y方向上的平均偏差为0.557 6 mm，最大偏差为0.769 9 mm。

2) 柔性绳索由于自身灰度均匀、图像特征不明显，为了避免在测量对象表面粘贴或喷涂特征点，影响柔索的动力学特性，提出适应绳索弯曲及纵向弹性形变的一种物质点跟踪算法，能够对绳索上任意给定点的运动状态进行跟踪。

3) 以基于绝对节点坐标法建立的绳索动力学模型为例，验证其模型准确性，通过仿真数据与实验数据的对比分析，模型仿真结果与实验结果具有较强的一致性，但由于忽略编织绳内部的耦合作用，还不能精准地描述真实绳索的运动状态，该模型与实验结果最大误差可以控制在10%以内。

[1] 金栋平, 文浩, 胡海岩. 绳索系统的建模、动力学和控制[J]. 力学进展, 2004(3): 304-313.

JIN D P, WEN H, HU H Y. Modeling, dynamics and control of cable system[J]. Advances in Mechanics, 2004(3): 304-313 (in Chinese).

[2] SHABANA A A. An absolute nodal coordinate formulation for the large rotation and large deformation analysis of flexible bodies: MBS96-1-UIC[R]. Chicago, IL: University of Illinois at Chicago, 1996.

[3] SHABANA A A. Definition of the slopes and the finite element absolute nodal coordinate formulation[J]. Multibody System Dynamics, 1997, 1(3): 339-348.

[4] SHABANA A A. Definition of ANCF finite elements[J]. Journal of Computational and Nonlinear Dynamics, 2015, 10(5): 054506.

[5] SHABANA A A, YAKOUB R Y. Three dimensional absolute nodal coordinate formulation for beam elements: Theory[J]. Journal of Mechanical Design, 2000, 123(4): 606-613.

[6] YAKOUB R Y, SHABANA A A. Three dimensional absolute nodal coordinate formulation for beam elements: Implementation and applications[J]. Journal of Mechanical Design, 2000, 123(4): 614-621.

[7] GERSTMAYR J, SHABANA A A. Analysis of thin beams and cables using the absolute nodal coordinate formulation[J]. Nonlinear Dynamics, 2006, 45(1-2): 109-130.

[8] 朱大鹏， 路英杰， 汤家力， 等. 大变形索梁单元在多体动力学框架下的应用[C]∥2007全国结构动力学学术研讨会论文集. 北京: 中国振动工程学会, 2007: 27.

ZHU D P, LU Y J, TANG J L, et al. Application of large deformation cable beam element in multibody dynamics[C]∥Proceedings of the 2007 National Symposium on Structural Dynamics. Beijing: Chinese Society for Vibration Engineering, 2007: 27 (in Chinese).

[9] DOMBROWSKI S V. Analysis of large flexible body deformation in multibody systems using absolute coordinates[J]. Multibody System Dynamics, 2002, 8(4): 409-432.

[10] LIU C, TIAN Q, HU H Y. New spatial curved beam and cylindrical shell elements of gradient-deficient absolute nodal coordinate formulation[J]. Nonlinear Dynamics, 2012, 70(3): 1903-1918.

[11] DMITROCHENKO O, MIKKOLA A. Digital nomenclature code for topology and kinematics of finite elements based on the absolute nodal coordinate formulation[J]. Journal of Multi-body Dynamics, 2011, 225(1): 34-51.

[12] 张越， 赵阳， 谭春林， 等. ANCF 索梁单元应变耦合问题与模型解耦[J]. 力学学报, 2016, 48(6): 1406-1415.

ZHANG Y, ZHAO Y, TAN C L, et al. The strain coupling problem and model decoupling of ANCF cable/beam element[J]. Chinese Journal of Theoretical and Applied Mechanics, 2016, 48(6): 1406-1415 (in Chinese).

[13] 张越， 魏承， 赵阳， 等. 基于ANCF 的松弛绳索动力学建模与仿真[J]. 航空学报, 2017, 38(4): 220586.

ZHANG Y, WEI C, ZHAO Y, et al. Dynamic modeling and simulation of slack rope based on absolute nodal coordinate formulation[J]. Acta Aeronautica et Astronautica Sinica, 2017, 38(4): 220586 (in Chinese).

[14] IRVINE H M, CAUGHEY T K. The linear theory of free vibrations of a suspended cable[J]. Proceedings of the Royal Society A, 1974, 341: 299-315.

[15] YOO W S, LEE J H, PARK S J, et al. Large oscillations of a thin cantilever beam: Physical experiments and simulation using the absolute nodal coordinate formulation[J]. Nonlinear Dynamics, 2003, 34(1): 3-29.

[16] YOO W S, LEE J H, PARK S J, et al. Large deflection analysis of a thin plate: Computer simulations and experiments[J]. Multibody System Dynamics, 2004, 11(2): 185-208.

[17] YOO W S, KIM M S, MUN S H, et al. Large displacement of beam with base motion: Flexible multibody simulations and experiments[J]. Computer Methods in Applied Mechanics & Engineering, 2006, 195(50): 7036-7051.

[18] JUNG S P, PARK T W, CHUNG W S. Dynamic analysis of rubber-like material using absolute nodal coordinate formulation based on the non-linear constitutive law[J]. Nonlinear Dynamics, 2011, 63(1-2): 149-157.

[19] KAWAGUTI K, TERUMICHI Y, TAKEHARA S, et al. The study of the tether motion with time-varying length using the absolute nodal coordinate formulation with multiple nonlinear time scales[J]. Journal of System Design and Dynamics, 2007, 1(3): 491-500.

[20] 王小寅, 刘检华, 宁汝新, 等. 一种基于双目视觉技术的运动线缆空间位姿测量方法[J]. 光学技术, 2010, 36(5): 725-729.

WANG X Y, LIU J H, NING R X, et al. Pose measurement method of motional cable harness based on binocular vision technology[J]. Optical Technique, 2010, 36(5):725-729 (in Chinese).

[21] 刘检华, 王小寅, 张天. 基于双目视觉的柔性线缆运动检测方法及误差分析[J]. 北京理工大学学报, 2012, 32(8): 795-800.

LIU J H, WANG X Y, ZHANG T. Motion detection method of flexible cable harness based on binocular vision and its error analysis[J]. Transactions of Beijing Institute of Technology, 2012, 32(8): 795-800 (in Chinese).

[22] 过佳雯. 大变形柔性多体系统高效数值计算方法研究[D]. 哈尔滨: 哈尔滨工业大学, 2016: 21-26.

GUO J W. Research on high efficient numerical algorithm of the flexible multibody dynamics with large deformation[D]. Harbin: Harbin Institute of Technology, 2016: 21-26 (in Chinese).

[23] 徐德, 谭民, 李原. 机器人视觉测量与控制[M]. 北京: 国防工业出版社, 2011: 35-40.

XU D, TAN M, LI Y. Robot vision measurement and control[M]. Beijing: National Defense Industry Press, 2011: 35-40 (in Chinese).

[24] 丁颐, 刘文予, 郑宇化. 基于距离变换的多尺度连通骨架算法[J]. 红外与毫米波学报, 2005, 24(4): 281-285.

DING Y, LIU W Y, ZHENG Y H. Hierarchical connected skeletonization algorithm based on distance transform[J]. Journal Infrared Millimeter & Waves, 2005, 24(4): 281-285 (in Chinese).

Verificationofflexiblecablemodelusingvisualmaterialpointtracking

EWei1,WEICheng1,*,TANChunlin2,ZHANGDawei2,ZHAOYang1

1.SchoolofAstronautics,HarbinInstituteofTechnology,Harbin150001，China2.InstituteofSpacecraftSystemEngineering,ChinaAcademyofSpaceTechnology,Beijing100094,China

Theflexiblecableiswidelyappliedinthefieldofastronauticsandaeronautics,andhasthecharacteristicsoflargestructure,lowrigidityandlargedeformation.Inlargerangemotion,thedisplacement,rotationandelasticdeformationoftheflexiblecablearecoupledwitheachother,increasingthedifficultiesindynamicmodelingoftheflexiblecable.Toverifytheaccuracyofthedynamicmodelfortheflexiblecable,thenon-contactvisualmeasurementmethodisused.Themovementareaofthecableisextractedbyaseriesofimagepreprocessingmethods,suchasbackgroundmodeling,andimagedifference,smoothingandbinarization.Thecablecenterlineisobtainedbythehierarchical-connectedskeletonizationalgorithmbasedondistancetransform,andtheplanerpositionofthecenterlineiscalculatedbysolvingthecameraexternalmatrix.Withevengraylevel,thecabledoesnothaveobviousimagecharacteristics,makingitdifficulttotrackaspecificpointofthecable.Inthepreviousmethods,thefeaturepointonthecableispastedorsprayed,affectingthedynamiccharacteristicsoftheflexiblecable.Amaterialpointtrackingalgorithmwhichcanadapttothebendingandlongitudinalelasticdeformationoftheflexiblecableisproposed.Thealgorithmcanbeusedtotrackanypointofthecablewithoutadditionalfeatures.Thedynamicmodelfortheflexiblecableisbuiltbasedontheabsolutenodalcoordinateformulation,andthesimulationresultsareconsistentwiththeexperimentalresults.Comparedwithothermeasurementmethods,thematerialpointtrackingalgorithmcanreducethefactorsofexternalinterferenceinthemeasurementprocess,providingaccurateexperimentalreferenceresultsfordynamicmodelverification.

flexiblecable；materialpointtracking；dynamicsmodeling;absolutenodalcoordinate;visualmeasurement

2017-04-18；

2017-06-13；

2017-07-04；Publishedonline2017-07-232103

URL：http://hkxb.buaa.edu.cn/CN/html/20171219.html

s：NationalBasicResearchProgramofChina(2013CB73004)；NationalNaturalScienceFoundationofChina(11772102)

.E-mailweicheng@hit.edu.cn

http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn

10.7527/S1000-6893.2017.221334

2017-04-18；退修日期2017-06-13；录用日期2017-07-04；网络出版时间2017-07-232103

http://hkxb.buaa.edu.cn/CN/html/20171219.html

国家“973”计划(2013CB73004)；国家自然科学基金(11772102)

.E-mailweicheng@hit.edu.cn

鄂薇，魏承，谭春林,等．视觉物质点跟踪方法在柔索模型验证中的应用J． 航空学报,2017,38(12):221334.EW,WEIC,TANCL,etal.VerificationofflexiblecablemodelusingvisualmaterialpointtrackingJ.ActaAeronauticaetAstronauticaSinica,2017,38(12):221334.

V414.3；TP391.41

A

1000-6893(2017)12-221334-11

徐晓)