空间太阳能电站重力姿态-轨道-结构耦合特性

刘玉亮，邬树楠，刘家夫，吴志刚,

1.大连理工大学 航空航天学院，大连 116024 2.大连理工大学 工业装备结构分析国家重点实验室，大连 116024 3.沈阳航空航天大学 航空航天工程学部，沈阳 110136

空间太阳能电站重力姿态-轨道-结构耦合特性

刘玉亮1,2，邬树楠1,2，刘家夫3，吴志刚1,2,*

1.大连理工大学 航空航天学院，大连 116024 2.大连理工大学 工业装备结构分析国家重点实验室，大连 116024 3.沈阳航空航天大学 航空航天工程学部，沈阳 110136

基于结构小变形假设，将太阳帆塔式空间太阳能电站(SSPS)简化为两端自由的Euler-Bernoulli梁模型，并建立在重力作用下，假设只考虑轨道平面内电站的姿态和轨道运动与结构振动的耦合动力学方程。其受到的重力、重力梯度力矩和广义重力将以其结构尺寸与运行轨道半径的比值为变量进行泰勒展开，并保留至四阶项。通过对其动力学方程的分析发现，当假设只考虑轨道平面内的姿态运动和轨道平面内结构的横向振动时，结构振动对姿态和轨道运动的影响只存在于三阶及其以上的重力和重力梯度力矩中。此外，在重力激励下当电站的结构角频率小于某一特定值时，其结构振动将会出现屈曲不稳定的现象。保证电站结构振动稳定的条件也将在文中给出。为了分析重力激励对结构振动的影响，提出了“等效角频率”的概念。数值仿真表明，当电站结构角频率较低时，重力激励将对电站的振动产生很大影响。而且重力引起的姿态-轨道-结构的耦合作用也将对空间太阳能电站的轨道运动产生较大影响，轨道半径误差能达千米量级。

空间太阳能电站；姿态-轨道耦合；结构振动；重力梯度；泰勒展开

空间太阳能电站(SSPS)的概念由美国科学家Glaser博士于1968年提出[1]。自从这一概念提出以来，多个航天大国陆续开展了相关研究，并提出了多种概念设计，如美国国家航空航天局的“ALPHA”构型[2]，日本宇航开发局的绳系构型[3]，欧洲太空局的太阳帆塔式构型[4]，以及中国空间技术研究院侯欣宾等提出的多旋转关节式构型[5]和西安电子科技大学段宝岩院士等提出的“OMEGA”式构型[6]。迄今为止，世界各国一共提出了20多种SSPS方案[7]。

在目前关于SSPS的研究中，大都集中在对概念设计的研究，而对其在轨运行过程中的轨道、姿态与结构动力学行为的研究较少。为保证SSPS的正常工作，首先需要清楚地了解其在轨动力学行为。Graf, Jr[8]首先分析了SSPS运行在地球静止轨道上的轨道动力学特性。McNally等[9]提出了一种新颖的SSPS运行轨道——地球同步拉普拉斯轨道，并指出了这种轨道相对于地球静止轨道的优势。刘玉亮等[10]对该种轨道的动力学特性进行了进一步的分析,提出了评价SSPS轨道的指标。McNally等[11]进一步研究了运行在地球同步拉普拉斯轨道的SSPS在无控状态下的姿态运动。Wie和Roithmayr[12]初步分析了地球静止轨道“Abacus”式SSPS的轨道和姿态运动特性，并设计了轨道保持控制器和对日指向控制器。Ishimura等[13-14]通过建立起绳系SSPS的有限元模型，综合分析了在地球引力场中其轨道运动、姿态运动及结构振动的稳定性问题。Glaese和McDonald[15]基于多体动力学的理论建立了“ISC”式SSPS的轨道和姿态运动及结构振动的动力学模型，并设计了太阳指向控制器。周荻和范继祥[16]针对绳系SSPS大角度机动时产生的振动问题进行了研究，提出了一种主动振动控制系统。魏乙等[17]通过采用绝对节点坐标法建立起了绳系SSPS在轨运行中轨道、姿态和结构振动的耦合动力学方程，并对其动力学特性进行了分析。

在上述关于SSPS姿态和轨道运动和结构振动的研究中，大都没考虑三者之间的相互耦合作用[8-12,15,17]；其轨道运动常被假设为开普勒轨道，而姿态运动和结构振动与轨道运动之间的耦合作用常忽略不计。传统卫星因具有较小尺寸和较高结构频率的特点，这种假设是合理的。但对于空间太阳能电站这种超大、超柔的空间结构而言，它们之间的耦合作用需要重新考虑。此外，有学者采用有限元方法综合分析了SSPS轨道、姿态和结构振动的动力学特性，但并没有揭示它们之间的耦合机理[13-14,16]。

目前，在关于航天器姿态运动和轨道运动耦合作用的研究中，很多学者已取得了一些优异的成果。Duboshin[18]首先推导了两个任意形状天体在相互引力作用下的姿态和轨道耦合运动的微分方程。Lange[19]研究了一种任意构型的航天器在地球引力场中的姿态和轨道耦合运动，并将其所受到的重力和重力梯度力矩通过Taylor级数进行展开，保留至ε2项(ε=ρ/R,ρ为航天器的特征尺寸，R为航天器的运行轨道半径)，为姿态和轨道耦合运动的数值运算提供了一种方法。Sincarsin和Hughes[20]研究了一种超大型的板状航天器在地球引力场中的姿态和轨道耦合运动，并将其所受到的重力和重力梯度力矩保留至ε4项。Ashenberg[21]研究了两个任意形状且相互吸引的天体之间的姿态和轨道耦合问题，并提出了高阶惯性积的概念。通过采用Ashenberg提出的方法，Wang和Xu[22]分析了一种特殊构型的航天器在某一小行星表面运动时的姿态和轨道耦合特性。基于上述研究成果，刘玉亮等[23-24]研究了太阳帆塔式SSPS在地球引力场中的姿态和轨道耦合问题。然而，在这些研究中，大都将航天器或者天体当成刚体来处理，并未考虑柔性振动所带来的影响。对于SSPS这种超柔的航天器而言，这种假设是不合理的，因此需要重新考虑柔性振动给SSPS姿态和轨道耦合运动带来的影响。

为了解决上述问题，本文将重点研究太阳帆塔式空间太阳能电站(见图1)在地球引力场作用下的姿态-轨道-结构耦合作用,并揭示它们之间的耦合机理。全文安排如下：第1节，将对坐标系和符号进行定义并推导出SSPS在轨运行过程中的轨道运动、姿态运动和结构振动的动力学方程。第2节，将SSPS受到的重力、重力梯度力矩和广义重力进行泰勒展开，并保留至四阶项，同时对其动力学方程进行分析，给出“等效角频率”的定义。第3节，通过数值仿真对姿态-轨道-结构耦合的动力学特性进行分析。结论将在第4节给出。

图1 太阳帆塔式空间太阳能电站
Fig.1 Sun tower space solar power station

1 动力学方程

1.1 坐标系与假设

为了便于描述SSPS的运动，本节将给出坐标系和一些符号的定义，如图2和图3所示。由于太阳帆塔式SSPS的宽度h远小于其长度l，如图1所示，故在本文中，太阳帆塔式SSPS被简化成一个两端自由的Euler-Bernoulli梁模型[24]，SSPS的结构振动假设只考虑垂直于太阳能电池板表面方向的横向振动，且假设只考虑SSPS轨道平面内的姿态运动和结构振动，即垂直于太阳能电池板表面方向的结构横向振动在SSPS的轨道平面内。

图2 坐标系示意图
Fig.2 Schematic of coordinate systems

图3 太阳帆塔式SSPS在轨示意图
Fig.3 Schematic of sun tower SSPS in the Earth’s orbit

1.2 动力学方程

在本文中，SSPS的变形被假设为小变形，可通过模态坐标表示，则u可表示为

(1)

式中：Ai(t)为第i阶模态的模态坐标；φi(x)为第i阶归一化的模态振型，且满足式(2)所示条件[26]。

(2a)

(2b)

(2c)

式中：δij为Kronecker符号；Mii为第i阶模态的广义质量，对于归一化的振型φi(x)，Mii≡1 kg。

单位质量dm相对于惯性系Oei1j1的绝对加速度在浮动坐标系Oi2j2下的分量可表示为

ω×(ω×ρb)]dm=L(qb)+fgdm

(3a)

dm=σdx

(3b)

沿SSPS的长度方向对式(3a)进行积分，并结合式(2a)和式(3b)对方程进行化简，可得到SSPS的轨道运动方程为

(4)

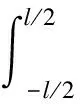
(5)

(6)

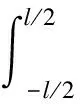
(7)

2 重力、重力梯度力矩和广义重力

为便于进行数值计算，需要得到式(4)、式(5)和式(7)右端项的显式表达式。在本节中，将会对SSPS在轨运行过程中受到的重力、重力梯度力矩及广义重力进行推导。

在本文中，地球被假设成一个均匀的球体，不考虑地球扁率带来的影响，则SSPS单位质量受到的重力可表示为

(8)

式中：μ为地球引力常数；r=rb，且可表示为

(9)

将式(9)通过泰勒级数进行展开，保留至(ρb/R)4，并将其代入式(8)可得

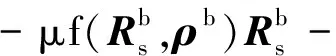
(10a)

(10b)

(10c)

(11)

式中：i≠j且I1=Jxx。由式(2a)、式(2b)、式(2c)和O作为SSPS的质心可知，式(12)所示条件得以满足。

Jx=Jxxx=Jφi=Jx φi=Jφiφj=0

(12)

此外，对于两端自由的Euler-Bernoulli梁而言，其横向振动的各阶归一化振型可表示为

(13)

Jxxφe=Jxφoφo=Jxφeφe=Jxxxφo=

Jxxφeφo=Jxxxxφe=Jxxxφoφo=Jxxxφeφe=0

(14)

从附录中式(A1)～式(A3)可以看出，当假设只考虑轨道平面内的姿态运动和结构振动时，且结构振动假设只考虑垂直于太阳能电池板表面方向的横向振动，太阳帆塔式SSPS的结构振动对其受到的重力和重力梯度力矩的影响存在于三阶及其以上的重力和重力梯度力矩中，对低阶重力和重力梯度力矩则无影响。此外，不同的姿态角下，SSPS受到的二阶及其以上的重力和一阶及其以上的广义重力的大小不同；而且，在不同的轨道半径下，SSPS受到的各阶重力梯度力矩和广义重力的大小也不同，故SSPS的轨道运动、姿态运动和结构振动之间存在着耦合关系。

将式(A3)代入式(7)，并结合式(14)可得

(15)

(16)

(17)

(18)

(19)

3 仿真与分析

为了分析SSPS在轨运行中，其结构的“等效角频率”随姿态角的变化规律和各阶重力、重力梯度力矩及广义重力对其轨道运动、姿态运动和结构振动的影响。本节将给出两个数值仿真算例。

图4 一阶临界角频率的平方随θ的变化 Fig.4 Variation of squared value of the first ordercritical angular frequency ()2 with θ

图5 不同一阶角频率下F随θ的变化
Fig.5Charts of F change over θ with different first order angular frequencies

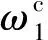
表1给出了采用不同模型计算时所考虑的重力、重力梯度力矩及广义重力。

表1不同阶次模型的重力、重力梯度力矩和广义重力

Table1Gravitationalforces,torquesandgeneralizedforcesofdifferentordermodels

ModelForceTorqueGeneralizedforce(i=1，2)NMF0g0FOMEig1SOMF0g，F2gT2gEig1，Eig2TOMF0g，F2g，F3gT2g，T3gEig1，Eig2，Eig3FOMF0g，F2g，F3g，F4gT2g，T3g，T4gEig1，Eig2，Eig3，Eig4

Notes:NM——None higher orders Model; FOM, SOM, TOM, and FOM represent the First, Second, Third, and Fourth order Models, respectively

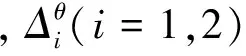
图6 不同阶次的重力对轨道运动的影响
Fig.6 Influences of different order gravitational forces on orbital motion

图7 不同阶次的重力梯度力矩对姿态运动的影响
Fig.7 Influences of different order gravitational gradient torques on attitude motion

图8 不同阶次的广义重力对结构振动的影响
Fig.8 Influences of different order generalized gravitational forces on structural vibration

4 结 论

1) 对于假设只考虑轨道平面内的姿态运动和轨道平面内结构横向振动的两端自由的梁式空间太阳能电站，其结构振动对姿轨运动的影响只存在于三阶及其以上的重力和重力梯度力矩中，其影响可忽略不计。

2) 在一定姿态角和重力激励下，当空间太阳能电站的结构角频率低于某一值时，其结构将出现屈曲不稳定，其主要原因是由于结构因形变产生的回复力小于结构受到的重力梯度力引起的。此外，当结构的角频率靠近临界角频率时，重力激励将对其结构振动产生较大影响，且主要由前两阶广义重力引起。

3) 空间太阳能电站的姿态-轨道-结构耦合作用将对电站的轨道运动产生较大影响，能使其轨道半径误差达至千米量级，且主要由二阶重力引起。此外，对其姿态运动也将产生一定影响，姿态角误差将随时间逐渐积累。

[1] GLASER P E. Power from the sun: Its future[J]. Science, 1968, 162(3856): 857-861.

[2] MANKINS J, KAYA N, VASILE M. SPS-ALPHA: The first practical solar power satellite via arbitrarily large phased array: AIAA-2012-3978[R]. Reston, VA: AIAA, 2012.

[3] SASAKI S, TANAKA K, HIGUCHI K, et al. A new concept of solar power satellite: Tethered-SPS[J]. Acta Astronautica, 2007, 60(3): 153-165.

[4] SEBOLDT W, KLIMKE M, LEIPOLD M, et al. European sail tower SPS concept[J]. Acta Astronautica, 2001, 48(5): 785-792.

[5] 侯欣宾, 王立, 张兴华, 等. 多旋转关节空间太阳能电站概念方案设计[J]. 宇航学报, 2015, 36(11): 1332-1338.

HOU X B, WANG L, ZHANG X H, et al. Concept design on multi-rotary joints SPS[J]. Journal of Astronautics, 2015, 36(11): 1332-1338 (in Chinese).

[6] YANG Y, ZHANG Y Q, DUAN B Y, et al. A novel design project for space solar power station (SSPS-OMEGA)[J]. Acta Astronautica, 2016, 121: 51-58.

[7] 王立， 侯欣宾. 空间太阳能电站的关键技术及发展建议[J]. 航天器环境工程, 2014, 31(4): 343-350.

WANG L, HOU X B. Key technologies and some suggestions for the development of space solar power station[J]. Spacecraft Environment Engineering, 2014, 31(4): 343-350 (in Chinese).

[8] GRAF O F, Jr. Orbital motion of the solar power satellite: NASA-CP-151603[R]. Washington, D.C.: NASA, 1978.

[9] MCNALLY I, SCHEERES D, RADICE G. Locating large solar power satellites in the geosynchronous Laplace plane[J]. Journal of Guidance, Control, and Dynamics, 2015, 38(3): 489-505.

[10] 刘玉亮, 邬树楠, 吴志刚, 等. 空间太阳能电站地球同步拉普拉斯轨道动力学特性[J]. 中国空间科学技术, 2016, 36(5): 1-8.

LIU Y L, WU S N, WU Z G, et al. Dynamic characteristics of geosynchronous Laplace orbit for space solar power station[J]. Chinese Space Science and Technology, 2016, 36(5): 1-8 (in Chinese).

[11] MCNALLY I, SCHEERES D, RADICE G. Attitude dynamics of large geosynchronous solar power satellites[C]∥AIAA/AAS Astrodynamics Specialist Conference. Reston, VA: AIAA, 2014: 1-13.

[12] WIE B, ROITHMAYR C M. Attitude and orbit control of a very large geostationary solar power satellite[J]. Journal of Guidance, Control, and Dynamics, 2005, 28(3): 439-451.

[13] ISHIMURA K, NATORI M, WADA M. Stability analysis and decentralized system design of large space structures based on potential field[C]∥13th International Conferenc on Adaptive Structures and Technologies. Boca Raton, FL: CRC Press, 2003: 413-422.

[14] ISHIMURA K, HIGUCHI K. Coupling between structural deformation and attitude motion of large planar space structures suspended by multi-tethers[J]. Acta Astronautica, 2007, 60(8): 691-710.

[15] GLAESE J R, MCDONALD E J. Space solar power multi-body dynamics and controls, concepts for the integrated symmetrical concentrator configuration: TCD20000222A[R]. Washington, D.C.: NASA, 2000.

[16] 周荻, 范继祥. 绳系太阳能发电卫星姿态机动的主动振动控制[J]. 宇航学报, 2012, 33(5): 605-611.

ZHOU D, FAN J X. Boundary control in the attitude maneuvering of tethered space solar power satellite[J]. Journal of Astronautics, 2012, 33(5): 605-611 (in Chinese).

[17] 魏乙, 邓子辰, 李庆军, 等. 绳系空间太阳能电站动力学响应分析[J]. 宇航学报, 2016, 37(9): 1041-1048.

WEI Y, DENG Z C, LI Q J, et al. Analysis of dynamic response of tethered space solar power station[J]. Journal of Astronautics, 2016, 37(9): 1041-1048 (in Chinese).

[18] DUBOSHIN G N. The differential equations of translational-rotational motion of mutally attracting rigid bodies[J]. Soviet Astronomy, 1958, 2: 239-250.

[19] LANGE B. Linear coupling between orbital and attitude motions of a rigid body[J]. Journal of the Astronautical Sciences, 1970, 18: 150-167.

[20] SINCARSIN G B, HUGHES P C. Gravitational orbit-attitude coupling for very large spacecraft[J]. Celestial Mechanics, 1983, 31(2): 143-161.

[21] ASHENBERG J. Mutual gravitational potential and torque of solid bodies via inertia integrals[J]. Celestial Mechanics and Dynamical Astronomy, 2007, 99(2): 149-159.

[22] WANG Y, XU S. Gravitational orbit-rotation coupling of a rigid satellite around a spheroid planet[J]. Journal of Aerospace Engineering, 2012, 27(1): 140-150.

[23] 吴志刚, 刘玉亮, 张开明, 等. 高阶重力和力矩对空间太阳能电站运动的影响[J]. 空间控制技术与应用, 2016, 42(4): 1-5.

WU Z G, LIU Y L, ZHANG K M, et al. The influences of higher order gravitational force and torque to the motion of space solar power station[J]. Aerospace Control and Application, 2016, 42(4): 1-5 (in Chinese).

[24] LIU Y L, WU S N, ZHANG K G, et al. Gravitational orbit-attitude coupling dynamics of a large solar power satellite[J]. Aerospace Science and Technology, 2017, 62: 46-54.

[25] 刘暾， 赵钧. 空间飞行器动力学[M]. 哈尔滨： 哈尔滨工业大学出版社， 2003: 153-154.

LIU D, ZHAO J. Dynamics of spacecraft[M]. Harbin: Harbin Institute of Technology Press, 2003: 153-154 (in Chinese).

[26] ASHLEY H. Observations on the dynamic behavior of large flexible bodies in orbit[J]. AIAA Journal, 1967, 5(3): 460-469.

[27] BAINUM P M, KUMAR V K, JAMES P K. The dynamics and control of large flexible space structures, Part B: Development of continuum model and computer simulation: NASA-CR-l63612[R]. Washington,D.C.: NASA, 1978.

[28] KANE T R, RYAN R, BANERJEE A K. Dynamics of a cantilever beam attached to a moving base[J]. Journal of Guidance, Control, and Dynamics, 1987, 10(2): 139-151.

[29] 杨辉, 洪嘉振, 余征跃. 两种刚柔耦合动力学模型的对比研究[J]. 上海交通大学学报, 2002, 36(11): 1591-1595.

YANG H, HONG J Z, YU Z Y. Study on two dynamic models for a rigid-flexible coupling system[J]. Journal of Shanghai Jiaotong University, 2002, 36(11): 1591-1595 (in Chinese).

[30] ASHLEY H. Observations on the dynamic behavior of large flexible bodies in orbit[J]. AIAA Journal, 1967, 5(3): 460-469.

附录A

(A1)

式中：

(A2)

式中：

(A3)

其中：

其中：

(A4)

Gravitationalattitude-orbit-structurecouplingofspacesolarpowerstation

LIUYuliang1, 2,WUShu’nan1, 2,LIUJiafu3,WUZhigang1, 2, *

1.SchoolofAeronauticsandAstronautics,DalianUniversityofTechnology,Dalian116024,China2.StateKeyLaboratoryofStructuralAnalysisforIndustrialEquipment,DalianUniversityofTechnology,Dalian116024,China3.DepartmentofAerospaceEngineering,ShenyangAerospaceUniversity,Shenyang110136,China

Basedontheassumptionofsmalldeformationofthestructure,thesuntowerSpaceSolarPowerStation(SSPS)issimplifiedtoaEuler-Bernoullibeamwithbothendsbeingfree,andthecoupleddynamicalequationsfortheorbitalandattitudemotionsandstructurevibrationofthestationundertheexcitationofgravitationalforceareproposed,whichconsideronlytheattitudemotionandthestructurevibrationontheorbitalplane.Thegravitationalforce,torqueandgeneralizedforceareexpandedinaTaylorseriesinthesmallratio(spacecraftsize/orbitalradius)whichpermitstermsuptofourthordertoberetained.Ananalysisofthestructuralvibrationequationsfindsthattheinfluenceofstructuralvibrationontheorbitalandattitudemotionexistsonlyinnolessthanthree-ordergravitationalforcesandtorquesifonlyattitudemotionandtransversevibrationofthestructureontheorbitalplaneareconsidered.Inaddition,abucklinginstabilityofthestructurecanoccurundertheexcitationofgravitationalforceiftheangularfrequencyofthespacesolarpowerstationisbelowacertainthreshold.Theconditiontoguaranteethestabilizationofthestructurevibrationisalsoderived.Aconceptof“equivalentangularfrequency”isdefinedforanalyzingtheinfluenceoftheexcitationofgravitationalforceonstructuralvibration.Numericalsimulationsshowthattheinfluenceoftheexcitationofgravitationalforceonthestructuralvibrationisgreatiftheangularfrequencyislow.Thecouplingeffectamongtheorbitalandattitudemotionandstructuralvibrationonorbitalmotionisalsogreat,andtheerroroftheorbitalradiuscanreachtheorderofonekilometer.

spacesolarpowerstation;attitude-orbitcoupling;structuralvibration;gravitygradient;Taylorexpansion

2017-03-15；

2017-04-17；

2017-05-17；Publishedonline2017-12-071001

URL：http://hkxb.buaa.edu.cn/CN/html/20171215.html

s：NationalNaturalScienceFoundationofChina(11432010,11502040);theFundamentalResearchFundsfortheCentralUniversities(DUT15LK31)

.E-mailwuzhg@dlut.edu.cn

http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn

10.7527/S1000-6893.2017.221244

2017-03-15；退修日期2017-04-17；录用日期2017-05-17；网络出版时间2017-12-071001

http://hkxb.buaa.edu.cn/CN/html/20171215.html

国家自然科学基金(11432010,1150240); 中央高校基本科研业务费专项资金(DUT15LK31)

.E-mailwuzhg@dlut.edu.cn

刘玉亮，邬树楠，刘家夫，等. 空间太阳能电站重力姿态-轨道-结构耦合特性J. 航空学报，2017,38(12):221244.LIUYL,WUSN,LIUJF,etal.Gravitationalattitude-orbit-structurecouplingofspacesolarpowerstationJ.ActaAeronauticaetAstronauticaSinica,2017,38(12):221244.

V412

A

1000-6893(2017)12-221244-12

徐晓)