三阶两点边值问题正解的存在性
庄国华
(江苏联合职业技术学院 南京分院,江苏 南京 210019)
三阶两点边值问题正解的存在性
庄国华
(江苏联合职业技术学院 南京分院,江苏 南京 210019)
本文研究一类非线性三阶两点点边值问题:正解的存在性,其中f:[0,+∞)→[0,+∞)连续,a:(0,1)→[0,+∞)连续且满足允许a(t)在t=0或者t=1处奇异。通过利用锥上的不动点的定理得到上述边值问题正解的存在性结果。
锥;格林函数;正解;边值问题
三阶微分方程在应用数学和物理等很多科学领域中有着广泛的应用背景和重要的理论价值,因此三阶边值问题受到了众多学者的广泛关注,见文献[1-15]。在[3]中作者考虑了三阶三点边值问题:
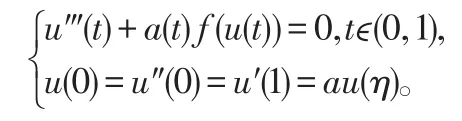

通过不动点指数理论得到上述边值问题至少一个正解的存在性条件。
受以上文献的启发,本文研究如下一类三阶两点边值

解的存在性。
在本文中,假设以下条件成立:
(C1):f:[0,+∞)→[0,+∞)连续;
(C2):a:(0,1)→[0,+∞)连续,a(t)在(0,1)上不恒为 0,且
1 引理和定义
引理1[4]若e(t)ϵC[0,1],则边值问题:

引理2[4]G(t,s)具有如下性质:对于任意的(t,s)ϵ[0,1]×[0,1],有

引理3[4,5]令0<τ<1,则边值问题(1)的唯一解u(t)≥0,且满足:
引理4[16]设E是一个Banach空间,P是E中的锥,假设 Ω1,Ω2是 E 中满足的两个开子集,且是一个全连续算子,满足:(i)‖Tu‖≤‖u‖,uϵP∩∂Ω1,且 ‖Tu‖≥‖u‖,uϵP∩∂Ω2;或 者(ii)‖Tu‖≤‖u‖,uϵP∩∂Ω1,且则 T 在中至少有一个不动点。
2 主要结果
定义算子:

定 理 1假设(C1)、(C2)成立,如果f0=0,f∞=∞(超线性),则边值问题(1)至少存在一个正解。
证明考虑空间X={uϵC[0,1]:u(t)≥0,tϵ[0,1]},赋予范数则显然X是一个Banach空间。对于任意0<τ<1,定义锥:显然,K⊂X。

由引理2,可知

所以,有

对任意的 (t,s)ϵ[τ,1]×[0,1],由引理 2 和(5)可得:

表明TK⊂K。容易验证:T:K→K是全连续的,且算子T的不动点即为边值问题(1)的正解。
因为f0=0,则存在R1>0,当 0≤u≤R1时,有f(u)≤εu成立,其中ε>0且满足:

当uϵK,‖u‖=R1时,由引理 2 和(6)可知:

令 Ω1={u∈K:‖u‖<R1},由(7)可知‖Tu‖≤‖u‖,u∈K⋂∂Ω1。
另一方面,由f∞=∞ 可知,存在R2>R1,使得当时,有f(u)≥λu成立,其中λ>0满足:

令 Ω2={u∈K:‖u‖<R2},则u∈K,‖u‖=R2时,有从而由(8)可得:
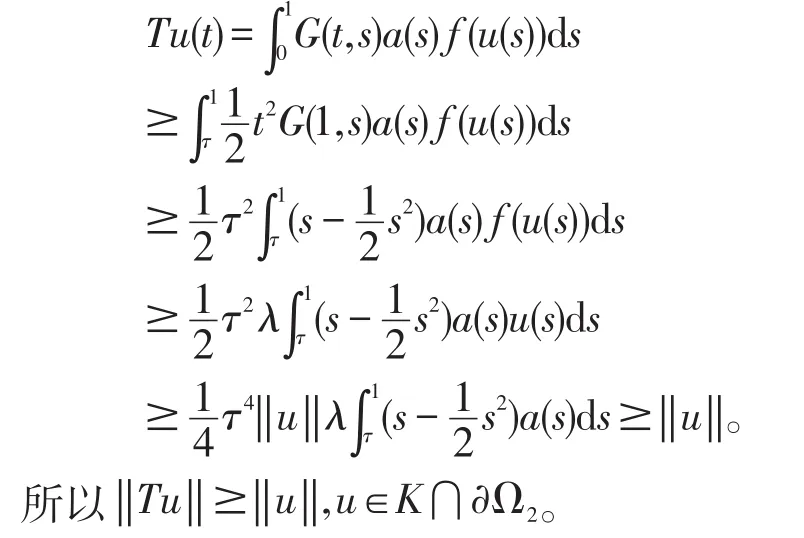
由引理 4知算子有一个不动点u0∈K⋂即边值问题(1)至少存在一个正解。
定理 2假设(C1)、(C2)成立,如果f0=∞,f∞=0(次线性),则边值问题(1)至少存在一个正解。
证明因为f0=∞,在存在R3>0,使得当0≤u≤R3时有f(u)≥γu成立,其中γ>0满足:
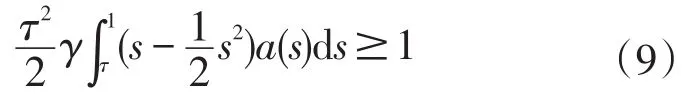
则当u∈K,‖u‖=R3时,由引理 2和(9)可知:

令 Ω3={uϵK:[u]<R3},由(10)可知‖Tu‖≥‖u‖,uϵK∩ ∂Ω3。
因为f∞=0,则存在R>0,使得当u≥R时,有f(u)≤μu,其中μ>0,且满足:

下面分成两种情况考虑:
(1)若果f是有界的,即当u∈[0,+∞)时,有f(u)≤M成立。此时令

使得当u∈K,‖u‖=R4时,对任意t∈[0,1]有

(2)若果f是无界的,令R4=max{2R3,R},使得

当u∈K,‖u‖=R4时,由(11)和(12)可知

因此,无论f是上述的哪种情况,都可以令Ω4={u∈K:‖u‖<R4},从而对任意uϵK∩∂Ω4的,都有‖Tu‖≤‖u‖成立。进而由引理4可知边值问题(1)至少存在一个正解。
[1]吴红萍.一类三阶三点非齐次边值问题的两个正解[J].西北师范大学学报(自然科学版),2012,48(6):9-12.
[2]郭丽君.三阶三点边值问题正解的存在性[J].兰州文理学院学报(自然科学版),2016,30(1):1-5.
[3]Sun J P,Guo L J,Peng J G.Multiple non-decreasing positive solutions for a singular third order three pointbvp[J].Communications in Applied Analysis,2008,12:91-100.
[4]Li S H.Positive solutions of nonlinear singular thirdorder two-point boundary value problem[J].Journal of Mathematical?Analysis?and Applications,2006,323:413-425.
[5]刘瑞宽.一类奇异三阶两点边值问题正解的存在性[J].四川师范大学学报(自然科学版),2014,37(4):482-485.
[6]武 晨.非线性二阶三点边值问题正解的存在性和唯一性[J].淮阴师范学院学报(自然科学版),2015,14(4):288-290.
[7]程德胜,武 晨.一类三阶三点边值问题正解的存在性[J].华侨大学学报(自然科学版),2017,38(1):127-130.
[8]武 晨.一类三阶边值问题正解的存在性和唯一性[J].南通大学学报(自然科学版),2017,16(2):87-89.
[9]张长沐.三阶微分方程三点边值问题正解的存在性[J].山东师范大学学报(自然科学版),2017,32(2):30-34.
[10]孙建平,杨雪梅,赵亚红.非线性三阶三点边值问题系统的正解[J].兰州理工大学学报,2017,43(4):150-153.
[11]郭丽君.非线性微分方程三阶三点边值问题正解的存在性[J].山东大学学报(理学版),2016,51(12):47-53.
[12]孙建平,张小丽.非线性三阶三点边值问题正解的存在性[J].西北师范大学学报(自然科学版),2014,48(3):29-31.
[13]吴红萍.一类非线性三阶三点边值问题的多个正解[J].贵州大学学报(自然科学版),2014,31(2):4-6.
[14]高永馨,汪凤琴.三阶非线性微分方程三点边值问题解的存在性[J].黑龙江大学自然科学学报,2015,32(4):421-427.
[15]裴明鹤.三阶非线性常微分方程两点与三点边值问题解的存在性与唯一性[J].北华大学学报(自然科学版),2003,4(1):5-11.
[16]郭大钧.非线性泛函分析[M].济南:山东科学技术出版社,2005:289-332.
Existence of positive solution for a third-order twopointboundary value problems
ZHUANG Guo-hua
(Branch of Nanjing,Jiangsu Union Technical Institute,Nanjing Jiangsu210019,China)
This paper studied the existence of positive solution to the following third-order two-point boundary value prob-,wheref:[0,+∞)→[0,+∞),a:(0,1)→[0,+∞)are continuous,anda(t)may be singular att=0ort=1.The proof of the main results is based on the fixed-point on cone.
cone;Green function;positive solution;boundary value problem
O175.8文献识别码:A
1004-4329(2017)04-012-03
10.14096/j.cnki.cn34-1069/n/1004-4329(2017)04-012-03
2017-10-10
江苏省教育科学“十三五”规划课题(B-b/2016/03/55)资助。
庄国华(1981- ),男,硕士,讲师,研究方向:微分方程边值问题。

