不同磁控溅射模式的膜厚均匀性仿真计算研究
张 赛,易文杰,袁卫华,彭立波,孙雪平
(中国电子科技集团公司第四十八研究所,湖南 长沙 410111)
不同磁控溅射模式的膜厚均匀性仿真计算研究
张 赛,易文杰,袁卫华,彭立波,孙雪平
(中国电子科技集团公司第四十八研究所,湖南 长沙 410111)
根据溅射余弦分布理论建立了平行溅射和斜溅射模型,计算了矩形磁控靶溅射和圆形磁控靶溅射的膜厚均匀性;讨论了各种溅射模式的膜厚均匀性趋势和优劣,为磁控溅射系统的设计布局提供了支撑。
矩形靶;圆形靶;平行溅射;斜溅射
薄膜膜厚均匀性是衡量薄膜质量和镀膜装置性能的一项重要指标,任何一种有实际应用价值的薄膜,都对膜厚分布有特定的要求。除了少数特殊场合外,绝大多数情况下,都要求镀膜面内膜厚尽可能均匀一致,即要求有尽可能好的膜厚均匀性,对这个问题的研究有很重要的实际意义。提高膜厚均匀性有多种方法,比如将源放置在合适的位置,采用旋转基片,增加遮挡机构等[1,2]。对于磁控溅射镀膜,由于阴极靶面电磁场的非均匀分布,造成等离子体密度的分布不均,最终导致靶原子的不均匀溅射和不均匀沉积。磁控溅射的膜厚均匀性,除了上述几种方法之外,还可以通过改进磁路布置,优化靶基距等措施来提高。对于一台特定的磁控溅射镀膜设备,阴极靶的形状、磁路等结构参数及基片的运动方式已经确定,难以改变。相比之下,基片比较容易放置在靶前的不同位置。随着基片和溅射靶相对位置的变化,膜厚分布也会发生变化。有必要寻找出最佳的靶基距,以获取最佳的膜厚均匀性,许多研究人员曾经对磁控溅射的膜厚均匀性进行过讨论[3-5],这些研究者详细地讨论了溅射系统的几何参数、夹具转动方式等对薄膜厚度分布的影响,他们假设整个磁控靶是均匀刻蚀,或者是靶的环形跑道是均匀刻蚀。而实际上,由于磁控溅射靶面不同位置电磁场变化很大,从而导致环形跑道区内不同位置的刻蚀速率的变化也相当大,刻蚀速率并非均匀,而是服从一定的分布[6]。有很多研究人员研究了靶基距等参数对膜厚均匀性的影响[7-10]。同时,溅射系统结构参数在设计时考虑膜厚均匀性会大大提升设备的性能。针对以上问题,本文根据溅射余弦理论上建立了溅射系统模型,根据靶面刻蚀的实际情况建立了刻蚀速率方程,利用MATLAB语言编写了计算程序,分别对矩形平面靶平行溅射、圆形平面靶平行溅射和圆形平面靶斜溅射等3种模式下的膜厚均匀性进行了计算,讨论了靶基距、扫描距离、偏心距离和倾斜角度等参数对均匀性的影响。
1 基本理论与模型
磁控溅射的工作气体一般是Ar,溅射时的真空度在1.0 Pa左右,溅射出来的粒子在到达基片之前会受到气体分子的多次碰撞。由于溅射粒子的能量是气体分子能量的4个数量级以上,因此可以认为这种碰撞不会改变溅射粒子的运动方向,溅射粒子的分布仍然服从余弦分布[11]。
设P为基片面上任一点,ds为P点的微小面元。Q为靶面上一点,dσ为Q点的微小面元。单位时间内,dσ小面元在ds上沉积的薄膜厚度可以表示为:

其中,m是单位时间内dσ溅射出镀膜材料的总质量,θ是膜料分子对沉积面元ds的入射角,即ds法线与入射原子方向的夹角,φ是溅射原子的发射角,ρ0是靶材的密度。r是溅射面元和沉积面元之间的距离,即P、Q两点的间距。
1.1 靶平面与基片平面平行
平行磁控溅射示意图如图1所示。图中靶平面与基片平面的距离为h,基片平面X'Y'上点的坐标为(x',y'),靶平面 XY 上点的坐标为(x,y)。由图中的几何关系可以得到P、Q两点的间距:

式(1)表示了小面元dσ在基片面元ds上沉积的薄膜厚度,整个靶面在基片平面上P点形成的膜厚为:

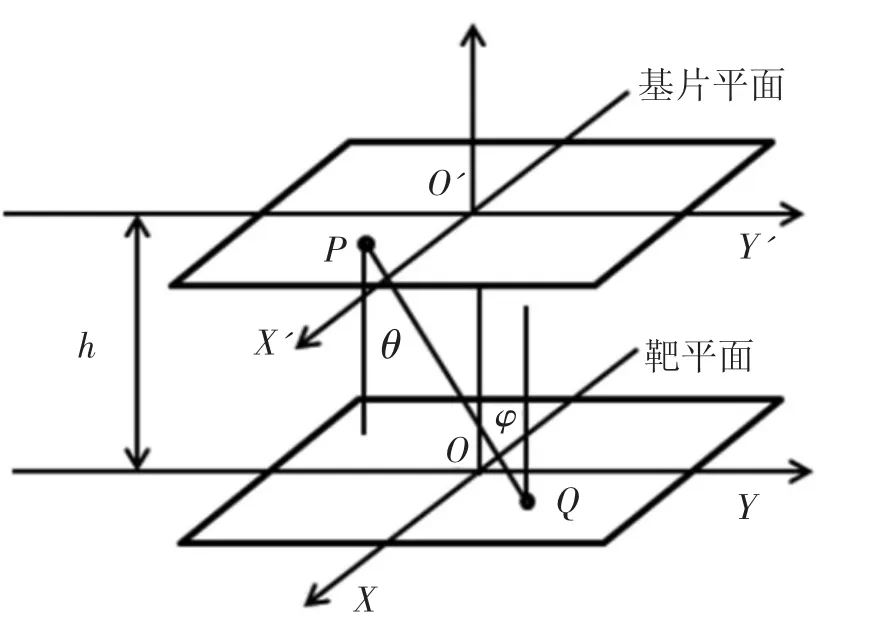
图1 靶与基片相对位置示意图
1.2 靶平面与基片平面之间的夹角为α
靶平面与基片平面之间存在夹角,通常是用在圆形靶对圆形基片斜溅射镀膜的情况,因此两平面示意图简化为如图2所示,靶坐标系中Q点的坐标为(x,y,z),基片坐标系中的 P 点得坐标为(x',y',z'),基片平面坐标系原点在靶平面坐标系中的坐标为(X,Y,Z),设X=0。由图中的几何关系可以得到,在靶坐标系中坐标为(x,y,z)的 Q 点转换到基片坐标系中的坐标为:

由公式(4)可以得到P、Q两点的间距


式 (1)表示了小面元dσ在基片面元ds上沉积的薄膜厚度,整个靶面在基片平面上P点形成的膜厚为:
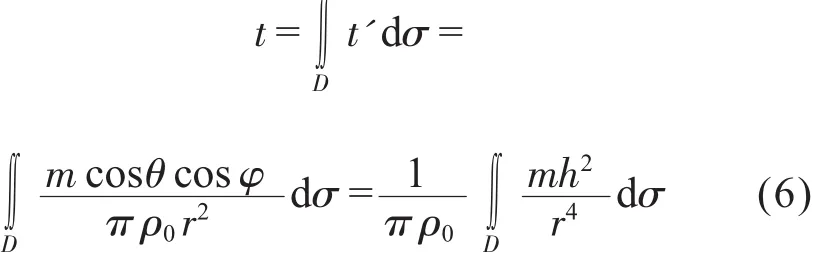
其中:

1.3 刻蚀速率函数
为了较准确的反映溅射过程,把刻蚀速率看作一个函数来处理。图3表示工作一定时间后,靶面实际的刻蚀情况。可以看出,刻蚀基本在跑道内进行,而且跑道的中心具有最大的刻蚀深度,表明该点得刻蚀速率最大,单位时间内溅射出的靶材质量最大。
根据图3靶面位置与刻蚀深度的关系,进行曲线拟合,确定线性刻蚀速率函数的斜率为0.5。由于靶面上不同的小面元在相同时间里溅射出靶材的质量m不同,因此,m是位置(x,y,z)的函数,在数值上等于该点的刻蚀速率(溅射速率)与时间的乘积。从公式(3)和公式(6)可以看出,只要知道磁控溅射阴极靶的基本结构和靶面的刻蚀情况就可以计算出薄膜的相对分布。

图3 实测靶面位置与刻蚀深度的关系
2 计算结果与分析讨论
2.1 矩形平面磁控靶平行溅射
靶面的刻蚀只在跑道区进行,对矩形平面磁控溅射靶,可将积分区D简化为两个条形刻蚀槽和两个半圆环刻蚀槽,其尺寸和结构如图4所示。在徐均琪的计算中,阴极靶面的尺寸为480 mm×80 mm,溅射跑道区2L=200 mm,R1=10 mm,R2=30 mm。图5给出的是不同靶基距(h)下X轴向薄膜相对厚度分布,可以看出与文献的计算结果一致。图6给出的整个基片面(120 mm×120 mm)范围不同靶基距下薄膜相对厚度分布,薄膜相对厚度是该点处厚度与整个范围内厚度最大值的比值。图 6(a)是 h=25 mm、(b)是 h=50 mm、(c)是h=100 mm、(d)是h=150 mm的膜厚分布图,从图中可以看出,随着靶基距的增加,膜厚均匀性越好,且在Y方向的均匀性较X方向的均匀性好。因此基片在Y方向尺寸增加不会改变破坏薄膜的膜厚均匀性,特别是对于小尺寸的样品,可以在Y方向适当增加数量。
中国电子科技集团公司第四十八研究所的JST-100型磁控溅射镀膜机,阴极靶面的尺寸为432 mm×76 mm,溅射跑道区2L=360 mm,R1=10 mm,R2=30 mm,基片盘的尺寸为300 mm×300 mm,靶基距h=100 mm。图7是整个基片盘范围内薄膜的相对厚度分布图,相对厚度的最小值为0.129 8,根据薄膜膜厚均匀性的计算公式f=此时均匀性f=74.9%。

图4 矩形平面磁控靶溅射跑道的简化图
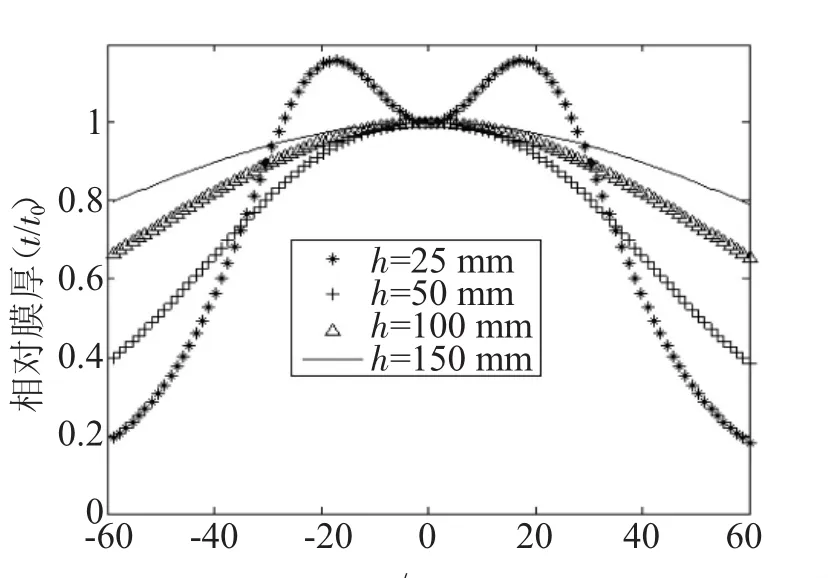
图5 不同靶基距(h)下X轴向薄膜相对厚度分布

图6 不同靶基距下薄膜相对厚度分布
JST-100型磁控溅射镀膜机的基片盘在X方向增加了扫描功能,从-Y轴观察的扫描示意图如图8所示(本文中使用右手坐标系),基片盘在X方向做水平匀速扫描运动。图9为不同扫描距离SM时基片盘上薄膜的膜厚均匀性,可以看出随着扫描距离SM的增加,均匀性越好。当SM=188.1 mm时,基片盘处于过扫描的边界,此时薄膜的膜厚均匀性f=23.15%。
SM=238.1 mm时,即基片盘过扫描50 mm,不同靶基距h时基片盘中心轴线薄膜的膜厚均匀性如图10所示。从图中可以看出,靶基距h<75 mm时,均匀性满足<5%。实际工艺结果的膜厚均匀性<4%,通过增加挡板机构,均匀性<3%。
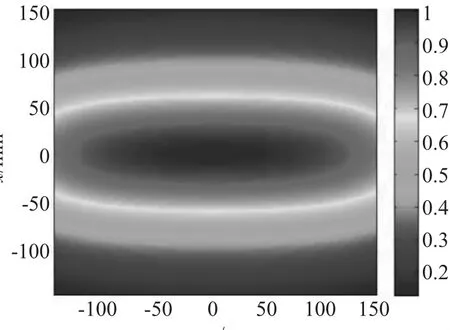
图7 基片盘范围(300 mm×300 mm)内薄膜的相对厚度分布图
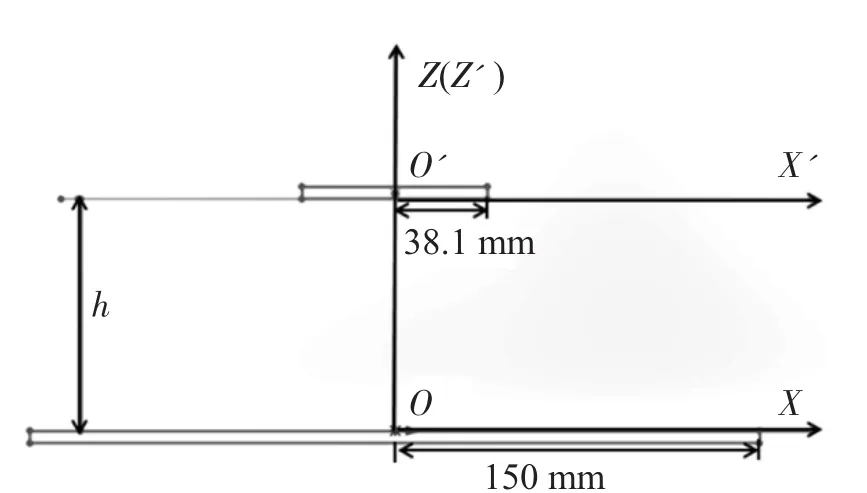
图8 扫描示意图
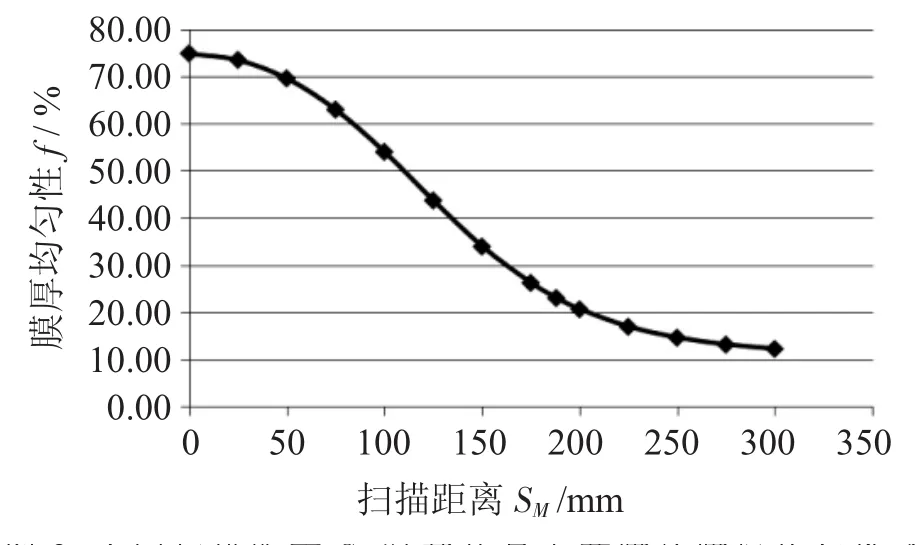
图9 不同扫描距离SM时基片盘上薄膜的膜厚均匀性f

图10 不同靶基距h时基片盘中心轴线薄膜的膜厚均匀性f
2.2 圆形平面磁控靶平行溅射
使用100 mm(4英寸)的圆形平面磁控靶平行溅射,基片中心与靶中心连线与靶面垂直,使用200 mm(8英寸)基片来讨论薄膜的均匀性。不同靶基距h时的薄膜相对厚度如图11所示,靶中心与基片中心重合,基片的薄膜厚度是轴对称的,半径R上的薄膜厚度代表整个圆基片的薄膜厚度。从图中可以看出,随着靶基距的增加,薄膜的相对厚度差值越小,代表均匀性越好;基片尺寸的减小,也能比较明显地提高薄膜的均匀性;基片的尺寸越大,靶基距对薄膜的均匀性影响越显著。靶基距200 mm时,100 mm(4英寸)靶镀 150 mm(6英寸)基片的均匀性约10%,100 mm(4英寸)基片的均匀性约5%。100 mm(4英寸)靶镀50 mm(2英寸)基片时,薄膜的均匀性可以很好的控制在3%左右。

图11 不同靶基距h时的薄膜相对厚度
基片中心与靶中心不重合时,为了达到基片成膜厚度轴对称的目的,基片需绕自己的中心轴旋转,基片中心与靶中心的距离设为X。靶基距h=100 mm时,不同X值的薄膜相对厚度如图12所示。从图中可以看出,平行溅射时,偏心距离的增大会显著的改变基片上的薄膜膜厚均匀性,在X=100 mm时均匀性在5%以内,但是此时靶的中心已处于基片盘的边缘,在实际工艺时,此时的靶材利用率会很低。因此在膜厚均匀性与靶材利用率之间存在一个平衡关系,高的均匀性时靶材利用率低,高靶材利用率时均匀性差。

图12 h=100 mm时,不同X值的薄膜相对厚度
靶基距h=200 mm时,不同X值的薄膜相对厚度如图13所示。从图13也可以看出,偏心距离的增加可以有效地改善薄膜的均匀性,同样存在靶材利用率与均匀性的矛盾问题。比较图12和图13,可以发现靶基距h的增加能够很好地改善薄膜的均匀性,这一点与图10的矩形靶均匀性规律是不同的。

图13 h=200 mm时,不同X值的薄膜相对厚度
2.3 圆形平面磁控靶斜溅射
为解决靶材利用率与高均匀性之间的矛盾,出现了倾斜溅射的设计与布局方式。基片与靶的相对位置如图14所示,靶基距h是靶中心与基片中心的垂直距离,靶的倾斜角为α,靶坐标系原点O'在平面坐标系 OXYZ中的坐标为(X,Y,Z),其中Y=0,Z=h。R是基片的半径,基片绕Z轴旋转。表1为靶基距h=100 mm时不同偏心距离X和不同倾斜角α的膜厚均匀性,靶为100 mm(4英寸)圆形,基片为200 mm(8英寸)圆形。

图14 圆形平面磁控靶斜溅射时基片与靶的相对位置示意图
从表1中可以发现,此时的膜厚均匀性没有线性规律,不同的偏心距离X和不同的倾斜角度α需要计算才能得到大致的膜厚均匀性数值。从表中数据可以看出,靶基距h=100 mm时,偏心与倾斜溅射配合并不能很好地改善薄膜的均匀性,均匀性的最小值为7.27%,并不能满足<5%的要求。
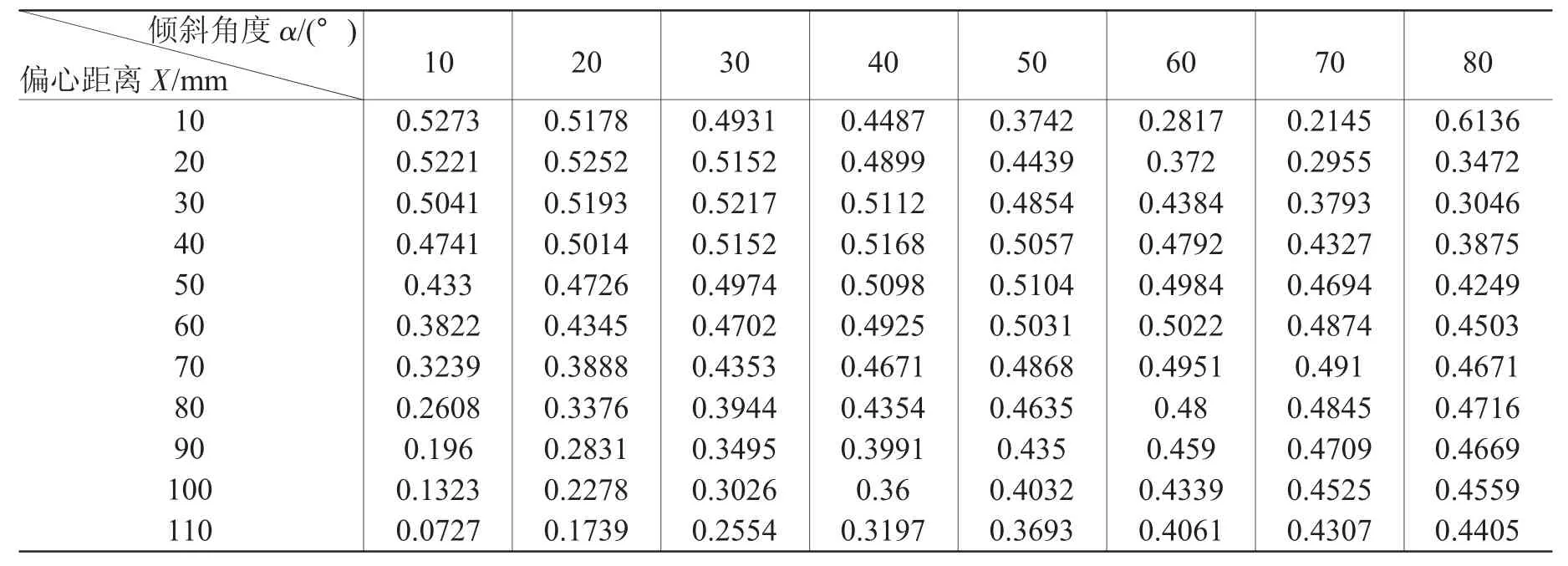
表1 靶基距h=100 mm时,不同偏心距离X和不同倾斜角度α的膜厚均匀性
表2为靶基距h=200 mm时不同偏心距离X和不同倾斜角度α的膜厚均匀性。从表中的数据可以发现,此时的膜厚均匀性同样没有线性规律。X=10 mm、α=50°时和 X=70 mm、α=70°时,膜厚均匀性都<2%,能够比较轻松的找到膜厚均匀性很好的布局方式。均匀性较好的布局都存在着倾斜角度或偏心距离的问题,同样会有大量的靶材未沉积到基片上。
中国电子科技集团公司第四十八研究的M79100-1/U型磁控溅射镀膜机,是3个50 mm(2英寸)靶斜溅射镀1个100 mm(4英寸)基片,使用本方法计算的膜厚均匀性是4.02%,实际工艺的膜厚均匀性<3%。圆形靶斜溅射能够带来很好的膜厚均匀性,同时这种布局方式可以很轻松地实现多个靶的共溅射,在靶材不昂贵的情况下是一种很好的设计方式。

表2 靶基距h=200 mm时,不同偏心距离X和不同倾斜角度α的膜厚均匀性
3 结 论
通过对磁控溅射靶的详细测量,根据溅射余弦分布理论和计算薄膜厚度的积分函数,开发了磁控溅射靶平行溅射和斜溅射的计算模型,编制了计算程序,得到了以下结论:
(1)对于矩形磁控靶平行溅射,基片上沿靶长度方向的均匀性优于宽度方向,膜厚均匀性主要由靶宽度方向的均匀性决定;随着靶基距的增加,膜厚均匀性变好。此结论与文献[7]的计算结果一致。同时,给出了成熟磁控溅射机台整个基片盘的膜厚均匀性,随着靶基距的增加,有扫描功能的均匀性反而会变差。
(2)圆形平面磁控靶平行溅射,随着靶基距的增加,薄膜的均匀性越好;基片尺寸的减小,也能比较明显的提高薄膜的均匀性;基片的尺寸越大,靶基距对薄膜的均匀性影响越显著。此时,膜厚均匀性与靶材利用率之间存在一个平衡关系,高的均匀性时靶材利用率低,高靶材利用率时均匀性差。同时,靶基距的增加能够很好地改善薄膜的均匀性,与矩形靶的平面扫描溅射相反。
(3)圆形平面磁控靶斜溅射,在大的靶基距和大的倾斜角度情况下,可以得到很好的膜厚均匀性,这种方式可以很方便的实现不同靶的共溅。
(4)为了在较小靶基距情况下得到较好的膜厚均匀性,以后将设计多跑道的磁控溅射靶,根据需要来调节各处的磁场形状和强度。同时,本文提到了靶材的利用率问题,将根据靶面刻蚀情况和布局方式来综合计算靶材的实际有效利用率。
[1]严一心,林鸿海.薄膜技术[M].北京:兵器工业出版社,1994.87-95.
[2]Hou Q R,Gao J.Influence of a magnetic field on deposition of diamond-like carbon films[J].Applied Physics A,1998,(67):417-420.
[3]胡作启,李佐宜,缪向水,等.磁控溅射薄膜的膜厚均匀性理论研究[J].华中理工大学学报,1996,24(1):89-92.
[4]Swann S.Flim Thickness Distribution in Magnetron Sputtering[J].Vaccum,1988,38(8~10):791-794.
[5]T Yamazaki,N Ikeda.Uniformity of sputtered films fromed by fan-shaped composite targets[J].Thin Solid Films,1992,(209):76-180.
[6]T Fukami,F Shintani,M Naoe.Observations on the operation of a planar magnetron sputtering system by target erosion patterns[J].Thin Flims,1987,(151):373-381.
[7]徐均琪,易红伟,蔡长龙,等.磁控溅射膜厚均匀性与靶 -基距关系的研究[J].真空,2004,(2):25-28.
[8]高士铁.小靶大基片多工位磁控溅射镀膜膜厚均匀性研究[D].沈阳:东北大学,2010.
[9]康莹.直流磁控溅射离子镀镀层膜厚均匀性表征及研究[D].西安:西安理工大学,2013.
[10]张以忱,高士铁,陈旺.小圆平面靶磁控溅射镀膜均匀性研究[J].真空,2010,47(2):21-26.
[11]范正修,薛松生.磁控溅射薄膜的厚度分布[J].应用科学学报,1993,11(2):136~139.
The Simulation Study of Thickness Uniformity of Films Deposited by Different Magnetron Sputtering Methods
ZHANG Sai,YI Wenjie,YUAN Weihua,PENG Libo,SUN Xueping
(The 48thResearch Institute of CETC,Changsha 410111,China)
The paralell sputtering and oblique sputtering models built up on cosine distributted theory are used to calculate the thickness uniformity of films deposited with rectanglar magnetron sputtering and circular magnetron sputtering.To aid the design and regulation of magnetron sputtering systems,the trend of thickness uniformity of films deposited with different magnetron sputtering methods as well as the advantages and disadvantages of different magnetron sputtering methods are then analyzed and discussed.
Rectangular target;Circular target;Paralell sputtering;Oblique sputtering
TN305.92
A
1004-4507(2017)06-0010-07
2017-09-21
湖南省自然科学基金资助项目(14JJ2142)
张赛(1986-),男,山西芮城人,硕士,工程师,主要从事半导体设备的研发和工艺开发。

