桥墩概化方法对水动力数学模型计算结果的影响研究
辛小康
(长江水资源保护科学研究所,武汉 430051)
桥墩概化方法对水动力数学模型计算结果的影响研究
辛小康
(长江水资源保护科学研究所,武汉 430051)
为分析平面二维数学模型中不同桥墩概化方法对防洪评价结果的影响,借助于MIKE 21水动力模型,以长江宜昌江段某桥梁工程为例,分三种不同的桥墩概化方法计算了桥墩对百年一遇洪水位、行洪流速的影响。结果表明:三种概化方法反映出来的影响规律基本一致,桥墩上游水位增加、流速减小;桥墩所在断面水位增加,流速增加;桥墩挡水面以下河段流速减小,挡水面以外河道两侧行洪流量增加,流速增加。但采用网格地形高程修正法得出的计算结果更为合理,考虑到数学模型计算稳定性需要,推荐使用网格地形修正和糙率修正相结合的方法。
水动力;数学模型;概化方法;洪水影响评价
我国现行的 《中华人民共和国防洪法》《河道管理范围内建设项目管理的有关规定》等法律法规,要求在河道管理范围内建设桥梁、码头等对河道行洪具有影响的建设项目必须进行防洪评价[1]。根据 《洪水影响评价报告编制导则》(SL520-2014)》,对壅水影响范围较大或影响较为严重的建设项目,宜采用数学模型计算或物理模型试验的方法开展论证。随着计算机技术的快速发展,水动力数学模型被越来越多地应用到建设项目防洪影响评价工作。
跨河桥梁工程是目前较为普遍的涉水工程之一,桥梁工程的桥墩在河道中占用一定的行洪面积,对河道行洪产生影响。特别是对于一些中小型河流而言,桥墩宽度与河道宽度的比例较大,需要借助于水动力数学模型开展相对精确的计算与分析。李磊等[2]采用一维数学模型研究了桥梁对河道行洪的影响,张细兵等[3]、陈绪坚等[4]采用二维数学模型研究了桥梁工程对河道水流流量的影响,张小峰等[5]采用三维数学模型研究了桥墩附近的水流结构。一般而言,在开展防洪影响评价时,采用平面二维水流数学模型对桥墩用水及局部流速的影响进行计算。
桥墩建成以后,主要是改变了河道地形高程,但由于数学模型计算网格的精度问题,在开展模型计算时,不同的技术工作者对桥墩的概化处理方式不同,从而会得出稍有区别的计算结果。王晨阳等[6]采用加密网格的方法概化桥墩,一般适用于桥墩尺寸较大的情形。张细兵等[3]采用局部糙率修正的方法概化桥墩,附加糙率的确定往往比较困难。曹民雄等[7]采用局部地形高程修正的方法概化桥墩,比较接近于实际情况,但会影响模型计算稳定。本文采用丹麦水力学研究所开发的MIKE 21水动力 (FM)模块,分析不用桥墩概化方法对水动力数学模型计算结果的影响,为实际工作中选择合适的概化方法提供技术支撑。
1 模型方法与案例
1.1 模型控制方程
MIKE 21水动力 (FM)模块控制方程由描述水流运动的连续性方程和动量方程组成,模型控制方程如下:

式中:η为水面高程,h为总水深,g为重力加速度,ρ为水的密度,ρ0为 (淡)水的参考密度。f=2ΩsinΦ为科氏力系数 (Ω为旋转角速率,Φ为地理纬度),Pa为大气压强,Sij为辐射应力张量。S和 (us,vs)分别为点源的排放量和速度。u和v为流速在深度上的平均值;(τsx,τsy)和 (τbx,τby)为水面风应力张量和河床床面应力张量,河床床面应力与糙率参数n值有关。Tij为侧向应力。
1.2 模型求解方法
目前无论是描述水动力过程的浅水方程组,还是描述物质输运的对流扩散方程,都无法通过传统的经典数学方法求其理论解。因此,目前广泛采用数值方法求得其近似解。对于浅水方程组,MIKE 21 FM采用有限体积法进行离散和求解,采用Riemann近似解计算网格单元的对流通量,采用Roe格式估算网格单元交界面的附加变量,通过采用具有二阶精度线性梯度重构技术离散方法分析[3]。
1.3 研究对象
本研究以长江中游宜昌江段为计算案例,计算范围为宜昌磨盘溪至云池共计约12 km的长江干流江段。该江段磨盘溪下游2.5 km处建设了某高速路桥跨越长江,该桥梁有6处桥墩位于长江河道,桥墩为圆柱型,直径6 m,桥墩对长江干流水动力产生影响,模型计算范围见图1,MIKE 21 FM模块的计算网格见图2。

图1 长江宜昌江段水质数学模型计算范围示意图Fig.1 Sketch of computing range for water quality model in Yichang section

图2 桥墩所在河段水质数学模型计算网格示意图Fig.2 Sketch of computing grid of river section with bridge pier
2 桥墩概化方法
2.1 局部网格地形高程修正法
所谓局部地形修正法是指通过区别工程前后工况桥墩所在模型计算网格单元内的河底高程来反映桥墩对河道行洪的影响。由于当时有限元计算模型还未成熟,多采用矩形网格和正交曲线网格模型开展研究。桥墩的形状与计算网格单元的形状并不十分吻合,因此,需要采取相应的概化。曹民雄等[7]建议采用桥墩的阻水面积换算成桥墩所在网格单元的迎流面积,然后计算网格单元的宽度,计算出网格单元需要修改的地形高程值。而杨斌等[8]建议根据桥墩所阻挡的流量值来设计同样阻挡流量的网格修正高程值,计算公式如 (4)所示。MIKE 21 FM具有自适应网格的功能,只需要根据桥墩的设计形状和尺寸,在计算网格划分时,在局部设计同样形状和尺寸的计算区域,并对桥墩所在的计算区域进行网格加密处理。在开展工程后工况计算时,直接修改桥墩计算区域的网格高程至设计高程,本文案例修改高程后模型计算网格地形插值图见图3。

式中:α为河底高程增加值,单位为m;b1和b2为沿河宽方向桥墩宽度和计算网格宽度,单位为m;h为水深,单位为m。
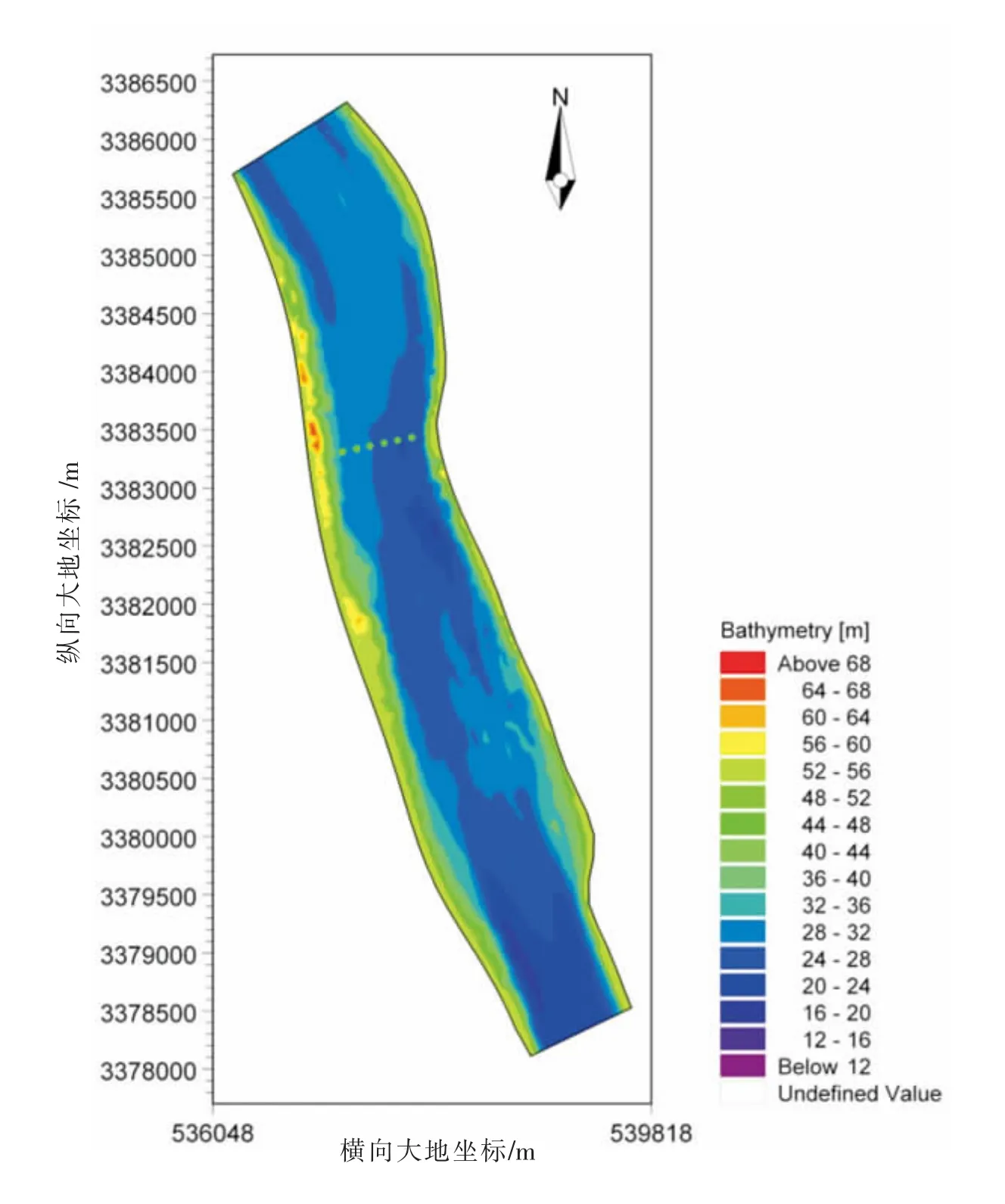
图3 桥墩所在计算区域高程修改后模型计算网格图Fig.3 Sketch of computing grid of river section with changed elevation
2.2 局部网格糙率修正法
对于不规则形的桥墩或者桥墩尺寸较小,为了保持数学模型的稳定性而无法进一步缩小模型计算网格的尺寸时,可采用局部网格糙率修正方法概化桥墩的影响。首先将桥墩看作栏污栅形式的阻水建筑物,桥墩局部阻力系数用式 (5)估算[7],然后将局部阻力系数转化为糙率的形式,用式 (6)计算:

式中:s为桥墩的宽度,单位为m;b为桥墩的间距,单位为m;θ为桥墩对水平方向的倾角,单位为°;β为桥墩的形状系数;H为平均水深,单位为m。
概化后桥墩区域所在网格的局部综合糙率系数为:

经过添加附加阻力后,模型计算区域的曼宁系数分布图见图4。

图4 桥墩所在计算区域曼宁系数分布图Fig.4 Chart of distribution of Manning coefficients of computing river section
2.3 局部网格高程修正+糙率修正法
针对大型桥梁工程,桥墩尺寸较大的情形,在水力学模型计算中采用局部网格高程修正和糙率修正相结合的方法,即将桥墩所在位置的计算网格地形高程修改至墩顶设计高程,同时把桥墩网格周边的相邻网格糙率适当增加,代表桥墩增加局部水流阻力。
3 计算结果与讨论
3.1 计算工况设计
本文所研究的宜昌江段洪水流量受到三峡水库的调节,面对三峡水库不同设计频率的入库流量,宜昌江段不同频率洪峰流量 (三峡出库流量)以及相应的洪水水位见表1。本研究以三峡工程对水库下游江段设计防洪标准百年一遇洪水为例,计算分析不同桥墩概化处理方法对洪水水位及行洪流速的影响。计算工况为4种,工况1:P=1%现状,即无桥墩工况,作为对照工况;工况2:P=1%高程修正,对桥墩处根据桥墩设计高程修改河道地形高程;工况3:P=1%糙率修正,按照阻水等价影响,对桥墩处糙率进行修正;工况4:P=1%高程修正+糙率修正。

表1 三峡水库设计洪水成果表Table 1 Result of design floods of Three Gorges Reservoir
3.2 计算结果与实测结果比较
为了验证所建立的数值模型的可靠性,本文采用2016年7月的长江洪水数据,将不同工况数学模型计算结果与现场实测数据进行了对比,桥墩上游断面和下游断面的对比结果见图5和图6。可以看出,糙率修正法计算结果较为平顺,但与实测结果的差别相对较大。而采用高程修正法和高程修正+糙率修正法计算结果与实测结果十分接近,但同时,高程修正法在桥墩附近的流速与实测值仍存在一定的差别。

图5 桥墩所在下游断面垂向流速计算值与实测值比较Fig.5 Comparison between calculated and measured values of vertical flow velocity at downstream section of the bridge pier
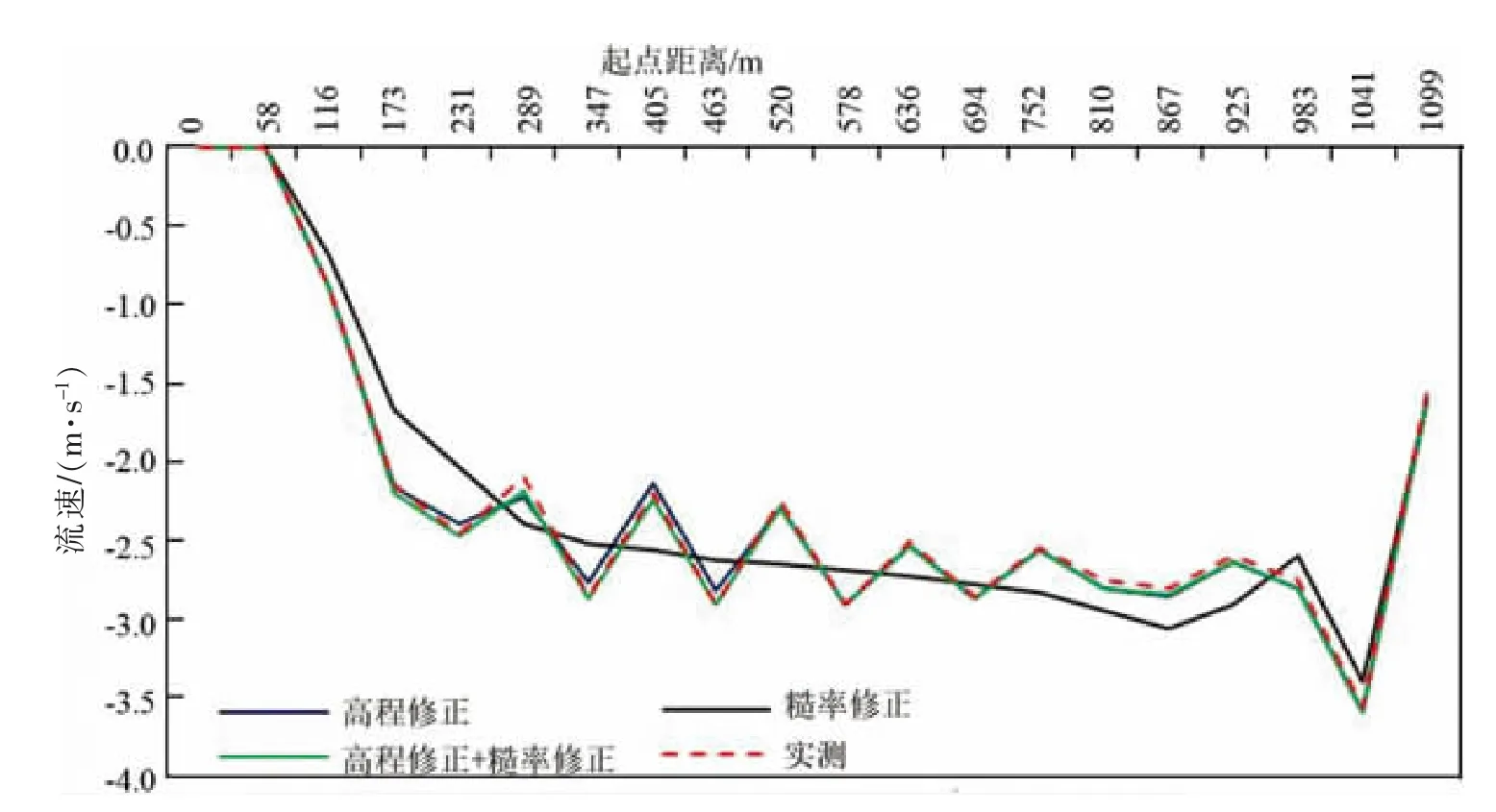
图6 桥墩所在上游断面垂向流速计算值与实测值比较Fig.6 Comparison between calculated and measured values of vertical flow velocity at upstream section of the bridge pier
3.3 壅水计算结果分析
平面二维水动力数学模型计算结果表明,百年一遇洪峰条件下 (55 000 m3·s-1),长江宜昌江段上游水位为53.1 m,下游为设计水位52.3 m,最大水深近30.0 m,水面坡降万分之0.7,工程前工况1水位等值线见图7(a)。由图可见,MIKE 21水动力 (FM)模块可较好地模拟洪水位的分布,在弯道处,由于水流惯性的影响,水位呈现出 “凹低凸高”的规律,最大横向水面坡降达万分之0.8。
工况2与工况1的水位差值分布见图7(b),可见,桥墩用修改地形高程的方式概化以后,整体上对桥梁上游河段的水位造成壅高影响,最大影响程度0.2~0.3 m,平均影响程度0.1 m左右,影响范围达2.5 km;对下游水位的影响局限于桥墩附近较小的范围,主要表现为水位降低,降低幅度为0.1 m左右,影响范围约50.0 m。工况3与工况1的水位差值分布见图7(c),也反映出桥墩用增加糙率的方式概化以后,对桥梁上游河段的水位造成壅高影响,影响程度仅有0.1 m,影响范围为2.5 km;对下游水位的影响局限于桥墩附近较小范围,水位降低0.1 cm左右,影响范围约50.0 m。工况4与工况1的水位差值分布见图7(d),所计算得出的影响结果基本为工况2和工况3的叠加,桥梁上游水位最大增加程度0.2~0.3 m,该程度的影响范围与工况2相比稍有扩大。
计算结果表明,采用修改地形高程和修改网格糙率的方法得出的计算结果差别较大,采用修改地形高程的方法能够比较准确地反映桥墩对河道行洪的影响,采用修改网格糙率的方法得出的影响结果偏小,不利于指导涉水工程的防洪管理。但从提高数学模型计算稳定性的角度,推荐使用修改地形高程同时增加局部网格糙率的方法。
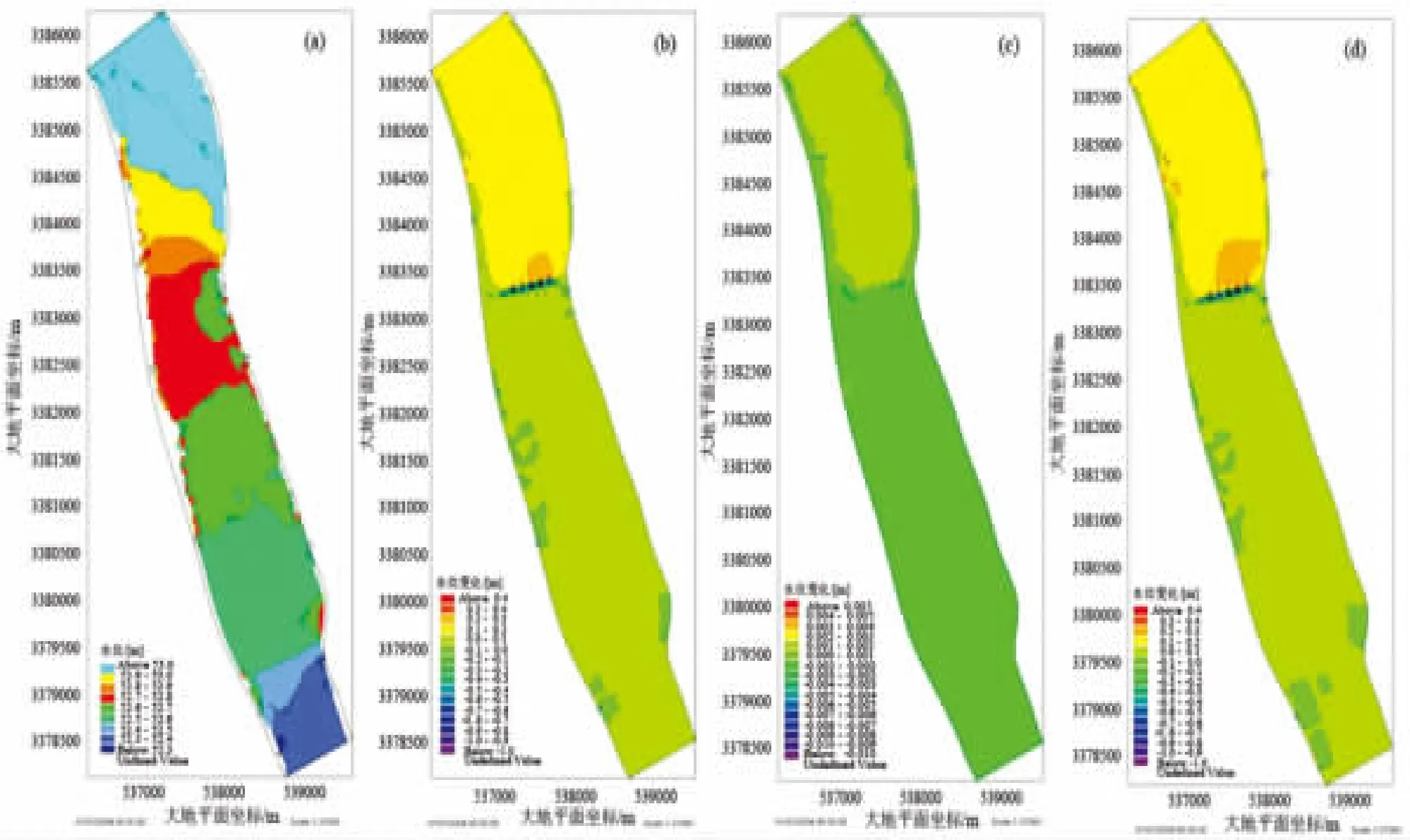
图7 工程前水位分布和工程后水位变化图Fig.7 Water level profile before construction and water level variation after construction of bridge
3.4 流速计算结果分析
平面二维水动力数学模型计算结果表明,百年一遇洪峰条件下 (55 000 m3·s-1),流速大小范围为0~4.95 m3·s-1,工程前流速分布见图8(a)。不同桥墩概化方法得出的流速影响结果见图8(b)-(d)。可以看出,几种不同的概化方法反映出的流速变化规律基本相似,桥墩上游流速减小,桥墩所在断面流速增加,受桥墩直接阻挡的下游河道流速减小,但两侧由于行洪流量增加流速增加。另外,与修改网格糙率方法得出的计算结果相比,采用修改桥墩处地形高程的方法概化桥墩,模型计算出桥墩对流速的影响程度和范围比较大,主要表现为桥墩上游流速减小,最大影响程度为-0.01 m3·s-1,平均影响程度为-0.02 m3·s-1;桥墩断面流速增加,平均增加程度为0.04 m3·s-1;受桥墩直接阻挡的下游河道流速减小,最大变化-0.1 m3·s-1,流速减小0.02 m3·s-1的影响范围达到3.9 km;桥墩两侧岸边流速增加,平均增加程度为0.04 m3·s-1,右边凸岸影响范围大,达到1.8 km,左边凹岸影响范围小,达到0.9 km。
采用修改计算网格糙率的方法概化桥墩,流速的变化程度较小,为0.001~0.002 m3·s-1,与实际情况的偏差较大,从流速变化的模拟精度考虑,同时考虑模型计算稳定的需要,推荐使用修改地形高程同时增加局部网格糙率的方法。
4 结论
采用平面二维数学模型评价桥梁工程对河流洪水位和行洪流速的影响是当前普遍采用的方法。但模型中对桥墩的不同处理方法,得出的评价结果会有差别。本文以长江宜昌江段区间某高速路桥为对象,采用修改网格地形高程、修改网格糙率和两者相结合三种方法模拟了桥墩对河道流速的影响,结果表明,修改地形高程方法模拟的结果与实际情况较为符合,对水位的影响达到了分米级,对流速的影响为厘米级,而采用修改网格糙率的方法得出的影响结果偏小,水位影响和流速影响为毫米级,不利于防洪安全。另外,考虑到数学模型计算稳定性的需要,同时考虑桥墩增加了河道局部阻力的实际情况,建议在开展数学模型计算时,采用修改网格地形高程和修改网格糙率相结合的方法。
[1]于海慧.“水深平均二维数学模型”在跨河桥梁防洪评价壅水计算中的应用[J].水利建设与管理,2014(2):29-32,48.
[2] 李磊,李月玉,孙艳,等.Hec-Ras软件在桥梁防洪评价中的应用[J].水力发电,2008,34(3):103-105.
[3]张细兵,余新明,金琨.桥渡壅水对河道水位流场影响二维数值模拟[J].人民长江,2003,34(4):23-24,40.
[4]陈绪坚,胡春宏.桥渡壅水平面二维数学模型模拟研究[J].中国水利水电科学研究院学报,2003,1(3):194-199.
[5]张小峰,白洋,王彩虹.桥墩附近水流结构的三维数值模拟[J].中国科技论文,2012,7(5):364-371.
[6]王晨阳,李孟国,李文丹.港珠澳大桥工程二维潮流教学模型研究[J].水道港口,2013,31(3):187-194.
[7]曹民雄,蔡国正,唐存本,等.崇海公路大桥潮流数值模拟计算与分析[C]//中国海洋工程学会.第十一届中国海岸工程学术讨论会暨2003年海峡两岸港口及海岸开发研讨会论文集.北京:海洋出版社,2003:126-133.
[8]杨斌,杨胜发.重庆地维长江大桥对长江行洪能力影响研究[J].重庆交通学院学报,2002,21(3):98-102.
The Influence of Pier Generalization Methods on the Simulation Results of Hydrodynamic Numerical Model
XIN Xiaokang
(Changjiang Water Resources Protection Institute,Wuhan 430051,China)
In order to identify the effects of different pier generalization methods used in two-dimensional mathematical model for flood control evaluation,three simplified methods of pier have been studied with the help of the MIKE 21 software and for the Yichang Yangtze River Bridge project under the hydrological conditions of 100-year flood.The simulation results showed nearly the same influence laws for the different pier methods.The water level increased while the velocity declined on the upstream.In contrast,both the water level and velocity at pier section increased simultaneously.The flow velocity decreased at the water blocking part downstream,while the flow velocity and the flow rate increased at unblocking parts on both sides of the river downstream.Nevertheless,the simulation results of mesh elevation correction method seems more reasonable,and taking into account of the model computational stability,the combination of mesh elevation correction and roughness correction is recommended in practice.
Hydrodynamic;numerical model;pier generalization methods;flood evaluation
TV13
A
2096-2347(2017)04-0034-08
10.19478/j.cnki.2096-2347.2017.04.05
2017-08-26
国家重点研发计划 (2016YFC0402204,2016YFC0402207)
辛小康 (1985-),男,湖北枝江人,博士,高级工程师,主要从事环境水力学和生态水力学研究。Email:xin.xiaokang@163.com
学术编辑:王 捷

