大坝监测数据多重共线性问题处理方法的比较研究

丁立，钱强强，赵俊，吴建晔

(湖州市测绘院，浙江 湖州 313000)

大坝监测数据多重共线性问题处理方法的比较研究

丁立*，钱强强，赵俊，吴建晔

(湖州市测绘院，浙江 湖州 313000)

多重共线性是大坝安全监测中一种常见的病态数据问题，为了削弱其对参数估计的影响，本文综合应用了主成分回归法、偏最小二乘回归法、岭回归法和Lasso法等四种有偏估计方法对大坝实测数据进行建模分析，并与多元线性回归模型结果进行比较。结果表明，多重共线性对模型的拟合及预报效果影响不大，但在模型的可解释性以及模型系数的稳定性方面，有偏估计方法更具优越性，且四种有偏估计方法针对多重共线性数据建模各有其特点。

多重共线性；主成分回归法；偏最小二乘回归法；岭回归法；Lasso法

1 引 言

多重共线性是指在自变量之间存在线性相关关系的现象，它的存在会影响最小二乘回归模型的参数估计，降低回归模型的可靠性，导致模型不能反映大坝的真实状态。为了削弱多重共线性对参数估计的影响，研究人员分别从子集选择、系数压缩以及变量重组等角度对参数估计方法进行了改进研究。其中子集选择法的代表方法主要是逐步回归法，而收缩法和降维法本质上都属于有偏估计方法，有偏估计方法在均方误差意义下对最小二乘估计具有改良作用，主要体现在参数估计值更为准确稳定[1～2]。经过长时间的不断开拓，以岭回归、偏最小二乘回归、主成分回归和Lasso法为代表的有偏估计法已被应用于不同研究领域。目前，处理大坝安全监测数据中多重共线性问题的有偏估计方法相对单一，大部分的研究主要考察单一方法的应用效果，对原理相近的几种方法的应用效果进行对比分析研究相对较少，因此，本文综合采用多种有偏估计方法建立大坝位移监控模型，通过实例比较各种方法的特点并分析其相对于最小二乘估计的优越性。

2 多重共线性及其处理方法

对于由单个因变量Y和n个自变量X1，X2，…，Xn构成的线性回归模型

Y=β1X1+β2X2+…+βnXn+ε

(1)

式中β1，β2，…，βn是未知参数，ε是随机误差项。

如果存在一组不全为0的常数α1，α2，…，αn使得式(2)成立

α1X1+α2X2+…+αnXn≈0

(2)

那么就称变量X1，X2，…，Xn之间存在多重共线性。

当变量间存在严重的多重共线性时，如果仍采用最小二乘法进行参数估计，可能引起法方程的解极不稳定，主要表现为，法方程中的系数或常数项存在舍入误差而产生微小变化时，会引起参数解的差异很大。

有偏估计能够有效地处理多元线性回归模型中的多重共线性问题。目前，处理多重共线性的常用方法有主成分回归法[3]、偏最小二乘回归法[4，5]、岭回归法和Lasso法[6]，表1中介绍了这四种方法的基本思想以及优缺点。四种方法的建模步骤及算法在其他相关文献中均有详细介绍，本文在此不再赘述。

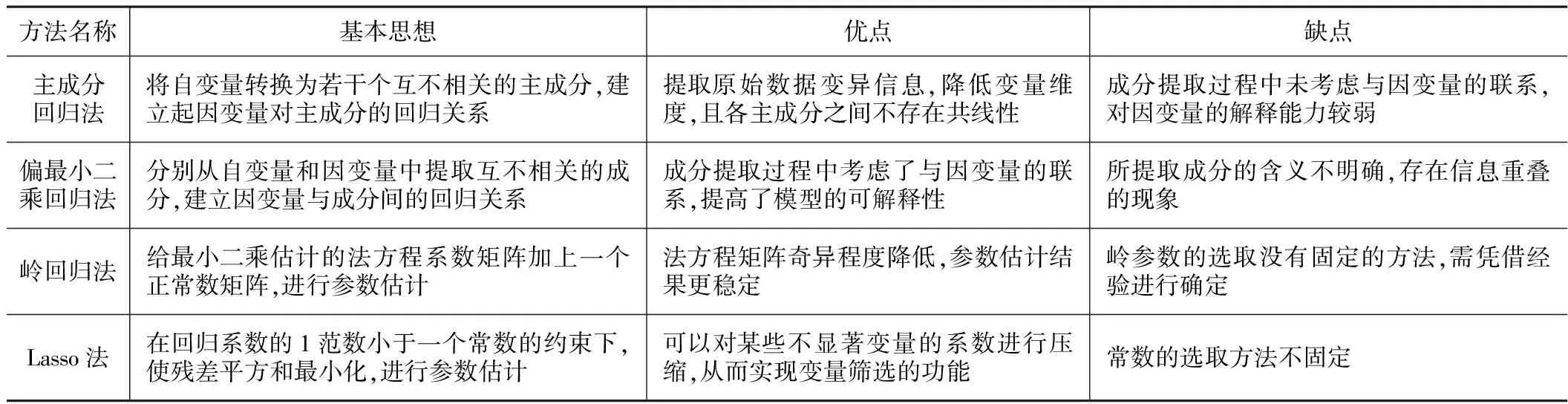
四种有偏估计方法的对比 表1

3 实例分析

为了说明在变量间存在严重多重共线性问题时最小二乘估计的不适用性以及比较四种有偏估计方法的效果，以某混凝土坝一坝段135期监测数据为例，分别建立位移监控模型。根据实测资料，确定大坝位移初选统计模型的表达式为：

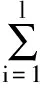
(3)

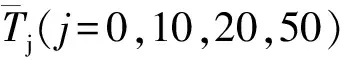
从135期大坝实测数据中取出前125期数据建立大坝位移y与水位因子、温度因子和时效因子之间的多元线性回归模型，按照逐步回归的步骤引进显著变量，剔除不显著变量，最终建立的模型为：

y=-353.6097H+1.3572H2-0.0017H3+0.0257T20

-0.1956T1s-0.0989T2s+0.0324T3s-1.0982θ

+0.2026lnθ+30698.8738

(4)

经计算，逐步回归模型的复相关系数为0.9848，F检验值为829.6，拟合残差平方和为0.272，如果取显著性水平α=0.05，该模型中所有的环境因子对位移y的影响都是显著的。

为了进一步验证逐步回归模型中系数的稳定性和可靠性，以下将对样本数据进行抽样，然后建立不同样本下对应的位移逐步回归模型，抽样的方案共分为5种：方案一，以135期观测数据为样本；方案二，隔一期数据抽取一个样本；方案三，隔两期数据抽取一个样本；方案四，隔三期数据抽取一个样本；方案五，隔四期数据抽取一个样本。五种抽样方案对应的逐步回归模型系数如表2所示。

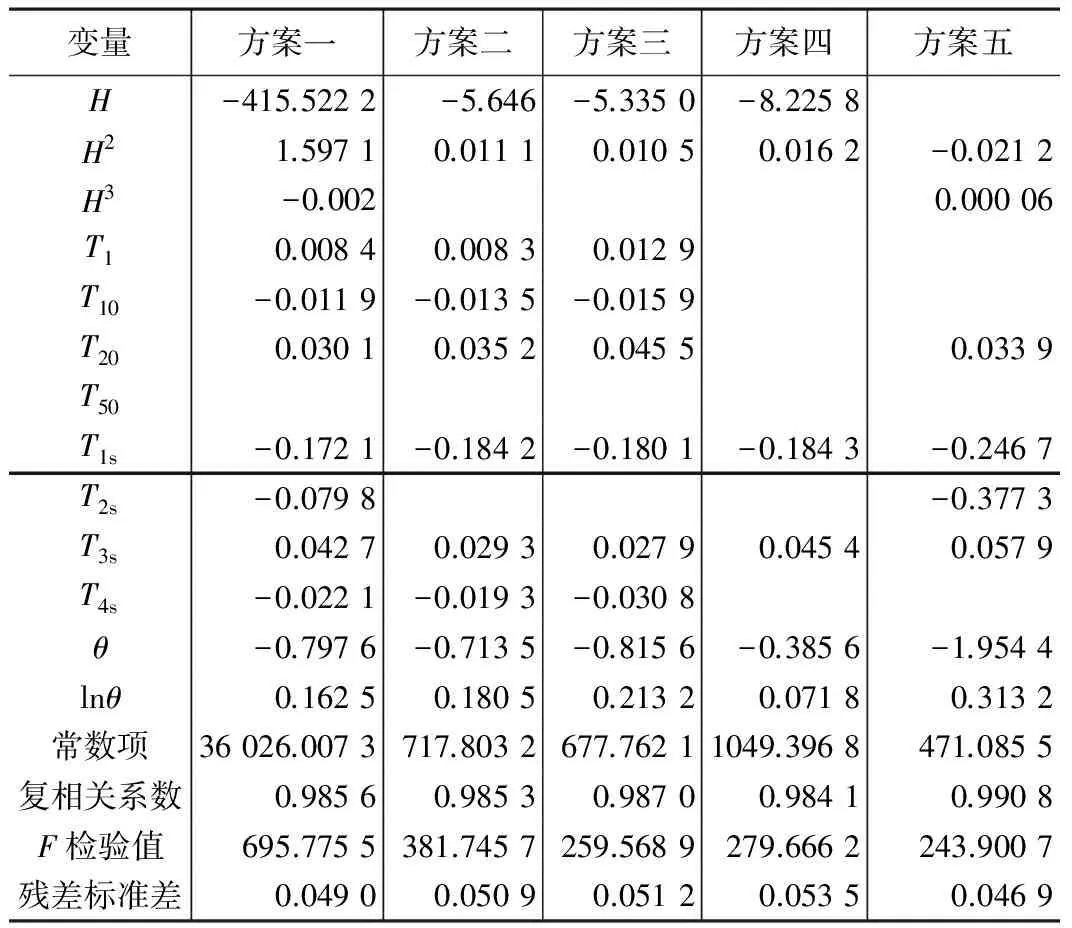
不同抽样方案对应的位移逐步回归模型系数 表2

同样采用大坝实测数据中前125期数据，分别采用四种有偏估计方法建立大坝位移回归模型。

在采用主成分回归法建模时，以主成分的累计贡献率达到95%为标准，共提取了3个主成分，各自的贡献率分别为61.51%、32.86%和1.97%，其累计贡献率达到96.34%，根据提取结果建立3个主成分对位移的回归模型：

y=0.04704H+9.086×10-5H2+2.339×10-7H3

+0.00241T1+5.587×10-4T10+0.00176T20

+0.00592T50-0.05639T1s+0.04222T2s

-0.00766T3s-0.00258T4s-0.01633θ

-0.03479lnθ-19.39277

(5)

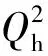
y=0.02981H+5.851×10-5H2+1.531×10-7H3

-0.00197T1-0.01094T10+0.01081T20

+0.01734T50-0.15491T1s+0.15429T2s

+0.00925T3s-0.00098T4s+0.04708θ

+0.03091lnθ-12.26631

(6)

在采用岭回归法建模时，选用L-曲线法确定岭参数，根据L-曲线法原理，当k=0.335时，可确定曲率最大点，因而k=0.335即为使用L-曲线法确定的岭参数，然后计算大坝位移岭回归模型为：

y=0.02729H+6.066×10-5H2+1.767×10-7H3

+0.00625T1-0.01657T10+0.02872T20

+0.01434T50-0.16295T1s+0.0954T2s

+0.00568T3s-0.01295T4s-0.36983θ

+0.13112lnθ-11.27464

(7)

在采用Lasso法建立大坝位移监控模型时，按照最小角回归算法(LARS)[7]求解Lasso问题，根据交叉检验法来确定惩罚参数t，当t=38.0166时，即算法进行到第18步时，CV=0.2965，取得最小值，其对应的估计参数即为选出的Lasso法最优解，因此Lasso法确定的大坝位移模型为：

y=0.04571H+9.38×10-5H2+0.00548T1

-0.01601T10+0.02549T20+0.01423T50

-0.15819T1s+0.1091T2s+0.00591T3s

-0.01181T4s-0.26741θ+0.10891lnθ

-15.42662

(8)

为了进一步比较各种方法所建大坝位移模型的预报效果，利用后10期数据进行预报，预报结果如表3所示。

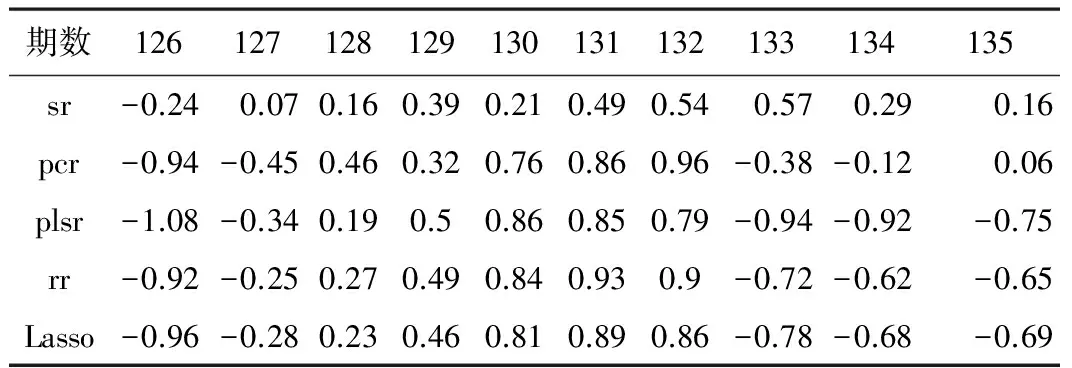
5种模型的预报结果(单位/mm) 表3

(注：sr：逐步回归模型，pcr：主成分回归模型，plsr：偏最小二乘回归模型，rr：岭回归模型)

通过以上的计算分析不难发现，无论是多元线性回归法，还是四种有偏估计方法，所建立的大坝位移监控模型都能达到令人满意的效果，而单从数值上看，多元线性回归法的拟合和预报效果更为理想。可见，仅将拟合及预报效果作为评价指标，多重共线性问题对最小二乘估计的影响微乎其微。

理论上，水位因子H2和H3都由H演变而来，三者的变化趋势是基本一致的，而且根据经验判断，大坝水平位移量应该与上游水位因子呈正相关关系，因此可以判定模型中三个因子的符号都应该为正，而在逐步回归模型中，尽管水位因子作为混凝土坝水平位移重要的影响因子都被选入最终的模型中，但三个水位因子的符号并不一致，其中位移量与水位因子H2呈正相关关系，而与H、H3却呈负相关关系，这显然给模型的解释带来了困难。不仅如此，表2也充分说明不同抽样方案对应的位移逐步回归模型系数的稳定性较差，在不同样本模型中同一变量对应的回归系数发生了较大的波动，有些因子甚至发生了符号上的变化，而且不同抽样方案选出的显著因子也有所差别。通过四种有偏估计方法建立的模型的可解释性则相对较好，水平位移量与上游水位因子均呈正相关关系，各个模型对应系数的数量级也趋于一致，且系数的符号和大小均未发生大的波动，较为稳定，不同抽样方案对应的各模型系数变化情况如图1～图4所示。

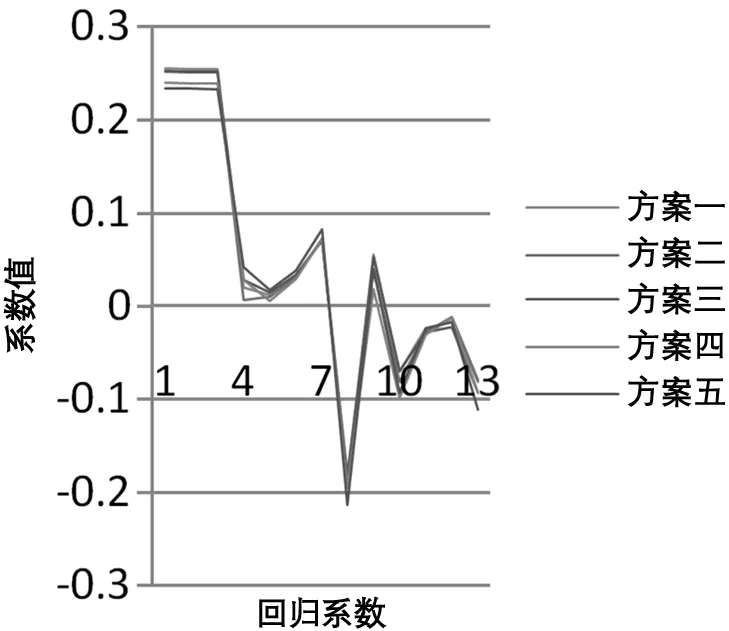
图1 主成分回归模型系数变化图

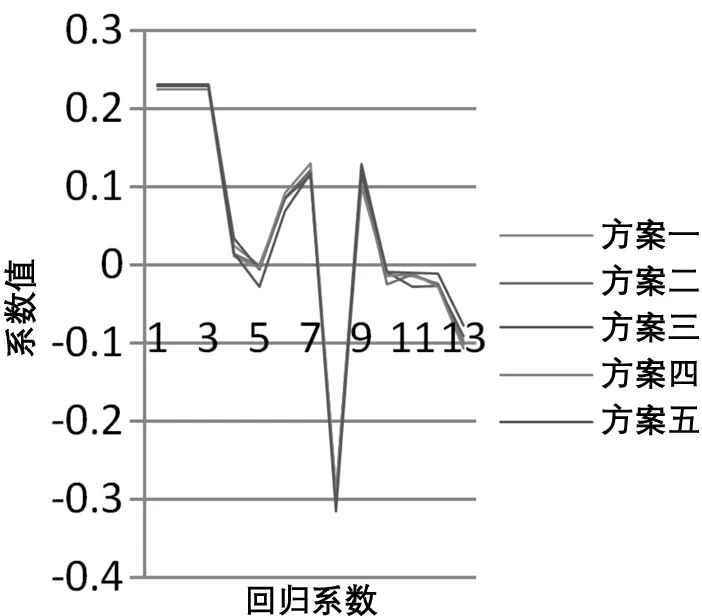
图2 偏最小二乘回归模型系数变化图

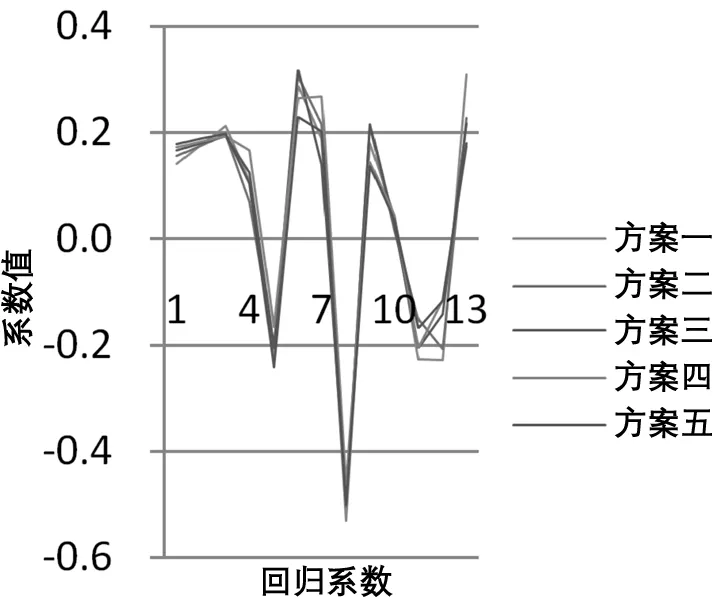
图3 岭回归模型系数变化图

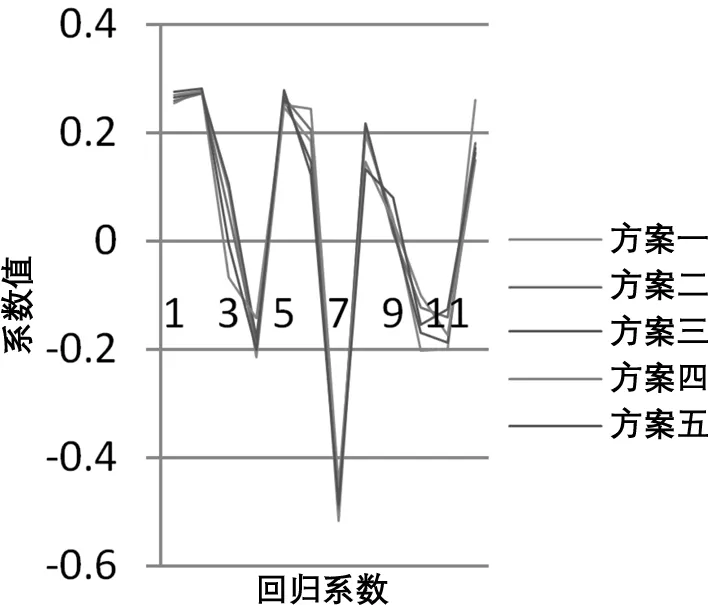
图4 Lasso模型系数变化图

通过图1～图4可以发现，主成分回归模型系数结构及变化趋势和偏最小二乘回归模型相似，岭回归模型系数结构及变化趋势与Lasso模型相似。

根据主成分回归法和偏最小二乘回归法的建模思想可以得知，两种方法都需要进行成分提取，所提取的成分之间线性无关，减弱了原始自变量间的多重共线性，最终利用所提取的成分进行回归处理。尽管两种方法的思想趋近，但建模原理有本质区别。从主成分回归法计算过程来看，三个主成分F1、F2和F3的累计贡献率达到96.34%，基本涵盖了自变量数据中绝大部分的变异信息，但由于在成分提取过程中，因变量并未发挥任何作用，所有主成分均是利用自变量相关系数矩阵求取的，因此不能保证各主成分对因变量拥有较强的解释能力。对于偏最小二乘回归法建模而言，成分的提取与自变量、因变量都息息相关，不仅要求携带尽可能多的原始自变量信息，而且要求每个成分与因变量的相关度尽可能大，该实例中当提取到第四个成分时，各成分对因变量的累计解释能力达到0.9721，所以偏最小二乘回归法提取成分的过程与主成分回归法相比更加合理完善。结合两者的拟合效果来看，主成分回归模型的拟合效果明显比偏最小二乘回归模型差，这很大程度上是由主成分对因变量解释能力不强导致的，从这一点上看，偏最小二乘模型的可解释性更强且可靠性更高。

岭回归法与Lasso法都涉及对系数的压缩，但两种方法对系数的压缩程度会存在差异，使用Lasso法建立的模型则会更加精炼、稀疏。从模型稀疏性的角度考虑，Lasso法能够降低模型的复杂度，显然更具优势，但也存在不可靠之处，如果惩罚参数选取不得当，会导致模型过于稀疏，一些重要的自变量可能未被选入模型中。在本实例中，岭回归法与Lasso法都能有效地处理大坝自变量因子间的多重共线性问题，虽然拟合效果比多元线性回归模型稍差，但所得的回归系数更符合实际，两种模型的系数结构及变化趋势较为吻合，对于不同样本方案的模型系数稳定性良好，而且在本实例中，使用Lasso法建立模型时，并未发生模型过于稀疏的情况，较岭回归模型而言，仅将水位因子H3的系数压缩为0，模型更加简洁。

4 结 语

本文以某混凝土大坝实测数据为例，分别采用多元线性回归法和四种有偏估计方法进行建模分析。本文的计算结果表明，受多重共线性的影响，多元线性回归法的处理结果在可解释性和系数的稳定性方面均比四种有偏估计方法要差。通过对基本原理相似的有偏估计方法比较可知，虽然主成分回归法和偏最小二乘回归法都能较有效地处理多重共线性问题，但偏最小二乘回归模型的可解释性更强且可靠性更高，采用岭回归法和Lasso法所建模型的系数结构及变化趋势较为吻合，而Lasso法建立的模型更加简洁稀疏。

[1] 唐小燕. 有偏估计若干问题的研究[D]. 哈尔滨：东北林业大学，2010.

[2] 归庆明，李国重，欧吉坤. 有偏估计与LS估计的比较与选择[J]. 测绘学报，2003，32(1)：26～30.

[3] 陈希孺，王松桂. 近代实用回归分析[M]. 广西人民出版社，1984.

[4] 付凌晖，王惠文. 多项式回归的建模方法比较研究[J]. 数理统计与管理，2004，23(1)：48～52.

[5] 王惠文，吴载斌，孟洁. 偏最小二乘回归的线性与非线性方法[M]. 国防工业出版社，2006.

[6] 张燕，宋俊峰，童行伟. 郑州白糖期货价格的模型选择方法[J]. 北京师范大学学报·自然科学版，2011，47(6)：551～557.

[7] 周玮. 变量选择中的LARS算法及其在国民经济中的应用[D]. 济南：山东大学，2011.

AComparativeStudyontheProcessingMethodsofMulticollinearityinDamMonitoringData

Ding Li，Qian Qiangqiang，Zhao Jun，Wu Jianye
(Huzhou Institute of Surveying and Mapping，Huzhou 313000，China)

Multicollinearity is a kind of common pathological data problem in dam safety monitoring，in order to weaken the influence on parameter estimation，principal component regression，partial least squares regression，ridge regression and lasso method are comprehensively applied to modeling analysis of dam observation data，and results are compared with multiple linear regression model’s. It shows that the multicollinearity has little effect on the model fitting and forecasting，but biased estimation methods have advantages in model interpretability and stability of model coefficients，and four kinds of biased estimation methods have their own characteristics for modeling with multicollinearity data.

multicollinearity；principal component regression；partial least squares regression；ridge regression；lasso method

1672-8262(2017)06-139-04

P207

B

2016—11—01

丁立(1989—)，男，硕士，助理工程师，主要从事安全监测数据处理相关工作。